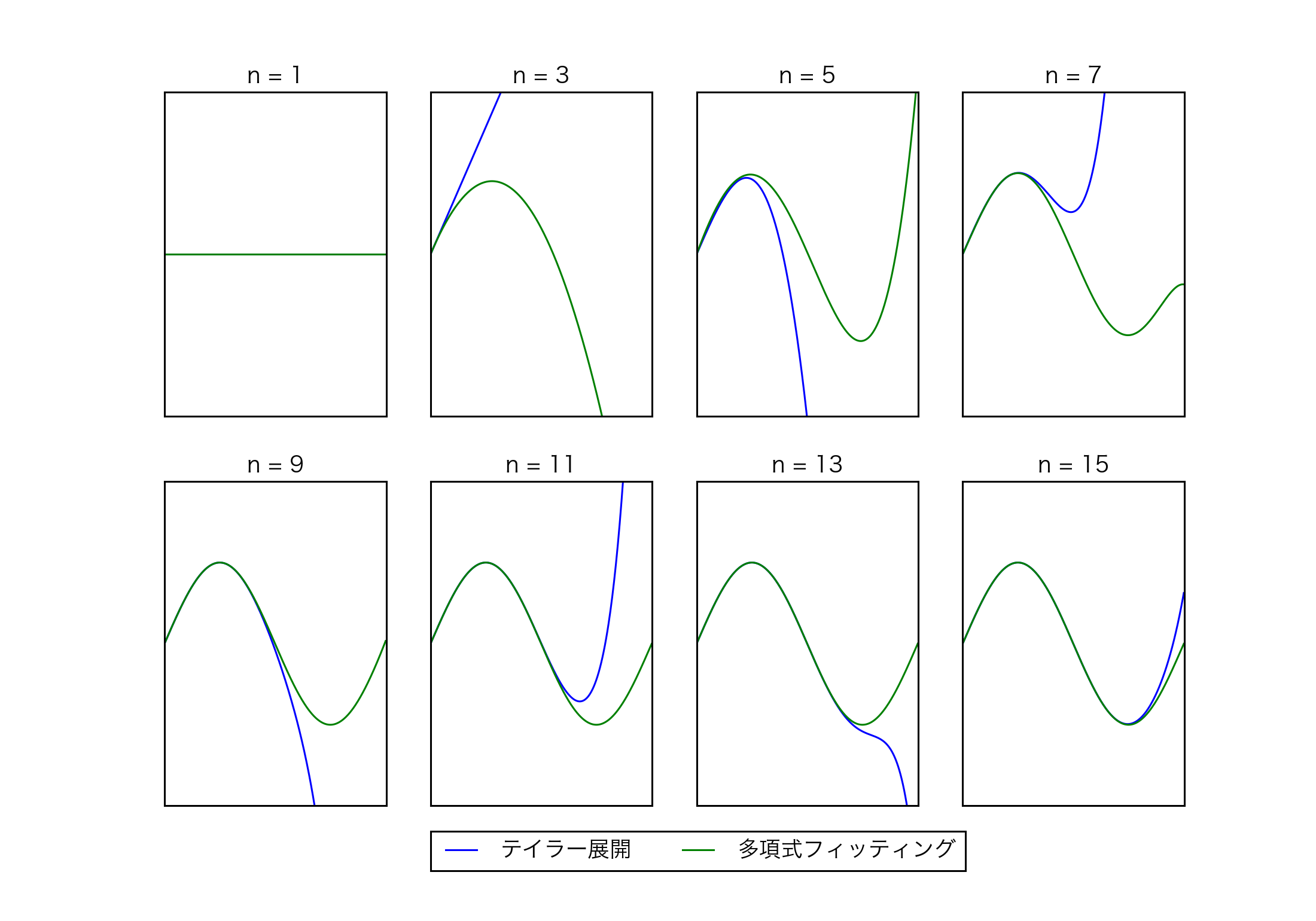
ある関数を機械学習するのに必要十分な訓練データセットは何かという問題があります。sin関数のようなテイラー展開できる関数を考えた場合に、$n$次のテイラー展開と同精度を得るには、$n$点の訓練データがあれば必要十分と言えたらきれいだなと思い実験してみました。
実際に試してみると、色々勘違いしていたことがわかりました。まずsin関数を近似しようとすると線形回帰では無理で、多項式フィッティングを行う必要があります。
$n$次のテイラー展開と同様にということで、$n$次までの多項式を基底関数とした$n$次元の特徴ベクトルで線形回帰を行うわけですが、$n$個の基底関数に対する重みを求めるには$n$個の訓練データがあれば良いという訳で、最初に考えたことは当たり前の結果でした。
また実際に試してみると$n$次のテイラー展開と多項式フィッティングの結果は一致せず、多項式フィッティングの方がずっと精度が良いようでした。これはテイラー展開の係数は$n\rightarrow\infty$の極限で適切な値となっているためではないかと思います。
上図は$n=1, 3, \dots ,15$でのsin関数のテイラー展開と多項式フィッティングの結果です。多項式フィッティングは与えられた次数の元で誤差が最小になるように係数を最適化しますから、テイラー展開より誤差が小さくなって当然かなと思います。
上図は$n=1, 3, \dots ,15$でのsin関数と、テイラー展開、多項式フィッティングによる近似の平均二乗誤差になります。多項式フィッティングの誤差が$n=15$で増えているのがちょっと気になりますが、多項式フィッティングの方がテイラー展開よりずっと誤差が少ないです。