PRML第9章の混合ガウス分布のためのEMアルゴリズムを実装した。Jupyter notebookへのリンク
結果
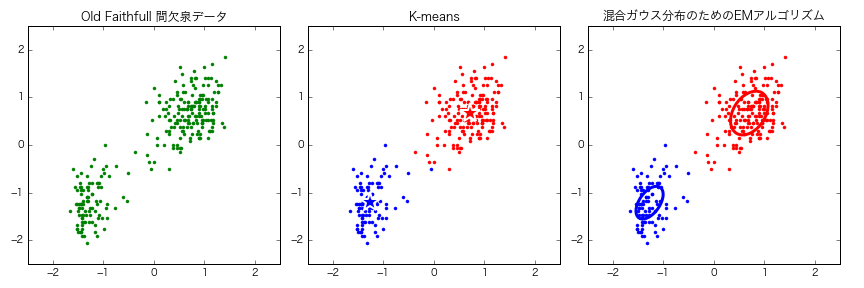
Old Faithful間欠泉データをK-meansと混合ガウス分布のためのEMアルゴリズムでクラスタリングした。
考察
混合ガウス分布のためのEMアルゴリズムは、混合ガウス分布以外のモデルを考えれば、様々な問題に応用できる。
混合ガウス分布のためのEMアルゴリズム
混合ガウス分布(Mixtures of Gaussians)
混合ガウス分布はK個のガウス分布の重ね合わせで表される。$$p(\mathbf{x}) = \Sigma_{k=1}^{K} \pi_{k} \mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})$$各ガウス分布$\mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})$は__混合要素(mixture compornent)と呼ばれ、それぞれ個別に平均$\mathbf{\mu{\rm{k}}}$、共分散$\mathbf{\Sigma{\rm{k}}}$のパラメータを持つ。
パラメータ$\pi_{k}$を__混合係数(mixing coefficient)と呼ぶ。$$\Sigma{k=1}^{K} \pi{k} = 1$$ $$0 \leqslant \pi_{k} \leqslant 1$$である。
潜在変数(latent variables)を導入
K次元の2値確率変数$\mathbf{z}$を導入する。$\mathbf{z}$は$\mathbf{x}$がどの混合要素から生じたかを表す。1-of-K符号化法をとる(どれか1つの$z_{k}$だけが1で、他は0)。$\mathbf{x}$と$\mathbf{z}$の同時分布$p(\mathbf{x}, \mathbf{z})$を以下のように表す。$$p(\mathbf{x}, \mathbf{z})=p(\mathbf{z})p(\mathbf{x}|\mathbf{z})$$$p(\mathbf{z})$は混合係数$\pi_{k}$で以下のように定まる。$$p(z_{k}=1)=\pi_{k}$$1-of-K符号化を用いるので、次のようにも書ける。$$p(\mathbf{z})=\Pi_{k=1}^{K}\pi_{k}^{z_k}$$$\mathbf{z}$の値が与えられたもとでの$\mathbf{x}$の条件付き分布は次のガウス分布である。$$p(\mathbf{x}|z_{k}=1)=\mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})$$これは$$p(\mathbf{x}|\mathbf{z})=\Pi_{k=1}^{K} \mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})^{z_{k}}$$という形にも書ける。$p(\mathbf{x}, \mathbf{z})$を周辺化して、先の$p(\mathbf{x})$を得る。$$p(\mathbf{x})=\Sigma_{\mathbf{z}}p(\mathbf{z})p(\mathbf{x}|\mathbf{z})=\Sigma_{k=1}^{K} \pi_{k} \mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})$$$\mathbf{z}$を導入しても意味がないように見えるが、EMアルゴリズムの導出で必要になる。
負担率(responsibility)
$\mathbf{x}$が与えられたもとでの$\mathbf{z}$の条件付き確率を$\gamma(z_{k})$で表す。
\begin{align}
\gamma(z_{k})\equiv p(z_{k}=1|\mathbf{x})&=\frac{p(z_{k}=1)p(\mathbf{x}|z_{k}=1)}{\Sigma_{j=1}^{K}p(z_{j}=1)p(\mathbf{x}|z_{j}=1}\\
&=\frac{\pi_{k}\mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})}{\Sigma_{j=1}^{K}\pi_{j}\mathcal{N}(\mathbf{x}|\mathbf{\mu_{\rm{j}}}, \mathbf{\Sigma_{\rm{j}}})}
\end{align}
$\pi_{k}$を$z_{k}=1$なる事象の__事前確率__、$\gamma(z_{k})$を$\mathbf{x}$を観測したときの対応する__事後確率__とみなす。$\gamma(z_{k})$は、混合要素kが$\mathbf{x}$の観測を「説明する」度合いを表す__負担率(responsibility)__としても解釈できる。
混合ガウス分布のためのEMアルゴリズム
- 平均$\mathbf{\mu_{\rm{k}}}$、分散$\Sigma_{k}$、混合係数$\pi_{k}$を初期化し、対数尤度の初期値を計算する。
- $\mathbf{E}$ステップ:現在のパラメータ値を使って、負担率を計算する。$$\gamma(z_{nk})=\frac{\pi_{k}\mathcal{N}(\mathbf{x_{\rm{n}}}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})}{\Sigma_{j=1}^{K}\pi_{j}\mathcal{N}(\mathbf{x_{\rm{n}}}|\mathbf{\mu_{\rm{j}}}, \mathbf{\Sigma_{\rm{j}}})}$$$\mathbf{x_{\rm{n}}}$はn番目のデータ点。$z_{nk}$はn番目のデータ点に対する潜在変数。
- $\mathbf{M}$ステップ:現在の負担率を使って、次式でパラメータ値を再計算する。
\begin{align}
\mathbf{\mu_{\rm{k}}^{\rm{new}}}&=\frac{1}{N_{k}}\Sigma_{n=1}^{N}\gamma(z_{nk})\mathbf{x_{\rm{n}}}\\
\Sigma_{k}^{new}&=\frac{1}{N_{k}}\Sigma_{n=1}^{N}\gamma(z_{nk})(\mathbf{x_{\rm{n}}}-\mathbf{\mu_{\rm{k}}^{\rm{new}}})(\mathbf{x_{\rm{n}}}-\mathbf{\mu_{\rm{k}}^{\rm{new}}})^{T}\\
\pi_{k}^{new}&=\frac{N_{k}}{N}
\end{align}
ただし$$N_{k}=\Sigma_{n=1}^{N}\gamma(z_{nk})$$
4. 対数尤度$$\ln(p(\mathbf{X}|\mathbf{\mu}, \mathbf{\Sigma}, \mathbf{\pi})=\Sigma_{n=1}^{N}\ln\{\Sigma_{k=1}^{K}\pi_{k}\mathcal{N}(\mathbf{x_{\rm{n}}}|\mathbf{\mu_{\rm{k}}}, \mathbf{\Sigma_{\rm{k}}})\}$$を計算し、パラメータ値の変化または対数尤度の変化を見て収束性を確認し、収束基準をみたしていなければステップ2に戻る。
参考
C.M.ビショップ著、元田浩・栗田多喜夫・樋口知之・松本裕治・村田昇監訳、パターン認識と機械学習、第9章、丸善出版