スパースモデリング第3章追跡アルゴリズムのアルゴリズムをPythonで実装.
コードと実験結果をまとめたJupyter notebook.
以下の貪欲法と凸緩和の手法を実装.IRLSはちょっと怪しい…
貪欲法
- 直交マッチング追跡(orthogonal matching pursuit; OMP)
- マッチング追跡(matching pursuit; MP)
- 弱マッチング追跡(weak matching pursuit; WMP)
- しきい値アルゴリズム
凸緩和の手法
- 反復再重み付け最小二乗法(iterative-reweighted-lease-sqaures; IRLS)
貪欲法の概要
初期化
$k=0$として
- 初期解 $\mathbf{x}^{0}=\mathbf{0}$
- 初期残差 $\mathbf{r}^{0}=\mathbf{b}$
- 解の初期サポート$S^{0}=\emptyset$
メインループ
$k \leftarrow k+1$として以下のステップを実行する.
- 誤差の計算,サポートの更新:$\mathbf{A}$の中から一番残差$\mathbf{r}^{k}$を減らせる列$\mathbf{a}_{j}$を$S^k$に追加
- 暫定界の更新:$\| \mathbf{Ax}-\mathbf{b}\|^{2}_{2} , \rm{subject} , \rm{to} , \rm{Support}\{\mathbf{x}\}=S^{k}$の最適解を$\mathbf{x}^{k}$とする.
- 残差の更新:$\mathbf{r}^{k}=\mathbf{b}-\mathbf{Ax}^{k}$を計算する.
- 停止条件:もし$\|\mathbf{r}^{k}\|<\epsilon_{0}$なら終了し,そうでなければ反復する.
誤差の計算,サポートの更新では$\mathbf{A}$の全ての列$\mathbf{a}_{j}$と残差$\mathbf{r}$の内積を計算し,内積の絶対値が最大となる列をサポートに追加する.つまり$\mathbf{r}$に平行な列を順番に追加していく.
貪欲法のアルゴリズムの違い
- OMP
- 上のまま
- MP
- $\mathbf{A}$ではなく新たにサポートに追加した$\mathbf{a}_j$のみで暫定解を更新
- WMP
- スカラー$t , (0<t<1)$をハイパーパラメータに追加
- 誤差の計算とサポートの更新で$\mathbf{r}^{k-1}$との内積の絶対値が$t\|\mathbf{r}^{k-1}\|$以上の$\mathbf{a}_j$が見つかったら計算を打ち切る.後はMPと同じ.
- しきい値アルゴリズム
- サポートに含まれる基底関数の個数$k$をハイパーパラメータに追加
- $\mathbf{b}$との内積の絶対値の大きい$\mathbf{a}_j$の上から$k$個をサポートとしてしまう.後は最小二乗問題を解き$\mathbf{x}$とする.
IRLSの概要
- $\left( P_{0} \right)$問題ではなく$\left( P_{1} \right)$問題を解く.
- 重み付き$L_{2}$ノルムで$L_{1}$ノルムを近似して$\left( P_{1} \right)$問題を解く.
- スパースな解を得るためにはむっちゃ反復する必要がある.
初期化
$k=0$として
- 初期近似解 $\mathbf{x}^{0}=\mathbf{1}$(全部1のベクトル)
- 初期重み行列 $\mathbf{X}^{0}=\mathbf{I}$
メインループ
$k \leftarrow k+1$として以下のステップを実行する.
- 最小二乗法:線形連立方程式$$\mathbf{x}_{k} = \mathbf{X}_{k-1}^{2} \mathbf{A}^{T} ( \mathbf{A} \mathbf{X}_{k-1}^{2} \mathbf{A}^{T} )^{+} \mathbf{b}$$を直接または反復法を用いて解き,近似解$\mathbf{x}_k$を得る.
- 重みの更新:$X_{k}(j,j)=|x_{k}(j)|^{0.5}$として重み対角行列$\mathbf{X}$を更新
- 停止条件:もし$\|\mathbf{x}_{k}-\mathbf{x}_{k-1}\|_{2}$が事前に与えられたしきい値より小さければ終了し,そうでなければ反復する.
実験
シミュレーション
$\mathbf{x}$ 50次元のベクトル
$\mathbf{b}$ 30次元のベクトル
$\mathbf{A}$ 30×50次元の行列,$[-1, 1)$の一様乱数を列正規化
- $\mathbf{x}$の非ゼロの要素数$k$として、その非ゼロ要素の値を$[-2, -1] \cup [1, 2]$の範囲の一様分布からiid抽出する.
- $k=1,...,10$で各200回シミュレーション
指標
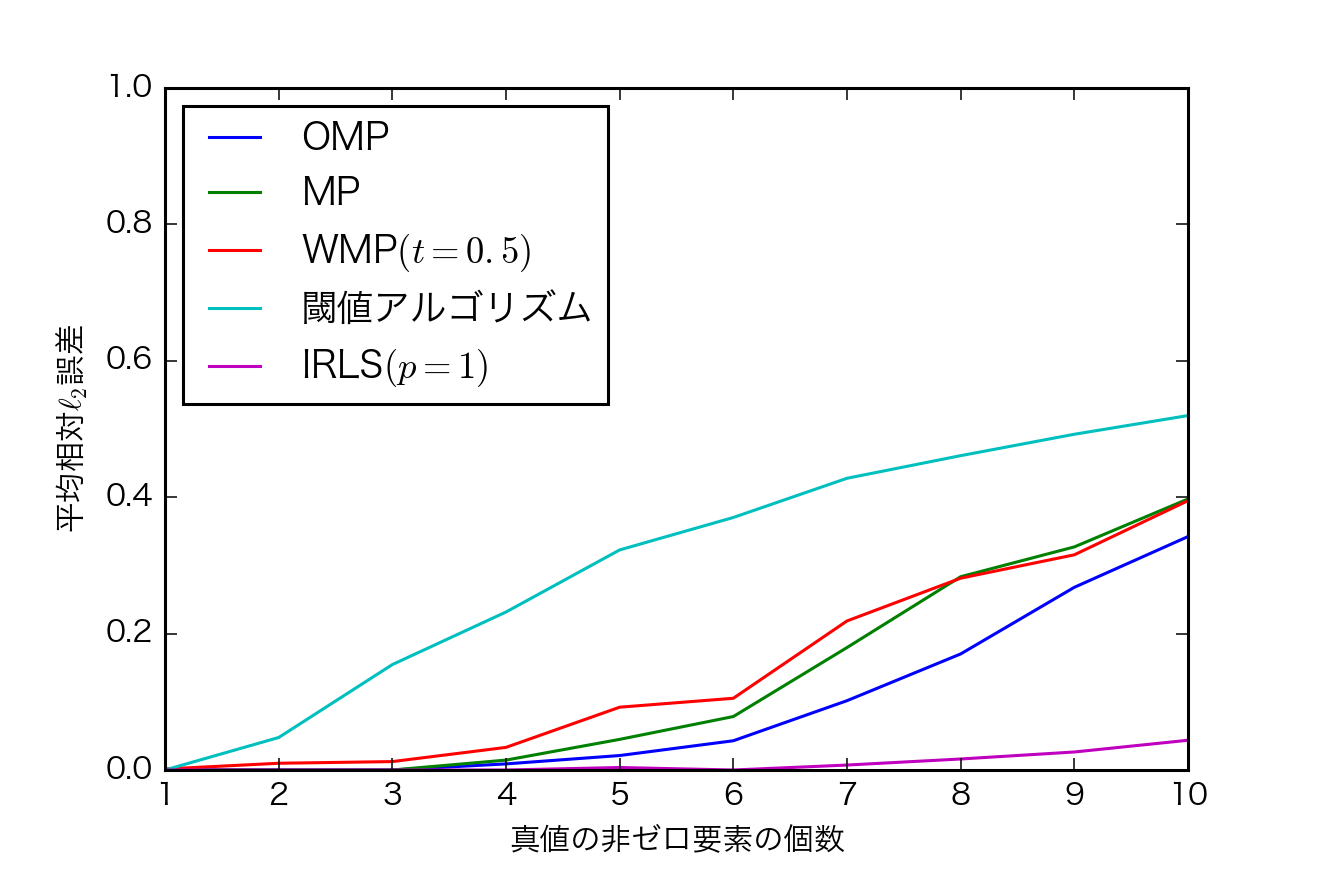
- 推定した$\mathbf{\hat{x}}$と真の$\mathbf{x}$の$L_2$ノルム
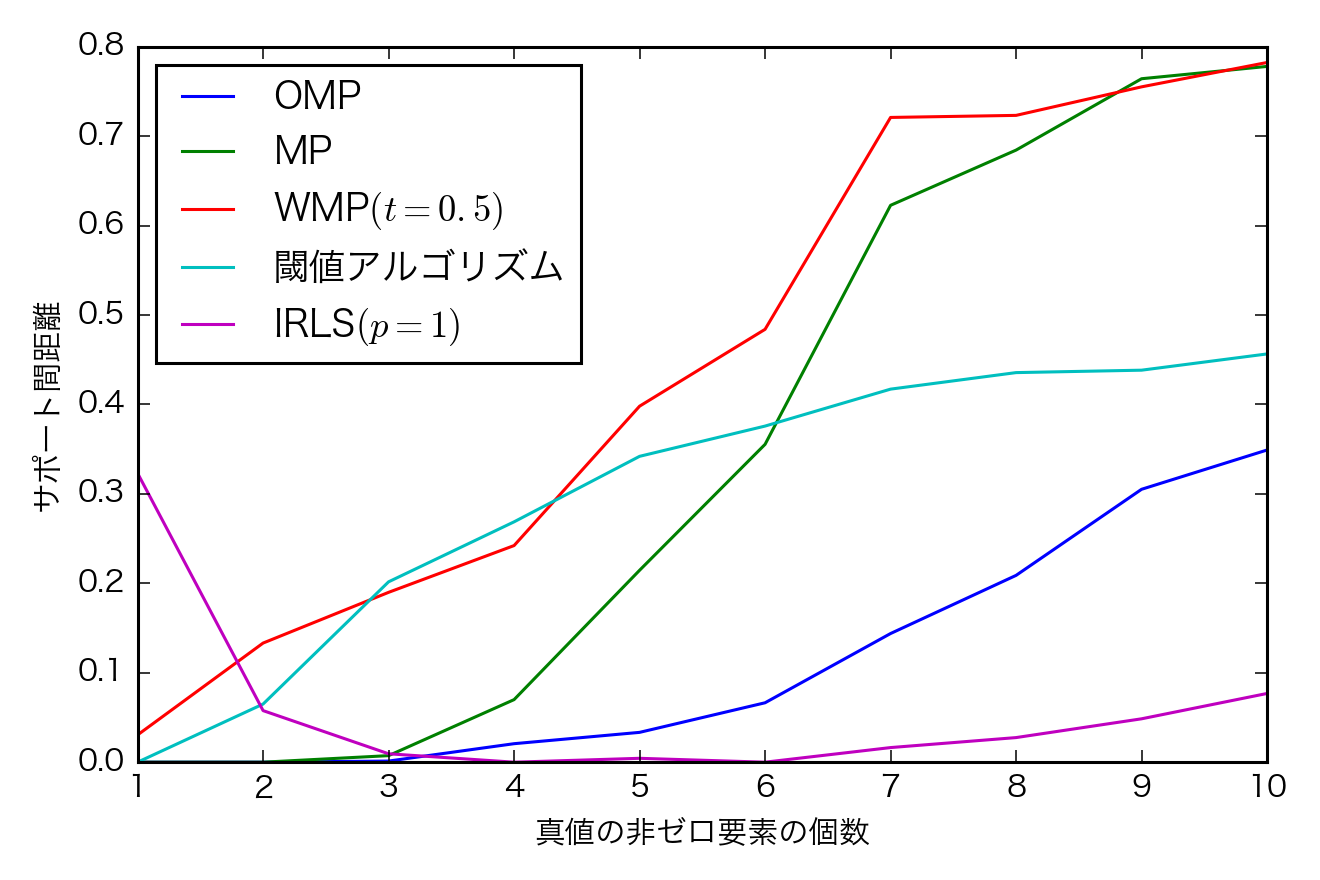
- 推定した$\mathbf{\hat{x}}$と真の$\mathbf{x}$のサポート間距離$$dist(\hat{S},S)=\frac{max\{|\hat{S}|, |S| \} - |\hat{S}\cap S|}{max\{|\hat{S}|,|S|\}}$$
- 200回のシミュレーションの平均をとる.
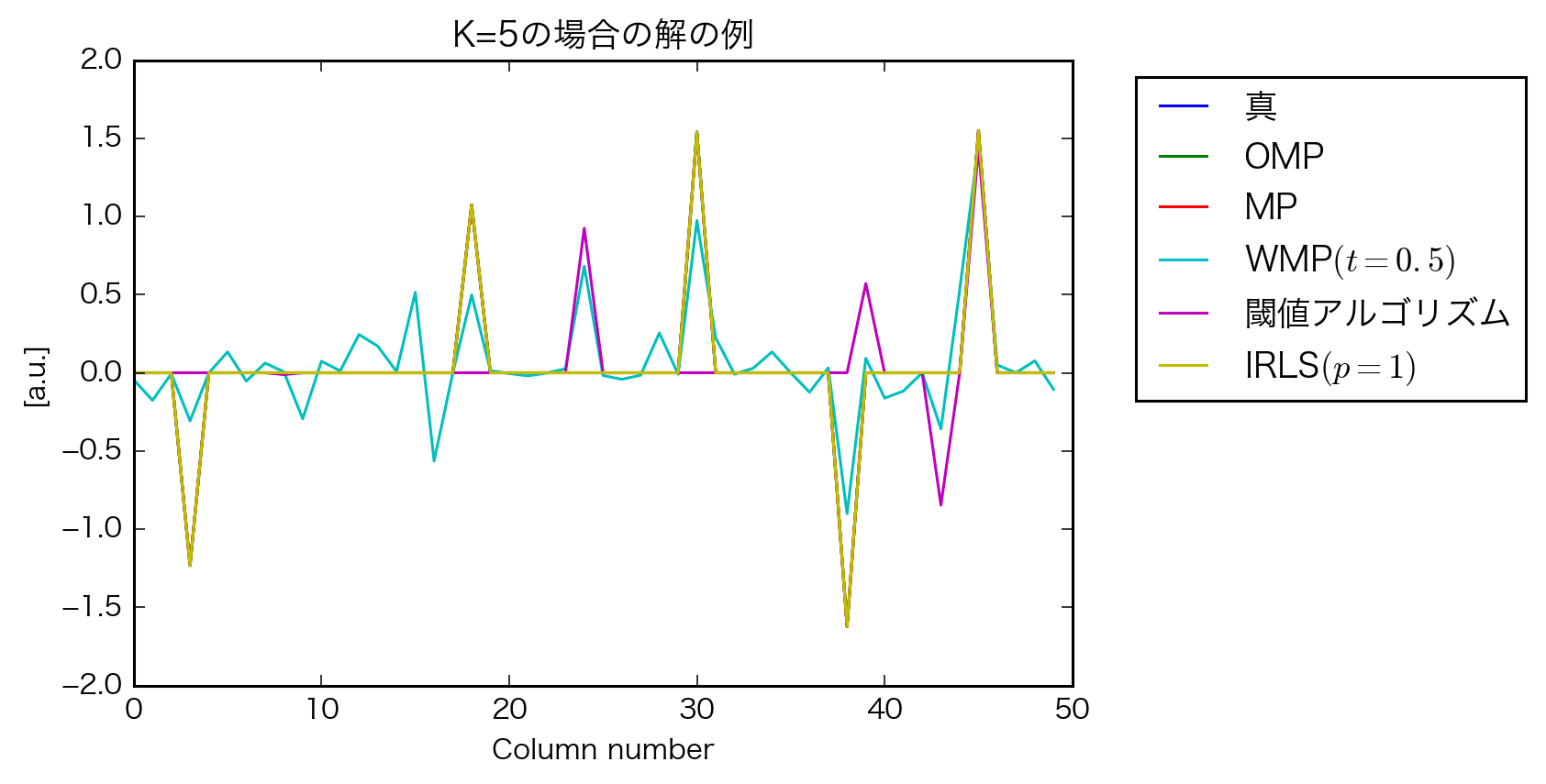
結果
- kが大きくなると誤差が増える.
- IRLSの誤差が小さいけども$L_{2}$誤差だから当然か
- OMPも結構頑張ってる.速いし
- kが低いときのIRLSのサポート間距離が大きくなってしまった.教科書ではそんなことは無いので反復が足りないか、不具合かも
- OMPもがんばってる.
考察
- OMP結構頑張ってる
- IRLSは教科書と結果が一致しないので原因の検討が必要