Michael Elad著、玉木徹訳のスパースモデリングの第2章3節のグラスマン行列の構築をPythonでやってみました。
スパースモデリングでは
$$(P_0): \min_x ||\mathbf{x}||_0 , \rm{subject , to} , \mathbf{b}=\mathbf{Ax}$$
という問題を解きます。$\mathbf{A}$は$n×m$の行列$(m>n)$とします。
ここで$\mathbf{A}$が直交行列に近い程($\mathbf{A}^T\mathbf{A}$が$\mathbf{I}$に近い程)$P_0$の解を得ることが容易になります。
$\mathbf{A}$は正方行列ではないので$\mathbf{A}^T\mathbf{A}$の非対角要素が全て0になることはなく、その下限は
$$\mu(\mathbf{A}) \geq \sqrt{\frac{m-n}{n(m-1)}}$$
となります。この$\mu(\mathbf{A})$を行列$\mathbf{A}$の__相互コヒーレンス__と呼びます。
何らかのアルゴリズムで$P_0$の解の候補$\mathbf{x}$を求めたときに$\mathbf{x}$が
$$ ||\mathbf{x}||_0 < \frac{1}{2}(1+\frac{1}{\mu(\mathbf{A})})$$
の条件を満たす場合、$\mathbf{x}$が$\mathbf{b}=\mathbf{Ax}$の制約の元で最もスパースな唯一の解であると言うことが出来ます(定理2.5)。つまり何らかの近似的なアルゴリズムで$\mathbf{b}=\mathbf{Ax}$を満たすスパースな$\mathbf{x}$を探していた場合に$\mu(\mathbf{A})$の値が小さい程、緩い基準で答えが見つかりやすいと言うことが出来ます。
と言う訳で$\mathbf{A}$の相互コヒーレンスが低い程うれしい訳ですが、
$$\mu(\mathbf{A}) = \sqrt{\frac{m-n}{n(m-1)}}$$
と相互コヒーレンスが下限に一致するような行列をグラスマン行列と言います。グラスマン行列は出来るだけ直交行列に近い$n×m$行列であると言うことが出来ます。
このようなグラスマン行列が構築できると$P_0$問題を解くのに何かと便利そうだなと言う気がする訳ですがスパースモデリングの「2.3 グラスマン行列の構築」に数値的にグラスマン行列を計算するMATLABコードが載っていたので、それをPythonに移植してみました(前置きが長い)。
アルゴリズム自体はグラム行列$\mathbf{G}=\mathbf{A}^T\mathbf{A}$の大きい値をシュリンクした後、SVD変換して行列のランクがNになるように処理する、を反復すると非対角成分の値が下限に近いグラム行列$\mathbf{G}$が得られ、最後にまたSVD変換で反復処理したグラム行列$\mathbf{G}$からグラスマン行列となった$\hat{\mathbf{A}}$を得るというものです。
グラスマン行列を構築するPythonコードは以下のGithubのipynbを参照。
https://github.com/kibo35/sparse-modeling/blob/master/ch02.ipynb
最後にグラスマン行列になった$\hat{\mathbf{A}}$を得る所は怪しいですがグラム行列への処理は教科書と同じ結果が得られていると思います。
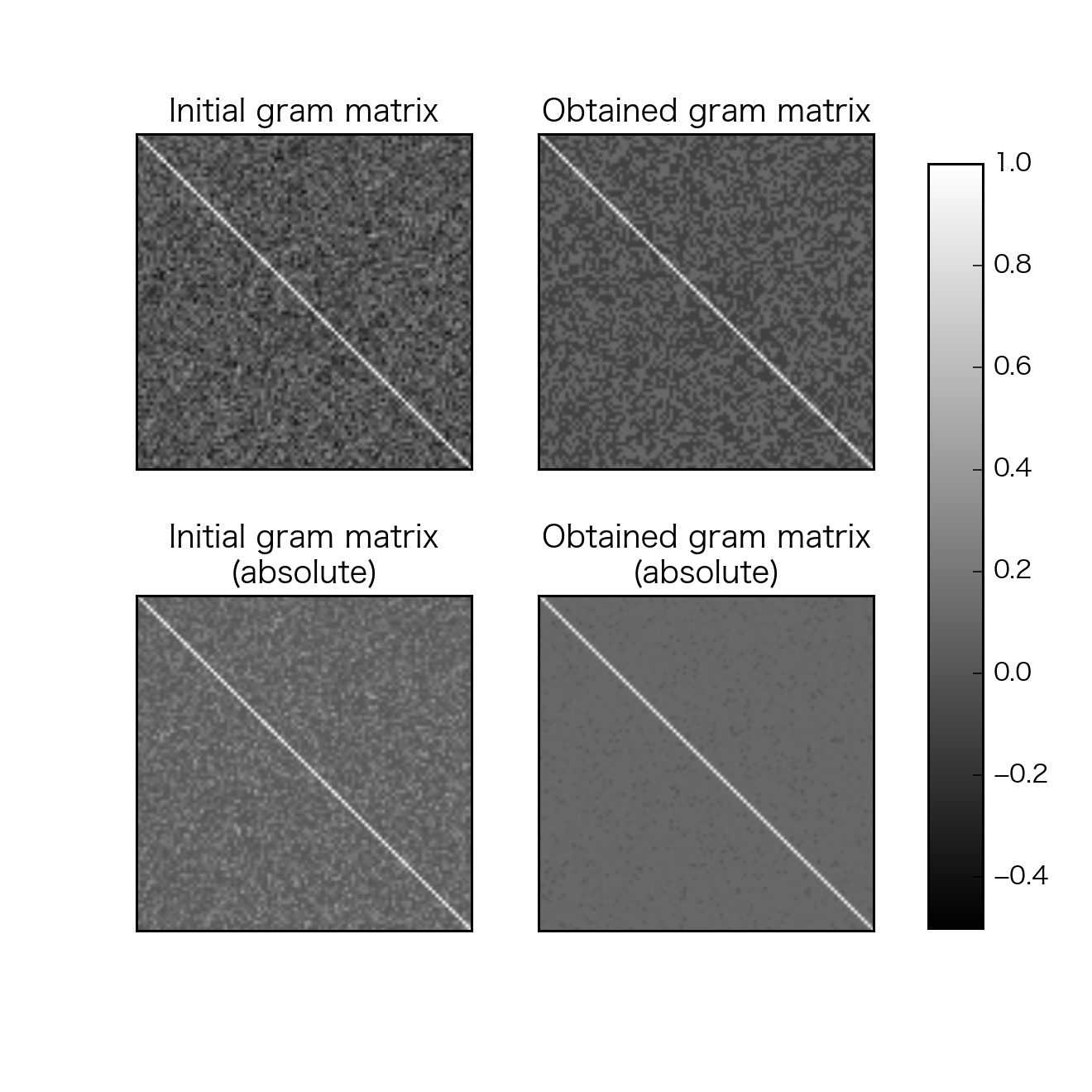
左上は正規分布で与えた冗長なシステム行列$\mathbf{A}$(50行×100列)のグラム行列$\mathbf{G}=\mathbf{A}^T\mathbf{A}$になります。右上は10000反復後のグラム行列になります。
下段の絶対値をとった画像を見ると非対角成分の値が一様になっていることがわかります。
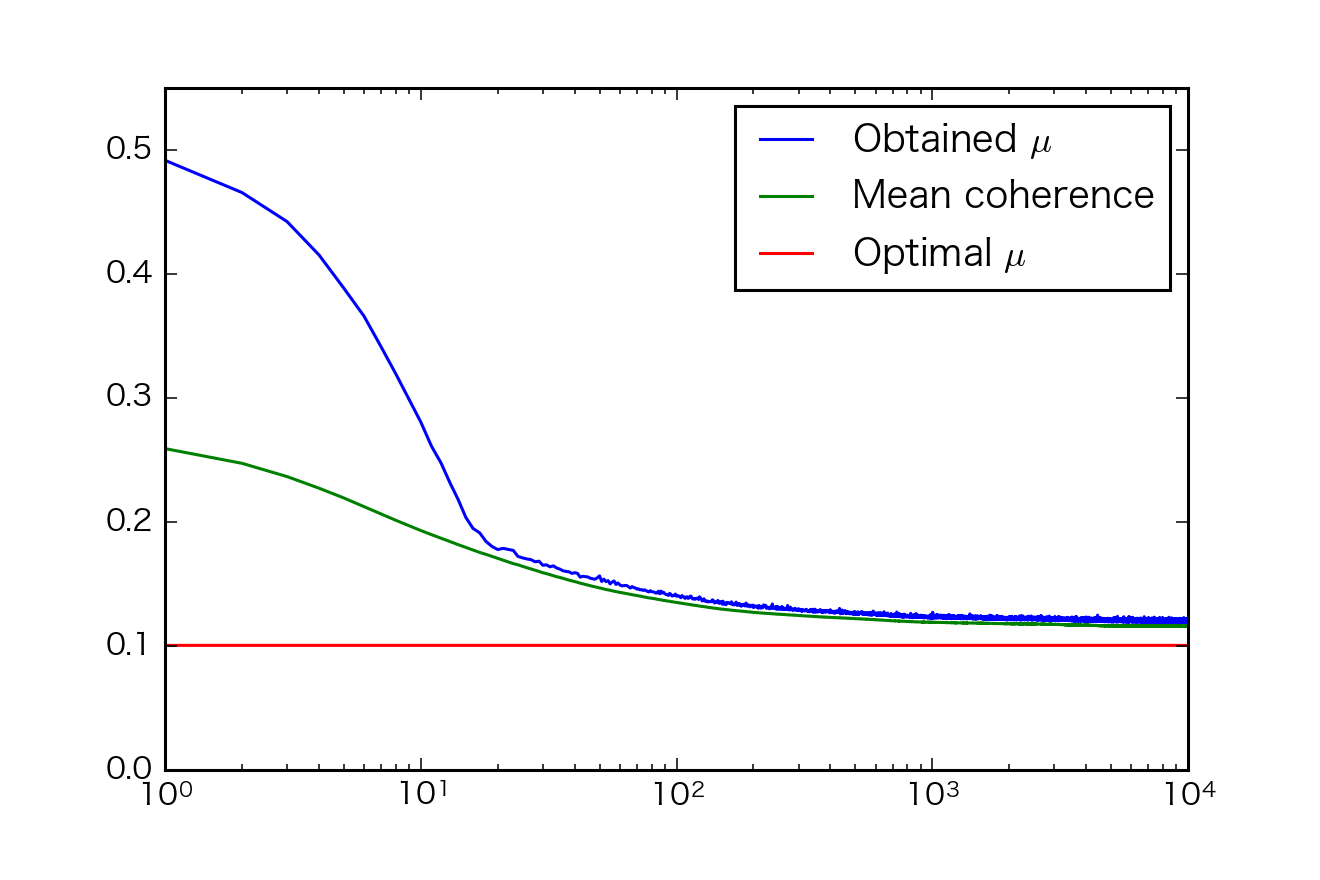
上の図は各反復におけるグラム行列の非対角成分の値をプロットしたものです。
とにかくスパースモデリングの第2章からわかることは、冗長なシステム行列$\mathbf{A}$の相互コヒーレンス$\mu(\mathbf{A})$(グラム行列の非対角成分の絶対値の最大値)の値がわかっており、その値から求まるある閾値より$L_0$ノルムが小さい解$\mathbf{x}$を見つけることが出来れば、それが一意な解と言うことが出来るので、がんばって$P_0$問題を解いてみようということです。