※自分の学習整理用として作成しています。
※なんとなくの理解を目指しているので、難しいことや細かいことは省いています。
実験計画法
品質を維持しつつ効率的にテストを実施するための方法論のこと。
簡単に言うと、少ない試験回数で高精度の結果情報を効率よく得よう、というもの。
適用できるできない場合もあるし、色々な都合で数をこなさなければいけない場合もあるので、使う使わないの判断(使える使えないの確認)は必要。
また、実験計画法と言っても手法はたくさんあって・・・
- 2水準要因計画
- 3水準要因計画
- 中心複合計画
- プラケットバーマン計画
- ボックスベンゲン計画
- 直交表
- ランダム
・
・
・
今回は直交表についてまとめます。
直交表とは
全ての因子から任意の2つを取り出して、そこでパターンが網羅できていればOK、というものです。
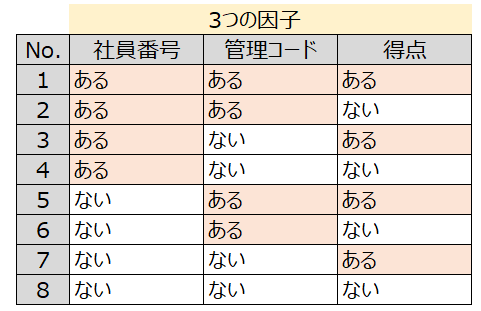
例えば、3因子2水準の場合
- 3因子・・・社員番号、管理コード、得点
- 2水準・・・因子の選択肢が2つ(今回は”ある””ない”の2つにしています)
パターンを網羅させようとすると、2×2×2=8パターンになる
(今回は触れませんが、たぶんこれが2水準要因計画なんだと・・・)
ここで登場するのが・・・
L4直交表
任意の2つの因子のパターンが網羅されていればOK、というのは以下の状態
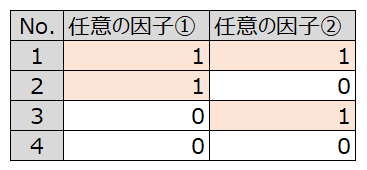
つまり、社員番号・管理コード、社員番号・得点、管理コード・得点で見た時に、それぞれでパターン網羅されていればOK、ということ。
それを踏まえてL4直交表を作成すると、こんな感じになります。
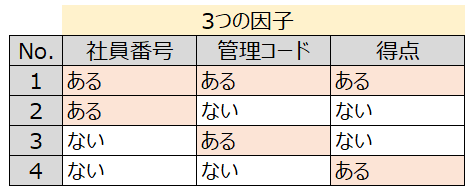
え、網羅しているやつから直交表にはめるのに時間かかるじゃん、と思いましたが
型は色々と用意されているので、簡単にできそう。
2水準用だと、L4、L8、L12・・・など
3水準用だと、L9、L27だったり、2水準と3水準の混合系とかもあるみたいです。
L9直交表だと、もともと4因子3水準で3×3×3×3=81パターンあるものを9パターンにできるので工数はかなり削減できそう。
一方で、L4直交表を例にすると、”ない””ない””ない”パターンが無かったりするので、落とせないパターンは追加でやる必要があったり、そこの判断は必要ですね。
さいごに
知っていると知っていないでは選択肢の数が変わってくるので、こういうのどんどん吸収していきたいです。
また、出ているものを評価するだけじゃなく、出ていないものが何か、本当にこれでいいんだっけ、を考えられる力をもっとつけたいなと改めて感じました!