はじめに
本投稿は、Schooの2016年末特別企画「Schoo advent calendar 2016」の8日目の記事になります。
皆さん初めまして。
株式会社Schooでデータサイエンティストをさせて頂いてます日高です。
Qiitaに初めて投稿、かつデータサイエンスに関することをということでどんなことを書けばいいか迷いました。
悩んだ挙句、自分が昔に書いた記事の焼き直しを投稿いたします。
元記事があるから楽だろうと思って書き始めたのですが、話の展開がうまくなかったり論理展開が間違っているところを直して書いたら結構大変なことになってしまい、冷汗かいてしまいました。
特に間違っていたところの証明のやり直しに思いのほか時間がかかってしまい、締め切りに間に合うかドキドキでした。
テーマは「相加平均と最小二乗法について」です。
いま流行りの話ではありませんが、理解が深まる一助となれば幸いです。
データブームのご時世に思うこと
「データ分析!解析!マイニング!」という言葉が今とてもブームですね。
世の中にはいろんなツールが出てきてやれることも広がって、専門知識がなくても使い方さえ分かれば組み上げることができ結果が出せる。
すごい時代になったなぁ・・・。
そう思います。
しかし。
- すぐにいろいろ試せて結果が出せるけど、その意味ってわかって使えているのだろうか?
- 使い方をたくさん知ってる、触っていることが重要視されて、意味や論理や使い道って軽視されてないだろうか?
- 手法を盲信していないだろうか?
- そこから出てきた結果って、どれだけ論理的に意味があるものなんだろう?
そんなことを思うことが増えてきました。
私は、世にたくさんのツールがあって誰でも楽に扱えるからこそ、データサイエンティストには専門の深い知識と考察力が必要とされるんだと思っています。
自分自身への自戒として
「その手法、使い方あってる?」
と問いかけながら、データと向き合う日々を過ごしております。
今回は平均の話
データを扱うときに必ずと言っていいほど計算する**「平均値」。
今回は皆さん誰でも計算したことがあるだろう「平均」の話を書きます。
平均の意味ってなかなか考える機会はないだろうと思いますし、そこから、いまやEXCELで誰でも簡単にできるようになった「最小二乗法」に続いていくプロセスが話的に面白いかなと思ったのが理由です。
よく知っているはずの「平均」**を、再度一緒に考え直してみましょう。
(記号にびっくりされてしまう方に)
ここで、この記事を読むのに必要な記号の意味を書いておきたいと思います。
必要のない方は、ここは飛ばして読み進めて頂ければと思います。
厳めしい、いかにも難しそうな記号が並んでいるように見えますが、これらは単なる
書き方 と 計算ルール
です。
その意味するところは、皆さんがよく知っている
足し算、引き算、掛け算、割り算
です。
何も難しくはありません。
どうか記号アレルギーを起こさず、読んで頂ければと思います。
「$\sum$」は「シグマ記号」といい、「総和」を表すために用います。
$\sum_{i=1}^{n}a_i$ とあったとき、$i$は添字といい、この場合$1~n$まで変化します。
「この$i$という添字が変化する分だけ、後ろの数を足しなさい」という意味です。
なので、この場合は $a_1+a_2+a_3+\cdots+a_n$となります。
添字は$i$以外にも$j$だったり$k$だったり$h$だったりします。
意味が分かれば何でも構いません。
「$\sum$」があったら「足す」という意味です。
いくつか例を示しますので、意味を理解していただければと思います。
\begin{eqnarray}
\sum_{i=1}^{10}i&=&1+2+3+4+5+6+7+8+9+10\\
\sum_{s=1}^{5}8&=&8+8+8+8+8\\
&=&5 \times 8 \\
\sum_{j=0}^{n}j^2&=&0^2+1^2+2^2+\cdots+n^2 \\
\sum_{i=1}^{n}\sum_{j=1}^{m}a_j &=& \sum_{j=1}^{m}a_j + \sum_{j=1}^{m}a_j + \sum_{j=1}^{m}a_j + \cdots + \sum_{j=1}^{m}a_j\\
&=& n\sum_{j=1}^{m}a_j \\
&=& n(a_1+a_2+\cdots+a_m) \\
\sum_{i=0}^{n}\sum_{j=1}^{m}a_i b_j&=&a_0b_1+a_0b_2+\cdots+a_0b_m \\
&& + a_1b_1+a_1b_2+\cdots+a_1b_m\\
&& + \cdots \\
&& + \cdots \\
&& + a_nb_1+a_nb_2+\cdots+a_nb_m
\end{eqnarray}
なので、例えば3つの値の平均は
\begin{eqnarray}
\frac{1}{3}\sum_{i=1}^{3}a_i &=& \frac{1}{3}(a_1+a_2+a_3)\\
&=& \frac{a_1+a_2+a_3}{3}
\end{eqnarray}
この$3$を$n$に変えると、$n$個の場合の相加平均の式になります。
もう一つ、行列というものを使います。
行列は以下のような方法で計算を行います。
\begin{eqnarray}
\left[\begin{array}{c}
a \\ b \\ c
\end{array}\right]
+
\left[\begin{array}{c}
d \\ e \\ f
\end{array}\right]
&=&
\left[\begin{array}{c}
a+d \\ b+e \\ c+f
\end{array}\right] \\
\left[\begin{array}{cc}
a & d \\
b & e \\
c & f
\end{array}\right]
+
\left[\begin{array}{c}
g & j \\
h & k \\
i & l
\end{array}\right]
&=&
\left[\begin{array}{cc}
a+g & d+j \\
b+h & e+k \\
c+i & f+l
\end{array}\right] \\
\\
\left[\begin{array}{ccc}
a & b & c
\end{array}\right]
\left[\begin{array}{c}
d \\ e \\ f
\end{array}\right]
&=&
ad + be + cf \\
\left[\begin{array}{c}
a \\ b \\ c
\end{array}\right]
\left[\begin{array}{ccc}
d & e & f
\end{array}\right]
&=&
\left[\begin{array}{ccc}
ad & ae & af \\
bd & be & bf \\
cd & ce & cf
\end{array}\right] \\
\left[\begin{array}{cc}
a & d \\
b & e \\
c & f
\end{array}\right]
\left[\begin{array}{ccc}
g & h & i\\
j & k & l\\
\end{array}\right]
&=&
\left[\begin{array}{ccc}
ag+dj & ah+dk & ai+dl\\
bg+ej & bh+ek & bi+el\\
cg+fj & ch+fk & ci+fl
\end{array}\right]
\end{eqnarray}
掛け算の基本は 横 ⇒ 縦 です。
また、逆行列というものが出てきます。
これは「割り算」をするようなものです。
a \times \frac{1}{a} = 1
と同じように、$A$を行列として、
A A^{-1} = A^{-1}A = E
ここで$E$は単位行列と呼ばれるもので、数字の$1$に相当します。
$1$と同じなので、この単位行列$E$をある行列$A$にかけても$AE=EA=A$、$A$のままです。
これを、
\begin{eqnarray}
ab&=&c \\ \\
\left(\frac{1}{a}\right)ab &=& \left(\frac{1}{a}\right)c \\
1 \cdot b&=&\left(\frac{1}{a}\right)c \\
∴ b &=& \frac{c}{a}
\end{eqnarray}
と同じように、
\begin{eqnarray}
AB&=&C \\ \\
A^{-1}AB&=&A^{-1}C \\
EB &=& A^{-1}C \\
∴ B &=& A^{-1}C
\end{eqnarray}
のように使います。
もう一度繰り返しますが、これらはただの書き方でありルールです。
意味するところは四則演算であり何も難しいことはありません。
内容もさして難解ではありませんので、アレルギーを起こさずゆっくり読み解いて頂ければと思います。
では、本編へもどりましょう。
相加平均
平均といってもいろいろな平均があります。
相加平均、相乗平均、調和平均、加重平均。
一般化平均なんてものもあります。
その中で、今回は 「相加平均」 のお話です。
以下「平均=相加平均」としている箇所が多々ありますが、細かいところはお気になさらず平にご容赦ください。
〇平均の平均=平均?
平均の平均って平均でしょうか?
何を言っているかですが、
ある数値列Aがありこの数値列Aを任意に部分数値列の直和に分割した時、この部分数値列毎に相加平均をとると相加平均の数値列Bができる。
この数値列Bの相加平均は、元の数値列Aの相加平均と一致するか?
余計"?"になったかもしれませんが、こういうことです。
例えば、今ここにこのような数値があったとします。
{9, 3, 7, 8, 4, 4, 4, 9, 2, 8}
これを任意のグループに分けます。今回は3つにしてみます。
{9, 7, 4}, {8, 4}, {3, 4, 9, 2, 8}
グループ毎に平均を計算します
{6.6666}, {6}, {5.2}
この3つの平均値のさらに平均値を計算します。
{5.9555}
こんな値になりました。
さて、この数値5.9555が最初の{9, 3, 7, 8, 4, 4, 4, 9, 2, 8}の平均値と一致するのか?というのが聞いていることです。
確かめてみましょう。計算すると、
{5.8}
こんな値になりました。当然、
5.9555 ≠ 5.8
ですので、質問への答えは
平均の平均 ≠ 平均 (平均の平均は平均ではない)
です。
なんでこんな事を? と思われるかもしれません。
ですが実はこれ、しばしば目にする機会があります。
この「平均の平均」を「全体の平均値だ」として用いているケースです。
そのままこの「平均の平均」を計算している場合もありますが、おそらく「平均の平均」に該当していると気づいていないだろうケースもあります。
各グループの平均値を用いてグラフに予測線を描く
がそれに該当します。
分かってあえて使っているならいいのですが、そうでない場合は大きな判断ミスを招くこともあります。
このような計算方法を用いる場合には皆さん十分にご注意いただければと思います。
ではなぜ 「各グループの平均値を用いてグラフに予測線を描く」が「平均の平均」を計算することになるのか。
それをこれから「平均の意味」を考える事で理解していくことにしましょう。
〇相加平均値と各値との差の合計を計算してみる
平均の意味を理解する為に、平均と各値との差をとって合計してみます。
「平均って大体真ん中のことでしょ?」という認識の方が多いかと思いますので、それをより数学的にはっきりさせるために行います。
真ん中であるなら、真ん中からのプラス方向とマイナス方向にはほとんど同じだけ値があるはず。
ということは、全部足したらゼロ?
確かめるために、とりあえずやってみましょう。
ここから文字と数式を使っていきます。
まず、数字が3つある場合を考えてみます。
$a_1$, $a_2$, $a_3$
これの相加平均は
$b=\frac{a_1+a_2+a_3}{3}$
これを各値から引いたものを
$c_1=a_1-b$
$c_2=a_2-b$
$c_2=a_2-b$
として、
$c_1+c_2+c_3$
を計算しましょう。
\begin{eqnarray}
c_1+c_2+c_3 &=& (a_1-b)+(a_2-b)+(a_3-b)\\
&=& a_1+a_2+a_3-3b\\
&=& a_1+a_2+a_3-3\left(\frac{a_1+a_2+a_3}{3}\right)\\
&=& a_1+a_2+a_3-a_1-a_2-a_3\\
&=& 0
\end{eqnarray}
答えは0になりました。
数字が3つでなく$n$個あった場合はどうでしょうか?
相加平均は
b=\frac{1}{n}\sum_{i=1}^{n}a_i
なので、
\begin{eqnarray}
\sum_{i=1}^{n}(a_i-b)&=&\sum_{i=1}^{n}\left(a_i-\frac{1}{n}\sum_{j=1}^{n}a_j\right)\\
&=& \sum_{i=1}^{n}a_i-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}a_j\\
&=& \sum_{i=1}^{n}a_i-\frac{1}{n} \cdot n \sum_{j=1}^{n}a_j\\
&=& \sum_{i=1}^{n}a_i-\sum_{j=1}^{n}a_j\\
&=& 0
\end{eqnarray}
$n$個の場合もこのように0になります。
どんな数字が何個あっても、各値と相加平均値との差を全部合計したら0になるということが分かりました。
〇各値との差の合計が0になるような値は?
今度は逆を考えてみます。
各値との差の合計が0になるような値はどんな値でしょうか?
再び数字が3つの場合で考えてみましょう。
$a_1$, $a_2$, $a_3$
があって、
$c_1=a_1-b$
$c_2=a_2-b$
$c_3=a_3-b$
とします。そして、
$c_1+c_2+c_3=0$
であるとき、この $b$ がどんな値なのかを知りたいわけです。
さっき相加平均がこの $b$ を満たすことは分かりました。ほかにもあるのでしょうか?
求めてみます。
\begin{eqnarray}
c_1+c_2+c_3&=&0\\
(a_1-b)+(a_2-b)+(a_3-b)&=&0\\
a_1+a_2+a_3-3b&=&0\\
\\
3b&=&a_1+a_2+a_3\\
\\
∴ b&=&\frac{a_1+a_2+a_3}{3}
\end{eqnarray}
相加平均になりました。一般の場合も計算すると、
\begin{eqnarray}
\sum_{i=1}^{n}(a_i-b)&=&0\\
\sum_{i=1}^{n}a_i-\sum_{i=1}^{n}b&=&0\\
\sum_{i=1}^{n}a_i-nb&=&0\\
nb&=&\sum_{i=1}^{n}a_i\\
\\
∴ b&=&\frac{1}{n}\sum_{i=1}^{n}a_i
\end{eqnarray}
こちらも同じく相加平均になりました。
以上の結果より、
相加平均以外の数値で各値との差の合計が0になる数値はない
ことがわかりました。
言い直せば、
各値との差の合計が0になるような数値は相加平均値である
相加平均値は各値との差の合計が0になる
b=\frac{1}{n}\sum_{i=1}^{n}a_i \ \Leftrightarrow \ \exists b \left(\sum_{i=1}^{n}(a_i-b)=0 \right)
これがまさしく相加平均の意味と言えます。
平均を拡張する
〇データの平均に対して線を引く?
データ収集をしていて、こんなデータが得られた時の事を考えましょう。
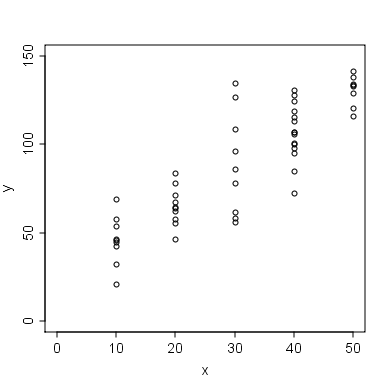
各 $x$の値に対し、$y$の値がいくつか観測されているデータです。
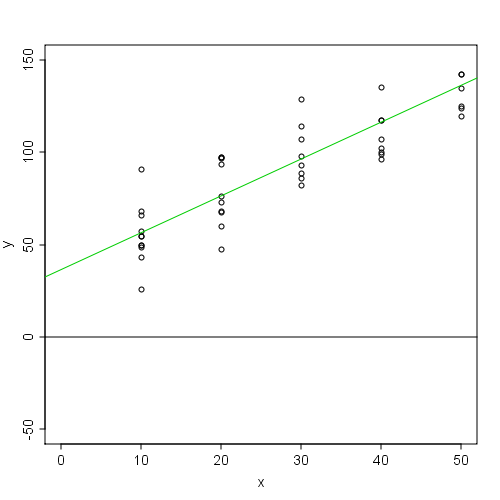
こういうデータがあったときに時々見かけるのが(上でもお話しした)各 $x$の値毎に平均値を出して、それに最小二乗法を適用して直線を引いた分析結果です。
つまりこんな感じ。
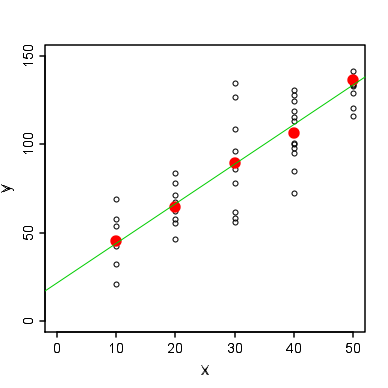
赤点が各平均です。
この赤点に対して最小二乗法で直線をプロットしています。
はてさて、この手法は正しいんでしょうか?
〇平均の意味から解釈を拡大
上では各$x$毎に平均を出して、その平均値に対して「それっぽい直線」を引きました。
では私たちがこの「それっぽい直線」を引くとき、この直線に期待していることは何でしょうか?
そもそも、私たちはなんの為に一体どんな線を引きたいんでしょうか?
私たちが平均値を求めるときは、その数値たちを代表するひとつの値を知りたい場合でしょう。
ではなぜ平均値を代表値にするかというと、「だいたい真ん中くらいの値だから」「数値たちの集団としての位置が分かるから」というのが理由かと思います。
(実際相加平均値は「真ん中」ではなく「重心」になります。なので、「数値たちの集団としての位置」を重心の位置とみなすのはそれなりに理に適っています)
同じように、こういうデータに対して直線を引きたいときは、この数値たちを代表する一本の線を引きたいというのが理由ではないかと思います。
つまり、
平均値を知れば、その値たちの大体の位置(大きさ)が把握できる
と同じように
その直線を知れば、そのデータ達の大体の傾向が把握できる
理由はこんなイメージではないでしょうか?
これは平均値のアナロジーです。
各$x$毎の平均に対して直線を引こうと思い当たるのもまっとうに思えます。
各$x$毎の代表値に対して線を引くので、その各$x$毎の代表の代表はみんなの代表であろう、ということですね。
(なんかだか政治みたいですね)
ですが、残念ながらこの方法には数学的根拠がありません。
そこで、平均値のアナロジーを使って「根拠のある」その直線を求めてみたいと思います。
再度ここで相加平均の意味を思い出してみましょう。
「各値との差の合計が0になるような数値は相加平均値である」
「相加平均値は各値との差の合計が0になる」
でした。
この意味をそのままに、相加平均を「値」から「直線」へ拡張してみましょう。
すなわち、直線からの各値の差の合計が0になる直線です。
〇平均から平均の意味を持つ関数へ
平均の意味を持つ「直線」を導こうと上で話ましたが、何も「直線」に限定する理由は実はありません。
「直線」も含む**「関数$f(x)$」**としても差し支えないのです。
直線も$f(x)=a_1+a_2x$という関数ですから。
ここではこの「関数$f(x)$」を、
- 既知の関数の線形結合で表される関数
とします。つまり、
f(x)=\sum_{k=1}^{l}a_k g_k(x)
です。この$g_k(x)$に既知の関数が入ります。$a_k$は係数です。$l$は足し合わせている関数の個数です。
$l=2$、$g_1(x)=x^0=1$、$g_2(x)=x^1=x$とすれば、
\begin{eqnarray}
f(x)&=&\sum_{k=1}^{2}a_k g_k(x)\\
&=&a_1\cdot x^0+a_2\cdot x^1\\
&=&a_1+a_2x
\end{eqnarray}
となり、直線の式になります。
つまり直線に限定せずともこの$f(x)$を求めればちゃんと直線の場合も求まるということ。
よって、この既知の関数の線形結合で表される関数$f(x)$を求めましょう。
直線からの各値の差の合計が0になる直線 改め $f(x)$からの各値の差の合計が0になる関数$f(x)$
を求めます。
この$f(x)$が相加平均を拡張した関数、いわば相加平均値ならぬ相加平均関数となってくれるはずです。
相加平均値を導き出した時の出発点は
$c_1=a_1-b$
$c_2=a_2-b$
$c_3=a_3-b$
と
$c_1+c_2+c_3=0$
でした。
この$b$を求めたい関数$f(x)$に置き換えます。
さらに今回はいろいろな$x$に対して複数の$y$がありますので、添字も二つ使います。
少し例を書くと、
- $x_1$の時のデータ$y_{11}$, $y_{12}$, $y_{13}$, $\cdots$, $y_{1j}$, $\cdots$
- $x_2$の時のデータ$y_{21}$, $y_{22}$, $y_{23}$, $\cdots$, $y_{2j}$, $\cdots$
- $x_i$の時のデータ$y_{i1}$, $y_{i2}$, $y_{i3}$, $\cdots$, $y_{ij}$, $\cdots$
という具合です。
前回の各数値$a$は今回の場合$y$に該当しますので、上の式を書き換えると
$c_{11}=y_{11}-f(x_1)$
$c_{12}=y_{12}-f(x_1)$
$\vdots$
$c_{21}=y_{21}-f(x_2)$
$c_{22}=y_{22}-f(x_2)$
$\vdots$
$c_{ij}=y_{ij}-f(x_i)$
$\vdots$
となり、これらの合計が
$c_{11}+c_{12}+\cdots+c_{ij}+\cdots=0$
というわけです。
これらをまとめて書けば
\begin{eqnarray}
\sum_{i=1}^{n}\sum_{j=1}^{m_i}c_{ij}
&=&
\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-f(x_i)\right) \\
&=&
0
\end{eqnarray}
ここで$n$は$x$の個数、$m_i$は各$x_i$でのデータ$y$の個数になります。
よって、全データ数($y$の個数)は
m_1+m_2+\cdots+m_n=\sum_{i=1}^{n}m_i
です。
(ここで平均の平均を求めた時の部分平均の話を思い出された方はスルドイ)
また、以降この全データ数($y$の個数)を添え字なしの$m$で表します。
\begin{eqnarray}
m
&=& \sum_{i=1}^{n}m_i \\
&=&m_1+m_2+\cdots+m_n
\end{eqnarray}
〇「相加平均関数」の導出
上の式を出発点に$f(x)$を求めていきます。
$f(x)$は既知の関数$g_k(x)$の線形結合 $f(x)=\sum_{k=1}^{l}a_k g_k(x)$ で表されるとしましたから、$g_k(x)$自体は既に分かっています(というより、決める)。
直線の例では$g_1(x)=1$、$g_2(x)=x$という具合でした。
なので今わかっていないのは、この$g_k(x)$たちにかかる係数$a_k$たちです。
この係数$a_k$たちが全部わかれば、$f(x)$が求まった、ということになります。
ではさっそく$a_k$たちを求めに行きましょう。
\begin{eqnarray}
\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-f(x)\right)=0\\
\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-\sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)=0\\
\sum_{i=1}^{n}\left(\sum_{j=1}^{m_i}y_{ij}-m_i \sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)=0\\
\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}-\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)=0\\
∴ \sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}
\end{eqnarray}
ここまで式変形したところで困ってしまいました。
求めたい係数=未定定数が $l$個あるのに式が1つしかありません。
このままでは係数$a_k$たちが求まらないことになります。
ここで出発点に立ち戻ってみます。
今の目的は「各値との差の合計が0になる関数$f(x)$」を求めることです。
最終的にこれを満たせればいい。
そこで、この式から$l$個の式を作り出してしまいましょう。
どうやって作るか?
$l$個の式を作りたいのだから$l$個あるものを使います。
今「$l$個ある既知の使えるもの」といえば$g_k(x)$たちです。
この$1~l$ まである、各$g_k(x_i)$を上式の両辺の各項に掛けたものを用意しましょう。
右辺と左辺で項の数は一緒ですし、対応する$x$の値も順番は同一です。
等号は成り立つようにこれから$a_k$を求めるのでいまは問題になりません。
この方法の正当性は後で「差の合計が0」になるかどうかを確かめることではっきりさせましょう。
こうすると、めでたく$l$個の独立した式が出来上がります。
\begin{eqnarray}
\left\{
\begin{array}{c}
\sum_{i=1}^{n} m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)g_1(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}g_1(x_i)\\
\sum_{i=1}^{n} m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)g_2(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}g_2(x_i)\\
\vdots\\
\sum_{i=1}^{n} m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)g_l(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}g_l(x_i)
\end{array}
\right.
\end{eqnarray}
(なお、ここで両辺に掛ける$g_k(x)$たちは一次独立であるとします。このあたり詳しく知りたい方は線形代数の専門書をご参照ください。)
どの式も形は同じなので以下の式で代表することにします。
\begin{eqnarray}
\sum_{i=1}^{n}m_i \sum_{k=1}^{l}a_{k}g_{k}(x_i)g_h(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}g_h(x_i) (1 \leq h \leq l, \ h \in \mathbb{N}) \tag{☆}
\end{eqnarray}
先ほどの式は一つの式、こちらは$l$個の式です。$h$について和がとられていないことに注意してください。
これを行列表記にしてやります。
\begin{eqnarray}
{\scriptstyle
\sum_{i=1}^{n}
\left(\left[
\begin{array}{cccc}
m_i g_1(x_i)g_h(x_i) & m_i g_2(x_i)g_h(x_i) & \cdots & m_i g_l(x_i)g_h(x_i)
\end{array}\right]
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right]\right)
}
=
{\scriptstyle
\sum_{i=1}^{n}
\left(\left[
\begin{array}{cccc}
g_h(x_i) & g_h(x_i) & \cdots & g_h(x_i)
\end{array}
\right]\left[
\begin{array}{c}
y_{i1}\\ y_{i2}\\ \vdots \\ y_{im_i}
\end{array}
\right]\right)\\
}
\\
{\scriptstyle
\sum_{i=1}^{n}
\left(\left[
\begin{array}{cccc}
g_h(x_i) & g_h(x_i) & \cdots & g_h(x_i)
\end{array}
\right]\left[
\begin{array}{cccc}
g_1(x_i) & g_2(x_i) & \cdots&g_l(x_i)\\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i)
\end{array}
\right]\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots\\ a_l
\end{array}
\right]\right)
}
=
{\scriptstyle
\sum_{i=1}^{n}\left(\left[\begin{array}{cccc}g_h(x_i)&g_h(x_i)&\cdots&g_h(x_i)\end{array}\right]\left[\begin{array}{c}y_{i1}\\y_{i2}\\\vdots\\y_{im_i}\end{array}\right]\right)\\
}
\\
{\scriptstyle
\left[
\begin{array}{cccccccccc}
g_h(x_1) & \cdots & g_h(x_1) & g_h(x_2) & \cdots & g_h(x_2) & \cdots \cdots & g_h(x_n) & \cdots & g_h(x_n)
\end{array}
\right]
\left[
\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \vdots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}
\right]
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots\\ a_l
\end{array}
\right]\\
}
\\ =
{\scriptstyle
\left[
\begin{array}{cccccccccc}
g_h(x_1) & \cdots & g_h(x_1) & g_h(x_2) & \cdots & g_h(x_2) & \cdots \cdots & g_h(x_n) & \cdots & g_h(x_n)
\end{array}
\right]
\left[
\begin{array}{c}
y_{11}\\ \vdots\\ y_{1m_1}\\ y_{21}\\ \vdots\\ y_{2m_2}\\ \vdots\\ y_{n1}\\ \vdots\\ y_{nm_n}
\end{array}
\right]
}
\end{eqnarray}
これは$h$で代表して表記した式だったので、$l$個の式をすべてまとめ表記しなおしてやれば、
\begin{eqnarray}
\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}\right]
\left[\begin{array}{c}
a_1\\ a_2\\ \vdots\\ a_l
\end{array}\right]\\
=\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{c}
y_{11}\\ \vdots\\ y_{1m_1}\\ y_{21}\\ \vdots\\ y_{2m_2}\\ \vdots\\ y_{n1}\\ \vdots\\ y_{nm_n}
\end{array}\right]
\end{eqnarray}
左辺最初の二つの行列は計算すると$l \times l$の正方行列になりますので、これが正則行列であるとすれば逆行列が存在して、
\begin{eqnarray}
&&
{\scriptstyle
\left[\begin{array}{c}
a_1\\ a_2\\ \vdots\\ a_l
\end{array}\right]
=}\hspace{5em}\\
&&
{\scriptstyle
\left[
\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}\right]
\right]^{-1}
\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{c}
y_{11}\\ \vdots\\ y_{1m_1}\\ y_{21}\\ \vdots\\ y_{2m_2}\\ \vdots\\ y_{n1}\\ \vdots\\ y_{nm_n}
\end{array}\right]
}
\end{eqnarray}
これを計算すれば係数$a_k$が全部求まるので、見事、$f(x)$が求まりました!
〇確かめる
いま求めた係数$a_k$たちを持つ関数$f(x)$が本当に**「拡張された平均」**の要件を満たしているか確かめましょう。
そのためには
- $f(x)$からの各値の差の合計が0
を確かめればよいのでした。
これは以下を計算してみれば確かめられます。
I=\sum_{i=1}^{n}\sum_{j=1}^{m_i}(y_{ij}-f(x_i))
この$I$が0であれば成功です。
先ほど導出の途中で「ひとつの式を$l$個に増やす」ということもしてますので、これの正当性も確かめることになります。
まず、先ほどと同じ式展開をします。
\begin{eqnarray}
I&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-f(x)\right)\\
&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-\sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)\\
&=&\sum_{i=1}^{n}\left(\sum_{j=1}^{m_i}y_{ij}-m_i \sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)\\
&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}-\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)\\
\end{eqnarray}
ここで、
\begin{eqnarray}
\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}=
\left[\begin{array}{ccccc}
1 & 1 & \cdots & 1
\end{array} \right]
\left[\begin{array}{c}
y_{11} \\ y_{12} \\ \vdots \\ y_{1m_1} \\ y_{21} \\ \vdots \\ y_{2m_2} \\ y_{31} \\ \vdots \\ \vdots \\ y_{nm_n}
\end{array}\right]
\end{eqnarray}
なので、
\begin{eqnarray}
\boldsymbol{e}=\left[\begin{array}{c} 1\\ 1\\ \vdots\\ 1 \end{array}\right],\hspace{2em}
\boldsymbol{y}=\left[\begin{array}{c}
y_{11} \\ y_{12} \\ \vdots \\ y_{1m_1} \\ y_{21} \\ \vdots \\ y_{2m_2} \\ y_{31} \\ \vdots \\ \vdots \\ y_{nm_n}
\end{array}\right]
\end{eqnarray}
と置くと、
\begin{eqnarray}
\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}=\boldsymbol{e}^{t} \boldsymbol{y}
\end{eqnarray}
また、
\begin{eqnarray}
\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)
&=&
\sum_{i=1}^{n}
\left(\left[
\begin{array}{cccc}
m_i g_1(x_i) & m_i g_2(x_i) & \cdots & m_i g_l(x_i)
\end{array}\right]
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right]\right) \\
&=&
\sum_{i=1}^{n}
\left(
\left[
\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left[
\begin{array}{cccc}
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i) \\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i) \\
\vdots & \vdots & \ddots & \vdots \\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i)
\end{array}\right]
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right]
\right) \\
&=&
\left[
\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left(
\sum_{i=1}^{n}
\left[\begin{array}{cccc}
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i) \\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i) \\
\vdots & \vdots & \ddots & \vdots \\
g_1(x_i) & g_2(x_i) & \cdots & g_l(x_i)
\end{array}\right]
\right)
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right] \\
&=&
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left(
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left[
\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \vdots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}
\right]
\right)
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right] \\
&=&
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left[
\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \vdots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}
\right]
\left[
\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}
\right]
\end{eqnarray}
ここでまた
\begin{eqnarray}
G =\left[
\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \vdots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}
\right]
,\hspace{2em}
\boldsymbol{a}=\left[\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}\right]
\end{eqnarray}
と置くと、
\begin{eqnarray}
\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)=\boldsymbol{e}^{t} G \boldsymbol{a}
\end{eqnarray}
これより、
\begin{eqnarray}
I&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}(y_{ij}-f(x_i)) \\
&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}-\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i) \\
&=&\boldsymbol{e}^{t}\boldsymbol{y}-\boldsymbol{e}^{t} G \boldsymbol{a} \\
&=&\boldsymbol{e}^{t}(\boldsymbol{y}- G \boldsymbol{a})
\end{eqnarray}
と表されます。
さて、係数$a_k$たちを求めた式を思い出し、ここで置き換えた記号を使うと
\begin{eqnarray}
\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}\right]
\left[\begin{array}{c}
a_1\\ a_2\\ \vdots\\ a_l
\end{array}\right]\\
=\left[\begin{array}{cccccc}
g_1(x_1) & g_1(x_1) & \cdots & g_1(x_n) & g_1(x_n)\\
g_2(x_1) & g_2(x_1) & \cdots & g_2(x_n) & g_2(x_n)\\
\vdots & \vdots & \ddots & \vdots & \vdots\\
g_l(x_1) & g_l(x_1) & \cdots & g_l(x_n) & g_l(x_n)
\end{array}\right]
\left[\begin{array}{c}
y_{11}\\ \vdots\\ y_{1m_1}\\ y_{21}\\ \vdots\\ y_{2m_2}\\ \vdots\\ y_{n1}\\ \vdots\\ y_{nm_n}
\end{array}\right]
\end{eqnarray}
は
\begin{eqnarray}
G^{t} G \boldsymbol{a}= G^{t}\boldsymbol{y}
\end{eqnarray}
と表されます。
さらに変形すると、
\begin{eqnarray}
G^{t}(\boldsymbol{y} - G \boldsymbol{a})=O
\end{eqnarray}
さて、
\begin{eqnarray}
I&=&\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a})
\end{eqnarray}
において、係数の$\boldsymbol{a}$は上式で導出した$\boldsymbol{a}$、$\boldsymbol{y}$と$G$は予め与えられたものであるので同じものです。
これらを用いると、
\begin{eqnarray}
I&=&\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a})=O
\end{eqnarray}
が(条件付きですが)言えるので、めでたく0になり求めた係数$a_k$たちを持つ関数$f(x)$が本当に 「拡張された平均」 の要件を満たしていることが分かります。
最後の大事なところをすっ飛ばしましたが、この説明はそこそこややこしいので割愛させてください。
(この割愛した説明は末尾の「おまけ」に記載してあります。)
代わりに、直線の場合においてちゃんと0になって成立することを確かめてみます。
直線の場合$f(x)$は
\begin{eqnarray}
f(x)=a_1+a_2x
\end{eqnarray}
ですので、
\begin{eqnarray}
G=
\left[\begin{array}{cc}
1 & x_1 \\
1 & x_1 \\
\vdots & \vdots \\
1 & x_2 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_{n} \\
1 & x_{n}
\end{array} \right]
=
\left[\begin{array}{cc}
1 & x_1 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_{m}
\end{array} \right]
, \hspace{2em}
G^{t}=
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1 \\
x_1 & x_2 & \cdots & x_{m}\\
\end{array} \right]
\end{eqnarray}
です。添字が$1,2,\cdots,n$から$m$に変わっているのは、並んでいる順に番号を新に付け替えたと理解してください。
すると、
\begin{eqnarray}
G^{t}G=
\left[\begin{array}{cc}
m & \sum_{i=1}^{m}x_i \\
\sum_{i=1}^{m}x_i & \sum_{i=1}^{m}x_i^{2} \\
\end{array} \right]
, \hspace{2em}
(G^{t}G)^{-1}=
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{cc}
\sum_{i=1}^{m}x_i^{2} & -\sum_{i=1}^{m}x_i \\
-\sum_{i=1}^{m}x_i & m\\
\end{array} \right]
\end{eqnarray}
ここから$\boldsymbol{a}$を求めると、
\begin{eqnarray}
\boldsymbol{a}&=&(G^{t}G)^{-1}G^{t}\boldsymbol{y} \\
&=&
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{cc}
\sum_{i=1}^{m}x_i^{2} & -\sum_{i=1}^{m}x_i \\
-\sum_{i=1}^{m}x_i & m\\
\end{array} \right]
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1 \\
x_1 & x_2 & \cdots & x_{m}\\
\end{array} \right]
\left[\begin{array}{c}
y_{1} \\ y_{2} \\ \vdots \\ y_{m}
\end{array}\right] \\
&=&
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{c}
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i \\
m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i
\end{array}\right]
\end{eqnarray}
ここから先に$G\boldsymbol{a}$を求めておくと、
\begin{eqnarray}
G\boldsymbol{a}
&=&
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{cc}
1 & x_1 \\
1 & x_2 \\
\vdots & \vdots \\
1 & x_{m}
\end{array} \right]
\left[\begin{array}{c}
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i \\
m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i
\end{array}\right] \\
&=&
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{c}
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_1(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_2(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\vdots \\
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_{m}(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\end{array}\right]
\end{eqnarray}
これを$I$に代入するのですが、計算しやすいようにいったん展開して代入します。
\begin{eqnarray}
I
&=&\boldsymbol{e}^{t}(\boldsymbol{y}- G \boldsymbol{a}) \\
&=&\boldsymbol{e}^{t}\boldsymbol{y}-\boldsymbol{e}^{t} G \boldsymbol{a} \\
&=&
{\scriptstyle
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left[\begin{array}{c}
y_{1} \\ y_{2} \\ \vdots \\ y_{m}
\end{array}\right]
-
}
\\
&&
{\scriptstyle
\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left[\begin{array}{cccc}
1 & 1 & \cdots & 1
\end{array}\right]
\left[\begin{array}{c}
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_1(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_2(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\vdots \\
\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_i y_i + x_{m}(m\sum_{i=1}^{m}x_i y_i - \sum_{i=1}^{m}x_i \sum_{i=1}^{m}y_i)\\
\end{array}\right]
}
\\
&=&
\sum_{i=1}^{m}y_i - \\
&&\frac{1}{m\sum_{i=1}^{m}x_i^{2} - (\sum_{i=1}^{m}x_i)^{2}}
\left\{
m\sum_{i=1}^{m}x_i^{2} \sum_{i=1}^{m}y_i - m\sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_iy_i + m\sum_{i=1}^{m}x_i \sum_{i=1}^{m}x_iy_i - (\sum_{i=1}^{m}x_i)^{2} \sum_{i=1}^{m}y_i
\right\} \\
&=&
\sum_{i=1}^{m}y_i - \sum_{i=1}^{m}y_i \\
&=& 0
\end{eqnarray}
よって $I=0$。
めでたく求めた係数$a_1、a_2$をもつ直線$f(x)=a_1+a_2x$が 「拡張された平均」 の要件を満たしていることが分かりました。
最小二乗法とその意味
〇拡張された平均と最小二乗法
先ほど導出した拡張された平均の関数を決める係数$\boldsymbol{a}$を求める式、
\begin{eqnarray}
G^{t}G\boldsymbol{a} = G^{t}\boldsymbol{y}
\end{eqnarray}
は、実は最小二乗法の係数を求める式と同一です。
最小二乗法では二乗誤差を最小にするため、二乗誤差の総和を偏微分して0と置きます。
二乗誤差の総和は
\begin{eqnarray}
J=\sum_{i=1}^{n}(f(x_i)-y_i)^{2}
\end{eqnarray}
です。先ほどとは二乗しているかどうかが違います。
$y$と$f(x)$の順序が違うのは特に問題ありません。
これを各$a_k$で偏微分して0と置いた
\begin{eqnarray}
\frac{\partial J}{\partial a_k}
&=&
\frac{\partial}{\partial a_k}\left\{\sum_{i=1}^{n}(f(x_i)-y_i)^2\right\} \\
&=&
\frac{\partial}{\partial a_k}\left\{\sum_{i=1}^{n}\left(\sum_{j=1}^{m}a_jg_j(x_i)-y_i\right)^2\right\} \\
&=&
2\sum_{i=1}^{n}\left(\sum_{j=1}^{m}a_jg_j(x_i)-y_i\right)\frac{\partial}{\partial a_k}\left(\sum_{j=1}^{m}a_jg_j(x_i)-y_i\right) \\
&=&
2\sum_{i=1}^{n}\left(\sum_{j=1}^{m}a_jg_j(x_i)-y_i\right)g_k(x_i) \\
&=&
2\sum_{i=1}^{n}\sum_{j=1}^{m}a_jg_j(x_i)g_k(x_i)-2\sum_{i=1}^{n}y_ig_k(x_i) \\
&=&
0 \\
\\
∴ &&\sum_{i=1}^{n}\sum_{j=1}^{m}a_jg_j(x_i)g_k(x_i)=\sum_{i=1}^{n}y_ig_k(x_i)
\end{eqnarray}
これらの連立方程式を解いて係数$a_k$たちを求めます。
この式は(☆)と同じ式です。
(☆)式は$m_i$が入っているため見た目若干違うように見えますが、添字の番号を振りなおせばまったく同一になります。
行列表記にしてやればどちらも
\begin{eqnarray}
G^{t}G\boldsymbol{a} = G^{t}\boldsymbol{y}
\end{eqnarray}
となりおんなじです。
これを改めていえば、
「拡張された平均の関数を求めた」→「最小二乗法になった」
ということ。
つまり、
最小二乗法を適用する = 拡張された平均を求める
と言えるわけです。
これで冒頭あたりにお話ししたことがお分かり頂けるかと思います。
各$x$毎にとった平均値に対して最小二乗法を適用することは、平均の平均を計算していることと同じ
なのです。
平均の平均 ≠ 平均ですから、各平均値に対して最小二乗法を適用する手法は正しいとは言い難いと結論できるかと思います。
各$x$毎の代表の代表はみんなの代表ではない
ということです。
(なんだかアメリカの大統領選挙で騒がれている事を思い出させますね。タイムリー)
平均値に対して最小二乗法を適用する方法は、理由がない限り避けることをお勧めいたします。
〇拡張された平均=最小二乗法のイメージ
これまでの話を図的に見てみることにします。
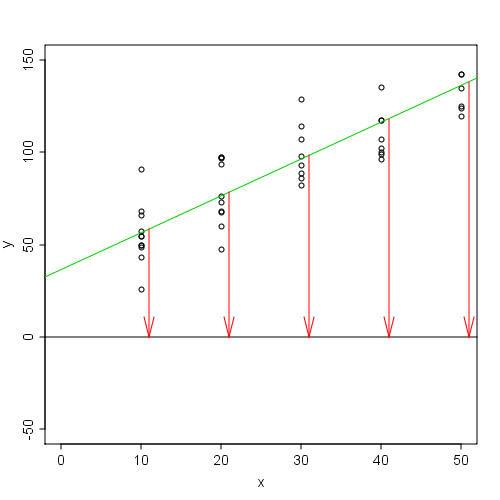
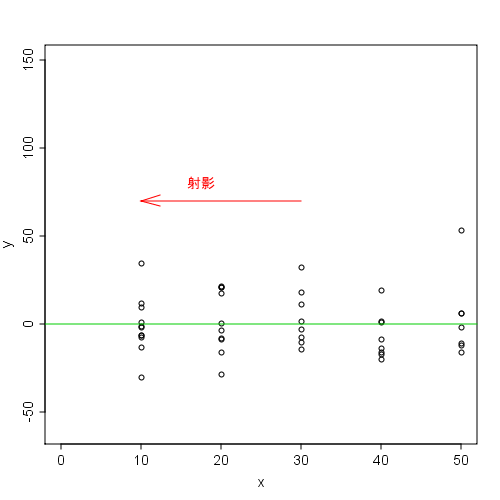
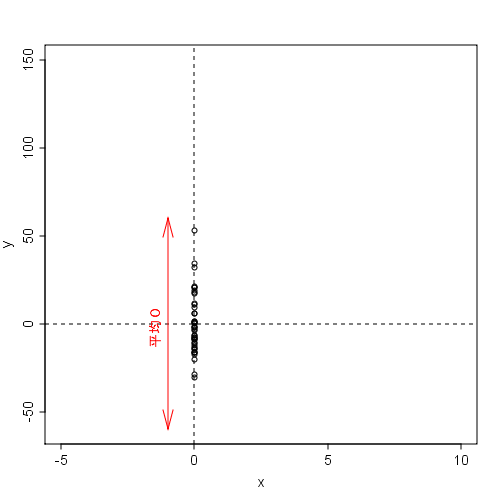
- 散布図に最小二乗法で線を引き
- その線をx軸と見立てる(回転させずにそのまま下にずらす)【(値 - 平均) を行っている】
- データ全部をy軸に射影すると
- その平均が0になる。【(値 - 平均) を全部足したら0】
これまでの話はイメージ的にこれを逆に辿ったわけでして、結果は最小二乗法で求まる線が出てきましたよ、ということです。
なので、最小二乗法が平均を拡張したものだ、というイメージも頷いていただけるかと思います。
終わりに
最小二乗法は拡張された相加平均を求める方法
これがなんとなくご納得いただけたらこの記事は成功です。
相加平均に関する理解、深めていただけたでしょうか?
相加平均一つとっても、ちゃんと考えるとこんな風に応用や関連が見えてくるのは面白いですね。
また別の発展としては、同じ相加平均を「重心だ!」ととらえて発展させていくと主成分分析の話につながっていったりして面白いのですが、それはまた機会があれば書いてみたいと思います。
普段何気なく使っているものも、深く考察してみると思わぬ応用や発見が見つかるかもしれません。
ただ使うだけでなく、それの理論や背景、意味をちゃんと理解して使ってみると応用の幅も広がるかと思います。
皆様が見つけた新たな知見や発見も、発信してお教えいただけたらうれしく思います。
人生に卒業はない、皆で共に学び続けましょう!
Schooでは一緒に社会を変革していける仲間を募集しています。
興味がある、一緒に働きたい!などと思って頂けた方は、こちらのページをご覧いただき応募いただければ幸いです。
Wantedly -Schoo採用ページ-
ご応募お待ちしております。
おまけ
数学に抵抗がない方用に、これまでの内容をまとめておこうと思います。
上も含め、間違いなどありましたらこっそりお教えいただければ幸いです。
相加平均
相加平均は各値との差の合計が0になる値である。
b=\frac{1}{n}\sum_{i=1}^{n}a_i \ \Leftrightarrow \ \exists b \left(\sum_{i=1}^{n}(a_i-b)=0 \right)
\begin{eqnarray}
(\Rightarrow) \hspace{5em} && \\
\sum_{i=1}^{n}(a_i-b)&=&\sum_{i=1}^{n}\left(a_i-\frac{1}{n}\sum_{j=1}^{n}a_j\right)\\
&=& \sum_{i=1}^{n}a_i-\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{n}a_j\\
&=& \sum_{i=1}^{n}a_i-\frac{1}{n} \cdot n \sum_{j=1}^{n}a_j\\
&=& \sum_{i=1}^{n}a_i-\sum_{j=1}^{n}a_j\\
&=& 0
\\
(\Leftarrow) \hspace{5em} && \\
\sum_{i=1}^{n}(a_i-b)&=&0\\
\sum_{i=1}^{n}a_i-\sum_{i=1}^{n}b&=&0\\
\sum_{i=1}^{n}a_i-nb&=&0\\
nb&=&\sum_{i=1}^{n}a_i\\
\\
∴ b&=&\frac{1}{n}\sum_{i=1}^{n}a_i
\end{eqnarray}
相加平均の拡張
各値からの差の合計が0になる関数$f(x)$を求める。
〇前提
$f(x)$は既知関数の線形結合で表されるとする。
f(x)=\sum_{i=1}^{n}a_i g_i(x)
(導出)
各値との差を合計を0と置く
\begin{eqnarray}
\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-f(x)\right)=0\\
\sum_{i=1}^{n}\sum_{j=1}^{m_i}\left(y_{ij}-\sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)=0\\
\sum_{i=1}^{n}\left(\sum_{j=1}^{m_i}y_{ij}-m_i \sum_{k=1}^{l}a_{k}g_{k}(x_i)\right)=0\\
\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}-\sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)=0\\
∴ \sum_{i=1}^{n}m_i\sum_{k=1}^{l}a_{k}g_{k}(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}
\end{eqnarray}
一次独立な既知関数を各々両辺の各項に掛ける。
\begin{eqnarray}
\sum_{i=1}^{n}m_i \sum_{k=1}^{l}a_{k}g_{k}(x_i)g_h(x_i)=\sum_{i=1}^{n}\sum_{j=1}^{m_i}y_{ij}g_h(x_i) (1 \leq h \leq l, \ h \in \mathbb{N})
\end{eqnarray}
\begin{eqnarray}
G =\left[
\begin{array}{cccc}
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_1) & g_2(x_1) & \cdots & g_l(x_1)\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_2) & g_2(x_2) & \cdots & g_l(x_2)\\
\vdots & \vdots & \vdots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)\\
\vdots & \vdots & \ddots & \vdots\\
g_1(x_n) & g_2(x_n) & \cdots & g_l(x_n)
\end{array}
\right]
,\hspace{2em}
\boldsymbol{a}=\left[\begin{array}{c}
a_1\\ a_2\\ \vdots \\a_l
\end{array}\right]
,\hspace{2em}
\boldsymbol{y}=\left[\begin{array}{c}
y_{11} \\ y_{12} \\ \vdots \\ y_{1m_1} \\ y_{21} \\ \vdots \\ y_{2m_2} \\ y_{31} \\ \vdots \\ \vdots \\ y_{nm_n}
\end{array}\right]
,\hspace{2em}
\boldsymbol{e}=\left[\begin{array}{c} 1\\ 1\\ \vdots\\ 1 \end{array}\right],\hspace{2em}
\end{eqnarray}
とすれば、
\begin{eqnarray}
G^{t}G\boldsymbol{a}=G^{t}\boldsymbol{y}
\end{eqnarray}
$G^{t}G$が正則として
\begin{eqnarray}
\boldsymbol{a}=(G^{t}G)^{-1}G^{t}\boldsymbol{y}
\end{eqnarray}
(確認)
\begin{eqnarray}
I
&=&\sum_{i=1}^{n}\sum_{j=1}^{m_i}(y_{ij}-f(x_i)) \\
&=&\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a})
\end{eqnarray}
$\boldsymbol{a}$を導出した正規方程式を変形すると
\begin{eqnarray}
G^{t}(\boldsymbol{y}-G\boldsymbol{a})=O
\end{eqnarray}
$G^{t} \neq O$であるから、$(\boldsymbol{y}-G\boldsymbol{a})$は$(\boldsymbol{y}-G\boldsymbol{a})=O$もしくは零因子。
(1) $(\boldsymbol{y}-G\boldsymbol{a})=O$の場合
\begin{eqnarray}
I
&=&\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a}) \\
&=&\boldsymbol{e}^{t}O \\
&=& O
\end{eqnarray}
よって成立。
(2) $(\boldsymbol{y}-G\boldsymbol{a})$が零因子の場合
$(\boldsymbol{y}-G\boldsymbol{a})$は列ベクトルであり、$G^{t}$の零因子であるから、$G^{t}$のどの行ベクトルとも直行する。
$G^{t}$の行ベクトルは互いに一次独立であるから、これらの行ベクトルが張るベクトル空間$V$に対しての直交補空間$V^{\perp}$に対し$(\boldsymbol{y}-G\boldsymbol{a}) \in V^{\perp}$。
従って、$\boldsymbol{e} \in V$であれば$\boldsymbol{e} \perp V^{\perp}$となり$(\boldsymbol{y}-G\boldsymbol{a})$と直交、すなわち、
\begin{eqnarray}
I
&=&\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a}) \\
&=& O
\end{eqnarray}
よって成立。
一方、$\boldsymbol{e} \notin V$の場合は一般に$\boldsymbol{e}$と$(\boldsymbol{y}-G\boldsymbol{a})$の直交性は保証されない為、成立は保証されない(直交でない、すなわち成立しないことも保証されない)。
(確認終)
すなわち$\boldsymbol{e}$と$G^{t}$の行ベクトルが一次従属であることが、$\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a})=O$であることの十分条件となる。
これは$f(x)$に切片項がある場合には必ず成立することを意味する。
(切片項があれば$G$の列に$\boldsymbol{e}$が含まれる為)
なぜ必要十分にならないかといえば、一次独立な既知関数を各々両辺の各項に掛ける操作に理由がある。
これは
\begin{eqnarray}
\boldsymbol{e}^{t}(\boldsymbol{y}-G\boldsymbol{a}) = O
\end{eqnarray}
において$\boldsymbol{e}^{t}$を$G^{t}$に置き換えることを意味する。
$(\boldsymbol{y}-G\boldsymbol{a})$と$\boldsymbol{e}$は互いに互いの直交補空間に属するが、その直交補空間は一般に一意ではない。
上式の$\boldsymbol{e}^{t}$を$\boldsymbol{e}$と一次従属な行ベクトル$\{g_i\}_{i=1\dots l}$を持つ$G^{t}$に置き換える場合、
\begin{eqnarray}
G^{t}(\boldsymbol{y}-G\boldsymbol{a}) = O
\end{eqnarray}
は$\{ g_i \}_{i=1 \dots l}$の張るベクトル空間$V$に$\boldsymbol{e}$が含まれる事より$\boldsymbol{e}$と$(\boldsymbol{y}-G\boldsymbol{a})$が直交することを保証することは今見た通りである。
しかし$\{ g_i \}_{i=1 \dots l}$と$\boldsymbol{e}$が一次独立の場合は、この正規方程式は$\boldsymbol{e}$と$(\boldsymbol{y}-G\boldsymbol{a})$との間の関係を何も保証しない。
これが必要十分にならない理由である。
以上より、最小二乗法(切片項あり)は拡張された相加平均ととらえる事が可能
以上です。