これは
-
この論文を元に数式微分を支配木を使って高速にしてみました
-
かなり説明が雑なのとほぼメモのようになってしまったので, 正しく知りたい方は元論文を読んだほうがいいです
また, これもかなりインフォーマルですが数式微分から自動微分の原理(+α)を説明するスライドも作ってみたので公開します
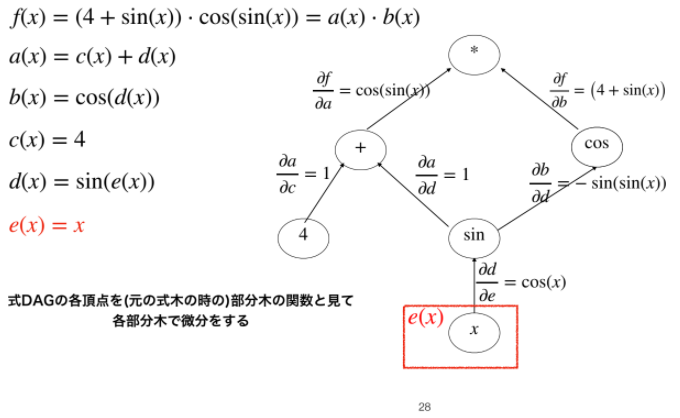
微分グラフ(Derivative graph)
冒頭にも紹介した元論文で(Derivative graph)と呼ばれているもので, 数式を表すDAGの各辺に連鎖律で必要な数式をもたせたものです.
微分の計算方法自体は自動微分と同じで, 自動微分と違うのは式そのものを辺に持っていることです.
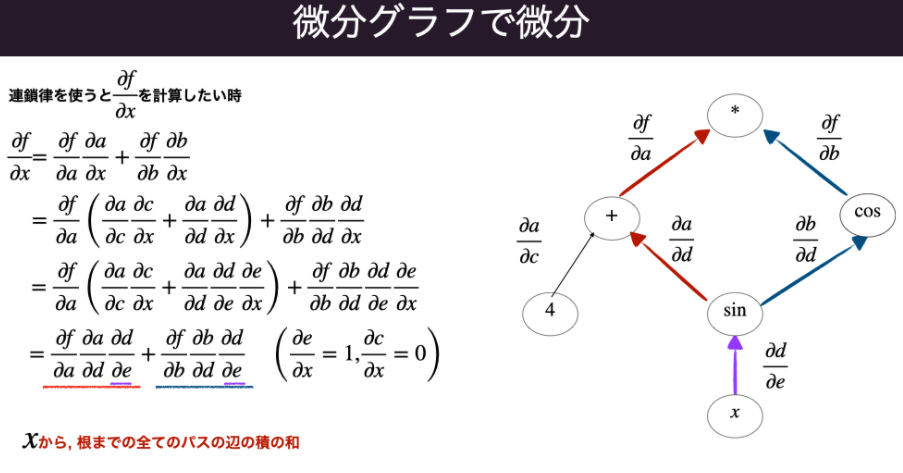
スライド引用画像の日本語が残念ですが, 変数から根のパスに現れる式全ての積を, 全てのパスについて足し合わせたものが全体の微分になります.
具体的な値で評価したいときは微分グラフの根から各変数へのパスを代入しながら計算するか(Backward), 変数から頭に向かって同様に計算すればよいです(Forward).
元の論文中では多変数多出力関数の微分をしていますが今回は1変数で出力一つの値の関数に限定して説明します.
コントロールフローグラフ(CFG)の支配関係
微分グラフは, 関数の頭(上の画像の例だと一番上の乗算ノード)をエントリーとしてコントロールフローグラフ (CFG)と見ることができます.(画像では, 辺の向きが逆ですが)
そう見た時に, 今の微分グラフの表現をコンパクトにする方法を考えます.
イメージを言うと, 上画像のように各パスを計算している時に分岐して合流している部分グラフは, 連鎖律によって展開した微分の式は因数分解できるので, 微分の意味を保ったまま微分グラフを変形させることができます.
この因数分解のできる「分岐して合流している」をCFGの支配関係を使うと定式化ができます.
支配関係の定義を見てみましょう.
CFGの支配関係の定義
CFGの2頂点$u,v$について, エントリーから$v$までの全てのパスに$u$が現れるとき, $u$が$v$をdominateすると言い, $u,, dom ,,v$と書きます. この時全ての頂点は自分自身をdominateします.
$u$から葉までの全てのパスに$v$が現れるとき, $u$が$v$をpost dominateすると言い, $u,, pdom ,,v$と書きます.
先程と同じく全ての頂点は自分自身をpost dominateします.
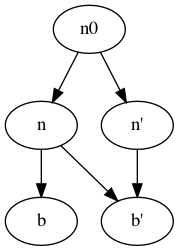
例をあげます
エントリーの$n0$は全ての点をdominateします.
$n , , dom , , b$ですが, $n , , dom , , b'$ではないです.
$b' , , pdom , , n'$ですがそれ以外の自明でない$pdom$の関係はありません.
支配関係を求めるアルゴリズム
CFGの支配関係を求めるのに最悪時計算量が$\mathcal{O}(E\log(V))$で求めるアルゴリズムが知られていますが, 漸近的計算量が$\mathcal{O}(V^2)$だけど現実のCFGのサイズでは十分高速に動作する実装が簡単なアルゴリズムがあるので, 今回はそれを使います.
微分グラフの支配木を使った簡約
支配関係を求めたあと, 微分グラフでの計算で因数分解ができる条件, つまりグラフの上だと頂点$f,b$間のグラフの一部を一つの辺に置き換えられる条件は以下のようになります.
- $f$が自分以外をdominateしていて, 出次数が2以上
- 上記の$f$に支配されていて,入次数が2以上
または
- $f$が自分以外をpost dominateしていて, 入次数が2以上
- $b$が$f$に支配されていて,出次数が2以上頂点
上記を満たす$f,b$の間の辺に対して, 必要かどうかを確認しながら辺を削除して新しい辺を追加します.
実験
$\sin(\dots(\sin(\sin(x)+\cos(x)) + \cos(\sin(x)+\cos(x))\dots) + \cos(\dots(\sin(\sin(x)+\cos(x)) + \cos(\sin(x)+\cos(x))\dots)$ のように式のグラフが鎖状になる式と
$\sin(\cos(...\sin(\cos(x)...) + \cos(\sin(...\cos(\sin(x)...)$のように
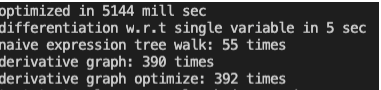
一つの円状になる式を微分して値を5秒で何回評価できるかを計測してみました.
2つの項が100回の$\cos, \sin$の繰り返しになっている式の結果
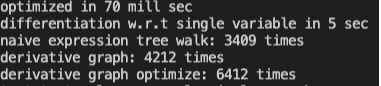
最適化にかかる時間が明らかにパスの数に依ってしまっていて実装の雑さがでています.
円の例でかろうじて最適化をしないグラフよりは速くなっているのでヨシとします.
テストコード, 内部実装ともに汚いですが コードはこちらです.
感想
大遅刻本当に申し訳ありませんでした