この記事はデータ構造とアルゴリズム Advent Calendar 2020 6日目の記事です。
はじめに
この記事では、カードゲームのソリティアと動作が似ているソートアルゴリズムPatience Sortingの紹介とその性質を利用した、最長増加列の効率的な計算方法を紹介します。
単純でありながら数列(配列)に潜む増加列、減少列の性質をうまく捉えているアルゴリズムでとても面白いアルゴリズムなので楽しんでいただけると幸いです。
ソリティアゲーム
まずネーミングの元にもなっているソリティアゲームを(大雑把に)解説します。
ソリティア(Solitaire)はカードをソートする一人用カードゲームです。
(クロンダイク(Klondike)、ペーシェンス(Patience)とも呼ばれます)
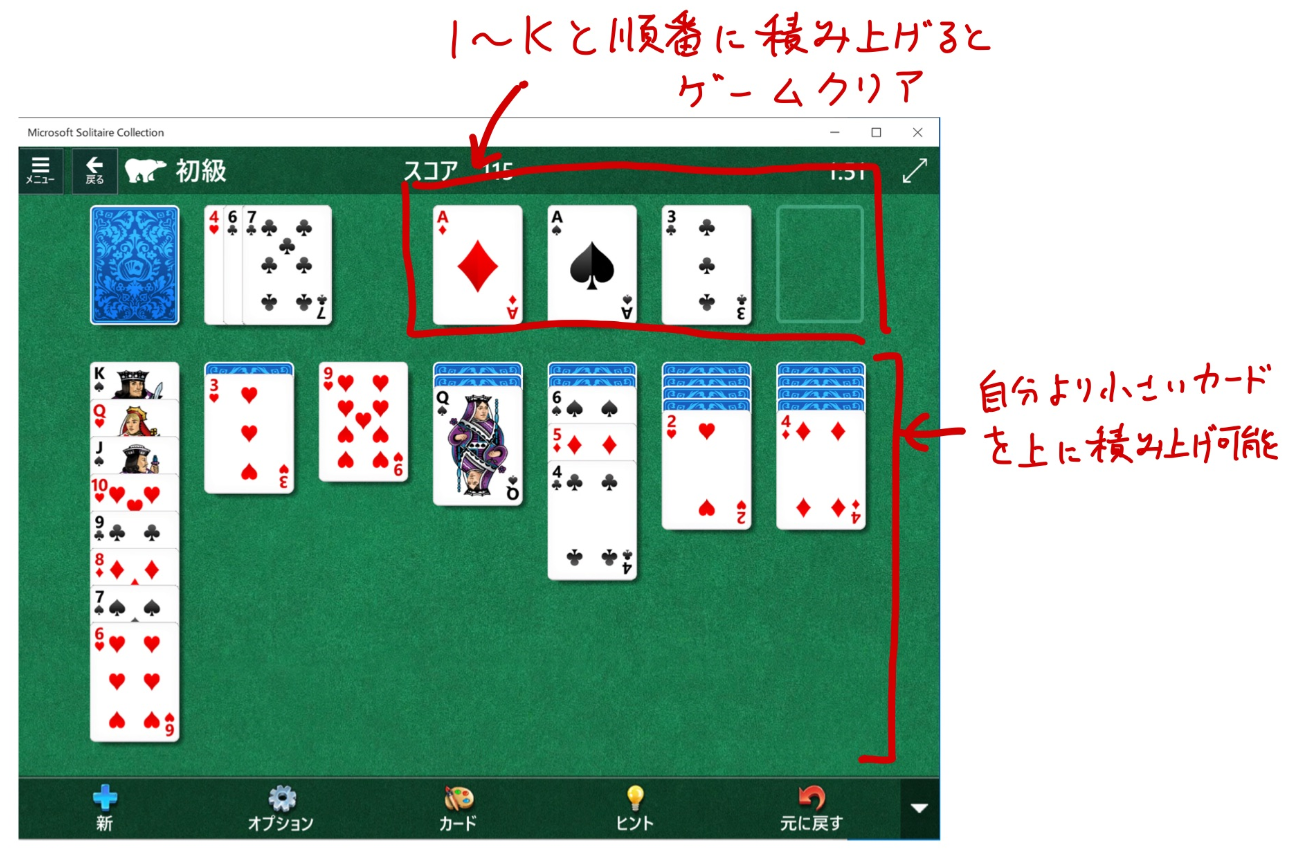
以下がソリティアのゲーム画面です。
ゲームの目的は右上上段にすべてのカードを1からKに順番に積み上げることです。
積み上げたカードをパイルと呼ぶことにします。
カードは右上上段か、下段へ移動できますが、それぞれ次の制約があります。
- 右上上段はパイルの最上段のカードより大きいカードを積み上げ可能
- 例:画像の右上上段、左から3つ目のパイルでは、♣のカードを1から3まで順番に積み上げている
- 下段はパイルの最上段のカードより小さいカードを積み上げ可能
- 例:画像の下段、一番左のパイルでは、Kから6までのカードを順番に積み上げている
このような制約から、カードの移動方法を間違えると、カードを移動できなくなったり、移動の方法がループしてしまったりとゲームクリアできなくなります。
小さいカードから大きいカードへ積み上げるパイルを増加列のパイル、逆を減少列のパイルと呼ぶことにすると、ソリティアゲームは以下のようなゲームと解釈することが出来ます。
「減少列のパイルを作成し、その情報をもとに増加列のパイルを作成する」
Patience Sortingは正に上記の戦略をとる2段階ソートアルゴリズムになっており、Step 1で配列をいくつかの減少列(逆方向ソート)に分割し、Step 2で、減少列を用いた順方向ソートを行います。
Patience Sorting
長さ$n$の配列$A$が与えられ、最小値から順番にソートした値を出力することを考えます。
簡単のため、同じ値はないものとします。
Patience Sortingの基本戦略は次のようになります。
- Step 1: $A$を左から右へ順番に読み込み、各$A[i]$を複数ある減少列のパイル$P_j$のいずれかに積み上げる
- Step 2: 減少列パイルの最上部の値$top(P_j)$から最小値を順番に取り出し出力する
Step 1, 2の詳細を順番に説明していきます。
Patience Sorting Step 1
説明の都合上、減少列パイル$P_j$は横に並べるものとして初期状態では減少列パイルは1つもないものとします。
- $A$を左から右へ順番に読み込み以下の基準で$A[i]$を減少列パイル$P_j$に積み上げる
- $A[i]<top(P_j)$なる最左のパイル$P_j$に積み上げる
- もしそのようなパイル$P_j$がなければ一番右に新しい空の減少列パイル$P_j$を作成し、そこに$A[i]$を積み上げる
動作例を具体例を見ながら見ていきましょう。
$A[1]=7$を読み込みました。
パイルが1つもないので、新しいパイル$P_1$を作成して$A[1]=7$を積み上げます。
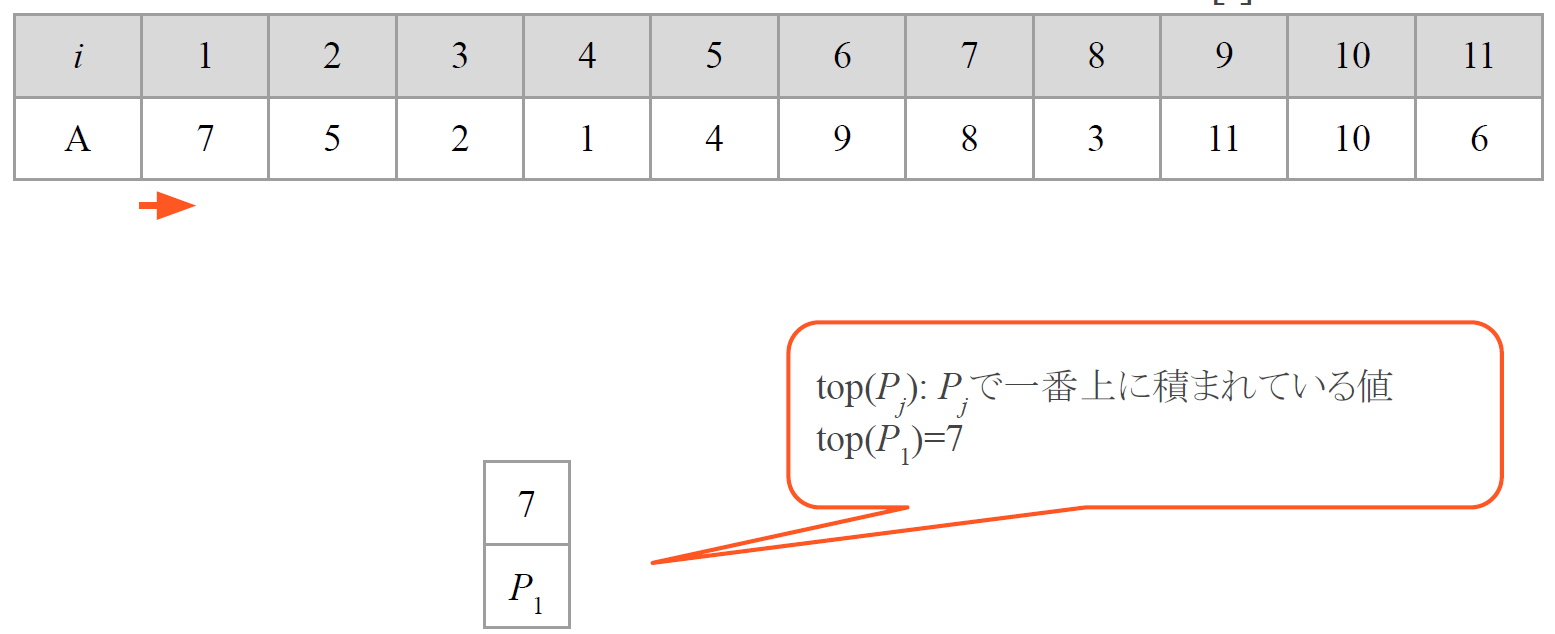
$A[1\ldots 4]=(7, 5, 2, 1)$は減少列なのですべて$P_1$に積まれました。
$A[5]=4$は$top(P_1)=1$よりも大きいため、$P_1$に積み上げられません。
新しいパイル$P_2$を作成して$A[5]=4$を積み上げます。
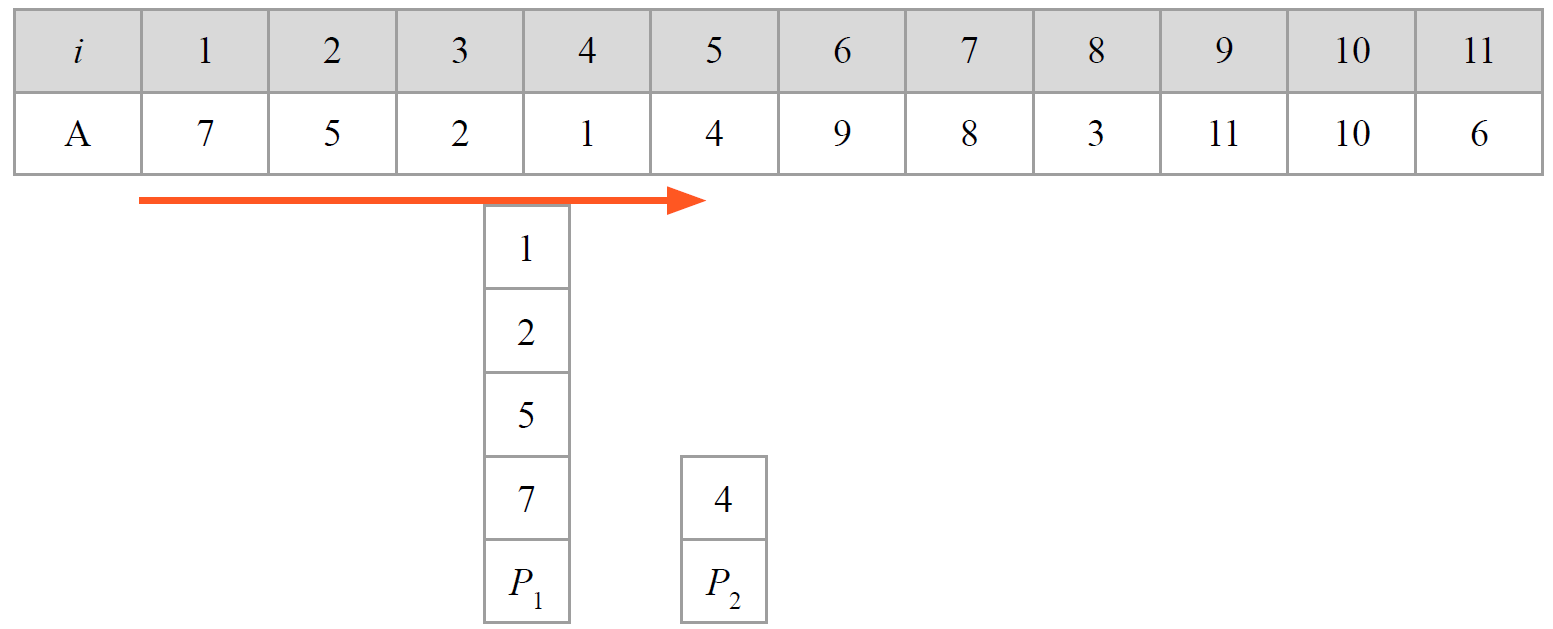
すべて読み込むと以下のようなパイル$P_1, \ldots, P_4$が出来上がりました。
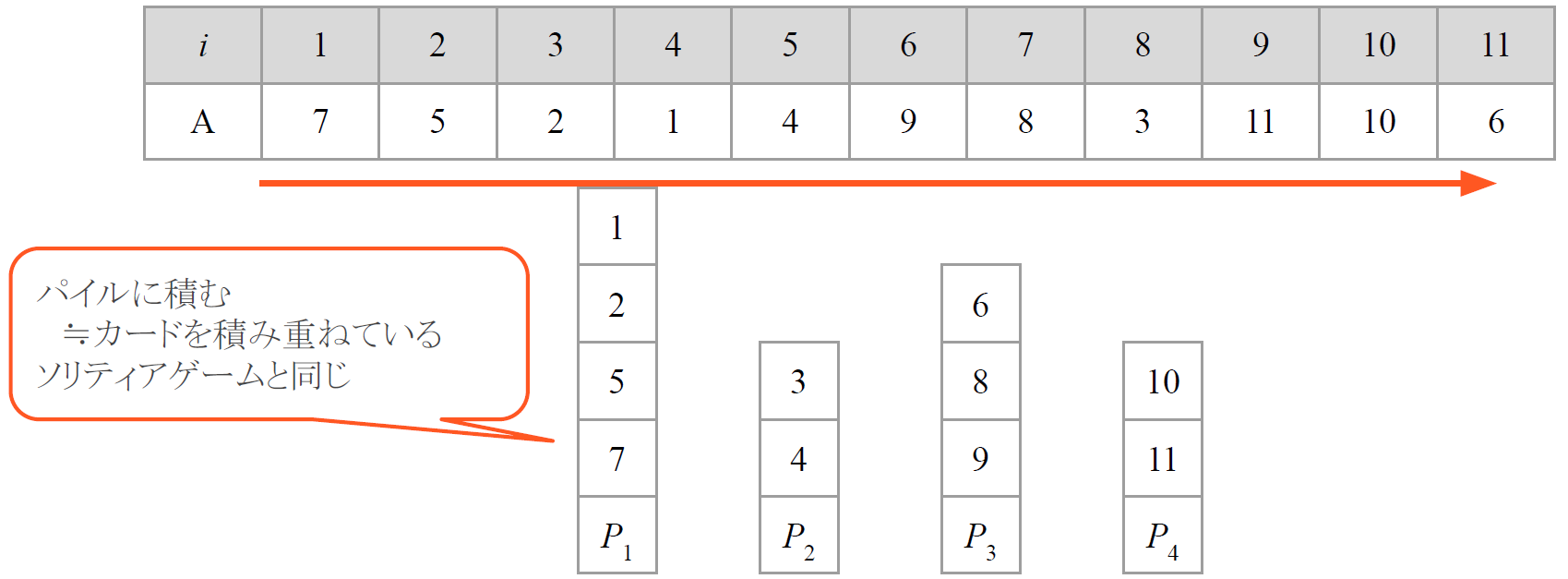
これでStep 1は終了です。
Patience Sorting Step 2
Step 2の詳細は以下のようになります。
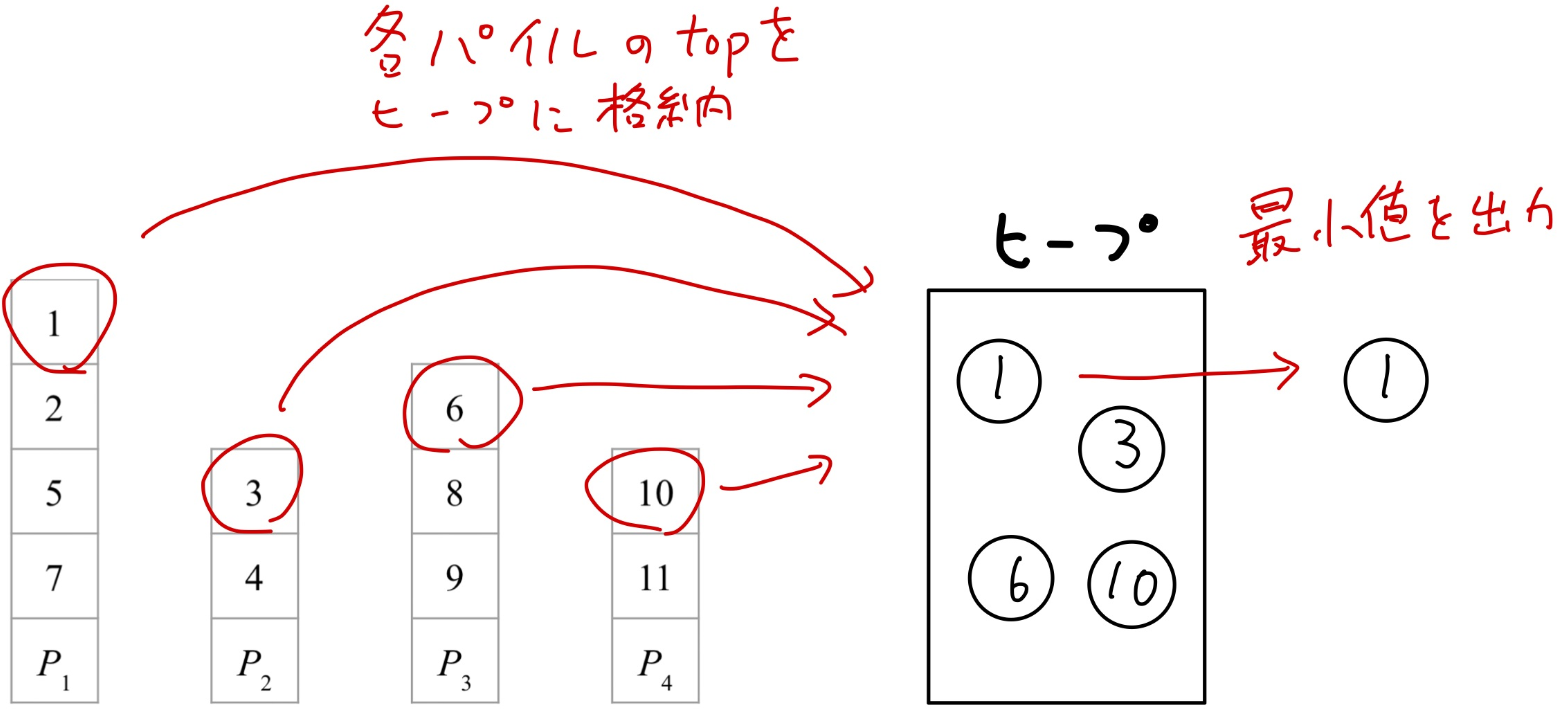
- Step 1で作成した各パイルのtopの値をコピーしてヒープ構造に格納する
- 補足:ヒープ構造は最小値を効率的に取り出すことが出来るデータ構造です。
- ヒープ構造から最小値を取り出し、ソートの結果として出力する
- ヒープから取り出した値を、パイルから取り除き、新しいtopの値をヒープに格納する
- 上記の処理をパイルがすべてからになるまで繰り返す
Step 2も同様に動作例を見ていきましょう。
各パイルのtop、$1, 3, 6, 10$をヒープ構造に格納します。
(ヒープ構造は本質ではないので詳細は書いていません)
ヒープから最小値である$1$を配列$A$の最小値として出力します。
取り出した$1$をパイル$P_1$から取り除き、次の$P_1$のtopである$2$をヒープに格納します。
ヒープから最小値である$2$を$A$の$2$番目に小さい値として出力します。
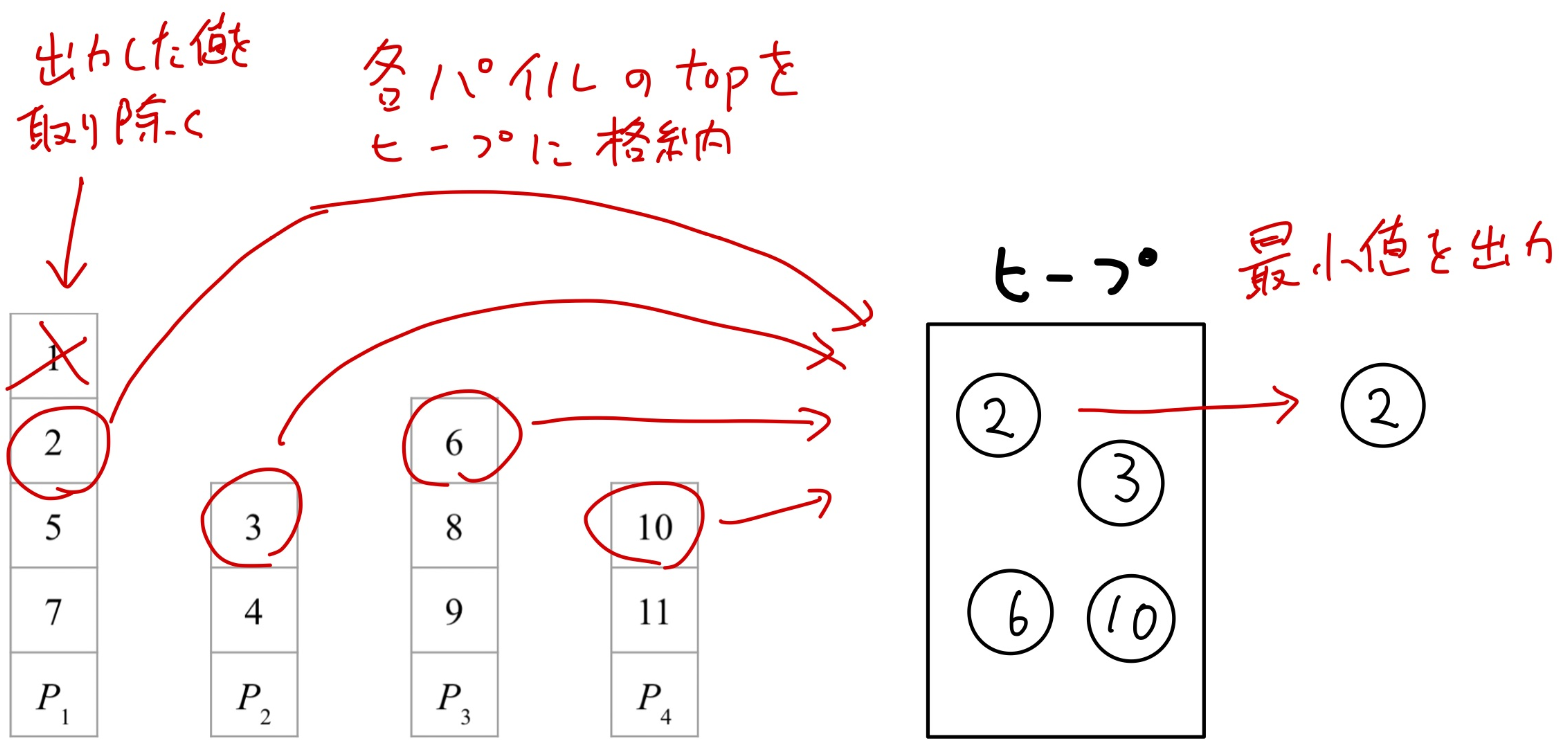
上記を繰り返すことで、$A$のソートした値を順番に出力します。
計算の正しさ
Patience Sortingは以下の性質により、正しくソートした値を出力します。
- すべての$A[i]$はいずれかのパイルに積まれている
- 各パイルはtopが小さくなるように減少列になっている
- 上記より$A$の最小値はパイルのtopのいずれかとなる
- 上記の性質は$A$の最小値を取り除いても成り立つ
計算時間
まずStep 1の計算時間から考えていきましょう。
アルゴリズムは以下の性質が成り立つようにパイル列に$A[i]$を積んでいきます。
| パイル列の性質 |
|---|
| パイルtop列は$top(P_1)<top(P_2)<\cdots$と昇順にソートされている |
そのため、パイル数の最大数を$P$とすると、挿入位置はパイルtop列上で二分探索し$O(\log P)$時間で計算できます。
これを$n$個の要素について行うため、アルゴリズム全体では$O(n \log P)$時間で計算可能です。
Step 2ではヒープには高々$P$個の要素を格納します。
ヒープは要素1つあたり、格納、取り出しを$O(\log P)$時間で計算できます。
$n$個の要素についてヒープへ格納、取り出しを行うので、$O(n \log P)$時間で計算可能です。
以上より、Patience Sortingは全体で$O(n \log P)$時間でソートを行います。
最悪時には$P=n$となり、$O(n \log n)$時間となりますが、一番良いときは$P=1$となり$O(n)$時間でソートを行います。
最長増加列問題
最長増加列問題は入力配列の中に出現する最長の増加列を求める問題です。
例えば以下の配列には、$(2)$、$(2, 4, 8)$、$(1, 4, 8, 10)$などの増加列が出現し、$(1, 4, 8, 10)$のような長さ4の増加列が最長となります。

最長の増加列は複数ある場合がありますが、それらのうち1つを答えればOKです。
Patience Sortingを使った最長増加列の計算
Patience SortingのStep 1に次の一手間をかけるだけで簡単に最長増加列を計算することが出来ます。
$A[i]$をパイル$P_j$に積み上げるときに、$A[i]$から一つ前のパイル$P_j$のtop、$top(P_{j-1})$へのリンクを記憶する
この一手間を加え、第一段階が終了したあと最後のパイルの任意の要素からリンクをたどった値を出力します。
出力した値は必ず最長増加列となります(証明は後述)。
具体例を見てみましょう。
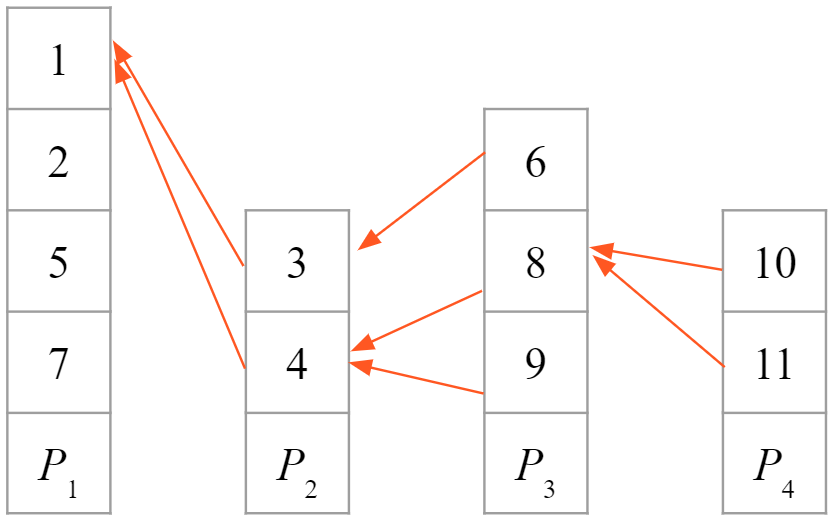
Patience Sortingの説明でも使った以下の例では次のようなリンクが作成されます。

$P_2$の$4$から$P_1$の$1$へのリンクに着目してみましょう。
$A[1\ldots 4]=(7, 5, 2, 1)$は減少列ですべて$P_1$へ積まれます。
その次に$A[5]=4$は$P_1$には積めないため、あたらしく$P_2$を作成し積み、そのときの1つ手前のパイルのtop、$top(P_1)=1$へのリンクを作成します。
その他のリンクについても同様の基準で作成されています。
それでは次に$P_4$の要素を見てみましょう。
$P_4$の2つの要素どちらでも良いのですが、ここでは$10$に着目してみましょう。
$10$のリンクをたどって得られる、$(10, 8, 4, 1)$は配列$A$では先頭から$(1, 4, 8, 10)$の順で出現する増加列になります。
配列$A$には長さ$5$以上の増加列は出現しないのでこの増加列が配列$A$の最長増加列となります。
計算の正しさ
それではこのアルゴリズムが正しく最長増加列を出力していることを検証していきましょう。
2つの補題を証明することで計算の正しさを保証できます。
| 補題 1 |
|---|
| Patience Sortingで作られたパイル数を$P$、$A$の任意の増加列を$\mathit{IS}=(A[i_1], A[i_2], \dots)$とすると、$P\geq | \mathit{IS}|$が成り立つ |
証明
$P<\mathit{IS}$なる増加列があったと仮定して、$\mathit{IS}$の各要素がPatience Sortingのパイル列ではどこに格納されているかを考えます。
$\mathit{IS}$のサイズは$P$を超えているわけなので、少なくともどこか1つのパイルでは$\mathit{IS}$の要素が2つ以上格納されているはずです。
ここで各パイルは$A$に出現する減少列を表していることを思い出しましょう。
つまりこの$2$つの要素は減少列を表し、$\mathit{IS}$が増加列であることに矛盾します。
以上より、補題が成り立ちます。
| 補題 2 |
|---|
| Patience Sortingで作られたパイル数を$P$、$A$の任意の最長増加列を$\mathit{LIS}=(A[i_1], A[i_2], \dots)$とすると、$P\leq | \mathit{LIS}|$が成り立つ |
証明
アルゴリズムが長さ$P$の増加列を出力することを示します。
Patience Sortingはパイル列のtopがソートされるように要素を積んでいきます。
ですので$A[i]$をパイル$P_j$に積んだとき、そのリンク先との値には$top(P_{j-1})<A[i]$の関係が成り立ち、$top(P_{j-1})$は配列$A$上で$A[i]$よりも前に出現している、つまり増加列になることが保証されます。
そのため、最後のパイルからたどった値は$A$上の長さ$P$の増加列を表します。
よって最長の増加列は$P$以上となります。
補題1と2により、任意の増加列は長さ$P$以下であり、かつ最長の増加列は長さ$P$以上となるため、最長の増加列の長さは$P$となり、アルゴリズムの出力は最長増加列であることが保証されます。
おわりに
本記事ではソリティア風の動作をするPatience Sortingの紹介を行いました。
ソリティアゲームを遊ぶときにはPatience Sortingのことを思い出してあげて下さい(?)。