| 問題 |
|---|
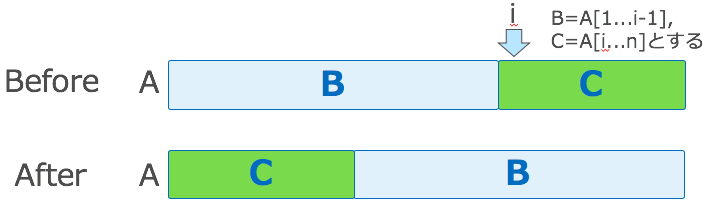
| 配列$A[1...n]$と位置$i$が与えられたとき$A$をローテションさせた$A[i...n]A[1...(i-1)]$を線形時間で作れ、但し使える領域は$A$と定数個のポインタ(つまりin-place)、使用可能な操作は$swap(i, j)$: $A[i]$と$A[j]$の入れ替えのみとする。 |
難易度的には優しく解法もたくさんあり頭の体操レベルかと思います。何人かの知り合いに出題して傾向をみると、「こうすれば解けそう」というアイディアは結構すぐ思いつくようですが、正当性を説明することがなかなか難しいようです。
正当性とは以下の2点です。
- 操作は正しいか?(正しくローテションされているか?)
- 線形時間で動作するか?
正当性を説明することはとても重要です。この問題について取り組むときには、アルゴリズムとその正当性の説明もセットで考えてみてください。
これは答えがすぐ見えないための画像です。自力で解きたい方はここで一旦考えてみてください。

解法1
それでは解法を見ていきましょう。
はい、単純ですね。そしてこの解法を思いついた人が一番多いのではないでしょうか。
それでは正当性について考えていきましょう。
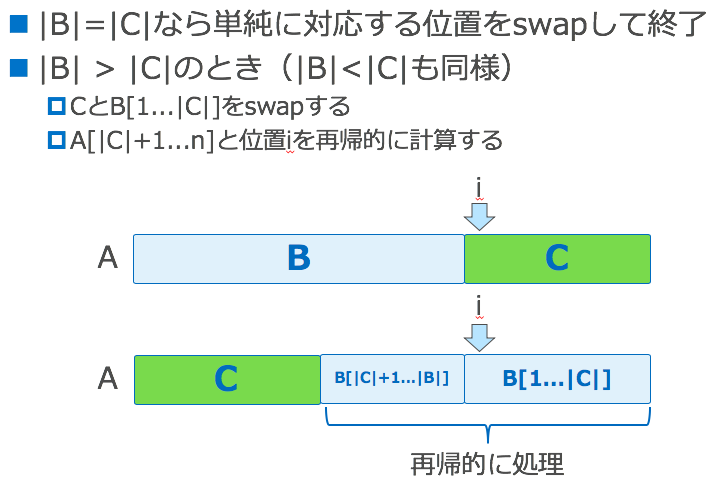
まず$|B|=|C|$について考えると、この操作で$B$も$C$も正しい位置に保存され、swap回数も$|B|$回だけですので、ポイント1、2について正当性が言えることが分かるかと思います。
それでは$|B|>|C|$の場合を考えてみましょう($|B|<|C|$はその逆なので略します)。
正しくローテション出来ているか
- $C$の位置は最終状態の正しい位置に保存されますので、$C$に関しては正しくローテションされます
- $B$に関してはローテションが必要なので、同様に再帰的に処理を行います
- 上記2つより全体のローテションが正しく行われます(問題サイズは単調減少ですのできちんと停止します)
線形時間で動作しているか
- 再帰処理の各ステップで必要なswap回数は$|C|$回
- $C$は最終状態の位置にあり、その後の再起ステップではswapされない
- よってswap回数は高々出力配列のサイズ$|A|$回となる
はい、スッキリですね。
では解法2に移っていきましょう!
解法2
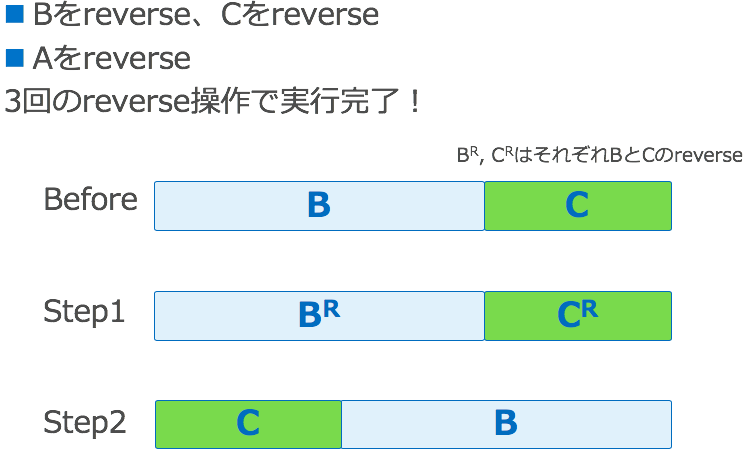
解法2は定数回のreverse操作のみで配列のローテションを行います。配列$A[1...n]$をreverseするとは$A^R=A[n]A[n-1]...A[1]$を作る操作です。$A$のreverse操作は左端、右端から等距離にある$A[i]$と$A[n-i+1]$をswapすることにより線形時間でin-placeに実行可能です。
興味がある方はここで一旦読むのをやめて、reverse操作のみでローテションを行う方法を考えてみてください。
それでは解法を見ていきましょう。
Step1の状態でA全体をreverseすると、後方の$C^R$がreverseされて$C$が前方に、前方の$B^R$がreverseされて$B$が後方に移動され、最終的にStep2の状態になります。
この方法のすごいところは単純かつ正当性が一目瞭然なところです。素晴らしいですね。
おわりに
どうですか?問題は単純ですが、色々な解き方がありなかなか面白い問題ではないでしょうか?
in-place計算は可能な計算が限られており、パズル的な発想で解く方法がとても多く、個人的に気に入っているタイプの問題です。
最後に面白そうなin-placeな問題を出題して終わりにしたいと思います。
| 問題 |
|---|
| ソート済みの配列$B[1...n]$と$C[1...n]$が配列$A$に連続して$A=BC$の形式で保存されています。線形時間でin-placeに$A$を安定ソートしてください。 |

この問題はローテーションほど簡単ではないですが、いくつか仮定(配列の長さ、安定の条件をなくす)をおいていけば難易度は下がっていきますので、ぜひ取り組んでみてください。ちなみにこれが出来るとマージソートが$O(n \log n)$時間でin-placeに実行可能になります。
安定でないバージョンは[Practical In-Place Merging, Huang and Langston, 1994]の論文でシンプルに解かれていますので気になる方は参照してみてください。