はじめに
この記事は、CTF チーム zer0pts で行った yoshi-camp にて用いた発表資料に加筆・修正をしたものです。また、この資料の内容を基に同様のタイトルで魔女のお茶会 2021/冬にて発表を行いました。
この資料では、最短経路問題について実践的な視点より演習を交えながら解説をします。全体の大まかな流れとしては、
- 最短経路問題の定義とアルゴリズムを確認する
- 例題と共に最短経路問題への定式化の手順を確認する
-
ShortestPathライブラリを用いた実装を学ぶ - 定式化のテクニック(困難な定式化やインスタンスの高速化)を学ぶ
- ヒューリスティックな高速化を学ぶ
となります。これによって最短経路問題だと認識できる問題を増やし、それらを容易に実装できるようになることで最短経路問題を武器としてもらうことを目標としています。
3 章は独自ライブラリによる実装を扱っているので、アルゴリズムのみに興味がある場合は読み飛ばしてしまって全く問題ありません。また、4 章と 5 章は内容としてはほぼ独立なので、好きな順番で読んで頂いて構いません。
例題について
この記事には、数問の問題が例題として含まれます。それぞれの問題について、このフォルダの problems/q[n].py に問題のジェネレータが、problems/a[n].py に想定解のコードが入っています。
1. 基本
問題の定義
まず、最短経路問題の定義を確認しておきましょう。
二頂点対最短経路問題
「状態 $A$ から状態 $B$ に正のコスト $c$ で遷移できる」のような関係がいくつかある時に状態 $S$ から状態 $T$ まで遷移できるかを判定し、できるならばそのための最小コストを求める。
一般的な最短経路問題はグラフの上で定義されることが多いですが、今回は陽にグラフを与えないこととしました。このように定義することによって、考察上や実装上での利点があります。グラフを陽に考えないことによって、状態や関係といった抽象的な概念が出てきました1。具体例を基に、定義を確認しましょう。
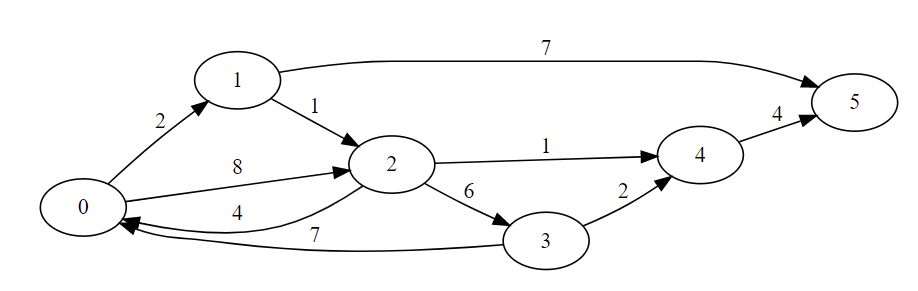
以下のような図を考えます。丸は街を表しているとしましょう。また、街 i から街 j への番号 c が書かれた矢印は、街 i と j が距離 c の一方通行の道で繋がれていることを示しています。このとき、「街 0 から街 5 まで移動するための最短距離はどれだけか?」という問題は最短経路問題となります2。
この問題を上の定義に従って考えてみると、状態はどの街に居るか、関係は可能な街から街への移動となります。上の定義に当てはめ、成立することを確かめてみてください。
アルゴリズム
前項では、基本的な最短経路問題の定義を確認しました。次に、これを解くアルゴリズムを見ていきます。そのために、最短経路問題の種類を 2 つ紹介しておきます。
単一始点最短経路問題
状態 $S$ から到達できる全ての状態について、$S$ から遷移するための最小コストを求める。
全点対最短経路問題
全ての状態間について、遷移できるかを判定し、できるならばそのための最小コストを求める。
これらの問題は、考える頂点対の集合が異なるだけで本質的には同一です。ではなぜ敢えて定義したのでしょうか。それは、単純に下位互換の問題を解くアルゴリズムを繰り返し適用するよりも、特化したアルゴリズムを用いることで効率が良くなりうるからです。
単一始点最短経路問題
では、それぞれの問題について解くアルゴリズムを紹介していきます。まずは二頂点対間最短経路問題を解くアルゴリズム3を……と言いたいところですがこれはせず、単一始点最短経路問題を解くアルゴリズムから紹介します。なぜならば、後者を解くアルゴリズムが前者を解くにも十分に高速で有用だからです。
単一始点最短経路問題のためのアルゴリズムとしては、古くから知られている Dijkstra 法というものがあります。これは、状態 $S$ から到達できる状態数を $V$ 、到達できる遷移の数を $E$ としたとき、時間計算量 $O(E\log V)$4 で動作します。
全点対最短経路問題
次に、全点対最短経路問題を解くアルゴリズムを紹介します。これについても、古くから知られている Warshall-Floyd 法というものがあります。これは、全状態数を $V$ としたとき、時間計算量 $O(V^3)$5 で動作します。なお、全点から Dijkstra 法をしたとしても $O(VE\log V)\subset O(V^3\log V)$ ($\because E\in O(V^2)$) となるため、速度がクリティカルになる場面でない限りは Dijkstra 法で事足ります。後述のライブラリでも、オプションで使用するようにしています。
経路復元
ここまでは、最短コストのみを求めるという話をしてきました。しかし、実際には最短コストを与える方法のほうが重要になってくる場合が多いです。便利なことに、ほとんどの最短経路問題を解くアルゴリズムは、それを与える遷移の列も同時に求めることができます。よって、以降では明記することなく具体的な遷移方法も求まっているものとします。
2. 最短経路問題の考え方
前章では、最短経路問題は状態間の遷移について扱うものであるということを強調して説明しました。これは、最短経路問題としての解釈を行う際に大切な考え方だからです。最短経路問題によって解ける問題は、必ずしも経路の距離を求めるような見た目をしているとは限りません。最短経路問題を距離を求める問題だと捉えていると、そうでない問題を最短経路問題だと解釈できなくなってしまいます。この章では、最短経路問題として問題を解く際の手順を具体例と共に追っていきます。
問題における「状態」を考える
最短経路問題として問題を捉える際、状態のとり方を考える必要があります。多くは、問題で考えている状態そのものを当てはめてしまって問題ありません。その状態を用いて正しく問題を解けるかどうかは、以下の条件を満たしているかで概ね確認できます。
- 遷移を定めるために十分な情報を持っているか
- その状態から遷移が一意に定まるか?
- 状態が問題を正しく表せているか
- 考慮が漏れている情報はないか?
では、以下の問題を例に考えてみましょう。
問題 1
以下の操作は、全て $\bmod 256$ 上で考える。
整数 $0\le X\le 255$ があり、
(a) $X\leftarrow X+d$ ($0\le d\le 5$)
(b) $X\leftarrow 2X+d$ ($0\le d\le 5$)
の操作ができる。
(a) はコスト 2 で、(b) はコスト 8 で行える。$X$ を $0\le Y\le 255$ にするための最小コストを求めよ。
この例では、問題で考えている主要な状態は現在の $X$ のみです6。なので、これを状態にすれば良さそうです。これについて、上で挙げた事項が満たされているかを確かめてみましょう。まずは、「遷移を定めるために十分な情報を持っているか」についてです。遷移についてはまだ考えていませんが、後述する通りこれは満たされています。次に、「状態が問題を正しく表せているか」についてです。これを完璧に確かめるのは難しいですが、今回のような単純な問題であれば満たされていることは簡単に確認できます。
状態からの遷移を考える
次に、先に挙げた状態からどのような遷移が定まるのかを考えてみましょう。今回の場合は「操作」として明示的に $X$ を変化させる方法が与えられているので、それを遷移とすれば良さそうです。ですから、$X$ からは $X+0, X+1, \cdots, X+5$ へコスト 2、$2X+0, 2X+1,\cdots,2X+5$ へコスト 8 での遷移があることが分かります。この状態と遷移の取り方によって、先に挙げた問題は最短経路問題として解釈できたことになります。
今回は、状態を取る際に遷移のことをを考慮しませんでした。しかし、状態の取り方に問題があるために上手く遷移が取れないということも起こりえます。慣れてきたら、状態の取り方を考える際に遷移のことも考慮してみるようにしましょう。
計算量を見積もる
ここまでは、問題を最短経路問題として捉える方法のみを追ってきました。最後に、その最短経路問題を解くことが現実的を考えましょう。解くことが現実的でない場合のほとんどは、時間的な制約によるものです。時間的に現実的かを判断するために役に立つのが、計算量による実行時間の見積もりです。
計算量とは、アルゴリズムが終了するまでに行う基礎的な処理7の総数を入力を引数として表した関数のことです。処理の総数を厳密に求めるのは骨が折れるので、計算量はしばしば $O$ 記法によって表されます。$O$ 記法とは関数の漸近的な挙動を表すためのもので、$x$ が十分大きければ $g(x)$ が $f(x)$ にほぼ比例することを $g(x)\in O(f(x))$ と表します8。この記法では、関数にかかる定数倍や支配的でない項は無視されます。ですから、計算量から処理回数を見積もる際には定数倍を考慮しないといけません。定数倍は実装にもよりますが、特別なもの9でなければ数十倍程度に収まると考えて良いでしょう。
処理回数を見積もれたら、それがどの程度の時間で実行できるかを考えます。現代のコンピュータでは、一秒に $10^9$ 回程度の処理を実行できます。しかし、これは命令レベルでの話です。Python など中間言語方式の言語では、インタプリタの性能による実行時間の悪化も発生します。参考までに、C と Python のインタプリタ毎の空ループの実行速度を以下に挙げます。
| 操作数 | C++(gcc) | PyPy | CPython |
|---|---|---|---|
| $10^5 \approx 2^{17}$ | 一瞬 | 一瞬 | 一瞬 |
| $10^8 \approx 2^{27}$ | 100 ms | 100 ms | 2 sec |
| $10^9 \approx 2^{30}$ | 1.5 sec | 1.5 sec | 25 sec |
JIT コンパイルのある PyPy はネイティブバイナリと遜色ない性能を発揮している一方、中間言語のインタプリタである CPython では 20 倍ほどの定数倍が実行時間にかかっていることが分かると思います。この CPython の結果を基に、今後は $10^8$ 回を一秒間に実行できる操作数の目安とすることにします。
これらの情報を基に、上で扱った問題がどの程度の時間で解けるのかを推定してみます10。Dijkstra 法の計算量は以下の通りでした。
状態 $S$ から到達できる状態数を $V$、到達できる遷移の数を $E$ としたとき、時間計算量は $O(E\log V)$
$V$ はあり得る全状態数である 256 とします。到達できる状態数はもう少し少ないかもしれませんが11、ここでは大まかに評価してしまいましょう。各状態から 6 個の遷移があるので、到達できる遷移数 $E$ は $6\cdot V$ より 1536 個となります。よって、アルゴリズムの持つ定数倍を 10 倍程度とすると、総処理数は $1536 \log 256 \cdot 10 \approx 2000\cdot 8\cdot 10 = 160000$ 回程度と分かります12。これを操作数の目安と照らし合わせると、1 ミリ秒程度で解けるはずであると概算できました。
上の問題を一般化して考えてみましょう。
問題 1'
以下の操作は、全て $\bmod M$ 上で考える。
整数 $0\le X< M$ があり、
(a) $X\leftarrow X+d$ ($0\le d\le D$)
(b) $X\leftarrow 2X+d$ ($0\le d\le D$)
の操作ができる。
(a) はコスト 2 で、(b) はコスト 8 で行える。$X$ を $0\le Y< M$ にするための最小コストを求めよ。
この問題で、$M$ の値を変化させることを考えます。このとき、以上の情報から推測できる $D$ の値と解ける時間の関係は以下のようになります。
| $d=2^{0}$ | $d=2^{4}$ | $d=2^{8}$ | $d=2^{12}$ | $d=2^{16}$ | |
|---|---|---|---|---|---|
| $n=2^{8}$ | 0 msec | 3 msec | 52 msec | 838 msec | 13421 msec |
| $n=2^{16}$ | 104 msec | 1677 msec | 26843 msec | 429 sec | 114 min |
| $n=2^{24}$ | 40265 msec | 644 sec | 171 min | 45 h | 30 day |
実際に、次の章の実装で計測をしてみました。定数倍のズレはありますが、おおよそ予測の範囲に収まっていることが分かります。
| $d=2^{0}$ | $d=2^{4}$ | $d=2^{8}$ | $d=2^{12}$ | $d=2^{16}$ | |
|---|---|---|---|---|---|
| $n=2^{8}$ | 0 ms | 2 ms | 26 ms | 448 ms | 6203 ms |
| $n=2^{16}$ | 357 ms | 700 ms | 8433 ms | 100+ sec | 100+ sec |
| $n=2^{24}$ | 100+ sec | 100+ sec | 100+ sec | 100+ sec | 100+ sec |
また、PyPy を用いた結果は以下の通りでした。以前の単純なループの実験ではバイナリと遜色ない結果を残せていましたが、今回は 5 倍程度の高速化に収まっていますね。
| $d=2^{0}$ | $d=2^{4}$ | $d=2^{8}$ | $d=2^{12}$ | $d=2^{16}$ | |
|---|---|---|---|---|---|
| $n=2^{8}$ | 0 ms | 1 ms | 6 ms | 93 ms | 1586 ms |
| $n=2^{16}$ | 79 ms | 160 ms | 1959 ms | 100+ sec | 100+ sec |
| $n=2^{24}$ | 18527 ms | 100+ sec | 100+ sec | 100+ sec | 100+ sec |
3. 実装
上で挙げた例題について、ptrlib の ShortestPath クラスを利用して実装してみましょう。ShortestPath クラスではいくつかのアルゴリズム13を使用できますが、デフォルトは Dijkstra 法が使用されます。
ShortestPath のコンストラクタは、引数に遷移関数を取ります。遷移関数は引数に状態を取り、(次の状態, 遷移コスト, 遷移の識別子) をイテレータとして返す必要があります。これは、遷移関数が yield を用いて実装されることを想定した設計です。遷移の識別子は最適な遷移を復元した際に使われるものなので、復元が必要ない場合は None 等の適当な値で問題ありません。また、状態の型は hashable である、つまり dict のキーとして使えるものである必要があります。つまり、複数の変数を状態としたい場合は list 型ではなく tuple 型を使用する必要があります。
試しに、上の問題の遷移関数を実装して ShortestPath のインスタンスを作ってみましょう。今回は、状態は int 型で持つのが良いでしょう。遷移は (a), (b) それぞれ d が 0 から 5 までの 6 種類あります。これを実装すると、以下のようになります。
COST_A = 2
COST_B = 8
N = 256
def transition(state):
for i in range(6):
yield ((state + i) % N, COST_A, f"A{i}")
yield ((state * 2 + i) % N, COST_B, f"B{i}")
sp = ShortestPath(transition)
構築した ShortestPath は、インデクサに始点をキーとして渡すことで dict ライクなオブジェクトを返します。このオブジェクトに対して同様に終点を渡すことで (最小コスト, {value: それを与える経路の配列}) を返します。つまり、上の例では sp[s][t] とすることで s-t 間最短路を求めることができるということです。なお、存在しないキーを渡した際に例外は返さず、結果として (inf14, {value: raise Exception()}) を返します。
よって、上の例において到達コストとそれを与える経路を求めるコードは以下のようになります。
X = 20
Y = 120
cost, path = sp[X][Y]
print(f'cost: {cost}')
print(f'path: {path.value}')
計算コスト
アルゴリズムの実行は、デフォルトでは終点のキーにアクセスした際に動的に行われます。つまり、sp[s] が実行された時点では実際の計算は行われていません15。また、経路のリストは value プロパティにアクセスされた際に初めて計算されます。よって、リストを愚直に連結することによる計算量の悪化は起きていません。
演習
以下に、最短経路問題として解くことができる問題を挙げます。2 章で扱った考え方を基に考察し、計算量を見積もった後に実装をしてみてください。
問題 2 (基礎)
長さ $1\le N\le 10$ の数列がある。これを 2 つの数を入れ替えることを繰り返して昇順に並び替えたい。2 つの数を入れ替えるためには、入れ替える 2 つの数の積だけコストを支払わなければいけない。昇順に並び替えるために必要な最小のコストを求めよ。
問題 3 (発展)
使えるキーが $K \subset {0, 1, 2, \cdots, 9}$ のみである電卓に $\bmod M$ ($M \le 10^{5}$) で $R$($0\le R \lt M$) となる数を打ち込みたい。このようなことが可能であるかを判定し、可能ならば最小何桁で達成できるかを求めよ。
4. 定式化の際のテクニック
以上では、愚直に状態と遷移を取ることで十分高速に最短経路問題を解くアルゴリズムを適用できる問題を扱ってきました。しかし、状態の取り方が上手く行かなかったり、状態数が多すぎることで現実的には解けないような問題となってしまうこともあります。この章では、
- 状態の数が多すぎて現実的に解けない
- 上手く最短経路問題として解釈ができない
- 遷移の数が多すぎて現実的に解けない
といったケースについての対処法を学びます。
状態を纏める
現実的に解くことができない最短経路問題を解ける形にするための一つの手法として、到達可能な状態数を減らすことがあります。ここで、「Dijkstra 法のボトルネックは遷移数で、状態数でないのでは?」と思うかもしれません。実際、状態数を減らしても遷移数が減らないならば、状態数を減らす意味はほぼないと言ってよいでしょう。ただ、多くの場合は状態数の削減は遷移数の削減に繋がることが多いです。
状態数を減らせるシチュエーションとして最も多いのは、区別しなくてよい状態が別の状態として残っている場合です。これは、「状態が無駄な情報を持っている」とも言い換えられます。一つ例を見てみましょう。
問題 4
石の山が $N\le100$ 山ある。山 $i$ には石が $0\le A_i\le3$ 個積まれている。残りの石の数の合計が $S$ のとき、一つの山から $1$ 個以上 $B_S$ 個以下の石を取ることができる。
最小何手で全ての石を取ることができるか?
これを最短経路問題として表すことを考えます。状態として石の山を持つと、遷移は各山から石を何個か取るコスト 1 の操作となります。
このとき、取りうる状態数は $O(4^N)$ 個となっています。起こりうる遷移数ももちろん同等のオーダーになっているので、このままでは高速に解くことができません。ここで、状態が持つ無駄な情報について考えてみます。
少し考えると、この問題は「石が $i$ 個の山が $C_i$ 個ある」という状態のみで解くことができます。つまり、山の順序が無駄な情報となっていたのです。順序の情報を取り去った後のあり得る状態数は $O(N^3)$ 個であり16、各状態からの遷移も高々 3 種類と十分少ないため、この状態の取り方による最短経路問題は高速に解くことができます。
状態に情報を追加する
上では、最短経路問題として解釈した後の計算量削減について学びました。では、最短経路問題としての解釈が難しい場合はどうでしょうか?
状態の取り方の際に気をつけるべきことは、以下の通りでした。
- 遷移を定めるために十分な情報を持っているか
- その状態から遷移が一意に定まるか?
- 状態が問題を正しく表せているか
- 考慮が漏れている情報はないか?
今までは、問題から自明に分かる状態のみを考えてきました。しかし、そうではないものも存在します。
問題 5
街が $N \le 100000$ 個あり、 $M \le 200000$ 本の道路がある。$i$ 番目の道路は街 $A_i$, $B_i$ を相互に結んでいて、通過に $c_i$ 分かかる。道路は必ず決められた経過時間ちょうどで通過しなければいけない。道路の途中で立ち止まったり、折り返したりすることはできないが、街では整数時間だけ留まることができる。
また、いくつかの街には制約がある。$j$ 個目の制約は、現在時刻が $5n+t_j-0.5$ から $5n+t_j+0.5$ ($n$ は任意の整数)の間、街 $D_j$ に存在していると命を失ってしまうことを表している。
時刻 $0$ に街 $0$ から出発した時、街 $N-1$ に命を失わずに到着できる最も早い時刻は何時か。なお、この問題で与えられるパラメータは全て整数である。
この問題を見た際に、状態としては「街 $T$ にいる」というものが思いつくと思います。しかし、今回の場合はそれでは不十分です。なぜならば、時刻 1 に街 1 にいることと時刻 2 に街 1 にいることが同じ状態に含まれているからです。
では、どのような状態を取ればよいでしょうか。ここで、状態に複数の変数を含めることを考えます。頂点にいる現在時刻を持たせれば、上であげた状況を区別することができますね。しかし、今度は状態数が $N\cdot N\cdot\max(c_i)$ 個と膨れ上がってしまいました。
前項の通り、区別しなければいけない情報は何かということを考えると、今回の場合は「今の時刻 $\bmod 5$」のみであるということが分かります。こうすると、値の組 $(T, q)$ によって「街 $T$ に時刻 $5n+q$ でいる」という状態を持てることとなります。終了状態が $(N-1, 0), \cdots , (N-1, 4)$ と複数個てきてしまっていますが、これについては全ての結果のうち最も良いものを採用すれば問題ありません。
このように複数の変数を状態に持たせられるようになると、表現できる状態の幅がかなり広がります。ぜひとも使いこなせるようになっておきましょう。
無駄な遷移を削減する
この章の始めでは、状態数を削減することによって間接的に遷移数を削減しました。しかし、遷移について直接削減を考えることがあります。
遷移の削減はアドホックなものが多く、難しくなる傾向があります。そのため、ここでは例を挙げるに留め、詳細には立ち入らないことにします。
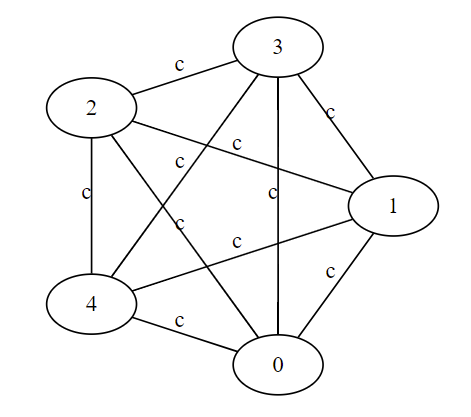
例1. 完全グラフ
以下のような、全頂点から他の全頂点へと辺があるようなグラフを完全グラフと呼びます(簡便のため、無向グラフとして表しています)。このようなグラフでは頂点数 $N$ に対して $O(N^2)$ の辺ができてしまうため、辺数が膨れ上がってしまいます。
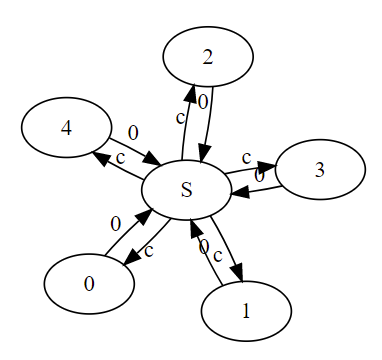
このようなグラフに対して、特殊な頂点を一つ付け足すことで辺の数を削減することができます17。
このような状況は、「ワープが可能」といった設定で出てくることが多い印象です。
例2. 推移的なグラフ
以下のような、辺 $(a, b, c_{a,b})$ かつ $(b, c, c_{b,c})$ が存在するならば $(a, c, c_{a,c})$ も存在し、$c_{a,b}+c_{b,c}=c_{a,c}$ であるという条件を満たすようなグラフを考えます。これも上と同様に、辺の数が二乗のオーダーで膨れ上がってしまいます。
これについては、これ以上複数の辺の結合として表せない極小な辺のみを残しても等価となることが分かります。
演習
問題 6 (JOI2019/2020 二次予選 D - テンキー改題)
あなたは今、電卓の 0 のキーを指差している。一回の操作で、
- 一つ大きな番号のキーに指す先を移す(指が 9 を指している場合は 0 に移るものとする)
- 今指しているキーを押す
ことの何れかができる。
今、$\bmod M$ ($M \le 10^{5}$) で $R$($0\le R \lt M$) となる数を打ち込みたい。このようなことが可能であるかを判定し、可能ならば最小何桁で達成できるかを求めよ。
問題 7 (巡回セールスマン問題の亜種)
$N$($N\le 16$) 個の街を $M$ 本の道が繋いでいる。$i$ 本目の道は、街 $s_i$ と街 $t_i$ を距離 $c_i$ で繋いでおり、双方向に行き来可能である。街 0 から始まり全ての街を訪れるような経路のうち、最短のものの長さを求めよ。なお、同じ街を何度訪れても良く、最後に街 0 に戻ってこなくても良い。
5. ヒューリスティックな高速化
前章では、計算量をオーダーレベルで改善するための手法を見てきました。しかし、実世界ではそう上手くもいかないこともあります。そのように役に立つのが、ヒューリスティックな最適化です。ヒューリスティックな最適化の一つに、枝刈りがあります18。枝刈りとは、目標状態に到達できないような状態を判定し、そこからの探索を行わないようにする処理のことです。
最短経路問題に適用できるヒューリスティックな手法として、現在状態から目標状態までの推定コストを用いた Dijkstra 法の最適化があります。この最適化には、A* アルゴリズムという名前がついています。このアルゴリズムの力を体感できる例として、15 パズルを見てみましょう。
15 パズルを ShortestPath ライブラリを用いて解くコードは、以下の通りです。
ds = [-4, -1, 1, 4]
puzzle = (4, 1, 2, 3, 5, 6, 10, 7, 8, 13, 14, 9, 12, 11, 15, 0)
goal = (*range(16),)
init = tuple(puzzle)
def transition(state):
pos = state.index(0)
for d in ds:
swappos = pos + d
if 0 <= swappos < 16:
l = list(state)
l[pos], l[swappos] = l[swappos], l[pos]
yield (tuple(l), 1, (pos, swappos))
sp = ShortestPath(transition)
cost, path = sp[init][goal]
これの実行にはおよそ 20 秒ほどかかりました。ここで、「それぞれのパズルのピースの目的地までの距離の和」を評価関数として A* アルゴリズムで高速化を図ってみます。なお、この評価関数は、毎回距離を 1 縮められた場合の理論的な最小コストを表しています。
A* アルゴリズムは ShortestPath ライブラリに実装されています。これを使うには、以下のように cost_estimator 名前付き引数に state から dest までのコストを返す関数を渡せば良いです。
...
def estimator(state, dest):
assert(dest == goal)
cost = 0
for i in range(1, len(state)):
i1, j1 = i // 4, i % 4
i2, j2 = state[i] // 4, state[i] % 4
cost += abs(i1 - i2) + abs(j1 - j2)
return cost
sp = ShortestPath(transition, cost_estimator=estimator)
cost, path = sp[init][goal]
これの実行は 0.7 秒ほどで終了しました。A* アルゴリズムが効果的に動いていることが分かると思います。
なお、A* アルゴリズムで用いる推定関数は解までのコストの下界を与えるものであると良いです。この条件を満たす場合、得られる解が常に最適解となるからです。
-
分かる人のために言うと、これらはグラフでの定義における頂点と辺に対応しています。 ↩
-
というより、一般的にはこの問題を基として最短経路問題が定義されている場合がほとんどです。 ↩
-
あまりこの問題には明るくないですが、簡単なものでは双方向 Dijkstra 法等が知られています。最悪計算量をオーダーレベルで改善するものではありませんが、定数倍高速化が見込めるようです。 ↩
-
フィボナッチヒープという特殊なヒープを用いると $O(M+N\log N)$ になります。私感ですが、フィボナッチヒープは一般的に使われるヒープと比較した際に同じ操作では低速なために現実的なインスタンスではクリティカルな改善にはならず、あまり使われていない気がします。 ↩
-
Warshall-Floyd 法よりも高速なアルゴリズムは幾つか知られていますが、$O(V^{3-\epsilon})$ のアルゴリズムは現在のところ知られていません。これが存在するかは未解決問題となっています。 ↩
-
無理やりこじつければ「現在までにかかったコスト」なども状態とすることができますが、これによって起こりうる遷移が変化することはありません。よって(後に詳述しますが)「現在までにかかったコスト」は冗長な情報となり、状態に含めても意味がありません。 ↩
-
計算量を考える際には計算モデルというものを定め、どのような処理を基礎的なものとするかを定めます。主に固定長整数の加減乗除と比較/分岐、そしてビット演算が基礎的な処理とされることが多いです。 ↩
-
厳密には、関数 $f$ に対してある定数 $c$ が存在し、十分大きな $x$ に対して常に $g(x)< cf(x)$ を満たすことを表します。 ↩
-
例えば、行列行列積を計算する Strassen のアルゴリズムの計算量は(次元を $N$ として) $O(N^{2.81})$ ですが、$N=100$ 程度までは愚直な $O(N^3)$ よりも高速になりません。 ↩
-
実は、この問題にはより効率的な解法があります。しかし、今回はあくまでも最短経路問題を用いて解くことを考えることとします。 ↩
-
少し考えると、256 個全てに到達できることが分かります。 ↩
-
ここで、log の底は 2 としています。底を変化させても定数倍の差にしかならないため、計算量解析では適当な値を使ってしまうことが多いです。 ↩
-
Dijkstra 法と前述の Warshall-Floyd 法、Dijkstra 法をヒューリスティックに高速化した A* 法が実装されている。 ↩
-
返される
infの値はコンストラクタのinfinity引数によって変更できます。コストとして独自の数値クラスを用いる場合に有用です。 ↩ -
ShortestPathクラスが用いるアルゴリズムによって異なる可能性があります。現状実装されているdijkstra,floydwarshall, そしてastarアルゴリズムでは全てこのように計算されますが、今後もそうであるとは限りません。 ↩ -
順序の情報を取り去った後の状態は、$N$ 個の区別できない山を個数に対応する 4 グループに分割することで得られます。これは $N$ 個の山と 3 個の仕切りを一列に並べることと一対一で対応する。これは $_{N+3}C_3\in O(N^3)$ 個となり、上の評価が得られます。 ↩
-
このような頂点のことを「超頂点」などと呼んだりします。 ↩
-
もちろん、うまい枝刈りがオーダーレベルでの高速化に繋がることもあります。 ↩