ポアソン分布と二項分布

#ポアソン分布 (Poisson distribution)
単位時間あたりに平均 λ 回ランダムに起こる現象が、単位時間にk 回起きる確率を表すのに使われる確率分布がポアソン分布である。Po(λ) と表現され、確率質量関数は以下で与えられる。
　$\begin{eqnarray*}f(x)=\frac{e^{-\lambda}\lambda^x}{x!}\end{eqnarray*}$

#電話の例
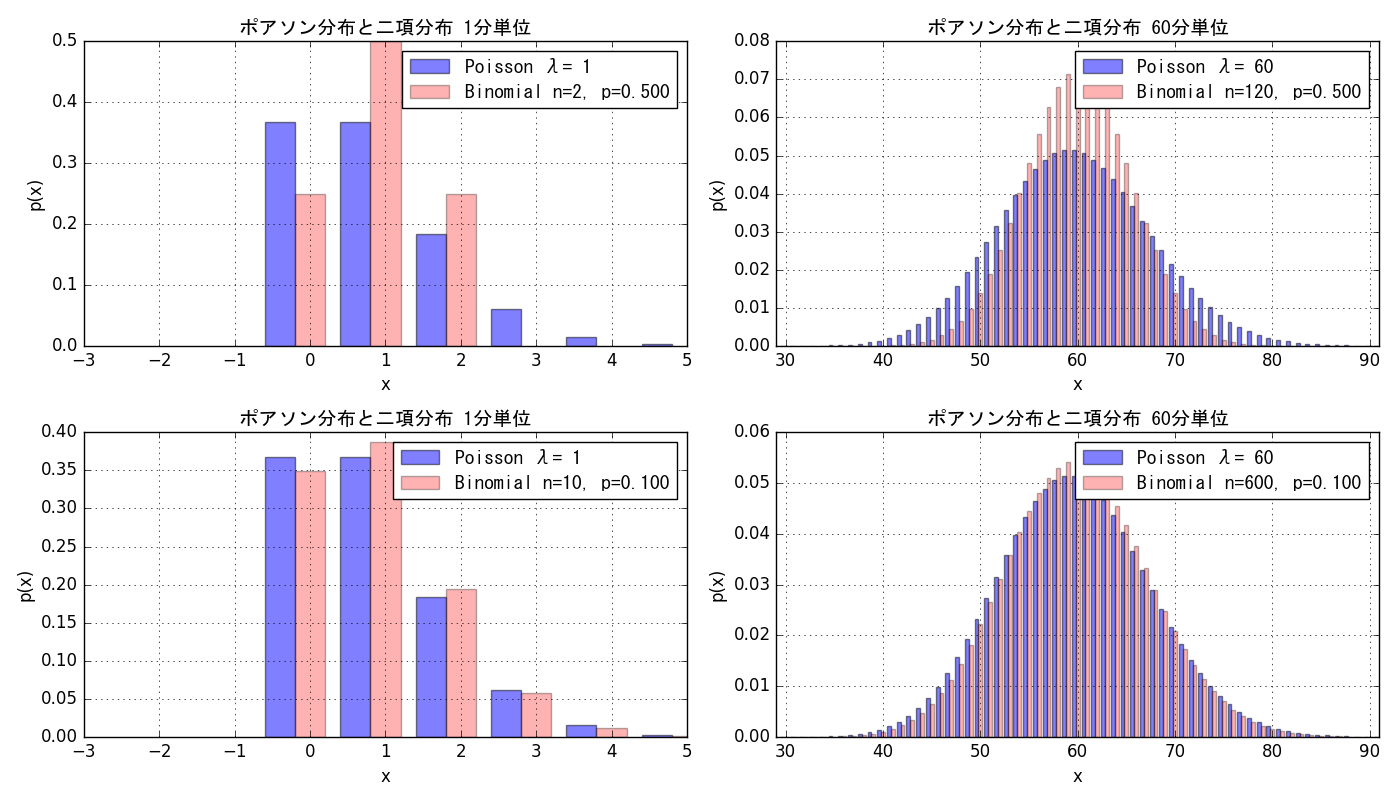
1分間に1回、つまり1時間に60回電話がかかって来る会社があるとする。1分間または1時間にx回電話がかかって来る確率はどの程度のものだろうか。二項分布と共にポアソン分布をpythonでグラフ表示してみる。

ポアソン分布と二項分布

import datetime
print(str(datetime.datetime.now() ) + " 開始" )
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sct
from scipy.misc import comb     # comb()は組み合わせを計算する関数
#日本語を使う場合はフォントを準備
from matplotlib.font_manager import FontProperties
fp = FontProperties(fname='C:\WINDOWS\Fonts\msgothic.ttc', size=14)


def poisson_pmf(k, lamb):
    ret= np.e**(-lamb)
    for i in range(k):
        ret *= lamb / (i + 1)
    return ret


plt.figure(num=1,figsize=(14,8))
j = 0
#二項分布の1分単位の試行回数。[2]なら30秒間を1回の試行として電話の事象の有無を確認する。
for n_count in [2,10]:
    p=1/n_count #1回の試行で電話の事象が起こる確率　λ=np

    #1分単位なら1回電話がかかってくるのでλ=1(回)、60分単位ならλ=60(回)
    for lam in [1,60]:
        j += 1
        n=n_count * lam

        #ポアソン分布
        x_poi = np.arange(0,100)
        y_poi=[poisson_pmf(k, lam) for k in x_poi]
        #y_poi=sct.poisson.pmf(x,lam)
        #二項分布:n回ベルヌーイ試行を繰り返してその確率を計算。試行の計算は内包表記。
        x_bin = np.arange(0,n+1)
        y_bin=[comb(n, z)*p**z*(1-p)**(n-z) for z in x_bin]

        plt.subplot(2,2,j)
        plt.xlabel('x')
        plt.ylabel('p(x)')
        plt.title("ポアソン分布と二項分布 %d分単位" %(lam), fontproperties=fp)
        plt.xlim(lam-lam**0.5*4,lam+lam**0.5*4) #範囲制限
        #ポアソンの棒グラフは左側にずらして表示する
        plt.bar(x_poi-0.4, y_poi, align="center", width=0.4, color="blue"
                ,alpha=0.5, label="Poisson λ= %d" % lam)
        plt.bar(x_bin,     y_bin, align="center", width=0.4, color="red"
                ,alpha=0.3, label="Binomial n=%d, p=%.3f" %(n,p) )
        plt.legend(loc="best", prop=fp)    #凡例を表示
        plt.grid(True)

plt.tight_layout()#一部が出力画像からはみ出る場合にグラフの位置サイズを調整
plt.savefig('figure.png')
print(str(datetime.datetime.now() ) + " 終了" )
plt.show()

4つのどのグラフも、1分間に1回の頻度で電話が掛かってくる事を仮定している。ただし右列のグラフの単位は1時間である。
上段のグラフは、30秒間中に電話がかかる確率を0.5として二項分布を描いている。下段のグラフは、6秒間中に電話がかかる確率を0.01として二項分布を描いている。
まれに発生する事象がポアソン分布の対象になると言われる事があるが、グラフ右列の電話コールの例の様に、単位時間あたり60回も発生するランダムな事象でも、ポアソン分布に従う。
二項分布における試行回数nが大きく確率pが小さいとき、二項分布からポアソン分布を導く事ができる為、「まれに発生する事象」という表現が使われる事が多いのだろう。