#フーリエ級数展開(Fourier Series)
フーリエ変換(Fourier Transform)とはなんでしょうか.理系の人なら,信号処理論に限らずどこかで必ず遭遇していると思います.
特に,直感的なイメージがしにくい複素数表記に重きを置いて,まずはフーリエ級数展開(Fourier Series)から解説をしていこうと思います.
後に続くフーリエ変換(Fourier Transform),離散時間フーリエ変換(Discrete Time Fourier Transform),離散フーリエ変換(Discrete Fourier Transform)もこれを順々に発展させていけば理解できるので,まずはフーリエ級数展開の意味をしっかりと理解しましょう.
##フーリエ級数展開の意味
といっても,やってること自体はいたってシンプルです.一言で表すと,周期関数を三角関数の重ね合わせに分解しているということです.
マクローリン展開やテイラー展開というのを習ったと思います.あれは,関数を$x, x^2,..., x^k$といった「べき」で展開しようとするものでした.フーリエ級数展開は,「べき」ではなくて三角関数$\cos(\omega_0 t), \cos(2\omega_0 t),...,\cos(k\omega_0 t)$に分解していこうとするものです.($\omega_0=\frac{2\pi}{T_0}$であり,これは基本各周波数と呼ばれるやつです.)
式の形を見たほうが分かりやすいかもしれません.
$$f(t) = a_0 + \sum_{k=1}^{+\infty} \bigl\{ a_k\cos(k\omega_0 t) + b_k\sin(k\omega_0 t)\bigr\}$$
一つ目の$a_0$は定常成分と呼ばれ,信号全体の上下を決める成分なので前に出しています1.残りの項は全て$\sin$波と$\cos$波に分解できていることが分かります.視覚的なイメージは下図で,ある周期関数(Periodic function) $f(t)$が三角関数に分解できていることが分かります2.

一つ例を見てみましょう.
$$f(t)=t$$
という簡単な関数を三角関数に分解していこうと思います.
結果だけ先に言うと,以下のような式にフーリエ級数展開できます.
$$f(t)=\sum_{k=1}^{+\infty} \frac{2}{k} (-1)^{k+1}\sin(kt)$$
この形だと難しく見えるかもしれませんが,
$$f(t)= 2\sin(t)-\sin(2t)+\frac{2}{3} \sin(3t)-...$$
と続くということです.
これが本当に $f(t)=t$ になっているのかを見てみましょう.
下のアニメーションは,$k=1,2,3,5,10,20,50,100$と増やしていったときのグラフの形を表しています.つまり,上の式の項を段々と増やしていったときの挙動を表しています.

$k$を増やせば増やすほど $f(t)=t$ にフィッティングできていることが分かりますよね.$k\rightarrow +\infty$ まで足し合わせていけば $f(t)=t$ に出来そうなイメージが湧いたでしょうか.
あらゆる周期関数が三角関数の重ね合わせで表現できるイメージが湧きましたか.直線や,複雑な曲線でも基本的な三角関数に分解できるのって何だか不思議だし,とても面白いですよね.
でも,ただ面白いだけではないんです.工学的に様々な利点があります.
##フーリエ級数展開のモチベーション##
一つには,周波数というものが見えてくるという利点があります.
$\sin(k\omega_0 t)$ という信号は,周波数$k\omega_0$ をもつ信号ですが,それがどれだけ含まれているかは$b_k$というフーリエ係数(Fourier coefficient)を見れば分かります.$k$を横軸にとって$b_k$を縦軸にプロットすれば,どの周波数がどれだけ含まれているかが一目でわかるようになるのです.例えばさっきの例では,$\sin(t)$の係数は$2$,$\sin(2t)$の係数は$-1$,$\sin(3t)$の係数は$\frac{2}{3}$ であるので,それを下の図のようにプロットしていきます.

これが周波数スペクトル(Frequency spectrum) と呼ばれるもので,「ある信号をスペクトル分解して・・・」と言っていたのはこの作業をしていたことなんですね.
スペクトル解析というのは,実に色んな分野で使われています.例えば,太陽の元素構成が分かったのもこのスペクトル解析のおかげなのです.「太陽は主に水素とヘリウムで構成され・・・」なんて言われますが,何故それが分かったか疑問に思ったことはないでしょうか.実際に太陽に行って調べたなんてことはまさかありませんよね.実は,太陽光をスペクトル解析することで分かったのです.原子は,エネルギー状態が変わるときに電磁波を放出するのですが,その周波数は原子の種類によって決まっています.ですから太陽光を周波数分解して対応する原子を見つけていけば,どの原子がどのくらい含まれるかが分かるのです.
もう一つのメリットは,三角関数というものが微分をしても形が変わらないということです.いやいや,確かに$\sin(t)$を微分すれ$\cos(t)$に,$\cos(t)$を微分すれば$-\sin(t)$に,なるのですが三角関数であることは変わりません.これらは複素数表示すると$e^{jt}$とかにまとめられるわけですが,この形ならば微分をしても$je^{jt}$となるわけですから変わらないわけです.すぐ後に複素フーリエ級数展開というのにまとめるわけですが,そのモチベーションの一つにこのことがあります.
これは,微分方程式を解くときに便利なわけです.微分の前後で形が変わらないことによって,微分方程式が代数方程式にできます.
そういえば,LTIシステムというのは線形微分方程式で書けるんでしたよね.そうです,だからLTIシステムを解く上でも非常に便利なわけです.これだけだと何を言っているのか分からないと思うので,詳しくは[周波数応答と固有関数]の記事を見てください.
##フーリエ級数展開の複素数表記
フーリエ級数展開とは,周期関数を三角関数の重ね合わせで表すものでした.だから上の式が直感的に理解しやすいです.
しかし大抵の教科書や講義ではここでは止まらず,上の式をこねくり回して複素フーリエ級数展開
$$f(t) = \sum_{-\infty}^{+\infty} c_ke^{j\omega_0 kt}$$
というのを導出してくると思います.
導出過程は省略しますが,ただオイラーの公式に当てはめるだけなので式展開を追えば理解はできるし,さっきの式に比べたら簡潔にかけているのでこっちの方が良さげだなと思うのですがイマイチしっくり来ません.
そこで今回は,そのモチベーションや意味について深く見ていこうと思います.
###フーリエ級数展開の形をちょっと変えてみる
まず初めに,フーリエ級数展開の意味を理解し直すところから入りましょう.(じゃあ最初からこう説明しろよという声が聞こえそうですが$\cdots$)
普通のフーリエ級数展開の式は
$$f(t) = a_0 + \sum_{k=1}^{+\infty} \bigl\{ a_k\cos(\omega_0 kt) + b_k\sin(\omega_0 kt)\bigr\}$$
のように書けました.$\sin$と$\cos$の重ね合わせは頑張れば$\cos$に合成できることを思い出すと次のように書けます.
$$f(t) =\sum_{k=0}^{+\infty} a_k\cos(\omega_0 kt + \theta_k)$$
ここで,$a_k$は振幅(amplitude),$\theta_k$は初期位相(initial phase)を表すことは分かると思います.
つまり,フーリエ級数展開とは,ある振幅とある初期位相を持った$\cos$波に分解することだったのです.(三角関数と聞けばまず$\sin$を思い浮かべるのか,フーリエ級数展開とは$\sin$波に分解することだと思っている人が多いですが(かつての僕もそうでした),本質的には$\cos$波に分解することだと思っておいた方がいいです.上の式は$\sin$に合成することもできるので数学的に間違っているわけではないですが,後に述べる初期位相のことを考えると$\cos$波だと理解した方が理にかなっています.)
一番初めの表記では,全てを初期位相0の$\sin$波と$\cos$波に分解することにしましたが,ここでは全てをcos波で分解することにした代わりに,初期位相という情報を新たに付与しなければならなくなったのです.どちらにせよ $(a_k, b_k), (a_k, \theta_k)$ という二変数を使って表さなくてはいけないところは変わりません.
###改めて複素数表記
フーリエ級数展開が$\cos$波の重ね合わせだと理解し直したところで,改めて複素数表記を見てみましょう.
$$f(t) = \sum_{-\infty}^{+\infty} c_ke^{j\omega_0 kt}$$
さっきの表記とは異なってるように見えますが,本質的には$\cos$波への分解を表しているということを理解していきます.
####螺旋に分解
まず、導出過程は忘れて,この式単体に注目しましょう.
この式の言わんとするところは,「$f(t)$がexponentialの重ね合わせに分解できる」ということです.
exponentialとはどんなグラフかといえば,それは以下のような螺旋になります.

つまり,$f(t)$はこのような螺旋に分解できるということです.
しかしここで多くの人は虚数部分の存在に疑問を持つと思います.もともと分解する前の関数は実関数だから,虚部が出てくるって変ですよね.
分解ができるということは,それを合成すれば元に戻るということです.
つまり,合成したときに虚数部分がうまくキャンセリングしてくれればいいのです.($2$を、$(1+j)+(1-j)$に分解したっていいのと同じです.)
このことを見ていきましょう.これを理解する上で大事になってくるのが,負の周波数と、**$c_k$というフーリエ係数(Fourier coefficient)**です.
####負の角周波数
$$f(t) =\sum_{k=0}^{+\infty} a_k\cos(\omega_0 kt + \theta_k)$$
$$f(t) = \sum_{-\infty}^{+\infty} c_ke^{j\omega_0 kt}$$
この二つの式の大きな違いとして,kのサメーションが0から始まっていたのに対し,$-\infty$から始まるようになっているということです.つまり,$\cos$に分解したときは正の周波数成分だけだったのが,exponentialに分解するときには$-3\omega_0$のような負の周波数成分も出てきてしまうということです.
負の周波数とは何でしょうか.
周波数の物理的意味は,「単位時間あたりに繰り返される振動の数」ですから,負の周波数とは「1秒間に振動が負の回数繰り返される」となって何のこっちゃ分かりません.
ですから,グラフを見てイメージを持たせましょう.
$e^{j\omega_0 kt}$とは$t$に従って反時計回りを描いていきますが,e$^{-j\omega_0 kt}$は時計回りを描いていきます.つまり,下図のようにその正のexponentialとは逆回りを描きながら進む螺旋のことなのですね.

####フーリエ係数(Fourier coefficient)
フーリエ係数(Fourier coefficient)とは,各周波数成分についている係数$c_k$のことです.(今後は螺旋のことを,「ある周波数を持った$f(t)$の構成成分」という意味で「周波数成分」と呼んでいきます.)
この係数は各周波数成分に対応してついており,その周波数成分の特徴を表すものとなっています.
では,その特徴とはなんでしょうか.$\cos$波に分解したときのことを思い出してもらうと分かると思いますが,振幅と初期位相でしたね.
まず,振幅はどうでしょう.
$$|c_ke^{j\omega_0 kt}|=|c_k|$$
と書けることから,$c_k$の絶対値が各周波数成分の振幅を表していることが分かると思います.これは今までと変わらないのでイメージしやすいですよね.各周波数成分の$c_k$倍が$f(t)$に含まれている訳ですから,振幅は$|c_k|$になりそうです.
では,初期位相はどうでしょう.
初期位相とは,「初期つまり時刻0での位相」のことです.ですから,$t=0$を代入して,
$$\arg \bigl(c_ke^{j\omega_0 k0}\bigr) =\arg c_k$$
となります.つまり,$c_k$の偏角が各周波数成分の初期位相を表しているのです.
これら2つからもう分かったと思いますが,フーリエ係数とは,その周波数成分の振幅と初期位相を情報として持ったものと言えるわけです.
嬉しいのが,一変数に,しかも絶対値と偏角という分かりやすい形で含まれていることです.さっきまで二変数使わなければならなかったことを考えると驚くべき進歩ですよね.
さあ、ここまででフーリエ係数の意味が分かったところで、フーリエ係数には非常に重要な性質があります。それが下のような性質です。(この性質は、複素数表記の導出過程から簡単に示せます。)
\left\{
\begin{array}{ll}
|c_k| = |c_{-k}|\\
\arg c_k = -\arg c_{-k}
\end{array}
\right.
つまり,各周波数成分の正負のペアは,絶対値が等しく初期位相が符合反転であるということです.要は共役(conjugate)ということですね.
もう一度確認しますが,フーリエ係数の絶対値と偏角は,それぞれその周波数成分の振幅と初期位相を表したものでした.
ですからこの関係式は,「正負のペアの螺旋は,同じ半径で,正負が丁度逆のスタート地点から,逆回りに螺旋を描いていく」ということを意味します.イメージとしては下図です.
この縛りがあるおかげで,どの時刻でも,二つの複素数ベクトルは常に共役の関係になります.

ですから、その正負の周波数成分を足し合わせると虚部はきれいに消えて、実部だけに$\cos$波が表れるのです。

$\sin$波への分解ではなく,$\cos$波への分解だと考えた方がいいと言った心はここにあります.上の図をよく見てもらえば分かると思いますが,初期位相が0の場合($\arg c_k = 0 \Rightarrow c_k$が実数)実軸上からスタートするので,デフォルトは$\cos$波なのです.
結局$\cos$波への分解と本質的に変わらないということが理解できたでしょうか?
要は,$\cos$波をさらに螺旋二つに分解していたのですね.
こうすることのメリットはたくさんあって,まずは式が簡潔に書けることがあります.
それから,実数の範囲では振幅と初期位相を$(a_k, \theta_k)$という二変数を使って表さなくてはいけなかったのが,複素数に拡張したことで$c_k$という一変数で表せるようになっています.絶対値と偏角という分かりやすい形で組み込まれているということも素晴らしい点です.
そして,少し上でも触れましたが,各成分$c_ke^{j\omega_0 kt}$は微分をしても形が変わらないようになっています.微分方程式を解くのに非常に扱いやすい形だということです.だから、複雑な関数を微分方程式に代入して解く場合でも、まずは個々の周波数成分に分解してから個別に微分方程式に代入して最後に足し合わせれば,簡単に解くことができるのではないかというイメージが湧くと思います.(もちろん,このように分解してから足し合わせるのが許されるのは,微分方程式が線形であるとき,つまり線形微分方程式に限ります.)
これが,「微分方程式を周波数領域で見て,代数的に解く」と言われるやつです.(僕は大学の講義でこの言葉を最初に聞いたときにさっぱり理解できませんでした。) 何度も言いますが,詳しくは[この記事]に書いています.
###補足
- フーリエ係数のグラフでは,一般的には$k<0$の部分,つまり負の周波数の部分を書かずに正の部分のみを表記します.これは,
\left\{
\begin{array}{ll}
|c_k| = |c_{-k}|\\
\arg c_k = -\arg c_{-k}
\end{array}
\right.
という条件が分かっているので,正の周波数だけ書けば自然と負の周波数の情報は分かるからです.決して,負の周波数が存在しないという訳ではないことに注意しましょう.
-
また,正の周波数のフーリエ係数の絶対値を見て,その周波数の$\cos$波がその絶対値で含まれているのだ思い込んではいけません.上で確認したように,正と負のペアによって$\cos$波が完成するからです.その$\cos$波の振幅は$2|c_k|$となります.
もちろん$e^{j\omega_0 kt}$という成分の振幅は$|c_k|$なのですが,周波数$\omega_0 k$の$\cos$波としては$2|c_k|$になります.(まあ工学的には,他の周波数成分に比べてどれくらい大きいかという相対的な値が分かればいいので,あまり拘らなくてもいいポイントではあるのかもしれません.そのため,わざわざ平方根を取らなくてはいけない$|c_k|$ではなくて,$|c_k|^2$を計算してパワースペクトラムと言ったりします.) -
さらに,
\left\{
\begin{array}{ll}
|c_k| = |c_{-k}|\\
\arg c_k = -\arg c_{-k}
\end{array}
\right.
という縛りは,$f(t)$が実関数であるときに限るということに注意しましょう.正負のペアを足し合わせて虚部のみがキャンセリングする条件なのですから当たり前ですよね.
逆に,$f(t)$が純虚数関数のときはどうなるでしょうか.上で考えたように,二つのベクトルがどのような関係にあれば実部がうまくキャンセリングされて虚部だけが残るのでしょうか.
より理解が深まると思うのでぜひ考えてみてください.答えは[この記事]に書いてあるので,こちらも参照してください.
#フーリエ変換(Fourier Transform)
ここまでフーリエ級数展開の説明をしました.しかし,しれっと「周期関数を」という枕詞をつけていたことに気づいたでしょうか.
実は,最初に出した例
$$f(t)=\sum_{k=1}^{+\infty} \frac{2}{k} (-1)^{k+1}\sin(kt)$$
はあたかも$f(t)=t$を完璧に再現できているように示しましたが,

その表示幅を広げてみてみると,実は以下のようになっていたのです.

つまり,これは周期$2\pi$の周期関数になってしまっているというです.裏を返すと,フーリエ級数展開というものは周期性を仮定しないと使えないのです.
しかし,これでは困りますよね.世の中の信号というものは周期的でないものの方が圧倒的に多いのですから.周期的ではない関数についても使えるようにとフーリエ級数展開を拡張していくのはごく自然な流れだと思います.
このように,フーリエ級数展開を非周期関数にまで拡張したものがフーリエ変換(Fourier Transform)になります3.
大概の教科書では,フーリエ級数展開の式を式変形していって,以下のような式を導出してくると思います.ここではその過程は省きますが,さほど難しくはありません.
上がフーリエ変換で,下が逆フーリエ変換の式です.
$$X(\omega) = \int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt$$
$$f(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}X(\omega)e^{j\omega t}dt$$
ただ,大事なのは根本的にはフーリエ級数展開と同じことをやっているということです.周期的ではない一般的な関数についても,それを周波数成分(螺旋)の重ね合わせで表現しようとしているだけなのです.
下の二式(下がフーリエ級数展開の式で,上がフーリエ級数を求める式です)と同じ形をしていることが分かると思います.
$$c_k = \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)e^{-j\omega_0 kt}$$
$$f(t) = \sum_{-\infty}^{+\infty} c_ke^{j\omega_0 kt}$$
フーリエ級数展開からフーリエ変換の式の違いは,
- フーリエ変換の積分区間が無限になっていること
- 逆フーリエ変換が級数ではなく積分になっていること
ぐらいです.
一つ目に関しては問題ないと思います.そもそもフーリエ変換がそのように定義したものなのですから.
二つ目も,物理的には同じことを言っています.周波数成分を重ね合わせて時間関数を復元しているということを表していることに過ぎません.ただ,級数と積分の違いですから(そしてこれが重要な変化なのですが),周波数スペクトルが連続的になるということを意味しています.
下の周波数スペクトルは,最初に例に出したように $f(t)=t$ という関数を[$-\pi, \pi$]でフーリエ級数展開したときの周波数スペクトルです.これは見ての通り離散的なものです.
しかし,一般的にフーリエ変換の場合は,このようなグラフではなく連続的になるということです.

ここからは自分へのメモ書きですが,数式に基づいた自分なりのイメージを書きます.
- プロットの通り,周波数関数をフーリエ級数展開したときの周波数スペクトル(すなわちフーリエ級数のプロット)の値は,有限の値を持っています.しかし,同じ関数をフーリエ級数展開ではなくて,フーリエ変換したときには,その値にデルタ関数が掛け合わされた値に発散します.これは式をちゃんと計算するとそうなります.(周期関数を無理矢理フーリエ変換したら,デルタ関数が出てくるということです.元々1周期しか積分しなかったものを無限の積分区間で積分するのですから,無限大に発散するのは当然の話ですよね)
- また,上のプロットの値は,基本周波数を間隔として並んでいます.フーリエ変換は,周期を無限と考えて積分するものですから,裏を返せば基本周波数は$\frac{1}{\infty}$とすることに相当します.つまり上のプロットの各値の間隔が極限まで狭まっていくイメージです.
すなわち,デルタ列がどんどんと狭まっていくイメージです.デルタ関数はその場で面積を持つ関数4なので,高校数学で積分を考えたときの微小な短冊だと思えばよくて,これらが近づいていくと,やがて級数から積分に,離散的な点列から連続的なグラフになることはイメージできると思います.
これが,フーリエ変換の周波数スペクトルが連続値になる直感的なイメージです.
これはかなりガバガバな説明です.数式を用いた説明は[離散性と周期性]の記事で詳しくまとめようと思います.
よくある誤解
最後に初学者にありがちな誤解を指摘しておきますが,フーリエ変換とは,(フーリエ級数展開における)**フーリエ係数を求める部分に相当しています.**そのフーリエ係数を使って,「はいはい,この周波数成分はこれだけの大きさを持ってるのね,えっと,次の周波数成分は$\cdots$」として$x(t)$を再構成していくのがフーリエ級数展開です.つまりこっちは逆フーリエ変換に相当します.周波数領域での情報を使って,時間領域の$f(t)$を再構成するということです.その対応づけを分かりやすくするために,上記の式の比較はその順番で書きました.
フーリエ変換によって,信号を時間領域(Time domain)から周波数領域(Frequency domain)に写像します.逆フーリエ変換によって、周波数領域から時間領域に戻ってきます.
ここはよく誤解している人が多いので,よく理解しておきましょう.
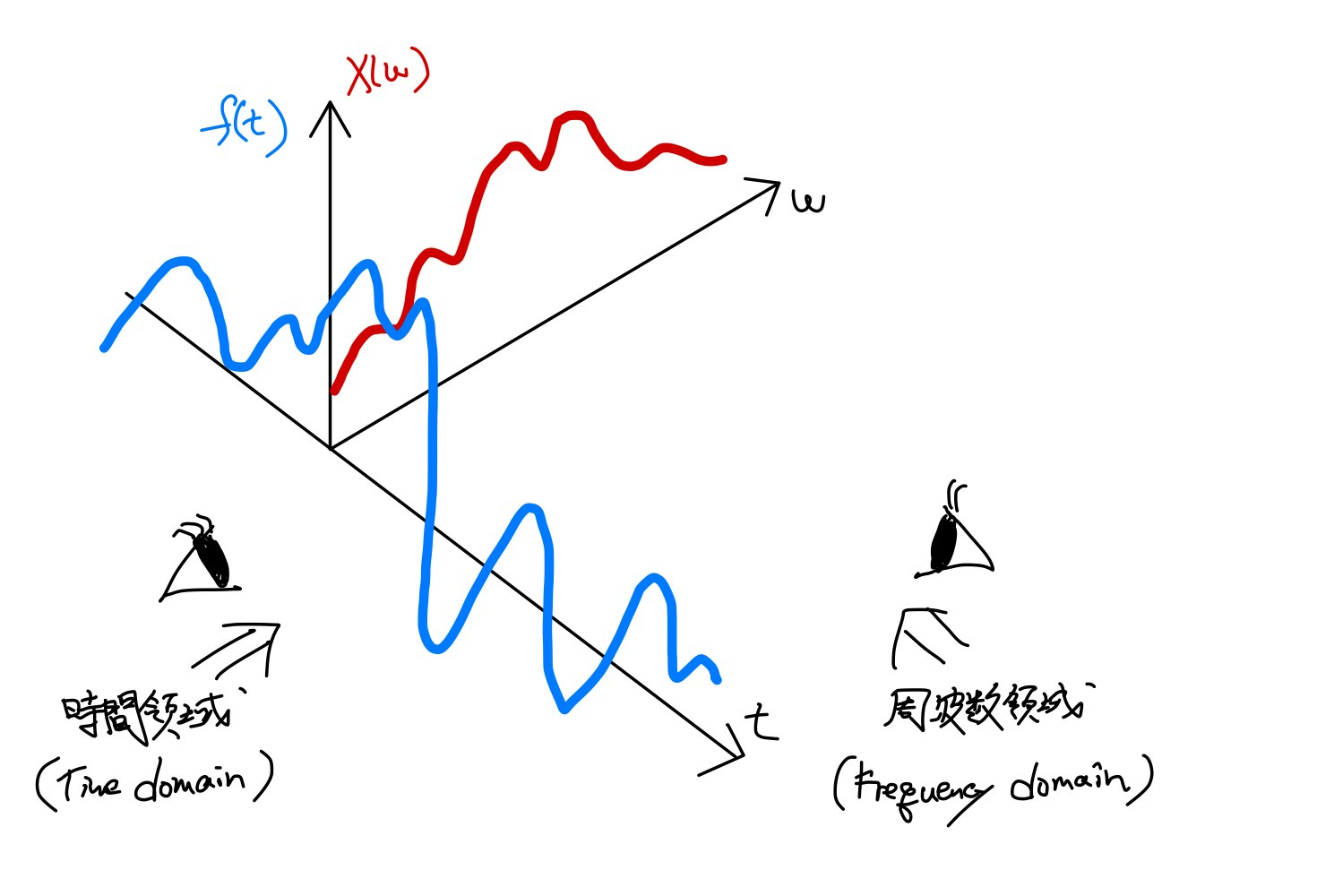 イメージとしては,上のような図を思い浮かべるといいかもしれません.
よく,信号のグラフとその周波数スペクトルを横に並べて見ることが多いと思いますが,その横軸は全く異なっています.上図のように,異なる方向から信号を捉え直しているようなイメージを持つと,混乱を避けれていいかもしれません.
イメージとしては,上のような図を思い浮かべるといいかもしれません.
よく,信号のグラフとその周波数スペクトルを横に並べて見ることが多いと思いますが,その横軸は全く異なっています.上図のように,異なる方向から信号を捉え直しているようなイメージを持つと,混乱を避けれていいかもしれません.
#まとめ
- フーリエ級数展開とは,周期関数を$\cos$波に分解することである.(複素フーリエ級数展開とは,周期関数を螺旋に分解することであるが,本質的には$\cos$波に分解していることに相当する.)
- フーリエ係数は,その周波数成分の振幅と初期位相を,それぞれ絶対値(の2倍)と偏角に表したものである.
- 実関数のフーリエ係数は,正と負のペアが必ず共役であるという縛りがあるため,虚数成分がキャンセリングされて実成分のみが残る.
- フーリエ級数展開は周期的な関数にしか適用できず,周波数スペクトルは離散的になる.
- フーリエ変換は非周期的な関数にも適用でき,周波数スペクトルは連続的になる.
- フーリエ変換は,フーリエ係数を求める過程にあたり,逆フーリエ変換はフーリエ級数展開をする過程にあたる.
複素フーリエ級数展開は初めはとっつきにくいかもしれませんが,図のようなイメージを持てば理解できると思います.
また,上のようなイメージを持っているとフーリエ級数の意味や共役性も,必然的に覚えられると思います.個人的には,隠れた物理的意味を理解していれば,数式だけで理解するよりも遥かに頭に入ってくると思っています.
-
$\cos(k\omega_0 0)=1, \sin(k\omega_0 0)=0$ なので,$f(t) = \sum_{k=0}^{+\infty} \bigl\{ a_k\cos(k\omega_0 t) + b_k\sin(k\omega_0 t)\bigr\}$ のようにサメーションを0からにしてしまっても同じことです.式の上ではこちらの方がすっきりしますが,定常成分という物理的意味をわかりやすくするためにこのように前に出す表記を取っています. ↩
-
下図は$\omega_0$が$\Omega_0$という大文字表記になっています.これは,この図を自分で作ったわけではなく引用してきたからです.連続時間系なので,心の中で$\omega_0$と読み替えていただけると助かります. ↩
-
厳密には $f(t)=t$ は絶対可積分(absolutely integrable)ではないのでフーリエ変換が収束しないのですが,今は気にしません.代わりにラプラス変換を使うことでこの問題は解決できます.詳しくは[この記事]へ. ↩
-
自分でもこれは全く正しい説明とは思えません.ただ,デルタ関数を積分すると1という面積になるという事実から,ある一点に面積値を持った関数だという解釈を持っていても,間違いだとも言えないと思います.その方がイメージしやすいケースもありますし,「ある一点に無限大の値を持っている関数」という解釈と同レベルなものだと思います. ↩