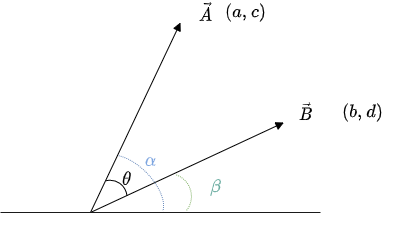-
機械学習を勉強していると内積、外積という言葉がよく出てくる。角度をあらわすんだよ、平行四辺形の面積だよ、画像処理では内積の計算が、相関係数は、みたいにいろんな所ででてくるけどイマイチよくわからなかったのでまとめました。
-
(結論)
内積も外積もただの計算ルール。
例えば二つのベクトルのなす角を知りたい(実際ほとんどこの場合)。その場合は内積という計算ルールで内積を計算すると便利。
平行四辺形の面積だったら外積という計算ルールで外積を計算すると便利。
ただそれだけ。
原点を始点とすると$\cos\theta$は上図より(三角関数の加法定理から)
$$\cos{\theta}=\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \tag{1}$$
ここで、$\vec{A},\vec{B}$の座標から
$$\cos\alpha=\frac{a}{\sqrt{a^2+c^2}} , \cos\beta=\frac{b}{\sqrt{b^2+d^2}},sin\alpha=\frac{c}{\sqrt{a^2+c^2}},\sin\beta=\frac{d}{\sqrt{b^2+d^2}} \tag{2}$$
が求まる。
(1)に代入すると
\begin{align}
\cos\theta&=\frac{a}{\sqrt{a^2+c^2}}\frac{b}{\sqrt{b^2+d^2}}+\frac{c}{\sqrt{a^2+c^2}}\frac{d}{\sqrt{b^2+d^2}}\\
&=\frac{ab+cd}{|\vec{A}||\vec{B}|}\\
&=\frac{\vec{A}\dot{}\vec{B}(内積)}{|\vec{A}||\vec{B}|}
\end{align}
この$\theta$を求めやすくするための演算を内積と定義しているだけ。
2点の座標の演算を以下のように内積と定義している(計算しやすいし定義が分かりやすいから)。
$$\vec{A}\dot{}\vec{B}=ab+cd$$
その演算結果が$|\vec{A}||\vec{B}|\cos\theta$に等しくなるということ。
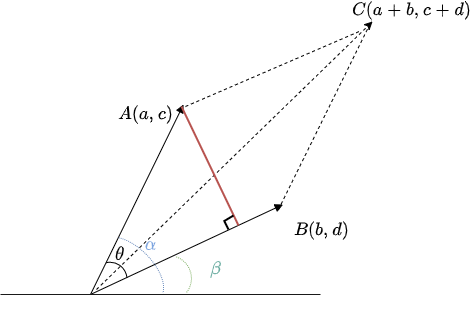
【二つのベクトルでできる平行四辺形の面積が知りたい】
原点を始点として同様に考えていく。まずは
$$\sin{\theta}=\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \tag{1}$$
から、(2)を用いて
\begin{align}
\sin\theta&=\frac{c}{\sqrt{a^2+c^2}}\frac{b}{\sqrt{b^2+d^2}}-\frac{a}{\sqrt{a^2+c^2}}\frac{d}{\sqrt{b^2+d^2}}\\
&=\frac{bc-ad}{|\vec{A}||\vec{B}|}\\
&=\frac{\vec{A}\times\vec{B}(外積)}{|\vec{A}||\vec{B}|}
\end{align}
ここで平行四辺形の面積OACBは$\sin{\theta}$が負になることも考慮して
\begin{align}
平行四辺形OACB&=|\vec{B}|\times|\vec{A}|\times|\sin{\theta}|\\
&=|\vec{A}||\vec{B}|\frac{|\vec{A}\times\vec{B}|}{|\vec{A}||\vec{B}|}\\
&=|\vec{A}\times\vec{B}|(外積)
\end{align}
となる。三角形OABならその面積は2分の1になる。簡単に座標から面積が求められる。
その演算ルールが外積でそのルールが以下となる。
$$|\vec{A}\times\vec{B}|=|ad-bc|$$