前書き
「複雑な環境構築をせずにディープラーニングのチュートリアルができる」をコンセプトとし、この記事のコードをコピペしていくだけで試すことができるようになっています。(と言うかGitHubからクローンしてきて実行するだけ)
環境
macOS Mojave version 10.14.6
python3.6.5
-
この記事の対象読者
タイトル通りGPUなど持っていないけどディープラーニングを試してみたいという方を対象としています。本格的に深層学習をしようとしたらやはりGPUが必要ですが、「何ができるのか」、「どう動くのか」を直感的に理解するには実際に動かしてみるのが良いと思います。
Python自体の環境構築はできていることを前提に進めます。 -
ディープラーニングの定義
情報源によって定義が微妙に異なることがありますが、深層学習やディープラーニングと呼ばれるアルゴリズムはだいたい隠れ層が3層以上からそう呼ばれる事が多い気がしています。(曖昧で申し訳ありません)
この記事では隠れ層の数がそれ以下のモデルも扱いますが特に言い分けたりはしません。ただ、アルゴリズムのことをニューラルネットワーク、それが重み学習することをディープラーニングとします。
R^2スコアは簡単に言うと回帰(予測)した曲線が正解の曲線とどの程度近いかを0〜1で表す評価関数です。MSEは平均二乗和誤差と言って正解の値と予測の値の二乗和誤差の平均値です。
問題設定
2つの入力値(x1, x2)からSinCosカーブを予測する
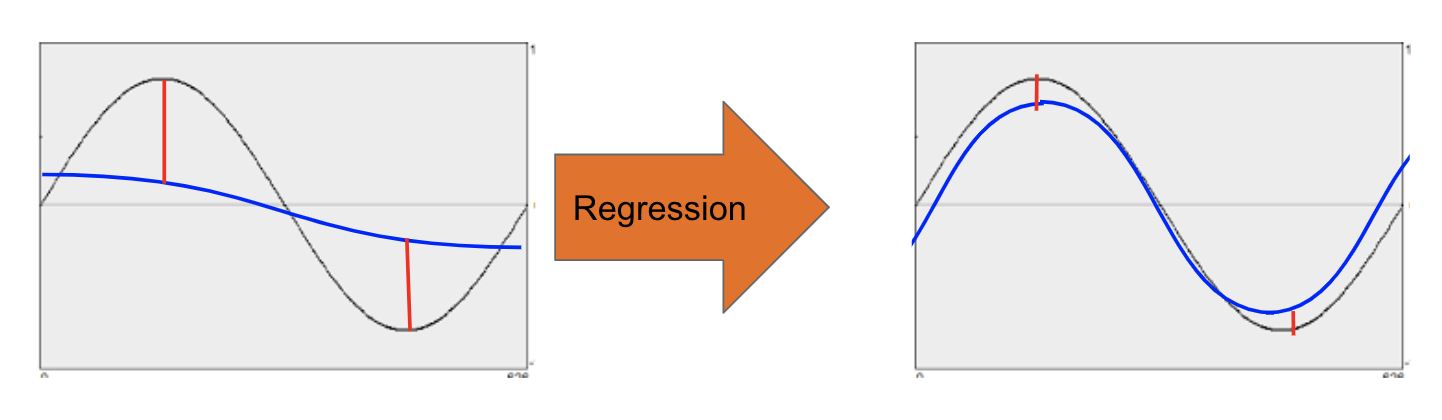
イメージとしてはこのような感じです。
隠れ層の数や各層のユニット数で精度がどう変わるかを確認していきます。
環境構築
# 簡単のため以下の手順で僕が作業したリポジトリをクローンしてきてください。
$ git clone https://github.com/keroido/DNN-learning-Sin-Cos-wave.git
$ cd DNN-learning-Sin-Cos-wave
# 仮想環境を作り、仮想環境に入ります。(任意)
$ pip install virtualenv
$ virtualenv venv
$ . venv/bin/activate
# 仮想環境に必要なライブラリをまとめてインストールします。
(venv)$ pip install -r requirements.txt
# 仮想環境venvから出るときは $ deactivate
学習データを作る
以下の手順でデータセットを作ります。入力値x0,x1とその2つを足した時のSin,Cosの4つの列 × 1000行のデータを生成します。
このx0とx1からSinとCosを予測します。
イメージ
| index | x0 | x1 | Sin | Cos |
|---|---|---|---|---|
| 0 | 50.199163279521 | 17.5983756102216 | 0.925854354002364 | 0.377880556756848 |
| 1 | 127.726947420807 | 116.093208916234 | -0.897413633456196 | -0.441190174966475 |
| 2 | 54.2208002632216 | 116.589734921833 | 0.159699676625697 | -0.987165646325705 |
| 3 | 156.256738791155 | 8.64049515860479 | 0.260551118156132 | -0.965460053460312 |
| : | ... | ... | ... | ... |
| : | ... | ... | ... | ... |
| 999 | 23.2978504439148 | 109.826906405408 | 0.72986697370653 | -0.683589204634239 |
(0 <= x1, x2 <= 180)
以下のディレクトリでデータセットを生成するプログラムを実行します。またトレーニングデータセットの置き場inputと出力結果の置き場outputもここで作っておきます。
# カレントディレクトリを確認する。
$ pwd
[out]: .../DNN-learning-Sin-Cos-wave/code
# 入力データの置き場と出力データの置き場を作る。
$ mkdir ../input ../output
# データセットを生成するプログラムを実行
$ python make_dataset.py
# make_dataset.py
import numpy as np
import pandas as pd
import math
x0 = np.random.rand(1000) * 180
x1 = np.random.rand(1000) * 180
s = [math.sin(math.radians(i+s)) for i, s in zip(x0, x1)]
c = [math.cos(math.radians(i+s)) for i, s in zip(x0, x1)]
df = pd.DataFrame({'x0':x0, 'x1':x1, 'sin':s, 'cos':c})
df.to_csv('../input/data.csv')
するとinputディレクトリにdata.csvが生成されます。
ディープラーニングしてみる
それではいよいよディープラーニングをしてみましょう。この記事のテーマはGPUを使わずにディープラーニングすることですのでscikit-learnで実装します。
また、train.pyとありますが同時に各モデルの評価もしています。
$ pwd
[out]: .../DNN-learning-Sin-Cos-wave/code
$ python train.py
# train.py
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split # データを訓練セットとテストセットに分けます。
from sklearn.neural_network import MLPRegressor # sklearnで動くニューラルんネットワークの関数です。
from sklearn.metrics import mean_squared_error # MSE(平均二乗和誤差)
# inputディレクトリにあるデータを読み込みます。
df = pd.read_csv('../input/data.csv')
df = df.drop('Unnamed: 0', axis=1)
# Xにx0とx1を、yにSinCos
X = df.iloc[:, :2]
y = df.iloc[:, 2:]
# 訓練セットとテストセットに分けます。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 隠れ層の数を2,3,4 ユニットの数を10,50,100,150,200 全ての組み合わせを試す。
hidden_layer_sizes = [(10, 10,), (50, 50,), (100, 100,), (150, 150,), (200, 200,),
(10, 10, 10,), (50, 50, 50,), (100, 100, 100,), (150, 150, 150,), (200, 200, 200,),
(10, 10, 10, 10,), (50, 50, 50, 50,), (100, 100, 100, 100,), (150, 150, 150, 150,), (200, 200, 200, 200,)]
ln = list(range(len(hidden_layer_sizes)))
# Sin,CosそれぞれのMSEとR^2スコアを書き込むデータフレームを作っておく
score_df = pd.DataFrame(columns={'sin_mse', 'cos_mse', 'r^2_score'})
for i, hidden_layer_size in zip(ln, hidden_layer_sizes):
# モデルの詳細(https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html)
# verboseをTrueに変えて実行すると学習の進行状況がわかるようになります。
model = MLPRegressor(activation='relu', alpha=0, batch_size=100,
hidden_layer_sizes=hidden_layer_size, learning_rate_init=0.03,
random_state=0, verbose=False, solver='adam')
# モデルに訓練データセットを食わせます。
model.fit(X_train, y_train)
#テストセットのx0,x1からSin,Cosを予測します。
pred = model.predict(X_test)
# ここから下は予測した結果をoutputディレクトリに出力するデータフレームの整形など
pred = pd.DataFrame(pred)
x = pd.DataFrame({'x':(X_test['x0'] + X_test['x1']).tolist()})
tes = y_test.rename(columns={'sin': 'sin(label)', 'cos': 'cos(label)'}).reset_index(drop=True)
pre = pred.rename(columns={0: 'sin(prediction)', 1: 'cos(prediction)'}).reset_index(drop=True)
ans_df = pd.concat([x, tes, pre], axis=1)
ans_df = ans_df[['x', 'sin(label)', 'sin(prediction)', 'cos(label)', 'cos(prediction)']]
ans_df.to_csv('../output/result_{}_{}_{}.csv'.format(str(i).zfill(2), len(hidden_layer_size), hidden_layer_size[0]))
sin_mse = mean_squared_error(tes['sin(label)'].tolist(), pre['sin(prediction)'].tolist())
cos_mse = mean_squared_error(tes['cos(label)'].tolist(), pre['cos(prediction)'].tolist())
r2 = model.score(X_test, y_test)
score_df.loc['{}'.format(i), 'sin_mse'] = sin_mse
score_df.loc['{}'.format(i), 'cos_mse'] = cos_mse
score_df.loc['{}'.format(i), 'r^2_score'] = r2
col = ['sin_mse', 'cos_mse', 'r^2_score']
score_df = score_df[col]
# outputディレクトリに出力する
score_df.to_csv('../output/score.csv')
解説
(コードが汚くて申し訳ないのですが、、、)hidden_layer_sizesを見てください。ここでは以下のようにニューラルネットワークのレイヤー数(隠れ層数)とユニット数を色々変えてどの組み合わせが良い精度を出せるかを試行錯誤できるようにしています。
| レイヤー数 \ ユニット数 | 10 | 50 | 100 | 150 | 200 |
|---|---|---|---|---|---|
| 2 | 精 | 度 | が | 良 | く |
| 3 | な | る | 組 | み | 合 |
| 4 | わ | せ | は | 何 | ? |
評価、可視化してみる
可視化にはjupyter notebookが便利なので利用していきましょう。
$ pip install jupyter
$ pwd
[out]: .../DNN-learning-Sin-Cos-wave/code
$ ls
[out]: make_dataset.py train.py viewer.ipynb
$ jupyter notebook
ブラウザでjupyter notebookが起動したらviewer.ipynbを開いてください。このノートブックは上から実行していくだけで評価とデータの可視化ができるようになっています。
https://github.com/keroido/DNN-learning-Sin-Cos-wave/blob/master/code/viewer.ipynb
以下jupyter上での実行です。(説明不要のコードは省略)
outputディレクトリを見てみると'result_00_2_10.csv'などと名前のついたcsvファイルが15個存在しています。このファイルの名前は'result_00_2_10.csv'を例にとって説明すると、00は作成した順番で2はレイヤー数、10はユニット数を表しています。ですからこのcsvファイルは「0番目に作った2層10ユニットづつのニューラルネットワークで学習した結果ですよ」と言う事になります。
!ls ../output
[out]:
result_00_2_10.csv result_04_2_200.csv result_08_3_150.csv result_12_4_100.csv
result_01_2_50.csv result_05_3_10.csv result_09_3_200.csv result_13_4_150.csv
result_02_2_100.csv result_06_3_50.csv result_10_4_10.csv result_14_4_200.csv
result_03_2_150.csv result_07_3_100.csv result_11_4_50.csv score.csv
1, 各ニューラルネットワークのスコアを確認
score_df = pd.read_csv('../output/score.csv')
score_df = score_df.drop('Unnamed: 0', axis=1)
score_df
どんな条件の時にR^2スコアの値が良いかを確認してみましょう。 結果を見てみると9番目、result_09_3_200.csvの3層200ユニットのニューラルネットワークが最も良い結果を出しています。(設定によって変わるかもしれません)
単純に層が深ければ良いと言うわけではないことがわかりますね。
| index | sin_mse | cos_mse | r^2_score |
|---|---|---|---|
| 0 | 0.118307 | 0.272191 | 0.551913 |
| 1 | 0.071344 | 0.174416 | 0.717997 |
| 2 | 0.101467 | 0.269444 | 0.574389 |
| 3 | 0.053282 | 0.022353 | 0.913211 |
| 4 | 0.374317 | 0.242327 | 0.292416 |
| 5 | 0.127534 | 0.274327 | 0.538875 |
| 6 | 0.061558 | 0.163282 | 0.742001 |
| 7 | 0.195692 | 0.262261 | 0.474512 |
| 8 | 0.034099 | 0.010542 | 0.948776 |
| 9 | 0.006197 | 0.004922 | 0.987241 |
| 10 | 0.512035 | 0.361053 | -0.001846 |
| 11 | 0.116843 | 0.099484 | 0.751770 |
| 12 | 0.013951 | 0.029560 | 0.950072 |
| 13 | 0.009213 | 0.009595 | 0.978419 |
| 14 | 0.005862 | 0.006255 | 0.986096 |
2, 一番良いスコアを出したcsvファイルを確認
tmp = pd.read_csv('../output/result_09_3_200.csv')
tmp = tmp.drop('Unnamed: 0', axis=1)
tmp
(label)が正解ラベルで、(prediction)がニューラルネットワークの予測値です。割と近い値を予測できているのがわかります。
※ここでのxはx0,x1の和です。
| x | sin(label) | sin(prediction) | cos(label) | cos(prediction) |
|---|---|---|---|---|
| 0 | 271.800382 | -0.999506 | -0.912688 | 0.031417 |
| 1 | 133.334658 | 0.727358 | 0.722477 | -0.686258 |
| 2 | 136.451163 | 0.688973 | 0.656727 | -0.724787 |
| 3 | 187.429195 | -0.129301 | -0.182335 | -0.991605 |
| 4 | 229.748855 | -0.763220 | -0.801409 | -0.646139 |
| ... | ... | ... | ... | ... |
3, 実際に可視化してみる
files = glob.glob('../output/result*.csv')
files.sort()
csvs = []
t = []
for i in range(1, 16):
t.append(files[i-1])
if i%5 == 0:
csvs.append(t)
t = []
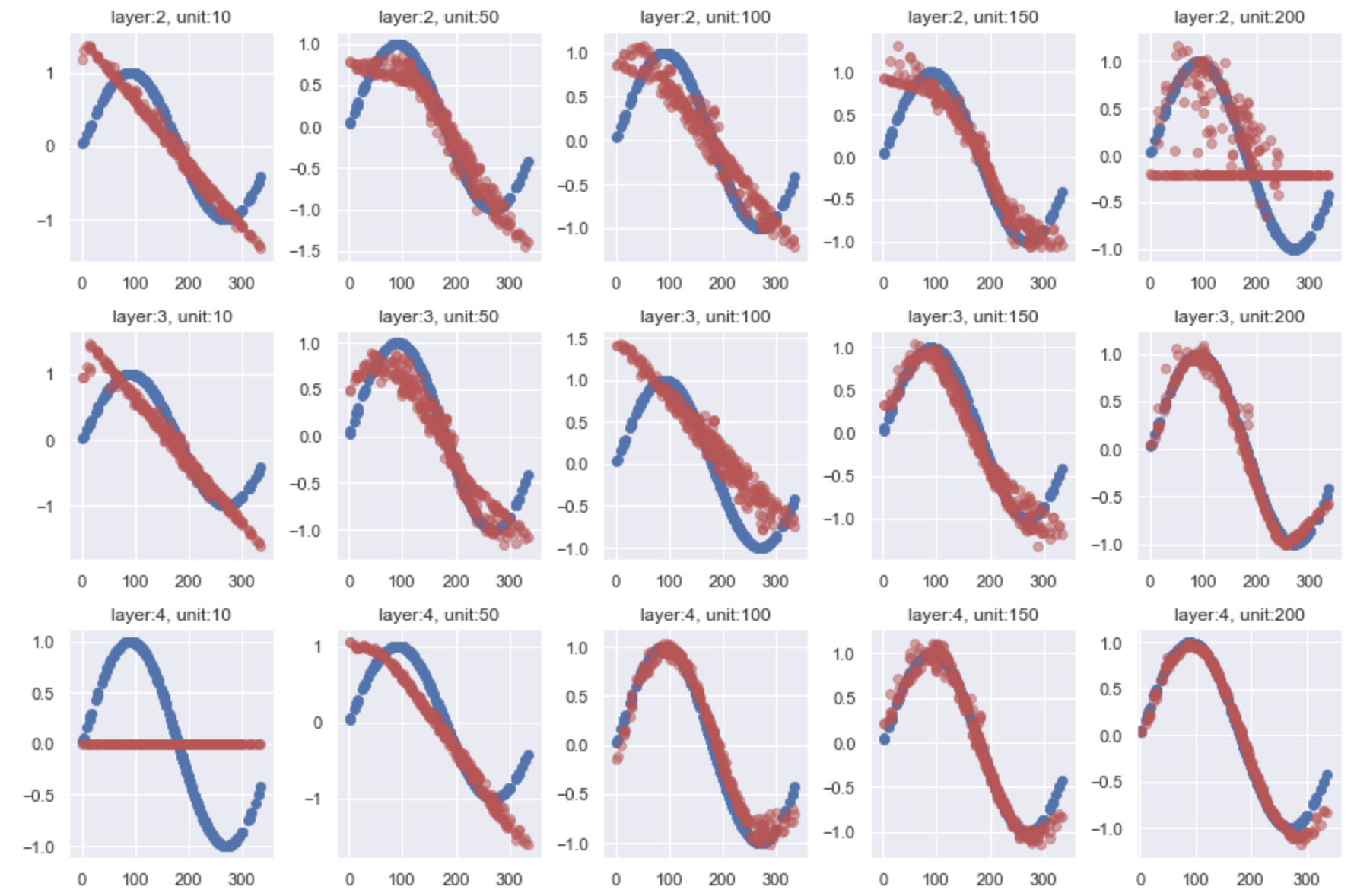
Sin
fig, axes = plt.subplots(3, 5, figsize=(15, 10))
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i in range(3):
for j in range(5):
tmp = pd.read_csv(csvs[i][j])
axes[i, j].scatter(tmp.loc[:, 'x'], tmp.loc[:, 'sin(label)'], c='b')
axes[i, j].scatter(tmp.loc[:, 'x'], tmp.loc[:, 'sin(prediction)'], c='r', alpha=0.5)
axes[i, j].set_title('layer:{}, unit:{}'.format(csvs[i][j][20], csvs[i][j][22:-4]))
plt.xlim(-5, 365)
cos
fig, axes = plt.subplots(3, 5, figsize=(15, 10))
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i in range(3):
for j in range(5):
tmp = pd.read_csv(csvs[i][j])
axes[i, j].scatter(tmp.loc[:, 'x'], tmp.loc[:, 'cos(label)'], c='b')
axes[i, j].scatter(tmp.loc[:, 'x'], tmp.loc[:, 'cos(prediction)'], c='r', alpha=0.5)
axes[i, j].set_title('layer:{}, unit:{}'.format(csvs[i][j][20], csvs[i][j][22:-4]))
plt.xlim(-5, 365)
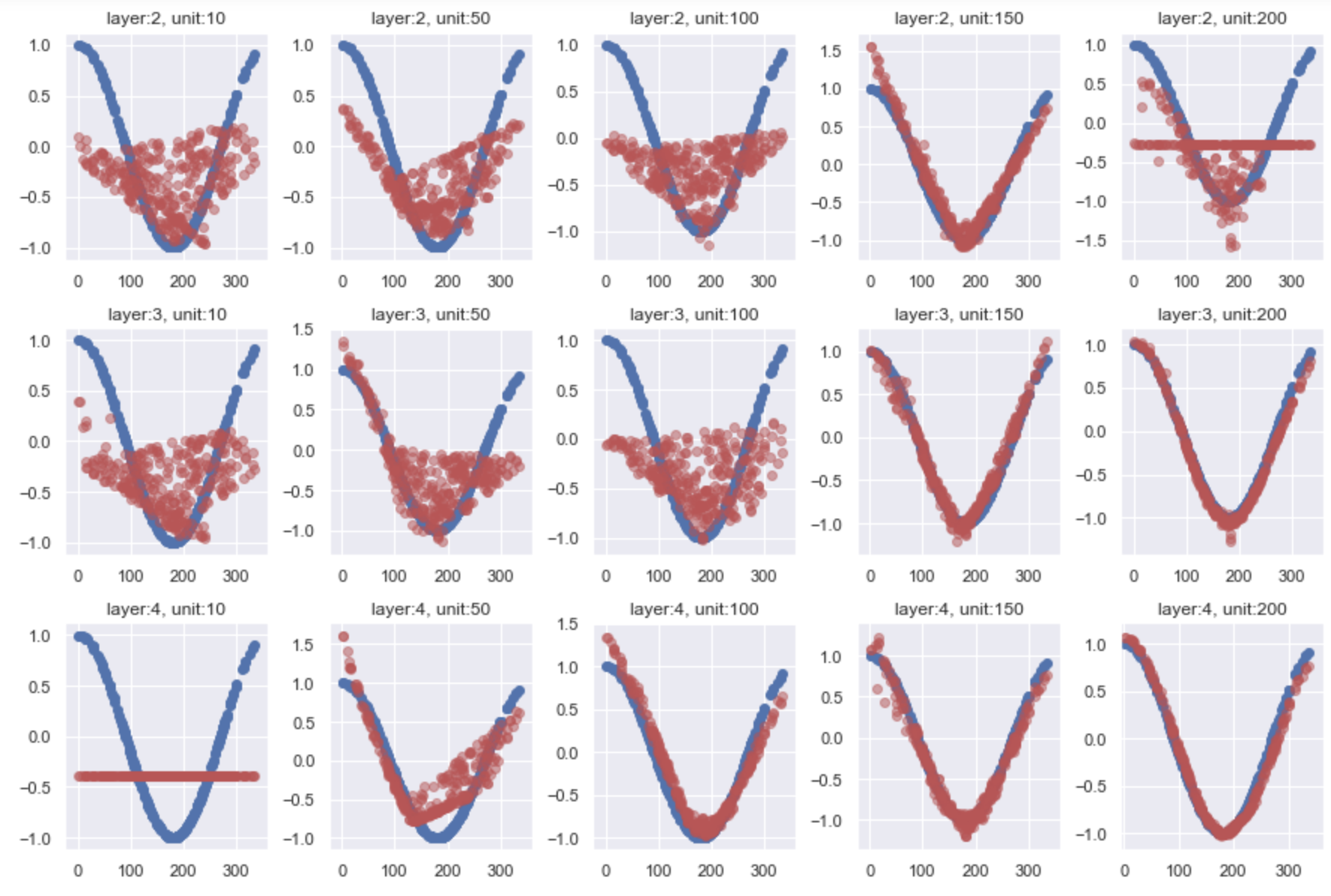
可視化してみるとニューラルネットワークがどう予測したかが一目でわかって楽しいですね。
以上で「GPU持ってないけどDeep Learningしてみる」終わりです。お疲れ様でした。