概要
ゲームAIに関して勉強し始めたので,その備忘録.
本記事では,人間的な曖昧性をコンピュータに適用するファジー理論について記述する.
参考
以下の書籍を用いた.
ゲーム開発者のためのAI入門
また,以下のサイト辺りが良さそうな気配がした.
ファジィ理論の数学的基礎
事前準備
ベクトル計算用の構造体,便利関数の準備と,
角度計算用のマクロの準備を行う.
//角度計算用マクロ.
# define L_PI (3.1415f)
# define L_2PI (6.2830f)
# define L_H_DEG (180.0000f)
# define L_DEG (360.0000f)
# define DEG2RAD(e) ((e)*(L_PI)/(L_H_DEG))
# define RAD2DEG(e) ((e)*(L_H_DEG)/(L_PI))
# define ADJUST_RAD(e) (((e)<(0.0000f))?(e)+(L_2PI):((e)>(L_2PI))?(e)-(L_2PI):(e))
# define ADJUST_DEG(e) (((e)<(0.0000f))?(e)+(L_DEG):((e)>(L_DEG))?(e)-(L_DEG):(e))
# define CLIP(e,l,h) (min(max(e,l),h))
//ベクトル構造体.
# define VECTOR SVector2D<float>
template <class T>
struct SVector2D
{
typedef T DataType;
T x;
T y;
SVector2D(){ Init(); }
void Init()
{
x = T();
y = T();
}
SVector2D operator + ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x + e.x; tmp.y = y + e.y; return tmp; }
SVector2D& operator += ( const SVector2D& e ){ x += e.x; y += e.y; return (*this); }
SVector2D operator - ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x - e.x; tmp.y = y - e.y; return tmp; }
SVector2D& operator -= ( const SVector2D& e ){ x -= e.x; y -= e.y; return (*this); }
T operator * ( const SVector2D& e ) const { return ( x * e.x ) + ( y * e.y ); }
SVector2D& operator *= ( const int e ){ x *= e; y *= e; return (*this); }
SVector2D& operator *= ( const float e ){ x *= e; y *= e; return (*this); }
SVector2D& operator /= ( const int e ){ x /= e; y /= e; return (*this); }
SVector2D& operator /= ( const float e ){ x /= e; y /= e; return (*this); }
};
//数学関連の関数群.
namespace LMath
{
VECTOR::DataType GetScalar( VECTOR vec )
{
return sqrtf( vec.x * vec.x + vec.y * vec.y );
}
VECTOR Normalize( VECTOR vec )
{
const VECTOR::DataType vecLen = GetScalar( vec );
vec.x /= vecLen;
vec.y /= vecLen;
return vec;
}
VECTOR Normalize( VECTOR from, VECTOR to )
{
VECTOR tmp = to - from;
return Normalize( tmp );
}
float GetRotateRad( const float from, const float to )
{
//角度候補1.
const float dir1st = ( to - from );
const float dir1stVal = fabsf( dir1st );
//角度候補2.
const float dir2ndVal = ( L_2PI - dir1stVal );
const float dir2nd = ((dir1st>=0.0f)?-1.0f:1.0f) * dir2ndVal;
//絶対値が小さい方を採用.
return ( dir1stVal > dir2ndVal ) ? dir2nd : dir1st;
}
bool IsCollisionCircle( const VECTOR& pos1, const VECTOR& pos2, const float r )
{
VECTOR tmp = pos1 - pos2;
return ( GetScalar( tmp ) < r );
}
};
ファジー理論
概要
通常,コンピュータで物事を判断する際には,とある集合に「属するか」「属さないか」で判断する.
例えば,物体AとBの間の距離に関して考えると,適当な閾値を設定し,閾値以下なら「近い」集合に属し,
閾値を超えるなら「近い」集合に属さない,つまり「遠い」という判定になる.
このような二値で判断する集合をクリスプ集合と呼ぶが,人間的な曖昧性を考慮すると,
必ずしも全ての事柄を二値で判断できるわけではないことは分かると思う.
上記例をもう一度取り上げると,閾値+0.001fという距離であっても「遠い」という判定になってしまうわけだが,
主観的には閾値とほぼ変わらないわけなので,「遠い」というよりは
「少し近い」とか「それなりに近い」とかそういう判定が望ましいわけである.
そこで,0か1か,ではなく,0~1の間の変動も考慮しよう,と考えられた集合がファジー集合であり,
そのファジー集合を用いてコンピュータでも曖昧な状態を扱えるようにしよう,と考えられたのが,
ファジー理論・制御である.
ちなみに,ファジー集合は0~1の範囲をとることから,クリスプ集合はファジー集合の特殊ケースと考えることができる.
具体的な処理の制御は以下の通りである.
1,ファジー化
クリスプ集合を入力時ファジー集合に変換する.
2,ファジー推論
入力時ファジー集合を組み合わせて出力時ファジー集合を生成する.
3,非ファジー化
出力時ファジー集合をクリスプ集合に変換する.
ファジー化
入力として受け取ったクリスプ集合を,入力時ファジー集合に変換する.
変換にはメンバーシップ関数とヘッジ関数が用いられる.
メンバーシップ関数
クリスプ集合を入力として受取り,クリスプ集合の各要素に関して,
ファジー集合への帰属度を表す0~1の実数を返す.
メンバーシップ関数は以下のように,各ファジー集合に合わせて一つずつ定義する.
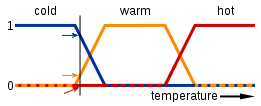
(引用:ファジィ論理)
図からわかるように,メンバーシップ関数の形状は,斜辺や三角形,台形など様々なものがある.
これはファジー理論を適用するシステムの要件などに応じて,適切なものを用意する必要がある.
以下に,一般的なメンバーシップ関数(斜辺,三角形,台形)の実装例を示す.
//斜辺.
float FuzzyGrade( float value, float x0, float x1 )
{
assert( x0 <= x1 );
if( value < x0 ){ return 0.0f; }
if( value >= x1 ){ return 1.0f; }
if( x0 <= value && value < x1 ){
return ( value - x0 ) / ( x1 - x0 );
}
return -1.0f;
}
//三角形.
float FuzzyTriangle( float value, float x0, float x1, float x2 )
{
assert( x0 <= x1 );
assert( x1 <= x2 );
if( value < x0 ){ return 0.0f; }
if( value >= x2 ){ return 0.0f; }
if( x0 <= value && value < x1 ){
return FuzzyGrade( value, x0, x1 );
}
if( x1 <= value && value < x2 ){
return FuzzyNot( FuzzyGrade( value, x1, x2 ) );
}
return -1.0f;
}
//台形.
float FuzzyTrapenoid( float value, float x0, float x1, float x2, float x3 )
{
assert( x0 <= x1 );
assert( x1 <= x2 );
assert( x2 <= x3 );
if( value < x0 ){ return 0.0f; }
if( value >= x3 ){ return 0.0f; }
if( x1 <= value && value < x2 ){ return 1.0f; }
if( x0 <= value && value < x1 ){
return FuzzyGrade( value, x0, x1 );
}
if( x2 <= value && value < x3 ){
return FuzzyNot( FuzzyGrade( value, x2, x3 ) );
}
return -1.0f;
}
FuzzyNot関数はファジー論理の否定を表す関数である.
処理内容などは後述するが,ここでは論理演算同様,結果が反転することが分かれば良い.
ヘッジ関数
メンバーシップ関数の結果を特定の方向に補正する関数.
言語的には「非常に」といった副詞的な役割である.
これを通すと,本来のメンバーシップ関数は歪んでしまうので,使用には注意が必要である.
以下に,一般的なヘッジ関数(VERY,NOT_VERY)の実装例を示す.
//powf関数は指数関数である.大抵は標準関数ライブラリに用意されている.
float HedgeVery( float a ){ return powf( a, 2.0f ); }
float HedgeNotVery( float a ){ return powf( a, 0.5f ); }
例
以下にファジー化の実装例を示す.
//ファジー集合群.近い,普通,遠いの三状態.
float distNear = 0.0f;
float distNormal = 0.0f;
float distFar = 0.0f;
{
VECTOR posA = /*敵の位置*/;
VECTOR posB = /*プレイヤーの位置*/;
//クリスプ集合の1要素.「近い」集合の1要素をファジー集合に当てはめる.
float dist = LMath::GetScalar( posA - posB );
distNear = FuzzyNot( FuzzyGrade( dist, 75.0f, 125.0f ) );
distNormal = FuzzyTrapenoid( dist, 75.0f, 125.0f, 200.0f, 250.0f );
distFar = FuzzyGrade( dist, 225.0f, 250.0f );
}
ファジー推論
ファジー化によって得られた入力時ファジー集合に対して,
ファジールールに基いた論理演算を行い,出力時ファジー集合を生成する.
ここでの論理演算とは,0と1の組み合わせで表現される通常の論理演算ではなく,
ファジー集合専用で用いられるファジー論理を指す.
ファジールール
ファジールールとは,ファジー集合をファジー論理を用いて論理演算する際のルール,である.
定形はなく,どういったファジー集合を出力したいかによって決めることになる.
以下は,距離に関するファジー集合を用いて,敵の状態に関するファジー集合を生成する処理を日本語で示したものである.
IF 近い OR 普通 THEN 敵の状態 = 追跡
IF 遠い THEN 敵の状態 = 哨戒
ファジー論理
ファジー集合は0~1の値を取るため,0と1を組み合わせて表現する通常の論理演算は使用できない.そこでファジー集合用に用意された論理演算がファジー論理である.
一般的にはOR,AND,NOTが定義される.
以下に一般的な実装例を示す.
float FuzzyAnd( float a, float b ){ return fminf( a, b ); }
float FuzzyOr( float a, float b ){ return fmaxf( a, b ); }
float FuzzyNot( float a ){ return 1.0f - a; }
他にも,確率の和集合や積集合として定義することもある.
上記関数で上手く行かない場合は,試してみると良いかもしれない.
例
以下にファジー推論の実装例を示す.
//ファジー集合群.敵の状態として,追跡と哨戒を考える.
float stateChase = 0.0f;
float statePatrol = 0.0f;
{
//入力時ファジー集合が「近い」だった場合は「追跡」ファジー集合に.
stateChase = distNear;
//入力時ファジー集合が「普通」,「遠い」だった場合は,「哨戒」ファジー集合に.
statePatrol = FuzzyOr( distNormal, distFar );
}
非ファジー化
ファジー推論によって得られたファジー集合を基に,クリスプ集合を生成する.
こちらもファジールール同様,定形は存在しないため,その時々に合わせて適切な変換を行う必要がある.
なお一般的には,最終的に決定されたクリスプ集合の他に,クリスプ集合選択に大きく寄与したファジー集合の値も取得できるようにする.
例
enum STATE_TYPE
{
STATE_TYPE_CHASE = 0,
STATE_TYPE_PATROL,
STATE_TYPE_NUM,
STATE_TYPE_INVALID = -1,
};
STATE_TYPE g_nextState;
.
.
.
//非ファジー化.
float fuzzyValue = 0.0f;
{
if( stateChase >= statePatrol ){
fuzzyValue = stateChase;
g_nextState = STATE_TYPE_CHASE;
}
else{
fuzzyValue = statePatrol;
g_nextState = STATE_TYPE_PATROL;
}
}
fuzzyValueを活用することで,「速度の遅い追跡」「周辺警戒に近い追跡」といった,
追跡状態の中での状態変化も表現することができる.
例
今まで例示で上げてきた処理を組み合わせると以下のようになる.
自分と敵の相対距離から,「近い」「普通」「遠い」という距離に関するファジー集合を生成し,
その三状態から「追跡」「哨戒」という敵の状態に関するファジー集合を生成している.
最後に,クリスプ集合に戻せば終了である.
enum STATE_TYPE
{
STATE_TYPE_CHASE = 0,
STATE_TYPE_PATROL,
STATE_TYPE_NUM,
STATE_TYPE_INVALID = -1,
};
STATE_TYPE g_nextState;
float Exec()
{
//ファジー化.
float distNear = 0.0f;
float distNormal = 0.0f;
float distFar = 0.0f;
{
VECTOR posA = /*敵の位置*/;
VECTOR posB = /*プレイヤーの位置*/;
//クリスプ集合の1要素.「近い」集合の1要素をファジー集合に当てはめる.
float dist = LMath::GetScalar( posA - posB );
distNear = FuzzyNot( FuzzyGrade( dist, 75.0f, 125.0f ) );
distNormal = FuzzyTrapenoid( dist, 75.0f, 125.0f, 200.0f, 250.0f );
distFar = FuzzyGrade( dist, 225.0f, 250.0f );
}
//ファジールール.
float stateChase = 0.0f;
float statePatrol = 0.0f;
{
stateChase = distNear;
statePatrol = FuzzyOr( distNormal, distFar );
}
//非ファジー化.
float fuzzyValue = 0.0f;
{
if( stateChase >= statePatrol ){
fuzzyValue = stateChase;
g_nextState = STATE_TYPE_CHASE;
}
else{
fuzzyValue = statePatrol;
g_nextState = STATE_TYPE_PATROL;
}
}
return fuzzyValue;
}
動作状況
実際にビジュアライザで動かした結果.
追跡状態になった時にいくつかの矩形が見えるが,これは追跡時の経路探索アルゴリズムに
【ゲームAI】A*アルゴリズム+影響マップを使った結果,ウェイポイントが描画されているだけである.
消してもよかったが,状態が変わったことがすぐに分かるのでそのままにした.
総括
ゲームAIの「思考」部分として,比較的容易に実装できるのはとても良い.
調整箇所は,メンバーシップ関数,ヘッジ関数,ファジールール,非ファジー化と多めではあるが,
そこまで複雑に絡み合っているものでもないので,あまりコストもかからないだろう.
ただし,新しい入力用ファジー集合,出力用ファジー集合の組み合わせを実現するためには,
その度に関数実装が必要になるため,上手くデータドリヴン化する必要はあると思われる.
