【ゲームAI】フロッキングアルゴリズム

概要

ゲームAIに関して勉強し始めたので，その備忘録．
この記事ではフロッキングアルゴリズムについて記述する．
フロッキングアルゴリズムとは，群れ行動をシミュレートするアルゴリズムである．
実装方法は多種多様であると思うが，ここではBoidsを取り上げる．

なお，この記事では連続的なゲームを想定したサンプルを示す．
離散的なゲームでのフロッキングアルゴリズムも，考え方は同じである．

参考書

ありきたりではあるが以下の書籍を用いた．
ゲーム開発者のためのAI入門

Boids

概要

このアルゴリズムは1987年に発表された
Flocks, Herds, and Schools:A Distributed Behavioral Modelで提唱されたもので，
Boidsとは「シミュレートされた集団」を指し，Boidが各個体を指している．

このアルゴリズムは，以下の三つのルールで構成されている．
●結合：自分の視野範囲にいるBoidの平均位置に向かう．
●整列：自分の視野範囲にいるBoidの平均方向に向かう．
●分離：自分の視野範囲にいるBoidに近づきすぎている場合は，離れる方向に向かう．

各ルールを適用した時に算出される移動方向は累積され，
全ルール適用後の累積方向が，最終的な移動方向となる．

今回は上記ルールに加えて，以下のルールも適用している．
●障害物回避：自分の視線方向に障害物がある場合は避ける.

事前準備

ベクトル計算用の構造体，便利関数の準備と，
角度計算用のマクロの準備を行う．

//角度計算用マクロ.
#define L_PI        (3.1415f)
#define L_2PI       (6.2830f)
#define L_H_DEG     (180.0000f)
#define L_DEG       (360.0000f)
#define DEG2RAD(e) ((e)*(L_PI)/(L_H_DEG))
#define RAD2DEG(e) ((e)*(L_H_DEG)/(L_PI))
#define ADJUST_RAD(e) (((e)<(0.0000f))?(e)+(L_2PI):((e)>(L_2PI))?(e)-(L_2PI):(e))
#define ADJUST_DEG(e) (((e)<(0.0000f))?(e)+(L_DEG):((e)>(L_DEG))?(e)-(L_DEG):(e))

//ベクトル構造体.
#define VECTOR SVector2D<float>
template <class T>
struct SVector2D
{
    typedef T DataType;
    T x;
    T y;
    SVector2D(){ Init(); }
    void Init()
    {
        x = T();
        y = T();
    }
    SVector2D   operator +  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x + e.x; tmp.y = y + e.y; return tmp; }
    SVector2D&  operator += ( const SVector2D& e ){ x += e.x; y += e.y; return (*this); }
    SVector2D   operator -  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x - e.x; tmp.y = y - e.y; return tmp; }
    SVector2D&  operator -= ( const SVector2D& e ){ x -= e.x; y -= e.y; return (*this); }
    T           operator *  ( const SVector2D& e ) const { return ( x * e.x ) + ( y * e.y ); }
    SVector2D&  operator *= ( const int e ){ x *= e; y *= e; return (*this); }
    SVector2D&  operator *= ( const float e ){ x *= e; y *= e; return (*this); }
    SVector2D&  operator /= ( const int e ){ x /= e; y /= e; return (*this); }
    SVector2D&  operator /= ( const float e ){ x /= e; y /= e; return (*this); }
};

//数学関連の関数群.
namespace LMath
{
    VECTOR::DataType GetScalar( VECTOR vec )
    {
        return sqrtf( vec.x * vec.x + vec.y * vec.y );
    }

    VECTOR Normalize( VECTOR vec )
    {
        const VECTOR::DataType vecLen = GetScalar( vec );
        vec.x /= vecLen;
        vec.y /= vecLen;
        return vec;
    }

    VECTOR Normalize( VECTOR from, VECTOR to )
    {
        VECTOR tmp = to - from;
        return Normalize( tmp );
    }

    float GetRotateRad( const float from, const float to )
    {
        //角度候補1.
        const float dir1st      = ( to - from );
        const float dir1stVal   = fabsf( dir1st );

        //角度候補2.
        const float dir2ndVal   = ( L_2PI - dir1stVal );
        const float dir2nd      = ((dir1st>=0.0f)?-1.0f:1.0f) * dir2ndVal;

        //絶対値が小さい方を採用.
        return ( dir1stVal > dir2ndVal ) ? dir2nd : dir1st;
    }

    bool IsCollisionCircle( const VECTOR& pos1, const VECTOR& pos2, const float r )
    {
        VECTOR tmp = pos1 - pos2;
        return ( GetScalar( tmp ) < r );
    }
};

サンプル

//視野のrとθ
#define VIEW_RANGE_MAX      (75.0f)
#define VIEW_RADIUS_MAX     (DEG2RAD(180.0f))

//分離判定用閾値と最大分離角度.
#define SEPARATE_RANGE_MAX  (30.0f)
#define SEPARATE_DIR_MAX    (DEG2RAD(60.0f))

//障害物検知距離と障害物検知範囲，最大回避角度.
#define CHECK_OBSTACLE_DISTANCE ( 80.0f )
#define CHECK_OBSTACLE_RANGE    ( 60.0f )
#define CHECK_OBSTACLE_RADIUS   (DEG2RAD(60.0f))

//各種パラメータ.
VECTOR g_avePos;
float g_avePosNum;
float g_aveDir;
float g_aveDirNum;
float g_separateDir;
float g_obsAvoidDir;

void InitParam()
{
    g_avePos.Init(); m_avePos.x = m_avePos.y = 0.0f;
    g_avePosNum = 0;
    g_aveDir    = 0.0f;
    g_aveDirNum = 0;
    g_separateDir = 0.0f;
    g_obsAvoidDir = 0.0f;
}

void Update( VECTOR& selfPos, float& selfDir, const float selfVel )
{
    //初期化.
    InitParam();

    //現在方向の単位ベクトル.
    VECTOR selfDirVec;
    selfDirVec.x = cosf( selfDir );
    selfDirVec.y = -sinf( selfDir );

    //死角(ローカル座標での).
    const float deadAngleStart  = ADJUST_RAD( VIEW_RADIUS_MAX / 2.0f );
    const float deadAngleEnd    = ADJUST_RAD( -(VIEW_RADIUS_MAX / 2.0f) );

    int inViewNum = 0;
    VECTOR* posArray = /*周辺の動的モジュールの位置リスト*/;
    float* dirArray = /*周辺の動的モジュールの方向リスト*/;
    int arrayNum = /*動的モジュールリストのサイズ*/;
    for( int i = 0; i < arrayNum; ++i ){
        if( /*自分だったら*/ ){ continue; }

        //距離チェック.
        VECTOR  relativePos = posArray[i] - selfPos;
        const float relativeLen = LMath::GetScalar( relativePos );
        if( relativeLen > VIEW_RANGE_MAX ){
            continue;
        }

        //オブジェクトへの角度をベクトルから逆算.
        float targetDir = ADJUST_RAD( atan2f( -relativePos.y, relativePos.x ) );

        //自分を0度とした時の角度に変換
        targetDir = ADJUST_RAD( targetDir - selfDir );

        //死角なら考慮しない.
        if( deadAngleStart <= targetDir && targetDir <= deadAngleEnd ){
            continue;
        }

        //視界に入っているオブジェクトが増えた.
        inViewNum++;

        //結合の累積.
        {
            g_avePos += relativePos;
            g_avePosNum++;
        }

        //整列の累積.
        {
            g_aveDir += LMath::GetRotateRad( selfDir, dirArray[i] );
            g_aveDirNum++;
        }

        //分離の累積.
        if( relativeLen <= SEPARATE_RANGE_MAX )
        {
            //オブジェクトがいる方向とは逆側に回転したい.
            const float multi   = ( targetDir <= L_PI ) ? -1.0f : 1.0f;
            const float coef    = ( SEPARATE_RANGE_MAX - relativeLen ) / SEPARATE_RANGE_MAX;
            g_separateDir += multi * ( SEPARATE_DIR_MAX * coef );
        }
    }

    //障害物検知.
    VECTOR* obsPosArray = /*周辺の障害物の位置リスト*/;
    int obsArrayNum = /*障害物リストのサイズ*/;
    for( int i = 0; i < obsArrayNum; ++i ){
        //障害物との距離.
        VECTOR disObs = obsPosArray[i] - selfPos;

        //視線上への正射影.
        //(方向ベクトルが単位ベクトルじゃないと正しい長さは出ない).
        VECTOR checkProject = selfDirVec;
        checkProject *= ( disObs * selfDirVec );

        //視線距離よりも正射影の方が長い場合は，そもそもチェック範囲に入っていないので無視.
        const float projectScalar = LMath::GetScalar( checkProject );
        if( CHECK_OBSTACLE_DISTANCE < projectScalar ){ continue; }

        //障害物周辺を向いていない場合も無視.
        if( !LMath::IsCollisionCircle( checkProject, disObs, CHECK_OBSTACLE_RANGE ) ){
            continue;
        }

        //向き.
        float disObsDir = ADJUST_RAD( atan2f( -disObs.y, disObs.x ) );
        disObsDir = ADJUST_RAD( disObsDir - selfDir );

        //障害物にぶつからない方向に曲がる.
        const float m       = ( disObsDir <= L_PI ) ? -1.0f : 1.0f;
        const float coef    = ( CHECK_OBSTACLE_DISTANCE - projectScalar ) / CHECK_OBSTACLE_DISTANCE;
        g_obsAvoidDir += m * CHECK_OBSTACLE_RADIUS * coef;
    }

    if( inViewNum > 0 ){
        //何かが自分の視野内に入っている.

        //自分の分も平均に含める.
        g_avePosNum++;
        g_aveDirNum++;

        //各ルールの適用.
        {
            float dir = 0.0f;

            //結合.
            if( 0 < g_avePosNum )
            {
                g_avePos /= (float)g_avePosNum;
                const float absoluteDir = ADJUST_RAD( atan2f( -g_avePos.y, g_avePos.x ) );
                dir += LMath::GetRotateRad( selfDir, absoluteDir );
            }

            //整列.
            if( 0 < g_aveDirNum )
            {
                g_aveDir /= ( float )g_aveDirNum;
                dir += g_aveDir;
            }

            //分離.
            {
                dir += g_separateDir;
            }

            //障害物回避.
            {
                dir += g_obsAvoidDir;
            }

            //0～L_2PIの範囲に入るように調整.
            while( (dir < 0.000f) || (dir > L_2PI) ){
                dir = ADJUST_RAD( dir );
            }

            //方向を更新.
            selfDir = ADJUST_RAD( selfDir + dir );

            //位置を更新.
            selfPos.x += selfVel * cosf( selfDir );
            selfPos.y += selfVel * -sinf( selfDir );
        }
    }
    else{
        //視野内に何もいないので，自分で行先を決める.
        //今回は障害物のみ考慮した方向決定.

        //障害物回避考慮.
        float dir = g_obsAvoidDir;

        //0～L_2PIの範囲に入るように調整.
        while( (dir < 0.000f) || (dir > L_2PI) ){
            dir = ADJUST_RAD( dir );
        }

        //方向を更新.
        selfDir = ADJUST_RAD( selfDir + dir );

        //位置を更新.
        selfPos.x += selfVel * cosf( selfDir );
        selfPos.y += selfVel * -sinf( selfDir );
    }
}

視野や分離周りのパラメータは，状況に応じて調整するものである．
視野範囲を大きくしたり，視野を広げたりすれば，群れができやすくなる．
分離範囲を大きくしたり，最大分離角度を180度に近づければ，群れが分かれやすくなる．

また，視野内にBoidがいない場合の行動において，
プレイヤーを追う，といったことをさせれば，
そのBoidがリーダー的存在となって群れが行動するようになる．

上記サンプルは，コメントアウトしてある箇所を埋めれば，
ある程度ちゃんと動くはず．

注意

角度計算

上記サンプルの中で，以下のようなコードがある．

float GetRotateRad( const float from, const float to )
{
    //角度候補1.
    const float dir1st      = ( to - from );
    const float dir1stVal   = fabsf( dir1st );

    //角度候補2.
    const float dir2ndVal   = ( L_2PI - dir1stVal );
    const float dir2nd      = ((dir1st>=0.0f)?-1.0f:1.0f) * dir2ndVal;

    //絶対値が小さい方を採用.
    return ( dir1stVal > dir2ndVal ) ? dir2nd : dir1st;
}

これは，累積値を計算する際に，角度が大きい方を採用していると，
計算結果がおかしくなる，という現象を防ぐために行っている．

例えば，自分から見て30°方向と-30°方向にBoidがいた時に，
本来なら( 30 + (-30) ) / 2 = 0°となるはずが，
( 30 + 330 ) / 2 = 180°と計算してしまうバグを防ぐ効果がある．

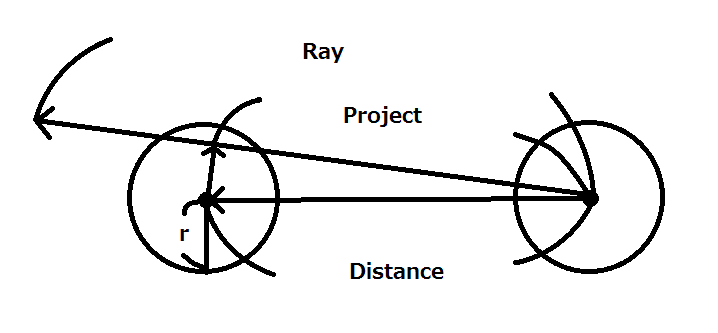
障害物計算

コードだとちょっとわかりづらいので，以下のイメージを参照してもらいたい．
やっていることは比較的単純なことである．

動作状況

手元のビジュアライザーで動作確認をしてみた．
障害物や周りのBoidを気にしながら，群れ行動をしていることはわかると思う．
(使っている画像は大昔にWeb上から拾ってきたものである．ライセンス的にまずいなどを知っている方がいたら教えてほしい．)
(ざっと調べた感じだとFirst Seed Materialさんのものらしいがサイトは閉鎖，または移動したとのこと．)

総括

仕組みは非常に単純ながら，群れ行動をしっかりシミュレートできていて,
とても感動する．動いている状態をボーッと見ているだけでも楽しい．
このままゲームに実装されていることもあるらしいので，
単純ながら非常に強力なアルゴリズムだと思われる．
最高．