【ゲームAI】A*アルゴリズム＋影響マップ

#概要
ゲームAIに関して勉強し始めたので，その備忘録．
本記事では，グラフ上の最良経路を算出するA*アルゴリズムと，
ノードに動的な重み付けを行う影響マップについて記述する．

本記事は【ゲームAI】基本的な経路探索のウェイポイントナビゲーションの続きとなる．
ウェイポイントナビゲーションについて知っている方は見なくてよいが，
知らない方は軽く見ておくと良いかもしれない．

#参考
ありきたりではあるが以下の書籍を用いた．
ゲーム開発者のためのAI入門

また，以下のサイトがとても分かりやすい，且つ実践的だと思う．
ゲームAI -基礎編- 『知識表現と影響マップ』

#事前準備
ベクトル計算用の構造体，便利関数の準備と，
角度計算用のマクロの準備を行う．

//角度計算用マクロ.
#define L_PI		(3.1415f)
#define L_2PI		(6.2830f)
#define L_H_DEG		(180.0000f)
#define L_DEG		(360.0000f)
#define DEG2RAD(e) ((e)*(L_PI)/(L_H_DEG))
#define RAD2DEG(e) ((e)*(L_H_DEG)/(L_PI))
#define ADJUST_RAD(e) (((e)<(0.0000f))?(e)+(L_2PI):((e)>(L_2PI))?(e)-(L_2PI):(e))
#define ADJUST_DEG(e) (((e)<(0.0000f))?(e)+(L_DEG):((e)>(L_DEG))?(e)-(L_DEG):(e))

#define CLIP(e,l,h) (min(max(e,l),h))

//ベクトル構造体.
#define VECTOR SVector2D<float>
template <class T>
struct SVector2D
{
	typedef T DataType;
	T x;
	T y;
	SVector2D(){ Init(); }
	void Init()
	{
		x = T();
		y = T();
	}
	SVector2D	operator +  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x + e.x; tmp.y = y + e.y; return tmp; }
	SVector2D&	operator += ( const SVector2D& e ){ x += e.x; y += e.y; return (*this); }
	SVector2D	operator -  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x - e.x; tmp.y = y - e.y; return tmp; }
	SVector2D&	operator -= ( const SVector2D& e ){ x -= e.x; y -= e.y; return (*this); }
	T			operator *  ( const SVector2D& e ) const { return ( x * e.x ) + ( y * e.y ); }
	SVector2D&	operator *= ( const int e ){ x *= e; y *= e; return (*this); }
	SVector2D&	operator *= ( const float e ){ x *= e; y *= e; return (*this); }
	SVector2D&	operator /= ( const int e ){ x /= e; y /= e; return (*this); }
	SVector2D&	operator /= ( const float e ){ x /= e; y /= e; return (*this); }
};

//数学関連の関数群.
namespace LMath
{
	VECTOR::DataType GetScalar( VECTOR vec )
	{
		return sqrtf( vec.x * vec.x + vec.y * vec.y );
	}

	VECTOR Normalize( VECTOR vec )
	{
		const VECTOR::DataType vecLen = GetScalar( vec );
		vec.x /= vecLen;
		vec.y /= vecLen;
		return vec;
	}

	VECTOR Normalize( VECTOR from, VECTOR to )
	{
		VECTOR tmp = to - from;
		return Normalize( tmp );
	}

	float GetRotateRad( const float from, const float to )
	{
		//角度候補1.
		const float dir1st		= ( to - from );
		const float dir1stVal	= fabsf( dir1st );

		//角度候補2.
		const float dir2ndVal	= ( L_2PI - dir1stVal );
		const float dir2nd		= ((dir1st>=0.0f)?-1.0f:1.0f) * dir2ndVal;
			
		//絶対値が小さい方を採用.
		return ( dir1stVal > dir2ndVal ) ? dir2nd : dir1st;
	}

	bool IsCollisionCircle( const VECTOR& pos1, const VECTOR& pos2, const float r )
	{
		VECTOR tmp = pos1 - pos2;
		return ( GetScalar( tmp ) < r );
	}
};

また，今回は優先度付きキューを使用する必要があるので，バイナリヒープも用意しておく．

namespace Util
{
	enum BH_COMP_TYPE
	{
		BH_COMP_TYPE_MIN = 0,
		BH_COMP_TYPE_MAX,
		BH_COMP_TYPE_NUM,
		BH_COMP_TYPE_INVALID = -1,
	};
	static bool IsValid( BH_COMP_TYPE e ){ return ( 0 <= e && e < BH_COMP_TYPE_NUM ); }

	template<class T>
	class BinaryHeap
	{
	public:
		typedef T DataType;

	public:
		BinaryHeap() : m_type( BH_COMP_TYPE_INVALID ), m_buf( NULL ), m_size( 0 ), m_count( 0 ){}
		~BinaryHeap(){}

	public:
		void Init( BH_COMP_TYPE type, const int size )
		{ 
			m_type	= type; 
			m_buf	= new T[size]; 
			m_size	= size;
			m_count = 0;
		}
		void Term(){ if( m_buf ){ delete [] m_buf; m_buf = NULL; } }
	
	public:
		void Push( T e )
		{
			if( IsFull() ){ return; }
			int self = m_count;
			while( self > 0 ){
				const int parent = ( self - 1 ) / 2;		//親.
				if( !bComp( e, m_buf[parent] ) ){ break; }	//親の方が上にくるべきなら終了.
				m_buf[self] = m_buf[parent];				//親を移動.
				self = parent;								//自分を親の位置に移動.
			}
			m_buf[ self ] = e;
			m_count++;
		}
		bool bPop( T& e )
		{
			if( IsEmpty() ){ return false; }
			e			= m_buf[0];
			m_buf[0]	= m_buf[--m_count];
			int self	= 0;
			while( self < m_count ){
				const int child1 = ( self * 2 ) + 1;
				const int child2 = ( self * 2 ) + 2;
				int next = self;
				if( child1 < m_count ){ if( bComp( m_buf[child1], m_buf[next] ) ){ next = child1; } }
				if( child2 < m_count ){ if( bComp( m_buf[child2], m_buf[next] ) ){ next = child2; } }
				if( next <= self ){ break; }
				T tmp = m_buf[self];
				m_buf[self] = m_buf[next];
				m_buf[next] = tmp;
				self = next;
			}
			return true;
		}

	private:
		bool bComp( const T& child, const T& parent )
		{
			switch( m_type )
			{
			case BH_COMP_TYPE_MIN:	return ( child < parent );
			case BH_COMP_TYPE_MAX:	return ( child > parent );
			default:	return false;
			}
		}

	public:
		bool IsFull() const { return ( m_count >= m_size ); }
		bool IsEmpty() const { return ( m_count <= 0 ); }

	private:
		BH_COMP_TYPE	m_type;
		T*				m_buf;
		int				m_size;
		int				m_count;
	};
};

#A*アルゴリズム
##概要
グラフ探索の原理としては，ダイクストラアルゴリズムと同じであるが，
コストの扱い方が少し特殊になっている．
(ダイクストラ法：http://www.deqnotes.net/acmicpc/dijkstra/)

本来，ダイクストラアルゴリズムでは，ノード間のエッジコストを元に最短経路を算出する．
すなわち以下の式が成り立つ．
cost = edgeCost

しかしながら，A*アルゴリズムではエッジコストにヒューリスティックコストを加えたものをコストとして扱う．
すなわち以下の式のようになる．
cost = edgeCost + heuCost

A*アルゴリズムはヒューリスティックコストが入る関係上，
最短経路探索アルゴリズムではなく，最良経路探索アルゴリズムとなる．

##ヒューリスティックコスト
ヒューリスティックとは，心理学においては「経験則」を指し，
計算機科学においては「精度保証のない近似解」を指す．
根本的な部分は同じことを表しており，「直感や経験に基いて精度の高い解を示すこと」である．

つまりヒューリスティックコストとは，
経路計算用コストとしてぱっとみ正しそうなコストのことである．

A*アルゴリズムでは，最短経路を計算する場合に，
目標地点と自分を繋いだ直線距離をヒューリスティックコストとして扱うことが多い．
目標地点から遠いノードは，ぱっとみ最短経路ではなさそうだし，
目標地点に近いノードは，ぱっとみ最短経路っぽいからだ．
しかしながら，間に障害物があって通れない，道が途絶えている，など
目標地点に近いからといって最短経路になるわけではない．

ヒューリスティックコストは，目的に応じた正確なコストを選択できれば，
最良経路探索の一助となってくれる．
ゲームAIにおいては，明らかに危険な道を突っ切るAIよりも，
多少遠回りでも安全な道を行くAIの方が賢く見える，といったことがあるので，
最良経路探索は相性が良い．

##影響マップ
ゲームでは，敵との距離，敵の視野範囲など，ヒューリスティックコストとして使用できる情報は多い．
しかし，これらの情報はゲーム中に変動するものが多いため，事前にノードに設定しておいたものを用いることはできない．
(もちろん，情報の種類によっては，事前に設定したものを用いることはできる．)
(俗に，静的，焼き付けと呼ばれる手法は，事前に計算してデータを保持しておくことを指す．)

そこで，ゲーム状況に合わせて動的にヒューリスティックコストを設定しよう，というのが，影響マップである．

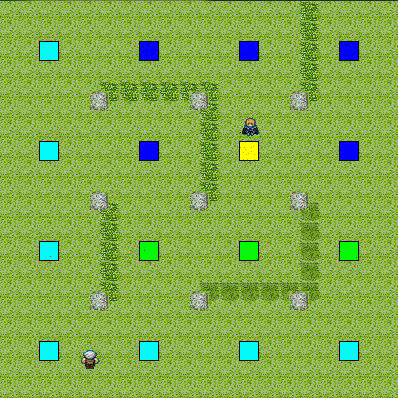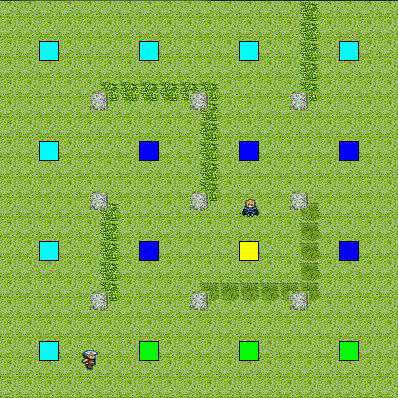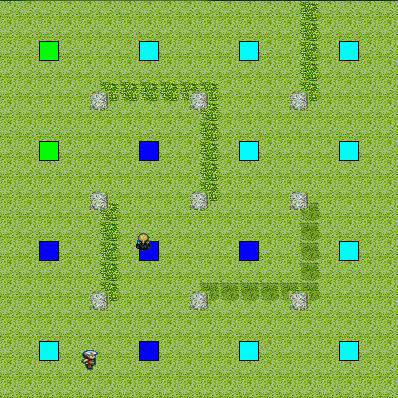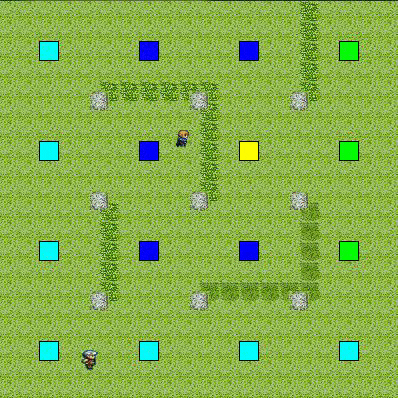
以下に例を挙げる．赤に近いノードはコストが高く，青に近いノードはコストが低い．

目標との距離
(目標に近い地点ほどコストが低く，遠い地点ほどコストが高い)

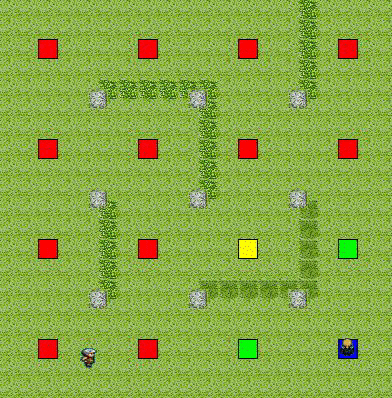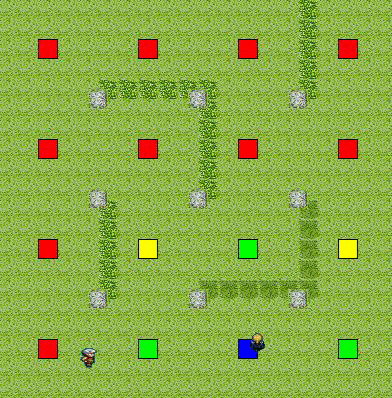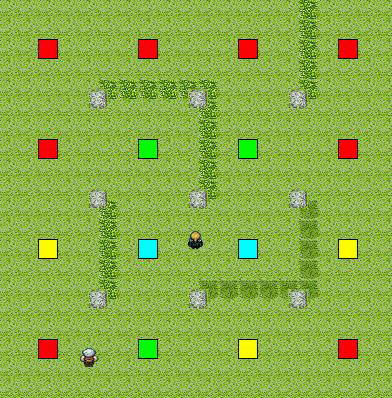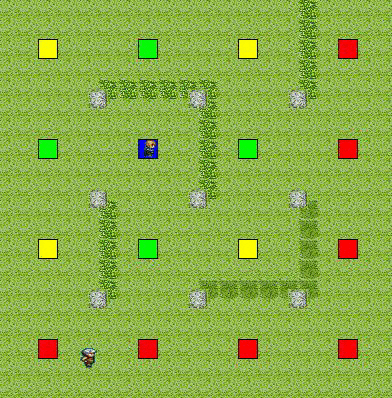
目標の視野範囲
(視野範囲に入っている地点ほどコストが高く，外れている地点ほどコストが低い)

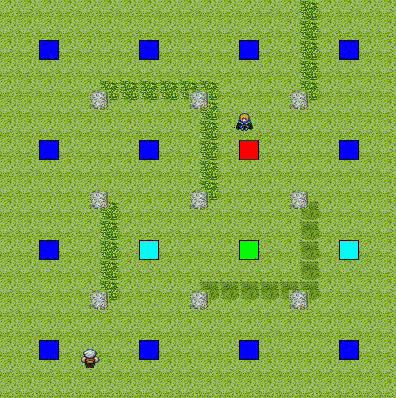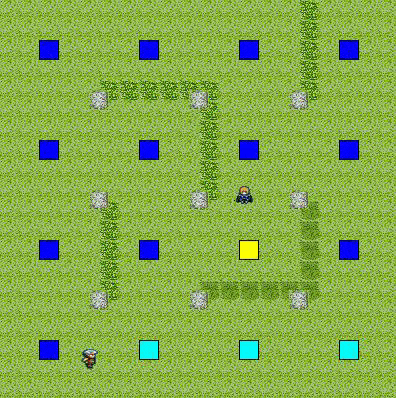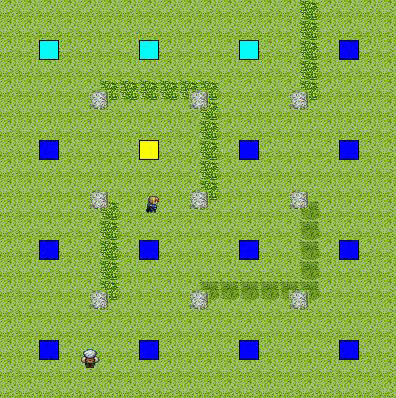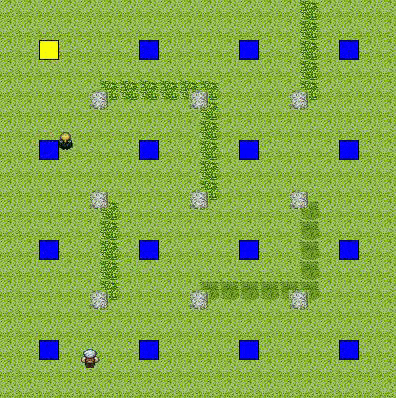
上記二例を合成したもの
(視野に入っている所はコストが高めだが，死角はとても低い．距離が離れると一定のコストとなる．)
(合成比率は，距離が30%，視野範囲が70%)

##実装
影響マップを使用したA*アルゴリズムの実装を以下に示す．

const int WAY_POINT_MAX_NUM = 20;
const float INF_COST = (1 << 29); 

enum INFLUENCE_MAP_TYPE
{
	INFLUENCE_MAP_TYPE_DIST = 0,
	INFLUENCE_MAP_TYPE_VIEW,
	INFLUENCE_MAP_TYPE_NUM,
	INFLUENCE_MAP_TYPE_INVALID = -1,
};
static bool IsValid( INFLUENCE_MAP_TYPE e ){ return ( 0 <= e && e < INFLUENCE_MAP_TYPE_INVALID ); }

//ヒューリスティックコスト取得.
//(ヒューリスティックコストはすでに計算済み想定).
float g_influenceMap[ INFLUENCE_MAP_TYPE_NUM ][ WAY_POINT_MAX_NUM ];
float GetHeuCost()
{
	float tmp = 0;
	tmp += g_influenceMap[INFLUENCE_MAP_TYPE_DIST][n] * 0.3f;
	tmp += g_influenceMap[INFLUENCE_MAP_TYPE_VIEW][n] * 0.7f;
	return tmp;
}

//最短経路計算.
//(g_edgeWeightはノードが繋がっていることを表している．設定済み想定．地形などに応じてコストを設定する場合は，ここを調整する).
float g_shortestPath[WAY_POINT_MAX_NUM][WAY_POINT_MAX_NUM];
float g_edgeWeight[WAY_POINT_MAX_NUM][WAY_POINT_MAX_NUM];
void UpdateShortestPath( const int startNode, const int endNode )
{
	//初期化.
	for( int i = 0; i < WAY_POINT_MAX_NUM; ++i ){
		for( int j = 0; j < WAY_POINT_MAX_NUM; ++j ){
			g_shortestPath[i][j] = INF_COST;
		}
	}

	//データ.
	struct SData
	{
		int nodeIndex;
		float cost;
		SData(){ Init(); }
		void Init(){ nodeIndex = -1; cost = 0.0f; }
		bool operator < ( const SData& e ) const { return (cost) < (e.cost); }
		bool operator > ( const SData& e ) const { return (cost) > (e.cost); }
	};

	//キューを用意.
	Util::BinaryHeap< SData > queue;
	queue.Init( Util::BH_COMP_TYPE_MIN, WAY_POINT_MAX_NUM );

	//A*.
	{
		g_shortestPath[startNode][startNode] = 0;

		//始点を入れてスタート.
		SData start; 
		start.nodeIndex = startNode;
		start.cost = 0;
		queue.Push( start );

		while( !queue.IsEmpty() ){
			SData s;
			if( !queue.bPop( s ) ){ continue; }

			for( int i = 0; i < WAY_POINT_MAX_NUM; ++i ){
				if( s.nodeIndex == i )							{ continue; }	//自分.
				if( g_edgeWeight[s.nodeIndex][i] >= INF_COST )	{ continue; }	//辺がつながっていない.
				if( g_shortestPath[i][i] < INF_COST )			{ continue; }	//すでに訪れている.

				g_shortestPath[i][i] = s.cost + g_edgeWeight[s.nodeIndex][i] + GetHeuCost( i );

				SData d;
				d.nodeIndex = i;
				d.cost		= g_shortestPath[i][i];
				queue.Push( d );
			}
		}
	}

	//経路復元.
	{
		int goal = endNode;
		while( goal != startNode ){
			bool bSuccess = false;

			for( int i = 0; i < WAY_POINT_MAX_NUM; ++i ){
				if( goal == i )							{ continue; }	//自分.
				if( g_edgeWeight[i][goal] >= INF_COST )	{ continue; }	//辺がつながっていない.

				const float startCost = g_shortestPath[goal][goal] - ( g_edgeWeight[i][goal] + GetHeuCost( goal ) );
				if( abs( g_shortestPath[i][i] - startCost ) < 0.001f ){
					//一つ前のノードを発見したので，最短パス用のバッファに記録しておく.
					g_shortestPath[i][goal] = g_edgeWeight[i][goal];
					goal		= i;
					bSuccess	= true;
					break;
				}
			}

			if( !bSuccess ){ break; }	//次のノードが発見できなかったので，無限ループ防止で抜ける.
		}
	}

	queue.Term();
}

//次のノードを取得する.
int GetNextNode( const int s, const int e )
{
	for( int i = 0; i < WAY_POINT_MAX_NUM; i++ ){
		if( i == s ){ continue; }
		if( g_shortestPath[s][i] < INF_COST ){
			return i;
		}
	}
	return -1;
}

##注意
影響マップは，1マップに対して，1要素に関するコストのみ入れるようにした方が良い．
調整時やデバッグ時に，何がどれくらい影響しているかが一目瞭然だからだ．

経路復元に関しては，かなり適当に作ったので，正しく動かないケースもあると思われる．
正しい実装を知りたい場合は，google先生に質問してください．

##動作状況

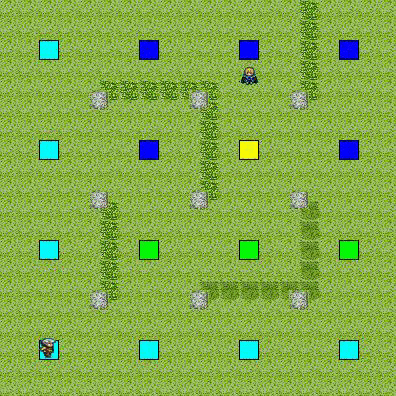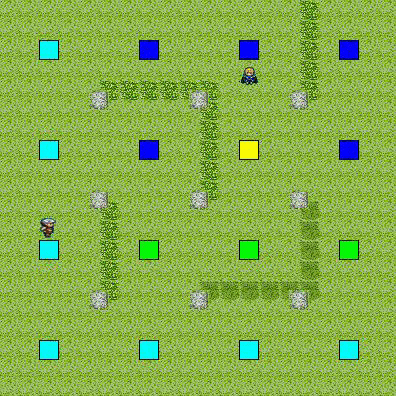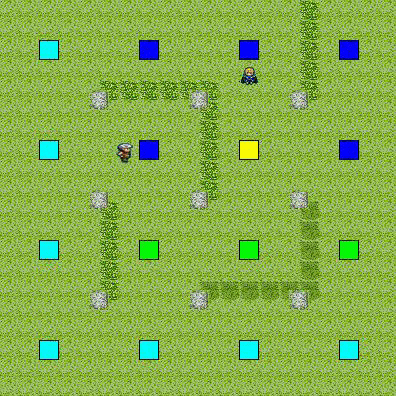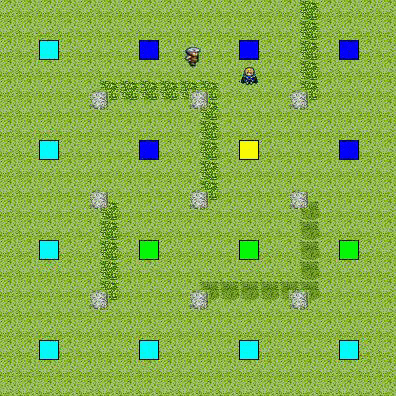
目標の視野に入らないルートで，最短経路を移動していることがわかる．
単純に最短経路を移動して，相手の正面から突っ込んでしまうよりも多少賢く見える．

#総括
賢いAIを作るに当たって，様々な要因を鑑みた経路探索を行うことは重要であり，
その点において，影響マップは非常に有用な手法である．
A*アルゴリズム，影響マップ共に，良く用いられる手法であるので，知っていて損はないと思う．