画像解析実践入門_指紋の稜線分析 2(スケルトン化とラベリング)

の続きです。

#概要　
指紋の稜線を分析します。前回の記事で画像の二値化までしました。
最終的にはこの二値指紋画像をサブ領域に分割して、そこから特徴量(今回は稜線角度)を抽出。
指紋認識が可能か検討してみます。

もくじ

• 1.二値画像のスケルトン(細線)化処理
• 2.画像をサブ領域に分割
• 3.サブ領域ごとに稜線をラベリング

#1.二値画像のスケルトン(細線)化処理
前回の記事で指紋画像を二値化しました

この二値画像から稜線の情報を解析していきたいのですが、その際に白の線(解析対象)の持つ__「線幅」は正直余計な情報__と言えます。
この指紋の解析において意味を持つ情報は連結成分の中心線つまり__解析対象の「骨格」__になります。
そういうう場合はオブジェクトの連結情報を崩さずに境界を侵食していく処理,スケルトン化,細線化
がおすすめです。

スケルトン化について
https://scikit-image.org/docs/dev/auto_examples/edges/plot_skeleton.html

ではスケルトン化処理を二値画像に適応してみましょう。

skeletonize.py

from skimage.morphology import skeletonize
#画像のスケルトン化
skelton_img = skeletonize(bin_locla)
plt.imshow(skelton_img,cmap='gray')
skelton_img.shape #(90,90)

スケルトン化できました。次は画像を解析エリアごとに分割して行きます。

#2.画像をサブ領域に分割
画像を分割して、その領域ごとに特徴量を計算します。今回は5*5に分割します。

crop.py

#画像のサイズと分割時のサイズを計算する
H,W=skelton_img.shape
#5*5の領域に分割します
crop_num =5
#クロップ領域の画像の縦横を計算します。
h_crop=int(skelton_img.shape[0]/crop_num)
w_crop=int(skelton_img.shape[1]/crop_num)
print(H,W,h_crop,w_crop) #90,90,18,18
#分割してリストで保存
croped_imgs = [skelton_img[h_crop * x:h_crop * (x+1), v_crop * y:v_crop * (y+1)] for x in range(crop_num) for y in range(crop_num)]

参考にした記事
https://tomomai.com/python-opencv-numpy/

分割した画像はリスト配列で保存したのでfor文で取り出してプロットして見ましょう。

plt_crop_img.py

plt.figure(figsize=(10,10))
plt.subplots_adjust(wspace=0.1, hspace=0.1)
#画像を取り出して表示
for i in range(len(croped_imgs)):
    ax = plt.subplot(crop_num,crop_num,i+1)
    plt.imshow(croped_imgs[i],cmap='gray')
    plt.axis('off')

#3.サブ領域ごとに稜線をラベリング
稜線のラベリング処理を行います。二値画像の中に存在する連結成分にラベル付を行うことで稜線同士を比較することが可能となります。

ラベリング処理関数について
https://scikit-image.org/docs/dev/api/skimage.measure.html#skimage.measure.label

lable.py

#サブ領域ごとにラベリング
from skimage.measure import label
labeld_imgs = [label(croped_imgs[i]) for i in range(len(croped_imgs))]

#ラベリング結果を表示
plt.figure(figsize=(10,10))
plt.subplots_adjust(wspace=0.1, hspace=0.1)
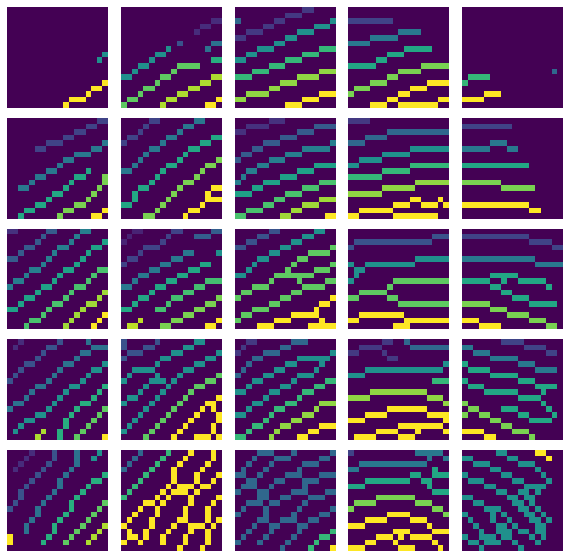
for i in range(len(labeld_imgs)):
    ax = plt.subplot(crop_num,crop_num,i+1)
    plt.imshow(labeld_imgs[i])
    plt.axis('off')

ラベリングが完了しました。
右下5行5列目などが誤連結でラベル数少ないですが、とりあえず良しとしましょう。
一応ラベリングされた画像の画素を直接見てみましょう。

num.py

labeld_imgs[2]#1行目３列目の画像

       [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0],
       [2, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 3],
       [0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 3, 3, 3, 0],
       [0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 3, 3, 3, 0, 0, 0, 0],
       [1, 1, 0, 0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 3, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 4],
       [0, 0, 3, 3, 0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 4, 0, 0, 0],
       [3, 3, 0, 0, 0, 0, 0, 0, 0, 4, 4, 4, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 4, 4, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 4, 4, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, 5],
       [4, 4, 4, 0, 0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 5, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 5, 5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 6, 6],
       [5, 5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 6, 6, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 6, 6, 0, 0, 0, 0, 0, 0],

連結している画素が同じラベル値として1~6ラベルが含まれていることがわかります。

#まとめ
今回は二値画像から細線化処理、ラベリングまでを行いました。
次回からこのラベリング画像を用いて稜線間隔と稜線方位を解析します。
これまではskimageのモジュールを利用してかなり楽をしています。
次回からアルゴリズムに基づいて本格的に解析用のコードを記述していきますのでお楽しみに。

ちなみに参考としている書籍「MATLAB画像処理入門」と同著者,同内容、の論文が
高井 信勝: 稜線方位分布による指紋のコード化
[http://hokuga.hgu.jp/dspace/bitstream/123456789/2093/1/%E8%AB%96%E6%96%8713.pdf]
に掲載されています。ご参考までに。

続きです