この記事の内容
C++17でLegendre関数を使ってみる。でLegendre関数の実装についてアドバイスをもらったのでそれをSnap.svgを使ってSVGでグラフを書くを使って確かめてみる。
Legendre関数の実装
const coff=[];
function calc_coff(n){
for( let i=0; i<=n; i++ ){
if( coff[i]!==void 0 ) continue;
const arr=[];
for( let m=0; m<=i; m++ ){
if( m%2!==i%2 ){ arr.push(0); continue }
let val=1.0;
for( let j=1, max=(i-m)/2; j<=max; j++ ) val/=j;
for( let j=(i+m)/2+1, max=i+m; j<=max; j++ ) val*=j;
for( let j=1; j<=m; j++ ) val/=j;
val/=Math.pow(2.0, i);
if( ((i-m)/2)%2==1 ) val*=-1;
arr.push(val);
}
coff.push(arr);
}
}
export default function(n, x){
if( coff[n]===void 0 ) calc_coff(n);
let val=coff[n][n]*x+coff[n][n-1];
for( let i=n-2; i>=0; i-- ) val=val*x+coff[n][i];
return val;
}
以前の実装、係数を計算してそこから実際の計算。係数自体は一度計算するとメモリに保存される。(あがいた後としてhorner法の実装が残ってる...。)
export default function(n, x){
if( n===0 ) return 0;
if( n===1 ) return x;
if( x===1 ) return 1;
else if( x===-1 ) return n%2===1 ? -1 : 1;
let val=0, val_n=x, val_n1=1;
for( let i=2; i<=n; i++ ){
val=2*x*val_n-val_n1-(x*val_n-val_n1)/i;
val_n1=val_n;
val_n=val;
}
return val;
}
新しい実装、かなりすっきりした。コメントでもらった実装とほぼ同じ。
index.htmlとentry.js
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<link rel="stylesheet" type="text/css" href="css/graph.css">
<title>Math by Javascript</title>
<script src="lib/Snap.svg-0.5.1/dist/snap.svg-min.js"></script>
<script src="node_modules/mathjax/MathJax.js?config=TeX-AMS_CHTML"></script>
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
displayAlign: "left",
displayIndent: "2em"
});
</script>
<script src="dist/legendre_sample.js"></script>
</head>
<body>
<h1>JavascriptとSnap.svgでLegendre関数を書く</h1>
<form>
n : <input id="legendre_n" type="Number" min="0" max="100", step="1", value="10">:
<button id="draw" type="button">描画</button>
<button id="draw_all" type="button">すべて描画</button>
</form>
<div id="canvas">
</div>
</body>
</html>
import $ from 'jquery'
import { svg } from '../src/svg.js'
import { math } from '../src/math.js'
$(()=>{
console.log('===== Graph Sample =====');
const max_range=100;
const canvas=svg.make.top('#canvas');
const graph=canvas.graph(0.1, 0.1, 0.95, 0.95);
graph.set_range(-1.0, 1.0, -1.0, 1.0);
math.func.legendre(10, 0);
draw();
function draw(){
const n=parseInt($('#legendre_n').val());
graph.draw((x)=>{ return math.func.legendre(n, x)});
}
function draw_all(){
const n=parseInt($('#legendre_n').val());
graph.draw((x)=>{ return math.func.legendre(n, x)});
for( let i=1; i<n; i++ ){
graph.add((x)=>{ return math.func.legendre(i, x)});
}
}
$("#draw").click(()=>{ draw(); })
$("#draw_all").click(()=>{ draw_all(); })
});
前とほぼ同じ、legendreは$(x, y)$ともに$[-1:1]$に収まるので範囲は固定した。
比較
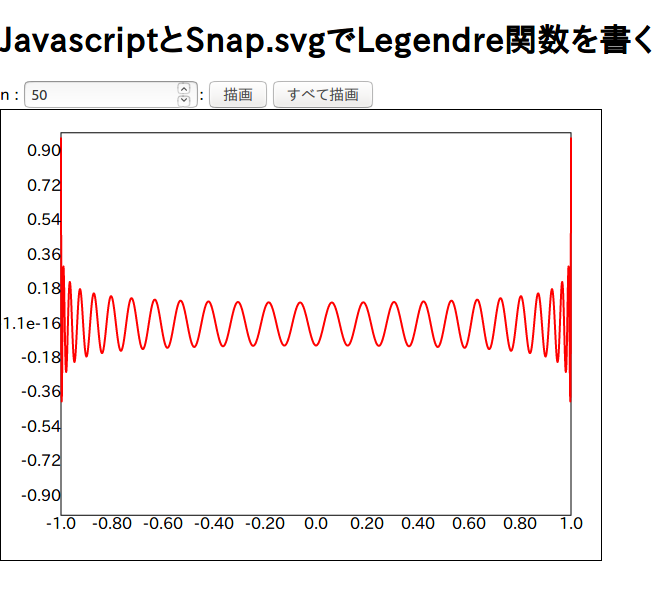
新しい実装
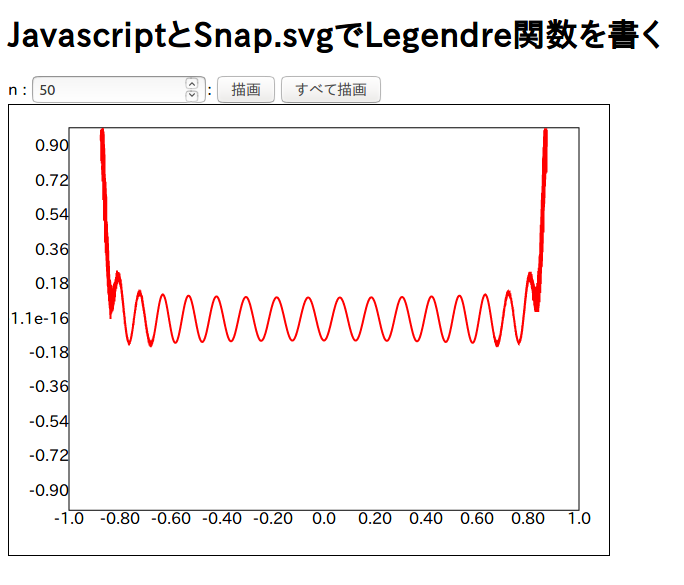
古い実装
見た目的には40ちょっと前からガタつきだして40を超えると完全に1の付近は合わなくなる。50になると上のように一目瞭然である。
新しい実装ではn=100まで綺麗に書けた。
感想
数値計算だとやっぱり手元ですぐにグラフ化できる環境は大切である。C++でもグラフ化する環境はあるがサボってた。
ひとつの関数を書かせるのに100000回計算させているが一本なら大して遅いとは感じなかった。流石に全部で100とかやると体感は待たされる(多分、1分はかかっていない)。それよりも画面をスクロールした時のレンダリングが追いつかなくなった...。
描画点は今かなり多くとっているので下げても良いかも、最速を目指すんだとかいう目的でなければこの方法がベストだと思います。
一応、最速を求めるなら、結局激しく振動している部分を遠い点で評価してるのが多分問題なので、多項式の係数までも止まっているので適当な点(近い点)でテーラー展開してしまえば精度は上がるはずです(テーラー展開を計算するときの桁落ちとかの問題はあります)。
パラメーターはC++17でLegendre関数を使ってみるのように事前に計算しておいてマップ化しておけば実行時の計算速度は向上するはずです。
ついでだからLegendreの陪多項式も
P^m_l(x)=\frac{(2l-1)xP^m_{l-1}(x)-(l+m-1)P^m_{l-2}(x)}{l-m} \\
P^m_{m-1}(x)=0 \\
P^m_m(x)=(2m-1)!!(1-x^2)^{\frac{m}{2}}
で計算できます。$!!$は2乗階乗で一つ飛ばしの階乗です。C++のコードは何故か$(1-x^2)^{\frac{m}{2}}$を因数分解して$\left(\sqrt{(1-x)}\sqrt{(1+x)}\right)^m$として計算していました。コメントでそのほうが精度が上がると書いていました。実装はちょっと読みづらかったので上の式に従って計算させました。
export default function(l, m, x){
const absm=Math.abs(m);
if( l<absm ) return 0;
let val_m1=0, val_m=init_val(absm, x);
if( l===absm ){
if( m>=0 ) return val;
else return m(l, m, val);
}
let val=(2*absm+1)*val_m;
for( let i=absm+1; i<=l; i++ ){
val=((2*i-1)*x*val_m-(i+m-1)*val_m1)/(i-m);
val_m1=val_m;
val_m=val;
}
if( m>=0 ) return val;
else return m(l, m, val);
}
function m(l, m, val){
if( m%2===1 ) val*=-1;
for( i=l-m; i>0; i++ ) val*i;
for( i=l+m; i>0; i++ ) val/m;
return val;
}
function init_val(m, x){
let val=1;
for( let i=2*m-1; i>0; i-=2 ) val*=i;
val*=Math.pow(1-x, m/2)*Math.pow(1+x, m/2);
return val;
}
JavaScriptの実装、初期値計算と符号反転部分は関数化した。パラメーターが増えた分、長くなってこちょこちょいじる部分が出てきた。
一応、$P^0_l(x)$がLegendre関数になるのでそれで確認したが$m=0$のみの確認なので何かバグがあるかも...。
ルジャンドルの陪多項式といえば正規化して位相$e^{im\phi}$をかければ球面調和関数になるので余裕があればthree.jsを使って3次元的に描いて見るかもしれません。
その前に数値積分を使って直交性を確かめて更に実装の確認を進めるべきかな?