更新点
- 2024/7/23
再帰関数への対処例として、functools.cacheを利用した処理を追加しました
前書き
例のごとく色々と勉強していたところ、動的計画法に出会いました。以前から存在だけは認知していたのですが、いざ読んでみたら何もわかっていないことがわかったので、ここで自分用にまとめておきます。せっかくなので、似た部分がある再帰処理と併せて確認していきます。
再帰処理
概要
ある手続きの中で、自分自身への呼び出しが含まれる処理を再帰処理といいます。手続きはプロシージャ、自分自身を呼び出すことは再帰呼び出しと呼ばれることもあります。
再帰処理の特徴は、大きな問題を分割し小さな問題にしたうえで、それが解決されるまで処理を繰り返すというものです。Pythonでは基本的には再帰処理を含む関数、再帰関数として実装されることになります。
階乗を求める関数の例
例として、階乗を求める関数を作ってみましょう。
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
assert factorial(3) == 6
再帰関数は基本的に、ベースケースと再帰ケースの2つから構成されています。
ベースケースは再帰呼び出しが終了する=具体的な値がreturnしてくる部分のことです。
if n == 0:
return 1
再帰ケースはその名の通り、再帰処理が発生する部分です。
else:
return n * factorial(n - 1)
再帰処理にあまり慣れていないと、関数の定義の中で、その関数自身が呼び出されていることに大きな違和感を覚えるでしょう。実際私も、以前再帰処理に出会ったときは、全く理解できなかった覚えがあります。
このような定義が行われた部分は具体的な値が返ってくるまで、繰り返し自身を呼び出し続けることになります。
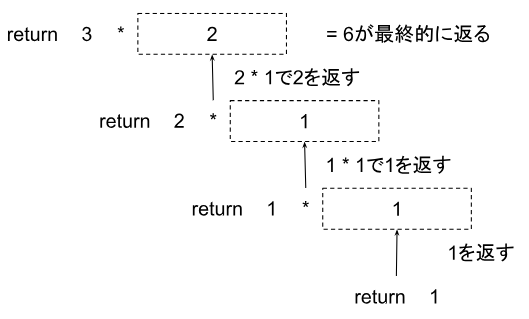
図にすると以下のような感じです。
1がreturnされた後は、その後はちょうど折り返すように値が返ってきます。
これが再帰関数です。何かしらの値がreturnされてくるまで再帰呼び出しを行い、それが終わった後は溜まっていた(スタックしていた)処理を順番に行っていくことになります。
フィボナッチ数を求める関数
次の例として、フィボナッチ数列を利用してみます。フィボナッチ数列は初めが0,次は1,以降は手前2つの和が次になるという数列です。
\displaylines{
f(0) = 0 \\
f(1) = 1 \\
f(n) = f(n-1) + f(n-2) \qquad (n \geq 2)
}
順番に計算することで、任意の番号のフィボナッチ数を求めることが可能です。
\displaylines{
f(2) = f(1) + f(0) = 1 \\
f(3) = f(2) + f(1) = 2 \\
f(4) = f(3) + f(2) = 3 \\
}
ここで、初項を0番と定義した際に、n番目のフィボナッチ数を再帰関数を使って求めると以下のようになります。
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
assert fibonacci(4) == 3
動作自体はシンプルです。
ベースケースは、
if n == 0:
return 0
elif n == 1:
return 1
のところです。n=0であれば0を、n=1であれば1を返します。
再帰ケースは、
return fibonacci(n - 1) + fibonacci(n - 2)
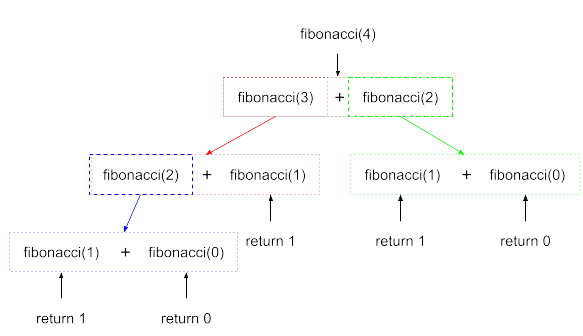
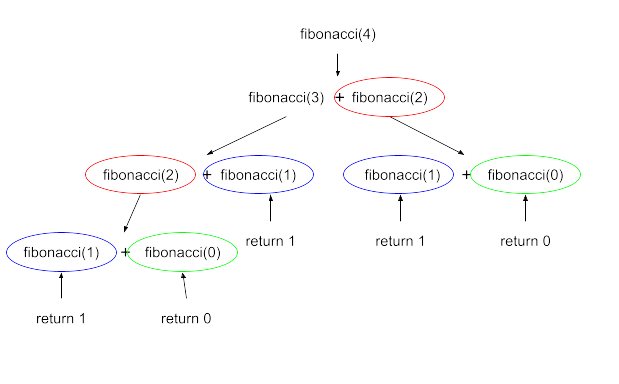
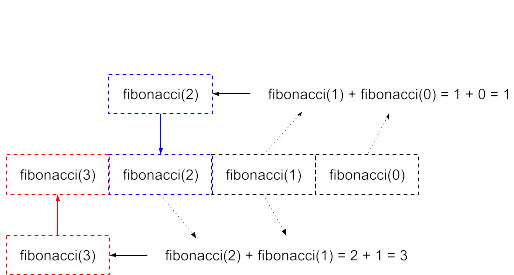
の部分です。すこし分かりづらいので、実際にn=4のときの呼び出しを図にすると、以下のような動作になります。
4からは3と2が、3からは2と1が……といった具合に、具体的な値が返ってくるまで、つまりn=0かn=1になるまで延々と呼び出しが続きます。
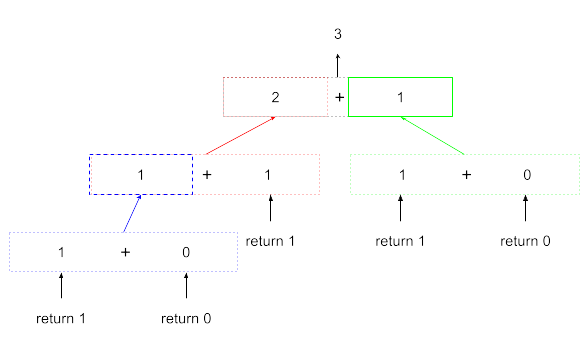
折り返してくる値の流れは以下のようになります。
順番に呼び出して、ベースケースから値が返ってきた結果、答えは3となります。実際に、0, 1, 1, 2, 3がn=4までのフィボナッチ数列なので、3は正しい値です。
再帰関数の欠点
以上のように、階乗を求める関数もフィボナッチ数を求める関数も、とりあえず動きます。しかし、実はこれらの関数には、それぞれ欠点があります。
階乗を求める関数の欠点
階乗を求める関数の欠点ですが、これは再帰の呼び出しが深くなりすぎると、制限にひっかかってしまうことになります。
基本的にプログラムでは、変数の代入や関数の操作など、何かを行う度にスタックメモリと呼ばれる計算領域を消費していきます。
通常であれば、不要になったタイミングで順次メモリが解放されますが、再帰呼び出しは全ての計算やreturnが繋がっています。
結果として、スタックメモリが消費され続けて、スタックオーバーフローが発生し、プログラムが停止してしまいます。さらに悪いと、インタープリター自体がクラッシュしてしまうこともあります。
これを防ぐため、再帰呼び出しの深さは、通常はシステム側か言語側に呼び出し制限の深さが設定されています。階乗を求める関数は、これに簡単にひっかかってしまいます。
print(factorial(3000))
RecursionError: maximum recursion depth exceeded
一応、Pythonでは、以下のようなコードで再帰の深さの限界を確認し、さらに変更することも可能です。
ただし、仮にインタープリターがクラッシュしなかったとしても、パフォーマンスは低下しますので、安易に変更して乗り切ろうとするのは考えものですね。
import sys
# 確認
print(sys.getrecursionlimit())
# 変更
sys.setrecursionlimit(5000)
フィボナッチ数を求める関数の欠点
フィボナッチ数を求める関数の方の欠点は、数が大きくなると急激に計算時間が増大することです。スペック等にもよるでしょうが、自分のPCでは、n=50の段階で1時間以上かかっていました。
これは再帰処理の構造自体に原因があります。先程上の図で示した通り、基本的にfibonacci(n)からは、fibonacci(n - 1)とfibonacci(n - 2)の2つの呼び出しが発生します。
そこからさらにfibonacci(n - 1)からfibonacci(n - 2)とfibonacci(n - 3)、fibonacci(n - 2)からfibonacci(n - 3)とfibonacci(n - 4)、と合わせて4つの呼び出しが生じます。
これを所定の値まで延々と繰り返すため、時間計算量のオーダーは$O(2^n)$となります。たかだかn=50程度の計算で1時間以上かかったのはこれが原因です。このあとn=51, 52と増やしていくごとに2倍、4倍と途方もない時間がかかることになります。
再帰処理のまとめ
ここで一度、再帰処理についてまとめておきます。まず再帰処理とは、ある手続きの中で自分自身を呼び出す処理のことです。Pythonでは主に関数として実装され、再帰関数と呼ばれます。その再帰関数は自分自身を呼び出す再帰ケースと、呼び出しを停止し、具体的な値を返すベースケースから構成されています。
そしてこの再帰関数には、注意すべき点が2つあります。それが計算時間と再帰呼び出しの深さです。フィボナッチ数を求める関数では、$O(2^n)$の時間計算量が必要となり、計算時間が問題となっていました。一方で階乗を求める関数では時間計算量ではなく、再帰呼び出しの深さの方が問題となっていました
再帰処理自体は、例えばツリー型の構造を持っている場合や、マージソートを行う場合など、有効な場面は数多く存在しています。しかし上記の2つを解消できない場面では、他のアルゴリズムのほうが優れているといえるでしょう。
動的計画法
概要
動的計画法は、大きな問題を小さな問題に分割するという工夫に加えて、一度計算したものを使い回すために記録しておくという工夫が施されたアルゴリズムです。1点目は再帰処理と共通していますが、2点目は動的計画法独自の強みとなります。
動的計画法を用いたフィボナッチ数の算出
ここで、フィボナッチ数を求めるプログラムの問題をもう一度確認しておきましょう。
まず、プログラムは以下のようになっていました。
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
この処理の問題は再帰ケースにあります。一度returnする度に2個の再帰呼び出しを行うので、時間計算量が指数関数的に増加してしまっていました。そもそもの話として、同じ計算を何度も繰り返しているのが非効率さの原因です。
そこで、一度計算したものは再利用できるように記録し、必要があればそこから読み出すことで、効率を良くしてみましょう。
結果を記録するためのデータコンテナとして、今回はシンプルにリストを採用します。
def fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
fibonacci_numbers = [0] * (n + 1)
fibonacci_numbers[1] = 1
for index in range(2, n + 1):
fibonacci_numbers[index] = fibonacci_numbers[index - 1] + fibonacci_numbers[index - 2]
return fibonacci_numbers[n]
まずは初めに、n=0のときと、n=1のときにはそのまま値を返すようにしています。
if n == 0:
return 0
if n == 1:
return 1
次に、内部に要素数n+1のリストを用意し、0で初期化しています。これは、たとえばn=3であれば、0番目、1番目、2番目、3番目で、合計4個のリストが必要だからです。
fibonacci_numbers = [0] * (n + 1)
さらに、n=1のときの値を1として手動で初期化しています。手前2つの数の和がフィボナッチ数なので、2番目の数を求める際には、0番目だけでなく、1番目の数も必要になるからです。
fibonacci_numbers[1] = 1
そして、ここが大きな違いなのですが、先程までreturn fibonacci(n - 1) + fibonacci(n - 2)としていたところを、リストへの要素のアクセスに置き換えています。
for index in range(2, n + 1):
fibonacci_numbers[index] = fibonacci_numbers[index - 1] + fibonacci_numbers[index - 2]
一瞬似たような処理をしているように見えなくもないですが、fibonacci_number[index - 1]もfibonacci_numbers[index - 2]も、どちらもリストから要素を読み出しているだけなので、再帰呼び出しをするより高速に計算可能です。
この関数であれば、n=50のときのフィボナッチ数もさくっと求められます。
from time import perf_counter
start = perf_counter()
print(fibonacci(50))
end = perf_counter()
print(f"time: {end - start:.5f}s")
12586269025
time: 0.00025s
また、階乗を求める関数も同様に動的計画法を用いて作成可能です。
def factorial(n):
factorial_numbers = [0] * (n + 1)
factorial_numbers[0] = 1
for index in range(1, n + 1):
factorial_numbers[index] = index * factorial_numbers[index - 1]
return factorial_numbers[n]
f3000 = factorial(3000)
なお、桁数が大きすぎるため、表示限界を変更しないと
Exceeds the limit (4300 digits) for integer string conversion; use sys.set_int_max_str_digits() to increase the limit
というエラーを吐きます。
sys.set_int_max_str_digits(10000)
print(f3000)
414935960343785408555686709308661217095111919....(以下省略)
以上のように、計算結果を記録し、再帰処理の部分を呼び出しに変更することで、素早く計算ができるようになりました。
なお、単純に再帰処理の必要時間を短縮したい場合には、functools.cacheの活用も手段の一つです。動的計画法からは外れますので、以下に折りたたんでおきます。(2024/7/23追加)
functools.cacheについて
標準ライブラリに実装されたデコレータの一つです。キャッシュの名前の通り、一度実行した結果を保存してくれます。使い方は簡単で、functools.cacheをデコレートするだけです。
一つ注意点があるとすれば、引数をキーとした辞書を内部に記録することで、結果の保存を行っている点です。そのため、デコレートされる側の関数の引数は辞書のキーに用いることができるもの=hash可能なものでなければなりません。リストなどはNGということですね。
それでは前置きはこのくらいにして、それぞれの実行速度の差を計測してみましょう。
import functools
from time import perf_counter
def fibonacci_without_cache(n):
if n == 0:
return 0
elif n == 1:
return 1
return fibonacci_without_cache(n - 1) + fibonacci_without_cache(n - 2)
@functools.cache
def fibonacci_with_cache(n):
if n == 0:
return 0
elif n == 1:
return 1
return fibonacci_with_cache(n - 1) + fibonacci_with_cache(n - 2)
start = perf_counter()
print(fibonacci_without_cache(40))
end = perf_counter()
print(f'time_delta: {end - start:.3f}')
print('-----------------')
start = perf_counter()
print(fibonacci_with_cache(40))
end = perf_counter()
print(f'time_delta: {end - start:.3f}')
102334155
time_delta: 38.349
-----------------
102334155
time_delta: 0.000
もちろんスペックにはよりますが、露骨に早くなります。引数がハッシュ可能であるという条件を満たせるのであれば、積極的に活用したいところです。
ナップサック問題への適用
今度は少し複雑な例として、ナップサック問題を持ち出してみます。ナップサック問題は割と昔からあるらしい(1940年代くらい?)問題で、「特定の重さと価値を持つアイテムがある。決まった容量のナップサックで価値を最大化すると、その価値はいくつになるか」といったものです。
初めて見ると、何だか小難しく感じられるかもしれませんが、要するに所持重量に制限があるオープンワールドゲームなんかでよく悩むことになるアレです。
武器などの大物は価値が高いが、その分重くて所持重量を圧迫する。一方で、ジャンク品などの小物は軽いが価値は低い。さて、自分はこの目の前のアイテムをそのままにしておくべきか?あるいは、インベントリのアイテムを捨ててでも持ってかえるべきか?のような考え方です。
この問題もフィボナッチ数や階乗のように、動的計画法を用いて解くことができます。まずはコード、次に概要を確認してみましょう。
コードを追いかけてみる
def knapsack_solve(weights, values, capacity):
n = len(weights)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for w in range(1, capacity + 1):
dp[i][w] = dp[i - 1][w]
if weights[i - 1] <= w:
dp[i][w] = max(dp[i][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])
return dp[n][capacity]
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 8
print(knapsack_solve(weights, values, capacity))
結構複雑なコードですね。
まず、ざっくりとした基本方針として、縦がアイテムの個数+1、横がナップサックの容量+1のテーブルを用意して、そこにその時々の一番最適な価値を記録していくというプログラムになっています。
アイテムを1つずつ見ながら、容量が0のときはこう、2のときはこう……という感じですね。結果として二重のループを用いることになります。
それではコードを部分ごとに確認していきましょう。
まず、アイテムの設定がここです。
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
上から重さと価値ですね。アイテムにはそれぞれ重さと価値がありますが、weightsとvaluesはそれぞれ順番で対応しています。たとえばweights[0]である2の重さのアイテムは、values[0]である3の価値を持っています。
その後に来るのがこちら。ナップサックの容量です。
capacity = 8
ここはそのままで、あまり説明することもありませんね。
次は関数を見ていきましょう。関数の1行目で、次の初期化に必要な数を取得しています。
n = len(weights)
weightsの要素数、つまり4という値がnには代入されています。これはそのままアイテム数のことです。そのため、
n = len(values)
でも同じ動作になります。
次の行は、記録用に必要なテーブルの作成です。
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
内包表記を用いて、リスト内リストを作成していますね。ただ、少し分かりづらいので、具体的な数と入れ替えてみましょう。
dp = [[0] * (8 + 1) for _ in range(4 + 1)]
まだ見辛いと感じる場合は、普通のfor文に書き換えるのも手です。
dp = []
for _ in range(4 + 1):
dp.append([0] * (8 + 1))
どちらの場合でも、このようなリストができます。
[[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0]]
行はアイテムなし、アイテム1, アイテム2, アイテム3, アイテム4に対応しています。また列は、容量0, 1, 2…にそれぞれ対応しています。表に直すと、以下のような感じです。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
さて、ここからは以下のforループを回しながら価値を最大化していくわけですが、少しわかりづらい流れになっています。
そのため、いったん変更されない1行目と1列目以外を空っぽにして、値がどのように増えていくかをループと共に追いかけていきましょう。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0
2 0
3 0
4 0
まずは、nを置き換えたループのコードが以下のようになります。
for i in range(1, 4 + 1):
for w in range(1, 8 + 1):
dp[i][w] = dp[i - 1][w]
if weights[i - 1] <= w:
dp[i][w] = max(dp[i][w], values[i - 1] + dp[i - 1][w - weights[i - 1]])
いったんi, wの変化だけ追いかけていくと、以下のようなコードになります。
for i in range(1, 4 + 1):
for w in range(1, 8 + 1):
print(f"i: {i}, w: {w}")
i: 1, w: 1
i: 1, w: 2
i: 1, w: 3
i: 1, w: 4
i: 1, w: 5
i: 1, w: 6
i: 1, w: 7
i: 1, w: 8
i: 2, w: 1
i: 2, w: 2
i: 2, w: 3
i: 2, w: 4
i: 2, w: 5
i: 2, w: 6
i: 2, w: 7
i: 2, w: 8
i: 3, w: 1
i: 3, w: 2
i: 3, w: 3
i: 3, w: 4
i: 3, w: 5
i: 3, w: 6
i: 3, w: 7
i: 3, w: 8
i: 4, w: 1
i: 4, w: 2
i: 4, w: 3
i: 4, w: 4
i: 4, w: 5
i: 4, w: 6
i: 4, w: 7
i: 4, w: 8
0行を除き、1行1列, 1行2列, 1行3列と1行目をチェック。これが終わり次第、2行1列、2行2列と2行目をチェック……という流れです。そのため先程の表は、全体としては上から下、行ごとだと左から右と、ちょうど横書きの文章を読む時の順番で更新されていくことになります。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 → → → → → → → ↙
2 0 → → ...
3
4
それでは、$(i, w) = (1, 1)$から順番に追いかけていきましょう。数字を代入したコードは以下のようになります。
dp[1][1] = dp[0][1]
if weights[0] <= 1:
dp[1][1] = max(dp[1][1], values[0] + dp[0][w - weights[0]])
まずはコードの1行目。ここでは、0行1列の値を1行1列に代入しています。
dp[1][1] = dp[0][1]
値が上からスライドしてきている形ですね。チェックしているアイテムを追加しないときの価値を、仮の最適な価値として登録している状態になります。
表は以下のようになります。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0←new!
2 0
3 0
4 0
次はコードの2行目です。
if weights[0] <= 1:
ここではweights[0]、つまり初めのアイテムが、今チェックしている容量である1より小さいかを調べています。
話はシンプルで、詰めたいアイテムが今の容量より小さいか、つまりそもそも詰めることが可能かどうかをチェックしています。詰めたいアイテムが今の容量より大きい場合、つまりアイテムを詰めることが出来なかった場合には、先程dp[1][1] = dp[0][0]で行った仮設定が、自動的に最適になるため、詰めたあとのチェックは不要です。
weights[0]は2であるため、2<=1は成立せず、今回のif文の中身はスキップされます。そのため、表も先程と変わることはありません。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0←not change
2 0
3 0
4 0
さて、次は$(i, w) = (1, 2)$のとき、すなわち同じアイテム1が容量2のときは入りうるかどうかというチェックです。
dp[1][2] = dp[0][2]
if weights[0] <= 2:
dp[1][2] = max(dp[1][2], values[0] + dp[0][2 - weights[0]])
まずは先程と同じく、上の行の数字をスライドさせます。アイテムを入れないのが最適だという仮定ですね。
dp[1][2] = dp[0][2]
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 0←new!
2 0
3 0
4 0
次に重さのチェックです。
if weights[0] <= 2:
先程は通らなかったチェックですが、今回は通ります。weights[0]は2なので、2<=2はTrueです。
そして、この後さらなるチェックが入ります。
dp[1][2] = max(dp[1][2], values[0] + dp[0][2 - weights[0]])
dp[1][2]は今チェックしている箇所なので、現在の値です。それと、values[0] + dp[0][2 - weights[0]]を比較して、大きい方を採用しています。
まずvalues[0]ですが、これはシンプルに今入れようとしているアイテムの価値、つまり3です。
それと、多分ここが一番ややこしいのですが、dp[0][2 - weights[0]]、すなわちdp[0][0]が出てきます。これは、前のアイテムをチェックした1行上の、さらに2つ左の値を呼び出しています。下の表のビックリマークのところです。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0←!0 0 0 0 0 0 0 0
1 0 0 0←now
2 0
3 0
4 0
この場所を呼び出したのは、容量が今よりアイテムの重さの分だけ少なかったときの最も高かった価値が記録してあるからです。
そもそも、今のアイテムを入れたときの価値は、「追加したアイテムの価値+今のナップサックの価値」ではありません。これだと容量が4になってしまいます。
今はあくまで容量が2のときの話をしていますので、正しくは「追加したアイテムの価値+容量が2-2=0だったときの最も高かった価値」です。このうち後者を呼び出しているのがビックリマークの部分です。
初めに持ち出したゲームの例でたとえるならば、いったんアイテムを戻して、容量を空けた上で価値を考えている感じですね。
そして具体的な動作ですが、1行上の2列手前のビックリマーク部は0なので、結局、maxを用いたコードの部分を計算すると、
dp[1][2] = max(dp[1][2], values[0] + dp[0][0])
から更に、
dp[1][2] = max(0, 3 + 0)
となり、当然3の方が大きいので、dp[1][2]は3と決定されます。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3←update
2 0
3 0
4 0
もう一つ追いかけてみましょう。次は$(i, w)=(1, 3)$のとき、すなわちアイテム1が容量3のときの最適解には入りうるかどうかというチェックです。
i, wに関連する計算だけすませたコードは以下のようになります。
dp[1][3] = dp[0][3]
if weights[0] <= 3:
dp[1][3] = max(dp[1][3], values[0] + dp[0][3 - weights[0]])
とりあえず上の価値を仮で持ってきて、
dp[1][3] = dp[0][3]
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 0←new!
2 0
3 0
4 0
ifのチェックが通ることを確認し、
# if weights[0] <= 3:
if 2 <= 3:
比較を行います。
dp[1][3] = max(dp[1][3], values[0] + dp[0][3 - weights[0]])
dp[1][3]は、先程仮に読み込んだ0, values[0]は3, weights[0]は2なので、そこまで含めて計算すると、
dp[1][3] = max(0, 3 + dp[0][1])
のようになります。一つ手前の最適な状態として呼び出されるのは、以下のビックリマークの部分です。3-2=1で、容量が1の部分ですね。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0←!0 0 0 0 0 0 0
1 0 0 3 0
2 0
3 0
4 0
結局maxを含む行は以下のようになり、値が更新されます。
dp[1][3] = max(0, 3 + 0)
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3<-update!
2 0
3 0
4 0
それで、ここまで読んでいただいてわかったと思うのですが、アイテム1をチェックしている間は常に価値が3と更新され続けます。比較の基準である0行目が全て0なので、当然といえば当然ですね。
そこで、1行目の残りは全て3で埋めてしまった上で、2行目、つまりアイテム2のチェックに入りたいと思います。アイテム2は重さが3, 価値が4のアイテムで、チェックすべき行は以下の→の部分になります。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 → → → ...
3 0
4 0
以降のコードでは、i=2だとして扱っていきます。
# i = 2
for w in range(1, capacity + 1):
dp[2][w] = dp[1][w]
if weights[1] <= w:
dp[2][w] = max(dp[2][w], values[1] + dp[1][w - weights[2]])
さて、まずはw=1の時のチェックです。
# w = 1
dp[2][1] = dp[1][1]
if weights[1] <= 1:
dp[2][1] = max(dp[2][1], values[1] + dp[1][1 - weights[2]])
まずは仮の最適値として1行上の値を呼び出します。
dp[2][1] = dp[1][1]
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0←new!
3 0
4 0
次にifのチェックですが、weights[1]=なので、これは通りません。そのため、ここの場所は値が更新されることなくw=1のループは終わります。
# if weights[1] <= 1:
if 2 <= 1:
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0←decided!
3 0
4 0
次はw=2の時のループ……といいたいところですが、ここも全く同じ動作になるので飛ばします。アイテムの重さが3で容量が2なので、上の行の3を読みこんだ後は、更新する余地はありません。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3←skip
3 0
4 0
次はw=3のときです。ここはちょっとだけ面白くなります。ついでにweights[2]=3まで埋めた上で確認してみましょう。
# w = 3, weights[2] = 3
dp[2][3] = dp[1][3]
if weights[1] <= 3:
dp[2][3] = max(dp[2][3], values[1] + dp[1][0])
まずは、以下のコードで上の値を仮に呼び出します。
dp[2][3] = dp[1][3]
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 3←new!
3 0
4 0
次に、ifのチェックが通り、
# 3 <= 3
if weights[1] <= 3:
maxを含むさらなる判定に進みます。ついでに価値も代入しておきましょう。
dp[2][3] = max(dp[2][3], 4 + dp[1][0])
ここで、dp[2][3]は3, dp[1][0]は0です。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0←!0 3 3 3 3 3 3 3
2 0 0 3 3←now
3 0
4 0
そのため、maxを含む部分は以下のようになります。
dp[2][3] = max(3, 4 + 0)
4の方が大きいので値が更新されます。状態を巻き戻して、つまり3の価値を持つアイテムを捨てて入れ替えた形ですね。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 4←update!
3 0
4 0
次は大きさがナップサックの容量が4のときになりますが、こちらは同じ動作になるので省略します。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 4 4←same value
3 0
4 0
次はwが5のときです。こちらは動作が変わるのでチェックしましょう。
まず例のごとく、上の値を仮の値として読み込みます。
dp[2][5] = dp[2 - 1][5]
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 4 4 3←new!
3 0
4 0
次にifのチェックはしっかりと通るため、maxを使ったさらなる判定に入ります。
# 3 <= 5
if weights[2 - 1] <= w:
dp[2][5] = max(dp[2][5], values[2 - 1] + dp[2 - 1][5 - weights[2 - 1]])
こちらに値を代入すると、以下のようになります。
dp[2][5] = max(3, 4 + 3)
先程と同じく、一段上の3つ左、つまり今のアイテムを含まない状態での最も高い価値を読み込んでいます。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3←!3 3 3 3 3 3
2 0 0 3 4 4 3
3 0
4 0
当然、7の方が大きいので、値が更新されます。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 4 4 7←update!
3 0
4 0
この調子でプログラムを進めていくと、最終的には以下のような表になり、最大の価値は10であると求めることが可能です。
容量 0 1 2 3 4 5 6 7 8
アイテム
0 0 0 0 0 0 0 0 0 0
1 0 0 3 3 3 3 3 3 3
2 0 0 3 4 4 7 7 7 7
3 0 0 4 5 5 7 8 9 9
4 0 0 3 4 5 7 8 9 10
コードを改造してみる
以上で動的計画法の話は終わりなのですが、このコードのままですと、最大の価値がわかってもその詰め方までははっきりとしません。また、アイテムが異なるリストに分割されて、順番だけで対応しているのも少し分かりづらさを感じます。
そこで、
- アイテムの情報をひとまとめにして、扱いやすくする
- アイテムの情報に価値を重量で割った割合を追加し、単品での価値を確認できるようにする
- バックトラックを行うようにして、どのアイテムが追加されたのか確認できるようにする
- 選ばれたアイテム群に対し、単純な割合は高いアイテムがどの程度選ばれているのかを確認できるようにする
という変更を行ったコードが以下になります。
from dataclasses import dataclass
from random import randint
MIN_CAPACITY = 100
MAX_CAPACITY = 500
MIN_VALUE = 5
MAX_VALUE = 200
MIN_WEIGHT = 50
MAX_WEIGHT = 100
@dataclass
class Item:
name: str
value: int
weight: int
def __post_init__(self):
self.value_to_weight_ratio = self.value / self.weight
def __str__(self):
return f"name: {self.name}, value: {self.value}, weight: {self.weight}, value_to_weight_ratio: {self.value_to_weight_ratio:.3f}"
def __eq__(self, other):
if not isinstance(other, Item):
return False
return (self.name == other.name) and (self.value == other.value) and (self.weight == other.weight)
def __hash__(self):
return hash((self.name, self.value, self.weight))
def knapsack(items: list[Item], capacity: int) -> tuple[int, list[Item]]:
n = len(items)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
for w in range(1, capacity + 1):
dp[i][w] = dp[i - 1][w]
if items[i - 1].weight <= w:
dp[i][w] = max(dp[i][w], items[i - 1].value + dp[i - 1][w - items[i - 1].weight])
w = capacity
selected_items = []
for i in range(n, 0, -1):
if dp[i][w] != dp[i - 1][w]:
selected_items.append(items[i - 1])
w -= items[i - 1].weight
return dp[n][capacity], selected_items
items = [Item(f"Item{i}", value=randint(MIN_VALUE, MAX_VALUE), weight=randint(MIN_WEIGHT, MAX_WEIGHT)) for i in range(10)]
capacity = randint(MIN_CAPACITY, MAX_CAPACITY)
print(f"capacity: {capacity}")
maximum_value, selected_items = knapsack(items, capacity)
print(f"Maximum value: {maximum_value}")
selected_item_length = len(selected_items)
print("-----------------------------")
print("sorted selected items by ratio")
sorted_selected_items = sorted(selected_items, key=lambda item: item.value_to_weight_ratio, reverse=True)
for item in selected_items:
print(item)
print("-----------------------------")
print(f"{selected_item_length} items sorted by ratio")
sorted_items = sorted(items, key=lambda item: item.value_to_weight_ratio, reverse=True)[: selected_item_length]
for item in sorted_items:
print(item)
print("-----------------------------")
print("common items")
if (common_items := set(sorted_selected_items) & set(sorted_items)):
for item in common_items:
print(item)
else:
print("nothing!")
capacity: 116
Maximum value: 194
-----------------------------
sorted selected items by ratio
name: Item9, value: 108, weight: 55, value_to_weight_ratio: 1.964
name: Item8, value: 86, weight: 55, value_to_weight_ratio: 1.564
-----------------------------
2 items sorted by ratio
name: Item2, value: 178, weight: 66, value_to_weight_ratio: 2.697
name: Item1, value: 170, weight: 65, value_to_weight_ratio: 2.615
-----------------------------
common items
nothing!
価値と重さ、そしてナップサックの容量次第では、単純な重さあたりの価値が高いものが選ばれるわけではないという面白い結果が出ます。
最後に、変わった部分を軽く確認しておきましょう。
MIN_CAPACITY = 100
MAX_CAPACITY = 500
MIN_VALUE = 5
MAX_VALUE = 200
MIN_WEIGHT = 50
MAX_WEIGHT = 100
ナップサックの容量と、価値・重さをランダムに決めるときの最大値、最小値です。適当に弄ると面白いです。
@dataclass
class Item:
name: str
value: int
weight: int
def __post_init__(self):
self.value_to_weight_ratio = self.value / self.weight
def __str__(self):
return f"name: {self.name}, value: {self.value}, weight: {self.weight}, value_to_weight_ratio: {self.value_to_weight_ratio:.3f}"
def __eq__(self, other):
if not isinstance(other, Item):
return False
return (self.name == other.name) and (self.value == other.value) and (self.weight == other.weight)
def __hash__(self):
return hash((self.name, self.value, self.weight))
ハッシュ処理用と、表示用のメソッドを整えています。それと、__post_init__を使って、init後に重量あたりの価値を計算してインスタンス属性に格納しています。ちょっとした処理に便利ですね。
ハッシュ処理は主に最後のfrozenset型への変換のために用いています。初めはdataclass(frozen=True)を用いようと思ったのですが、postの処理を受け入れないようなのでスルーしています。
なお、set型とfrozenset型については、以下の記事にまとめていますので、よろしければご確認下さい。
Qiita:【Python】”とりあえずリスト病”の治療1:set型, frozenset型について
w = capacity
selected_items = []
for i in range(n, 0, -1):
if dp[i][w] != dp[i - 1][w]:
selected_items.append(items[i - 1])
w -= items[i - 1].weight
バックトラック用のコードです。仕組みとしてはとてもシンプルで、初めにアイテム格納用のリストを用意しています。そこから、テーブルを逆に辿っていっています。仮の値が常に1行上から流用されているのを使い、値が異なっている=その行で取り扱ったアイテムが追加されている、という流れで確認しています。
items = [Item(f"Item{i}", value=randint(MIN_VALUE, MAX_VALUE), weight=randint(MIN_WEIGHT, MAX_WEIGHT)) for i in range(10)]
capacity = randint(MIN_CAPACITY, MAX_CAPACITY)
print(f"capacity: {capacity}")
maximum_value, selected_items = knapsack(items, capacity)
print(f"Maximum value: {maximum_value}")
selected_item_length = len(selected_items)
print("-----------------------------")
print("sorted selected items by ratio")
sorted_selected_items = sorted(selected_items, key=lambda item: item.value_to_weight_ratio, reverse=True)
for item in selected_items:
print(item)
print("-----------------------------")
print(f"{selected_item_length} items sorted by ratio")
sorted_items = sorted(items, key=lambda item: item.value_to_weight_ratio, reverse=True)[: selected_item_length]
for item in sorted_items:
print(item)
print("-----------------------------")
print("common items")
if (common_items := frozenset(sorted_selected_items) & frozenset(sorted_items)):
for item in common_items:
print(item)
else:
print("nothing!")
長くてごちゃついている割には余り面白くない部分です。返ってきた値の確認をしつつ、選ばれたアイテムと同じ数だけ、重量あたりの価値が高いアイテムを取り出した上で、どれだけ共通のアイテムがあるのかを確認できるようにしました。
あとがき
これまで余りアルゴリズムに触れる機会がなく、理解にかなり苦戦しました。今回の記事も、備忘録の側面が強いです。何かしら補足・指摘があればコメント欄にあれば、宜しくお願い致します。