誤解の多い中心極限定理の超概要

統計初学者に取って中心極限定理は理解しにくく

一定数以上のデータを集めると、その分布は必ず正規分布になる

という誤った解釈をされている方が結構多いようです。

この文書では、統計を学び始めた方を想定し、中心極限定理の超概要について説明します。

説明は以下の順序で行います。

1. 実世界から取ってきたデータの分布は様々であること
2. 中心極限定理の超概要を具体例を使って説明

実世界から取ってきたデータの分布は様々

実世界から取ってきたデータは様々な分布になります。一定数以上のデータを取って来ると必ず正規分布になるということはありません。

実は至極当たり前のことなのですが、言葉だけだとイメージが湧かず理解しにくいと思うので、筆者が考えた具体例を使って説明してみます。

成績一覧

学校の生徒1000人の成績評価（５段回）の一覧です。

4が多く５が少ないのは、そういう成績配分ルールにしてるからです。

売り上げ 

お客様一人当たりの売り上げ金額の一覧です

5000円に集中しているのは、5000円の目玉商品があったからです。

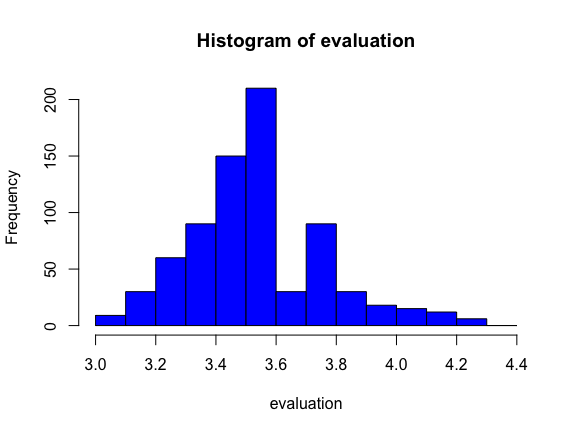
製品評価

製品評価サイトの様々な製品評価の一覧です。評価はサイト運営者が独自のロジックで作成しています。

3.6に固まってるのはそういう評価ロジックにしてるからです。

• 3.6に到達した時点で一定期間その点数でホールド
• 一定期間安定して評価が継続する場合のみ3.6以上の得点を表示する

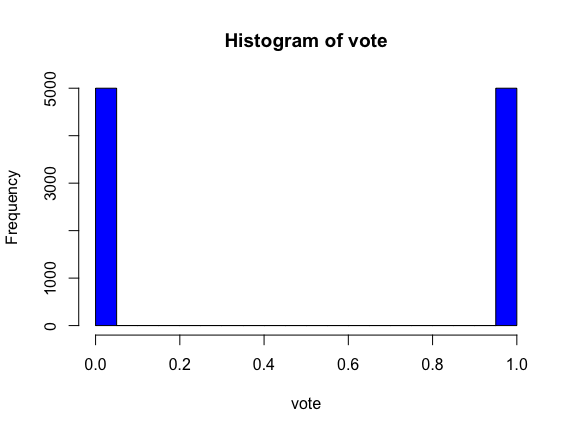
投票結果

法案の可否を問う投票の結果です

賛成と反対が半々なのは、法案への賛否両論だったからです。

このように現実世界のデータを持ってきた場合、その分布は様々です。

一定数以上のデータを集めると、その分布は必ず正規分布になるという理解は誤りです。

中心極限定理超概要

ここからは中心極限定理の超概要を述べてみます。

中心極限定理
同一の母集団からランダムに収集したサンプルの平均値（もしくは合計値）の分布はサンプルサイズが大きくなるにつれて正規分布に収束する。

中心極限定理を具体例で説明

さっき例にあげた投票を使って中心極限定理を説明してみます

投票結果 　賛成 : 5000人  反対 : 5000人

この投票、賛成の人は黒玉 を、反対の人は白玉を投票箱に入れるという形式で行われたとしましょう。

今その投票箱が目の前にあるとして、以下の作業を行ってデータを収集してください。

1. この投票箱をよく振って、30個の玉を取り出して下さい

1. 黒玉(賛成投票)の個数を数えてください
2. 数え終わったらまた投票箱に戻して、よく振ってください

まずは3回やってデータを収集してみました、こちらがその結果です。

1回目 : 15個
2回目 : 17個
3回目 : 13個

投票箱をおみくじみたいに振ってから取り出してるので、当然毎回黒玉の数は違いますね。

この作業を何回もやると黒玉の数がどんな分布をするか見てみましょう。

この後の説明を簡単にするため取り出した黒玉の割合を算出して、そっちの数字を使うことにします。

• 1回目 : 50% (15個/30個)
• 2回目 : 57% (17個/30個)
• 3回目 : 43% (13個/30個)

この作業を10000回やって、結果を表にしてみました。

分布がなだらかな曲線になってますね。これが正規分布です。（正確には正規分布に近い分布）

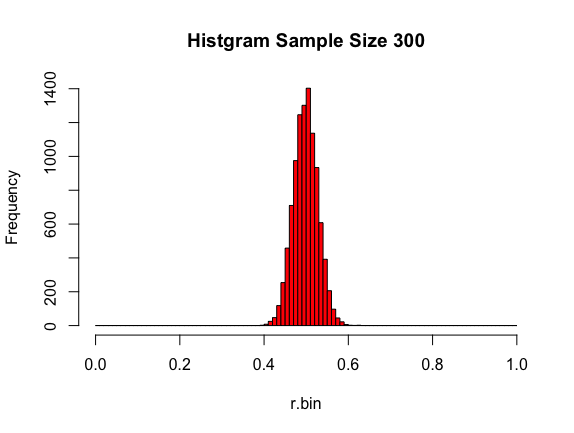
今度はサンプルサイズを300にしてやってみましょう

これも正規分布になってますね。30の時より幅が狭くなってます。

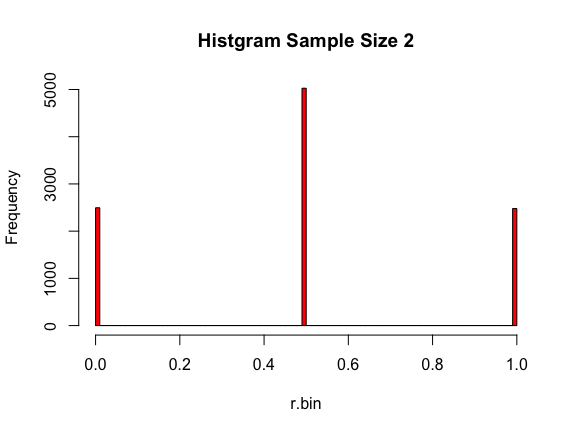
今度は逆にサンプルサイズを少なくして２にしてみましょう。

これは正規分布って感じじゃないですね。

サンプル数が一定数以上になると、母集団の平均(この場合は0.5)を中心に左右対象のなだらかな下り坂になる正規分布と呼ばれる分布に近いものになります。
サンプル数を増やすと平均の周りへの密集度が増しています。
どのくらいのサンプル数で正規分布っぽくなって来るかは母集団の形状により違ってきます。

これが中心極限定理と言われるものです

もう一度、中心極限定理の定義と、今回やった作業を振り返ってみましょう。

中心極限定理の定義

同一の母集団からランダムに収集したサンプルの平均値（もしくは合計値）はサンプルサイズが大きくなるにつれて正規分布に収束する。

今回やった作業

同一の母集団から: 同じ投票箱から取り出してます
ランダムに収集: 投票箱をよく振ってから取り出してます
サンプルの平均値（もしくは合計値）: 黒玉の数を合計
サンプルサイズが大きくなるにつれて: 今回のサンプルサイズは30個
正規分布に収束する: 30個のサンプルサイズで正規分に近い形になっています

今回は投票結果という母集団からデータをランダムに取ってきましたが、おおよそどんな形の分布の母集団でも、一定数以上のサンプルサイズを持ってきて平均するという作業を繰り返すとそれは正規分布になります。

中心極限定理の何が嬉しいのか

統計的な処理を行う際には、この特性が活用されています。

例えば、今回の例では投票箱の中身(賛成:5000,反対:5000)を知ってましたが、これが実際の選挙で全体の投票結果は分からないが、出口調査とかで入手したランダムサンプリングデータを持っているとしましょう。
中心極限定理によるとサンプルの平均は母集団の平均を中心とした正規分布に従い、その分散はサンプル数が大きくなると小さくなるので、全体のデータがなくても、おおよそこのくらいの得票率だろうと推測ができる訳です。

その他色々な活用がされていますが、それはまたの機会に。