本記事は、AI道場「Kaggle」への道 by 日経 xTECH ビジネスAI① Advent Calendar 2019のアドベントカレンダー 9日目の記事です。
Permutation ImportanceがScikit-Learnのversion0.22より導入されました。この手法はKaggleでも使われており1 、特徴選択に有用な方法です。本記事ではこのPermutation Importanceの解説と、LightGBMで5-foldでCVしながら使ってみた例を紹介します。コードの全文はKaggle Kernelとして登録してありますので、コードだけサクっとみたい方はこちらをどうぞ。
1. Permutation Importanceとは
Permutation Importanceとは、機械学習モデルの特徴の有用性を測る手法の1つです。よく使われる手法にはFeature Importance(LightGBMならこれ)があり、学習時の決定木のノードにおける分割が特徴量ごとにどのくらいうまくいっているかを定量化して表していました。本記事で紹介するPermutation Importanceは学習時ではなく、学習済みモデルを用いて各特徴量の効果を計測できる方法です。学習済みモデルを用いるため、検証データ(Validation data)にも適用でき、汎化性能の観点からも各特徴量の良さを計測でき、また木系のモデル以外でも利用できるという利点があります。
2. Permutation Importanceの手順と仕組み
2-1. まずは通常の検証で精度を計測
事前に訓練データでモデルは学習済みとします。検証データを用いてモデルを評価する際は、検証データを学習済みモデルにインプットし、予測結果(y_pred)を算出して、正解データ(Ground Truth)と指定の評価指標で評価(例えばRMSEやAUCなど)し、モデルの良さを測ります。Permutation Importanceはこの検証データの指標評価の値を元に各特徴量の良さを計測するため、最初にベースとなる通常状態の精度を測ります。
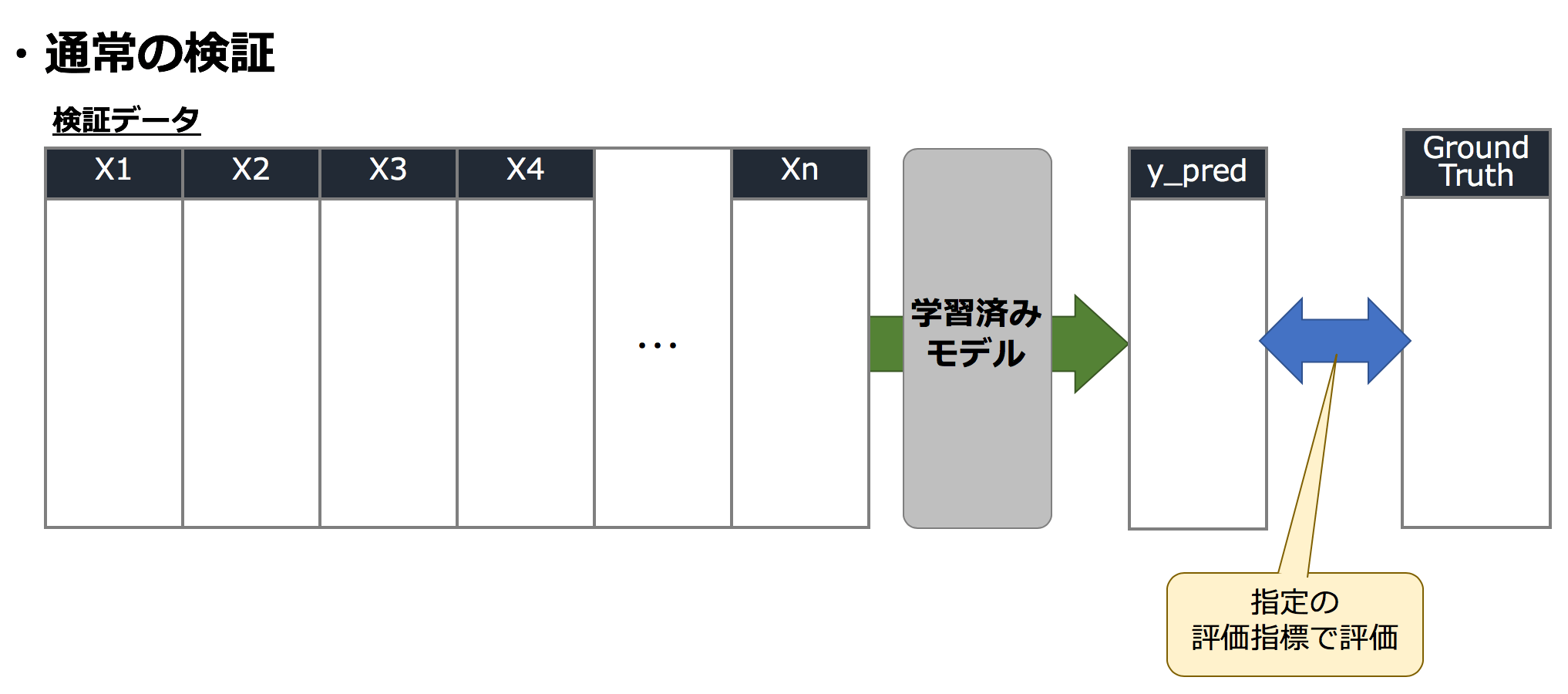
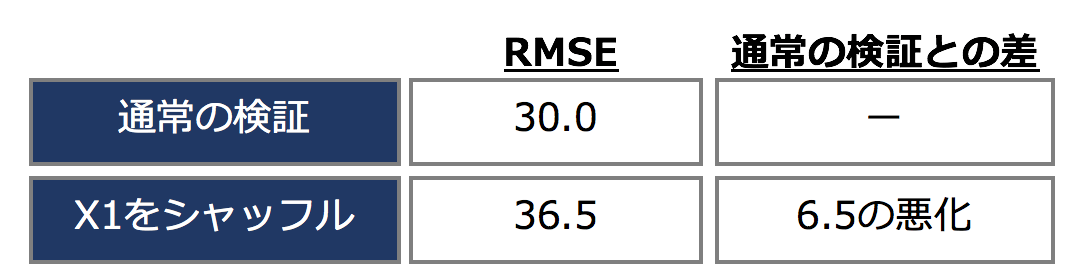
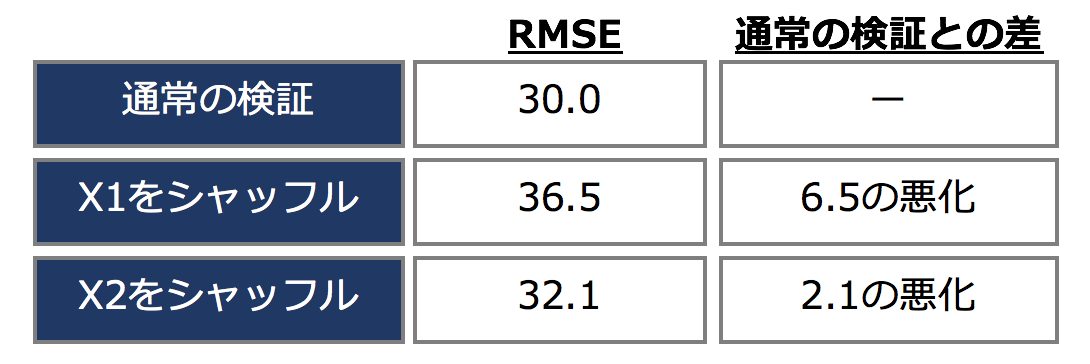
例えばこのとき、評価指標がRMSEで、通常の検証を行い測った結果が RMSE=30.0 であったとします。

2-2. Permutation Importanceを計測
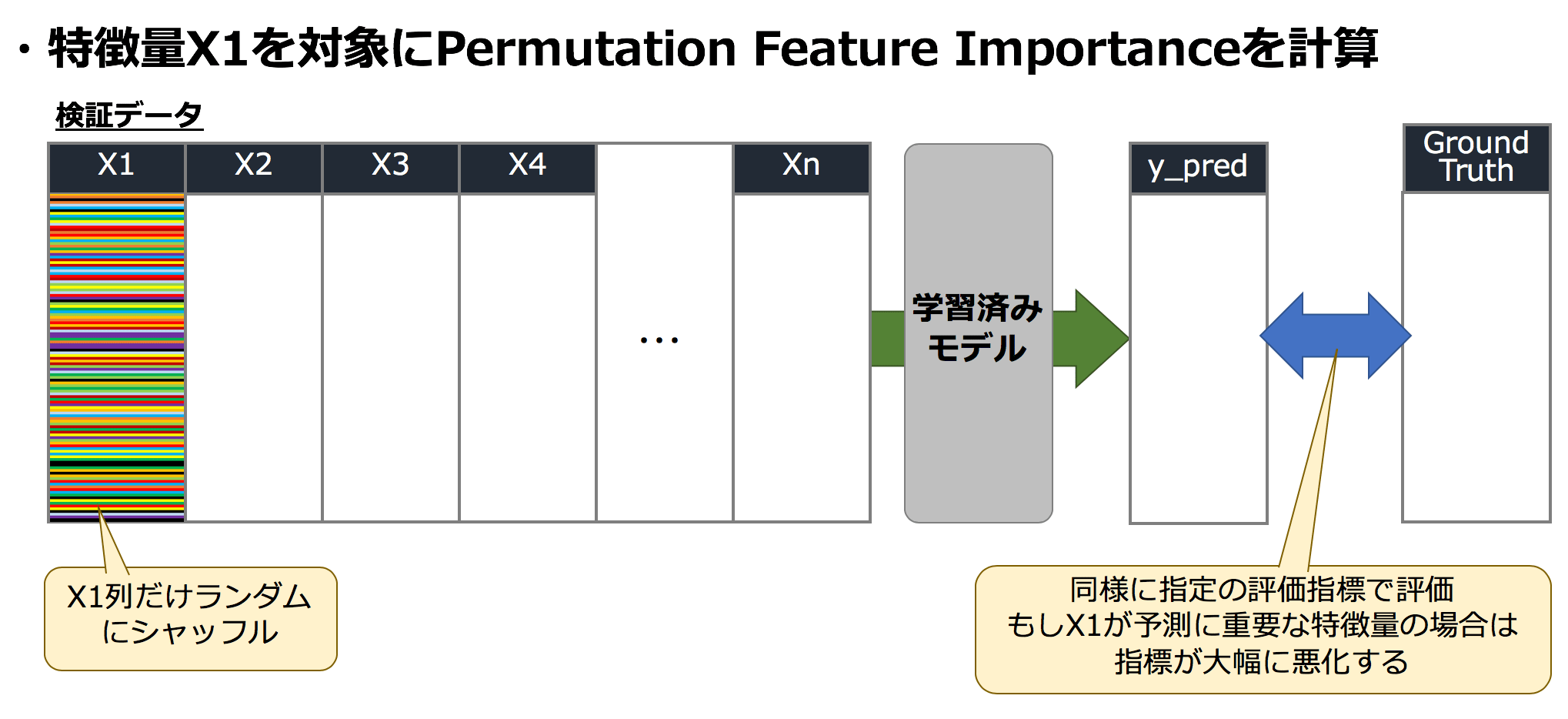
ここからが本番、Permutation Importanceを計測します。いま、与えられている学習用データは X1, …, Xn のn個の特徴量から構成されているとします。まず最初にX1を選びます。ここで、X1をランダムにシャッフルしてしまいます。これを検証データとして学習済みデータにインプットして同様に予測結果(y_pred)を算出して、正解データ(Ground Truth)で評価します。
なぜこのようなことをするかというと、もしX1が非常に有用な特徴であったとすると、ランダムにシャッフルされたX1を含む検証データでは、先ほどの通常の検証と比べ、精度がかなり悪化しているはずである、という仮説に基づくのです。
逆に、X1がこの問題に対してほとんど効果を持っていないとすると、X1をランダムにシャッフルしても精度はほとんど変わらないことが期待されます。
X1のシャッフル
このとき、RMSEが30.0から36.5に変化したとすると、6.5ポイントの悪化がみられ、この量がX1の効果と考えられます。
X2のシャッフル
同様にX2に対しても、X2のみをシャッフルした検証データを学習済みモデルにインプット、精度を測定します。
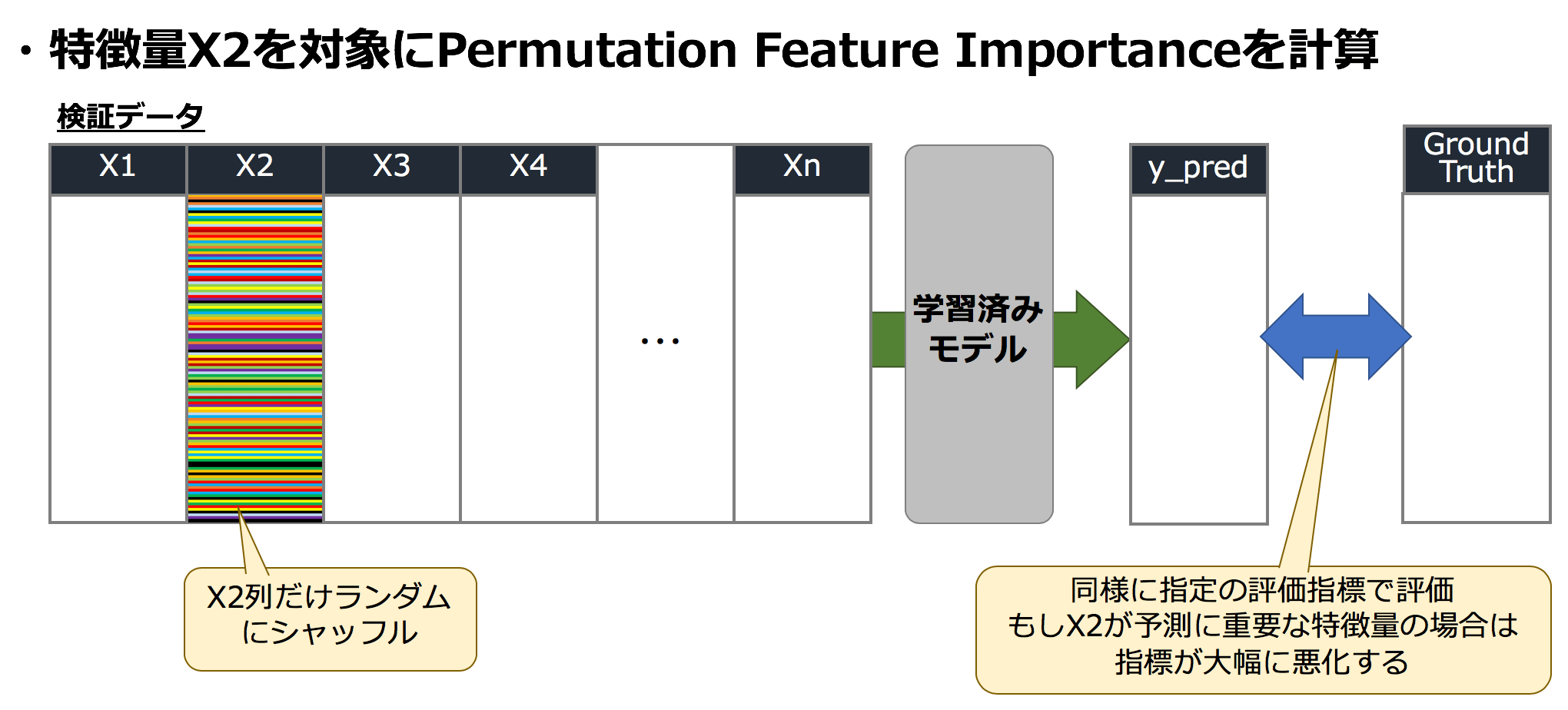
このとき、RMSEが30.0から31.1に変化したとすると、2.1ポイントの悪化がみられ、この量がX2の効果と考えられます。
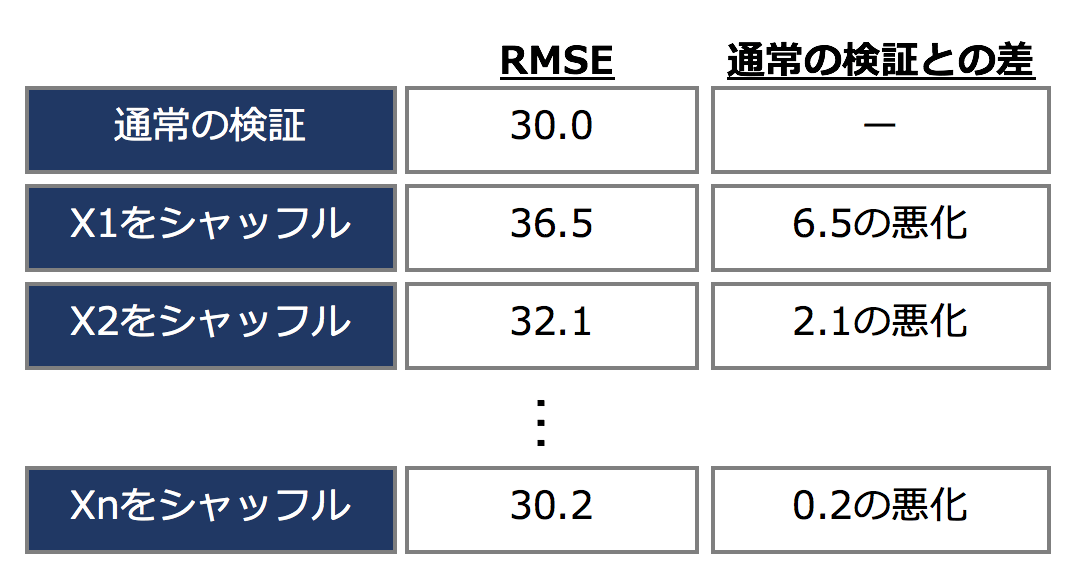
各特徴量1つずつシャッフルして精度差を記録
上記のオペレーションを1つずつ全ての特徴量に対して行います。結果、下記のような表が出来上がり、各特徴に対して通常と検証との差がわかります。差が大きい方が有効な特徴量、差が小さい方が効果が小さい特徴量と考えることができます。この場合はX1が一番差が大きいので有用な特徴ですね。Xnはほとんど差に変化がないので、あまり効いてない特徴と言えそうです。
3. 実際にPermutation Importanceを計測してみる
3-1. 利用データ : Boston house prices dataset
今回はScikit-Learnに付属のBoston house prices datasetを利用します。データの概要は下記の通りです。住居価格の予測なので回帰の問題ですね。
ターゲット
住居の価格
説明変数
| 名前 | 説明 |
|---|---|
| CRIM | per capita crime rate by town |
| ZN | proportion of residential land zoned for lots over 25,000 sq.ft. |
| INDUS | proportion of non-retail business acres per town |
| CHAS | Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) |
| NOX | nitric oxides concentration (parts per 10 million) |
| RM | average number of rooms per dwelling |
| AGE | proportion of owner-occupied units built prior to 1940 |
| DIS | weighted distances to five Boston employment centres |
| RAD | index of accessibility to radial highways |
| TAX | full-value property-tax rate per $10,000 |
| PTRATIO | pupil-teacher ratio by town |
| B | 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town |
| LSTAT | % lower status of the population |
| MEDV | Median value of owner-occupied homes in $1000's |
データイメージ
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00632 | 18 | 2.31 | 0 | 0.538 | 6.575 | 65.2 | 4.090 | 1 | 296 | 15.3 | 396.9 | 4.98 |
| 0.02731 | 0 | 7.07 | 0 | 0.469 | 6.421 | 78.9 | 4.967 | 2 | 242 | 17.8 | 396.9 | 9.14 |
| 0.02729 | 0 | 7.07 | 0 | 0.469 | 7.185 | 61.1 | 4.967 | 2 | 242 | 17.8 | 392.8 | 4.03 |
| 0.03237 | 0 | 2.18 | 0 | 0.458 | 6.998 | 45.8 | 6.062 | 3 | 222 | 18.7 | 394.6 | 2.94 |
| 0.06905 | 0 | 2.18 | 0 | 0.458 | 7.147 | 54.2 | 6.062 | 3 | 222 | 18.7 | 396.9 | 5.33 |
3-2. 計算する
Permutation Importanceはsklearn.inspectionにあるので、インポートします。
from sklearn.inspection import permutation_importance
通常の検証との差をどのように測るかを指定できます。今回はRMSEで測るので、下記のように準備しておきます。
from sklearn.metrics import mean_squared_error, make_scorer
def rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true, y_pred))
mse_scorer = make_scorer(rmse)
次に5-foldでCVの検証をします。Scikit-Learnに準じたI/Fでモデルを作ることでpermutation_importance関数が利用できるので、LightGBMのsklearn wrapperであるlgb.LGBMRegressorを使用します。下記の5-foldループでは、通常のFeature ImportanceとPermutation Importanceの両方を算出しています。seedを変えて各特徴量ごとに複数回shuffleしてばらつきを標準偏差として計算することができ、n_repeatsで指定できます。今回は10回を指定しています。
FOLD_NUM = 5
fold_seed = 71
folds = KFold(n_splits=FOLD_NUM, shuffle=True, random_state=fold_seed)
fold_iter = folds.split(X, y=y)
oof_preds = np.zeros(X.shape[0])
y_preds = np.zeros((FOLD_NUM, X_test.shape[0]))
models = []
importance_list = []
perm_imp_list = []
fold_label = np.zeros(X.shape[0])
for n_fold, (trn_idx, val_idx) in enumerate(fold_iter):
print(f"========= fold:{n_fold} =========")
X_train, X_valid = X.iloc[trn_idx], X.iloc[val_idx]
y_train, y_valid = y[trn_idx], y[val_idx]
params_fit = {'X': X_train,
'y': y_train,
'eval_set': (X_valid, y_valid),
'early_stopping_rounds': 5,
'verbose': False,
'eval_metric': 'l2',
}
model = lgb.LGBMRegressor(objective="regression", n_estimators=100, importance_type="gain", random_state=123)
gbm = model.fit(**params_fit, callbacks=callbacks)
models += [model]
fold_label[val_idx] = n_fold
oof_preds[val_idx] = model.predict(X_valid, model.best_iteration_)
# Feature importance
importance_df = pd.DataFrame({"gain":model.feature_importances_}, index=X.columns).sort_values("gain", ascending=False)
importance_list += [importance_df]
print("[Importance]")
display(importance_df)
# run permutation importance
result = permutation_importance(model, X_train, y_train, scoring=mse_scorer, n_repeats=10, n_jobs=-1, random_state=71)
perm_imp_df = pd.DataFrame({"importances_mean":result["importances_mean"], "importances_std":result["importances_std"]}, index=X.columns)
perm_imp_list += [perm_imp_df]
print("[Permutation feature Importance]")
display(perm_imp_df)
perm_imp_df.sort_values("importances_mean", ascending=False).importances_mean.plot.barh()
plt.show()
1つ目のfoldのRMSEは rmse score = 4.98958でした。
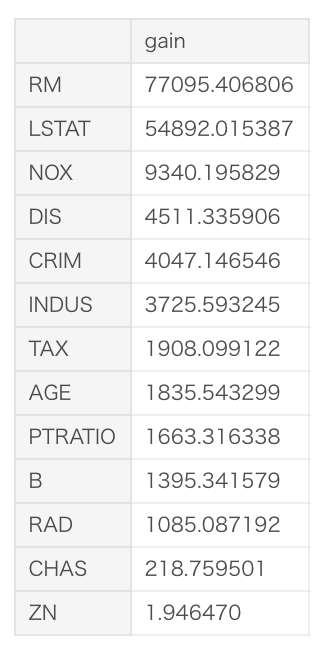
また、1つ目のfoldの通常の重要度、Feature Importanceを表示するとこのようになります。
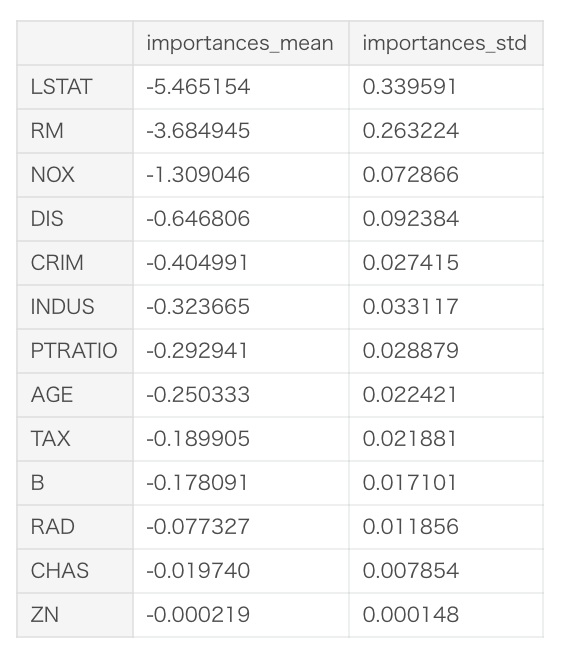
次に、やはり1つ目のfoldのPermutation Importanceを表示すると下記になります。10回seedを変えて繰り返しているので、その平均と標準偏差を表示しています。importances_meanをみると、一番値が下がっているのはLSTATであることがわかります。rmse score = 4.98958 + 5.465154程度に悪化していると想定されます。
Feature Importanceでは重要度が一番高い特徴はRMでしたが、検証データではLSTATの方が影響が大きそうだとわかります。
逆に、ZNはシャッフルしても精度がほとんど落ちないので、影響がない特徴量と言えそうです。
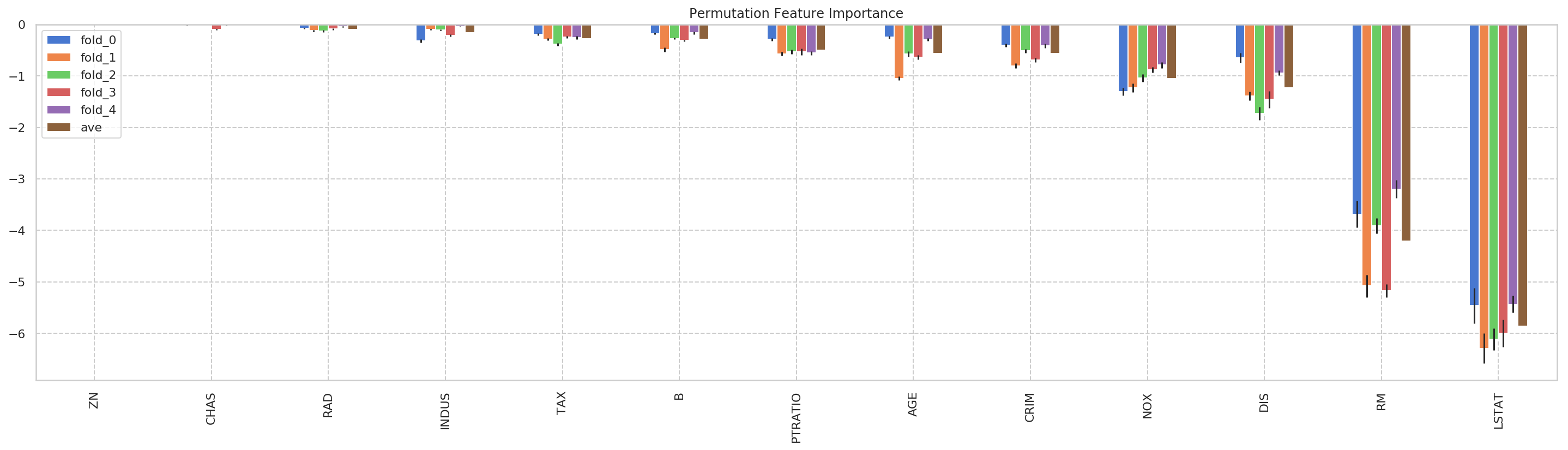
3-3. 5-foldのまとめ
5-foldの各foldのPermutation Importanceと、その平均値をグラフにプロットしました。ZNやCHAS,RADあたりはほとんど精度に影響しなさそうであることがわかりますね。
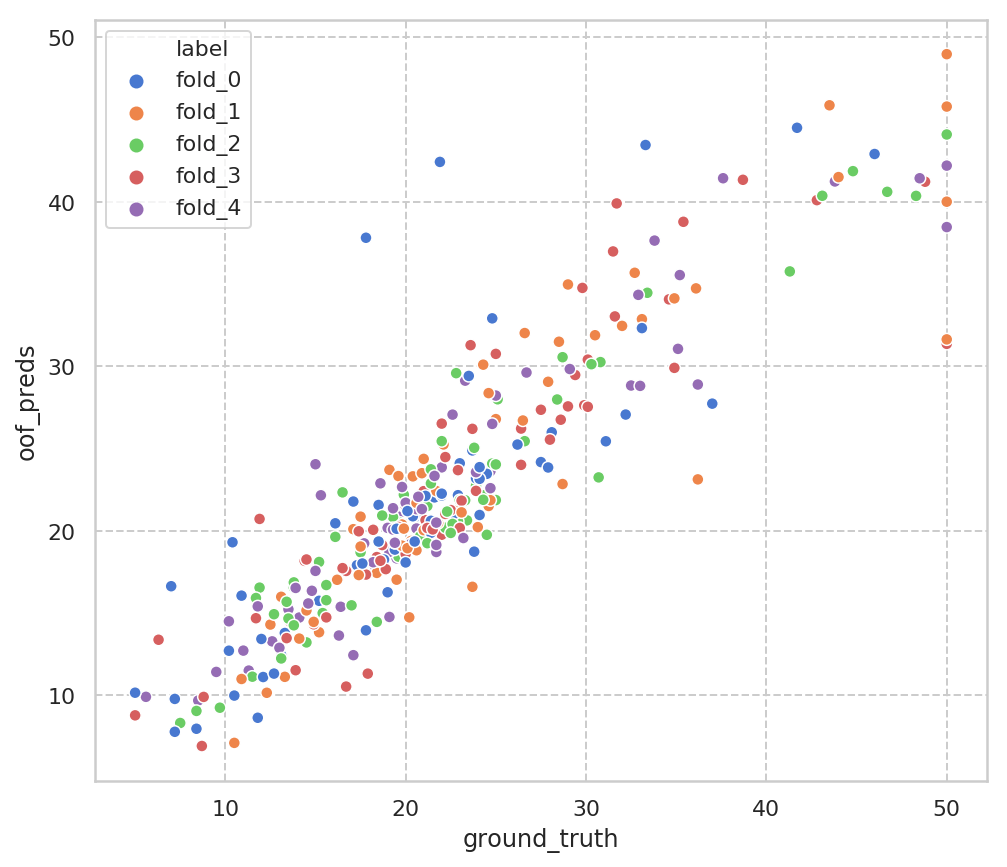
おまけ
fold毎のground_truthと予測値の比較のための散布図はこんな感じです。まぁまぁ予測可能な問題のようですね。ground_truthは50以上の値が切り捨てられていることもみて取れます。
追記
Permutation Importanceがうまくいかないケースはどのようなものか、というご質問をいただきましたので掲載させていただきます。
ちなみにこの手法が有効でない場合ってあるんでしょうか、つまり仮定(重要な特徴量ほどシャッフルした時にlossが下がる)が成り立たない場合。自分だとあんまり思いつかなくて💦
— triwave (@triwave33) December 9, 2019
kenmatsu4が思う回答
下記の2点、注意しながら使うのが良いかと思います。Permutation Importanceも特徴選択の銀の弾丸ではなく、複数の角度から検討して選ぶのが良いのだと思います。
注意1.多重共線性がある特徴セットの場合
木系のアルゴリズムを想定します。その場合、同等の効きの特徴があった場合、学習時にどちらの特徴を使ってsplitするか決められなくなる場合があると思います。(もしくはseedの揺らぎで確率的に選択される。subsampleなどの影響を受けそうですね) アルゴリズムに依存しますが、どちらの特徴かランダムで選択したり、列の先頭側を選ぶ2などで決定されます。
例えば相関1だとすると2つの特徴量が、学習時のsplitでランダムに分配されてしまうと、Feature Importanceのgainは按分されてしまいますし、predictするときも使われる回数が按分されます。本来相関1なら1つだけ残せばよく、1つにした場合に得られたgainは2つの特徴を合算させた値に近くなると思います。
学習時にすでにそのような状態になってしまうので、Permutation Importanceで学習済みモデルを利用するときに、一方の特徴は利用回数が少ないために本来より大きな影響があるはずのところ、影響が少なくなるケースがあると思います。
注意2. Cardinarityが高い場合
例えば、0, 1の2値をとり、含有率が50%-50%だとします。この特徴は、シャッフルしても変化がない行がかなり多くなることが想定され、結果あまり精度が下がらず、効きが悪い特徴に見えてしまいます。
その他いただいた回答
Twitterでこの件について話されていたものをピックアップしました。ありがとうございます。(不適切でしたら削除しますのでご連絡ください)
目に入ったので横から失礼します。多重共線性があるような特徴量のペアが特徴量セットに含まれる場合、importanceが過小評価されます。
— おなかへった (@ogatahetta) December 9, 2019
意図と違えばご放念ください。
その特徴量の量子化具合(というか取る値のdistinct count?)にimportanceが影響されるという記事をどこかで読みました。その特徴量の量子化が、他の特徴量と比べて粗いほどimportanceは低くなり、細かいほど高くなるらしいです。
— deeshi (@I_Need_Sunlight) December 9, 2019
探したらその記事が出てきました。こちらです。https://t.co/WAiZBjNL7s
— deeshi (@I_Need_Sunlight) December 9, 2019
その他、こんなことにも注意が必要、などのコメントありましたら教えていただけると嬉しいです!!!
参考
- Scikit-learn Permutation importance
https://scikit-learn.org/stable/modules/generated/sklearn.inspection.permutation_importance.html - 実行コード(Notebook)
https://www.kaggle.com/kenmatsu4/sklearn-permutation-importance
-
例えば、IEEE-CIS Fraud Detectionの1st solutionで使われている。 https://www.kaggle.com/c/ieee-fraud-detection/discussion/111308 ↩
-
このURLではrpartのCARTは最初の列を選ぶと言われています。 https://stats.stackexchange.com/questions/166560/cart-selection-of-best-predictor-for-splitting-when-gains-in-impurity-decrease/166914#166914 ↩