いつも乱数を生成しようとすると、どの関数を使えば良いか思い出せないので、使用頻度の高そうな乱数生成関数を備忘録としてまとめました。
特に後半の各種確率分布から生成される乱数はグラフとイメージを併記しているので、確率分布自体の理解にも役立つと思います。特にカイ二乗分布は自分も昔イメージがわかなくて悩んだので直感的にわかるよう説明をしてみました。
以下、下記のライブラリをimportしている前提で記載します。
import numpy as np
import numpy.random as rd
import scipy.stats as st
import matplotlib.pyplot as plt
一様分布系乱数#
rand(d0, d1, ..., dn)###
x = rd.rand(2, 3)
print x
[[ 0.49748253 0.88897543 0.65014384]
[ 0.68424239 0.19667014 0.83407881]]
[0, 1)の一様分布を生成。引数に生成乱数の次元の要素数を指定できる。上記例では2行3列となる。引数がない場合は1つの乱数を生成。
randn(d0, d1, ..., dn)
x1 = rd.randn(2, 4)
print x1
x2 = 2.5 * rd.randn(3, 3) + 3
print x2
[[-0.42016216 0.41704326 -0.93713613 0.23174941]
[-0.95513093 1.00766086 -0.5724616 1.32460314]]
[[-1.51762436 4.88306835 3.21346622]
[ 0.93229257 4.0592773 4.99599127]
[ 3.77544739 -0.20112058 2.47063097]]
平均0, 標準偏差1の正規分布から生成される乱数を生成。引数に生成乱数の次元の要素数を指定できる。上記例では2行4列となる。引数がない場合は1つの乱数を生成。
平均、標準偏差を指定したい場合はsigma * rd.randn() + muのように書く。
randint(low, high=None, size=None)
x = rd.randint(low=0, high=5, size=10)
print x
li = np.array([u"数学", u"理科", u"社会", u"国語", u"英語"])
for l in li[x]:
print l
[2 0 1 0 0 0 1 3 1 4]
社会
数学
理科
数学
数学
数学
理科
国語
理科
英語
引数で指定した範囲の離散一様分布から生成される整数の乱数を生成する。high, sizeは省略可。
highが省略されない場合は[0, low)、highが記載された場合は[low, high)の範囲が設定され、共に上限の値は含まないことに注意。
とある配列からランダムに要素を幾つか取り出したいときなどに有用。
random_integers(low, high=None, size=None)
x = rd.random_integers(low=1, high=10, size=(2,5))
print x
dice = rd.random_integers(1, 6, 100) # サイコロを100回振るシミュレーション
print dice
[[10 5 7 7 8]
[ 3 5 6 9 6]]
[4 5 2 2 1 1 6 4 5 5 5 5 1 5 1 1 3 2 4 4 5 3 6 6 3 3 5 3 6 1 1 4 1 1 2 1 1
5 1 6 6 6 6 2 6 3 4 5 1 6 3 1 2 6 1 5 2 3 4 4 3 1 2 1 1 3 5 2 2 1 4 1 6 6
2 5 4 3 2 1 4 1 2 4 2 5 3 3 1 4 4 1 6 4 1 1 3 6 1 6]
randint()同様、引数で指定した範囲の離散一様分布から生成される整数の乱数を生成する。high, sizeは省略可。
主な違いは範囲にあり、highが省略されない場合は[1, low]、highが記載された場合は[low, high]の範囲が設定され、「上限を含む」ということとlowのみ指定の場合の加減が"1"となるところ。
random_sample(size=None), random(size=None), ranf(size=None), sample(size=None)
x = np.random.random_sample((4,3))
print x
[[ 0.613437 0.38902499 0.91052787]
[ 0.80291265 0.81324739 0.06631052]
[ 0.62305967 0.44327718 0.2650803 ]
[ 0.76565352 0.42962876 0.40136025]]
タイトルの通り4種類ありますが、
http://stackoverflow.com/questions/18829185/difference-between-various-numpy-random-functions
によると、全部一緒です(random_sample以外はエイリアスです)。なんだそりゃ(笑)
rand()との違いは引数の指定の仕方がこれらはタプルで指定ですが、rand()は引数自体が複数ある、という指定の仕方になります。
choice(a, size=None, replace=True, p=None)
x1=rd.choice(5, 5, replace=False ) # 0-4の並べ替えと同等
print x1
x2=rd.choice(5, 5, p=[0.1,0.1,0.1,0.1,0.6]) # 4が出る確率が高い
print x2
[1 4 2 3 0]
[4 4 4 4 2]
choiceの引数の構造はchoice(a, size=None, replace=True, p=None)です。
aはrange(a)からの乱数選択を表します。
sizeで指定された数の乱数を生成します。
replaceが特徴的ですが、range(a)からサンプリングしたとみなされるのですが、Trueを指定すると取り出した数字を戻さない形で乱数生成されます。同じものが2回でないです。なのでaの数値がsizeより小さいとエラーになります。
pも特徴的ですが、一様乱数ではなく、各数字の生起確率を指定できます。なので、aとpのサイズを同じにしないとエラーになります。
今までの他の乱数はpython標準のlistで返しますが、これはnumpyのndarrayで戻り値を返します。
shuffle(x)
x = range(10)
rd.shuffle(x)
print x
[3, 4, 2, 5, 8, 9, 6, 1, 7, 0]
配列の順番をランダムにシャッフルする関数。戻り値で返すのではなく、引数に与えられた配列自体を変更することに注意。
permutation(x)
x1 = rd.permutation(10)
print x1
li = ['cat', 'dog', 'tiger', 'lion', 'elephant']
x2 = rd.permutation(li)
print x2
[4 0 6 5 3 8 7 1 9 2]
['elephant' 'tiger' 'lion' 'dog' 'cat']
引数にint型変数を指定すると、内部的にrange(a)を生成しそれをランダムに並び替える。
引数にlistを指定するとその要素をランダムに並び替える。listの中の値は数値でなく、文字列等のlistでも可。
uniform(low=0.0, high=1.0, size=None)
x = rd.uniform(-2,5,30)
print x
[-1.79969471 0.6422639 4.36130597 -1.99694629 3.23979431 4.75933857
1.39738979 0.12817182 1.64040588 3.0256498 0.14997201 2.0023698
3.76051422 -1.80957115 -0.2320044 -1.82575799 1.26600285 -0.27668411
0.77422678 0.71193145 -1.42972204 4.62962696 -1.90378575 1.84045518
1.06136363 4.83948262 3.57364714 1.73556559 -0.97367223 3.84649039]
一様分布から生成される乱数を生成。今まで説明した一様分布系の乱数生成関数と違うところは範囲を指定できるところ。引数構造は(low=0.0, high=1.0, size=None)で、[low, high)のように上が空いている半開区間。
確率分布モデル系乱数#
binomial(n, p, size=None) : 二項分布
x = rd.binomial(10, 0.5, 20)
print x
[5 4 5 5 4 3 8 3 6 6 3 4 5 1 5 7 6 4 2 6]
成功確率pの試行をn回行った場合の二項分布から生成される乱数を生成する。
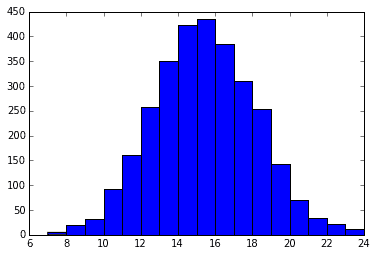
下記は確率0.5コイントスを30回行ってその回数をメモする、ということを3000回行った時のヒストグラムと考えることができる。
x = rd.binomial(30, 0.5, 3000)
plt.hist(x, 17)
poisson(lam=1.0, size=None) : ポアソン分布
x = rd.poisson(30, 20)
print x
[25 31 38 20 36 29 28 31 22 31 27 24 24 26 32 42 27 20 30 31]
単位時間当たりlam回発生する、というポワソン分布から乱数を生成する。
とある広告のクリック率を例にとると、その広告が1時間に30回クリックされる、というようなケースに適用。
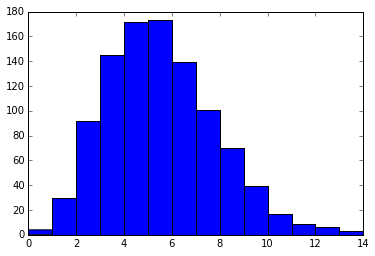
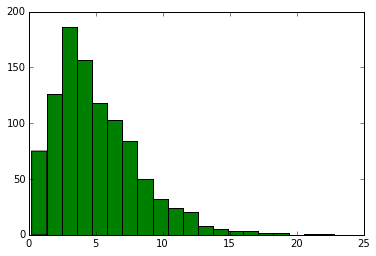
下記は1時間当たり平均5回クリックされる広告の試行を1000回行った時(=1000時間分のデータをとった)のヒストグラムの考えることができる。
x = rd.poisson(5, 1000)
plt.hist(x, 14)
hypergeometric(ngood, nbad, nsample, size=None) : 超幾何分布###
ngood, nbad, nsamp = 90, 10, 10
x = rd.hypergeometric(ngood, nbad, nsamp, 100)
print x
print np.average(x)
[ 9 10 8 9 8 7 7 9 10 7 10 9 9 8 9 9 9 9 8 10 5 10 9 9 9
9 9 10 10 8 10 9 9 9 7 9 9 10 10 7 9 9 10 10 8 9 10 10 8 10
10 9 9 10 9 10 8 9 9 9 8 9 10 9 10 10 10 9 9 9 10 9 8 10 7
7 10 10 9 10 10 9 10 9 7 9 9 8 8 10 7 8 9 10 9 9 10 9 8 10]
8.97
超幾何分布から生成される乱数を生成する。例えばngood個の良品とnbad個の不良品があって、そこからnsamp個を不良率調査で抜き出した時に取り出せた良品の個数を返す。
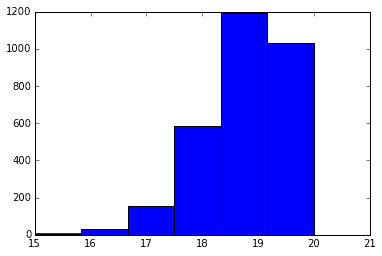
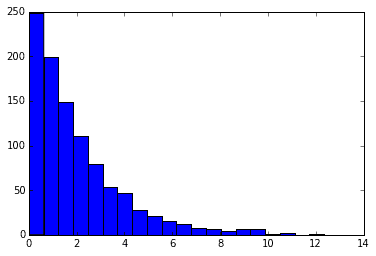
下記のグラフは、200個の製品が入っている集合箱に190個の良品、10個の不良品(つまり不良率5%)という状態だった時に、20個サンプリングして得られた良品の数をメモして、それを3000個の集合箱(全く同じ良品・不良品の数が入っている)に対して行った時のデータをヒストグラムにしたもの、と考えることができる。
ngood, nbad, nsamp = 190, 10, 20
x = rd.hypergeometric(ngood, nbad, nsamp, 3000)
plt.hist(x, 6)
geometric(p, size=None) : 幾何分布###
x = rd.geometric(p=0.01, size=100)
print x
[294 36 25 18 171 24 145 280 132 15 65 88 180 103 34 105 3 34
111 143 5 26 204 27 1 24 442 213 25 93 97 28 80 93 6 189
90 31 213 13 124 50 110 47 45 66 21 1 88 79 332 80 32 19
17 2 38 62 121 136 175 81 115 82 35 136 49 810 302 31 147 207
80 125 33 53 32 98 189 4 766 72 68 10 23 233 14 21 61 362
179 56 13 55 2 48 41 54 39 279]
幾何分布から生成される乱数を生成する。成功確率pの試行を成功するまで繰り返し実施した時に何回めで成功が出るか、という回数の乱数を返す。
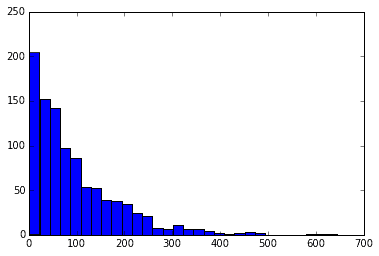
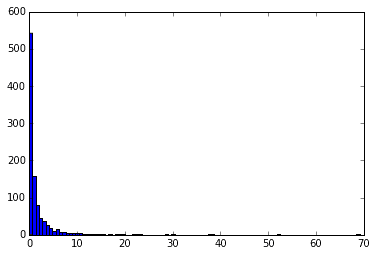
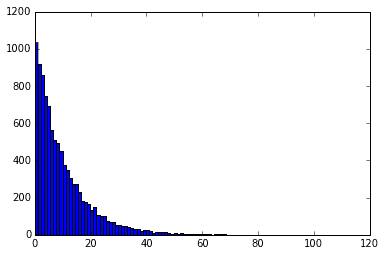
下記のグラフは、成功確率1%の試行を成功するまで繰り返し、成功までの回数をメモする。それを1000回繰り返した時のデータをヒストグラムにしたもの、と考えられる。
x = rd.geometric(p=0.01, size=1000)
plt.hist(x, 30)
normal(loc=0.0, scale=1.0, size=None) : 正規分布###
x = np.random.normal(5, 2, 20)
print x
[-0.28713217 2.07791879 2.48991635 5.36918301 4.32797397 1.40568929
6.36821312 3.22562844 4.16203214 3.91913171 6.26830012 4.74572788
4.78666884 6.76617469 5.05386902 3.20053316 9.04530241 5.71373444
5.95406987 2.61879994]
いわずもしれた確率分布の王道、正規分布から生成される乱数を生成します。locが平均、scaleが標準偏差を表します。
下記はそのヒストグラムです。
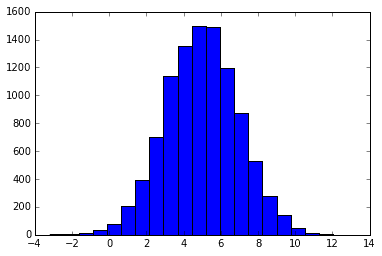
x = np.random.normal(5, 2, 10000)
plt.hist(x,20)
ちなみに、この次に紹介するカイ二乗分布から生成される乱数というのはこの正規分布から生成される乱数の組み合わせと2乗するという操作から作ることができます。
# 平均0, 標準偏差1の正規分布から生成される乱数を生成し、その値を2乗する
x1 = np.random.normal(0, 1, 10000)**2
x2 = np.random.normal(0, 1, 10000)**2
x3 = np.random.normal(0, 1, 10000)**2
x4 = np.random.normal(0, 1, 10000)**2
x5 = np.random.normal(0, 1, 10000)**2
x6 = np.random.normal(0, 1, 10000)**2
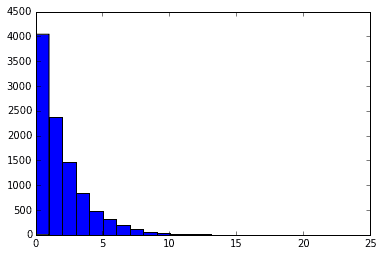
# その2乗した正規分布から生成された乱数を2つ足し合わせると自由度1のカイ二乗分布になる(青いグラフ)
plt.hist(x1+x2,20, color='b')
plt.show()
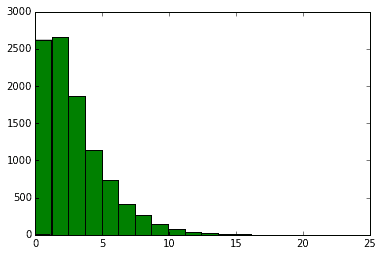
# また3つ足すと自由度2のカイ二乗分布(緑のグラフ)
plt.hist(x1+x2+x3,20, color='g')
plt.show()
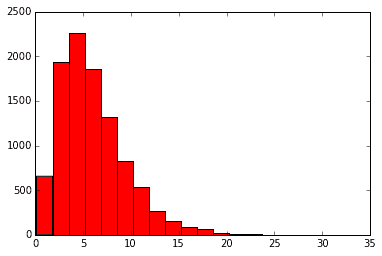
# さらに6つ足すと自由度5のカイ二乗分布(赤いグラフ)
plt.hist(x1+x2+x3+x4+x5+x6,20, color='r')
plt.show()
chisquare(df, size=None) : カイ二乗分布###
x = rd.chisquare(3, 20)
print x
[ 0.69372667 0.94576453 3.7221214 6.25174061 3.07001732 1.14520278
0.92011307 0.46210561 4.16801678 5.89167331 2.57532324 2.07169671
3.91118545 3.12737954 1.02127029 0.69982098 1.27009033 2.25570581
4.66501179 2.06312544]
自由度dfのカイ二乗分布から生成される乱数を返します。
一つ上の項でも触れたように、カイ二乗分布は標準正規分布から生成される乱数を2乗し、足し合わせたものが従う分布です。
# 自由度2, 5, 20に従うカイ二乗分布が生成する乱数のヒストグラム
for df, c in zip([2,5,20], "bgr"):
x = rd.chisquare(df, 1000)
plt.hist(x, 20, color=c)
plt.show()
f(dfnum, dfden, size=None) : F分布
x = rd.f(6, 28, 30)
print x
[ 0.54770358 0.90513244 1.32533065 0.75125196 1.000936 1.00622822
1.18431869 0.73399399 0.6237275 1.51806607 1.12040041 1.67777055
0.40309609 0.29640278 0.49408306 1.97680072 0.51474868 0.28782202
0.90206995 0.30968917 1.29931934 1.19406178 1.28635087 2.73510067
0.41310779 1.36155992 0.2887777 0.78830371 0.25557871 0.96761269]
2つの自由度dfnumとdfdenをもつF分布から生成される乱数を返します。このF分布は独立した2つのカイ二乗分布に従う確率変数を分子、分母に持つ(それぞれ自由度で割ったもの)からなる確率分布です。カイ二乗分布は正規化して2乗しているという意味で分散と見なせるので2つの分散が同じであることの検定に用いられます。
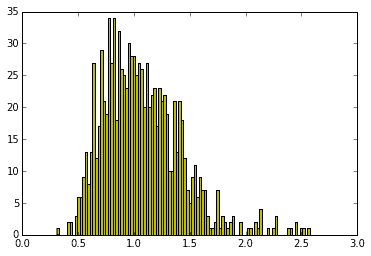
下記のグラフはそれぞれ自由度(1,4), (5,7), (10,10), (40,50)をもつF分布から生成された乱数をヒストグラムにしたものです。
for df, c in zip([(1,4), (5,7), (10,10), (40,50)], "bgry"):
x = rd.f(df[0], df[1], 1000)
plt.hist(x, 100, color=c)
plt.show()
exponential(scale=1.0, size=None) : 指数分布
lam = 0.1 # 1分あたり0.1回発生する。
x = rd.exponential(1./lam, size=20)
print x
[ 11.2642272 41.01507264 11.5756986 27.10318556 10.7079342
0.17961819 24.49974467 6.46388826 9.69390641 2.85354527
0.55508868 4.04772073 24.60029857 23.10866 19.83649067
12.12219301 10.24395203 0.16056754 8.9401544 8.86083473]
パラメータlamを持つ指数分布から生成される乱数を返す。lamは単位時間に発生する平均回数を示すパラメータ。exponentialに設定するときはlamの逆数をscaleに設定する。
exponentialは、単位時間に平均lam回起こる事象があるときに、次それが発生するまで何単位時間かかったかを表す乱数を返す。
つまり、1分に平均0.1回起きるような事象があった場合、3と出た場合は3分後にそれが起こったことを表してる。
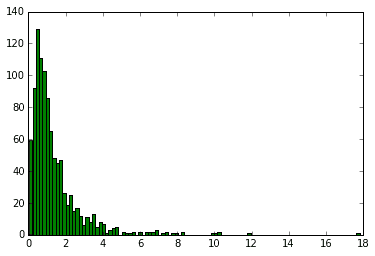
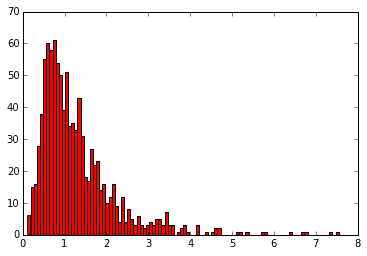
下記のグラフはlam=0.1のときに指数分布から生成される乱数をヒストグラムで表したもの。
lam = 0.1 # 1分あたり0.1回発生する。
x = rd.exponential(1./lam, size=10000)
plt.hist(x, 100)
参考にしたサイト#
numpyのリファレンスサイト
http://docs.scipy.org/doc/numpy/reference/routines.random.html