統計学、可視化してみるシリーズの続編です。
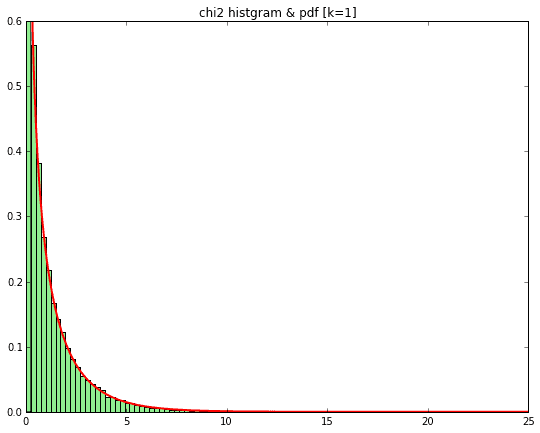
カイ二乗分布は、ABテストのカイ二乗検定等でよく使う分布です。$\chi^2$と書いてカイ二乗です。グラフにすると下記のような形で、自由度と呼ばれるkの値に応じて形が変化します。
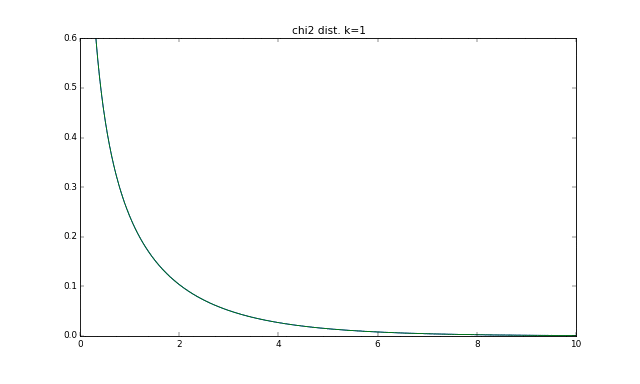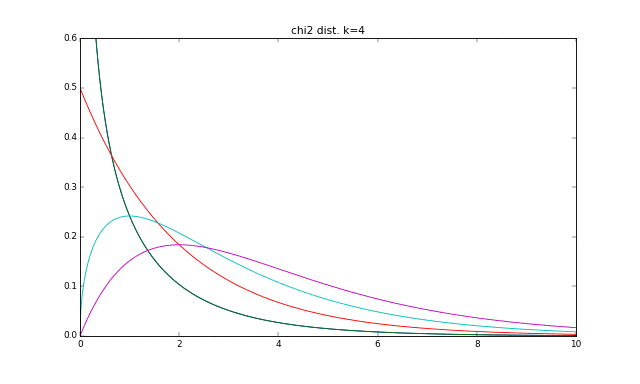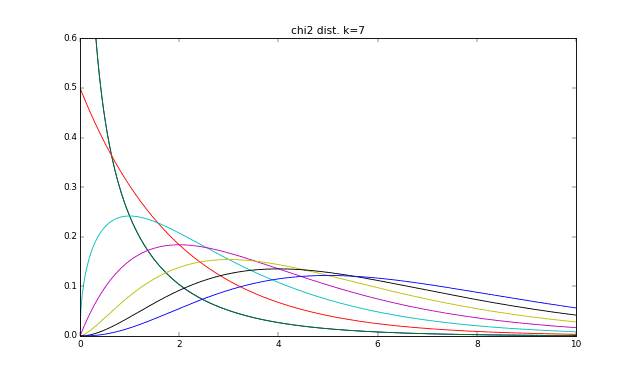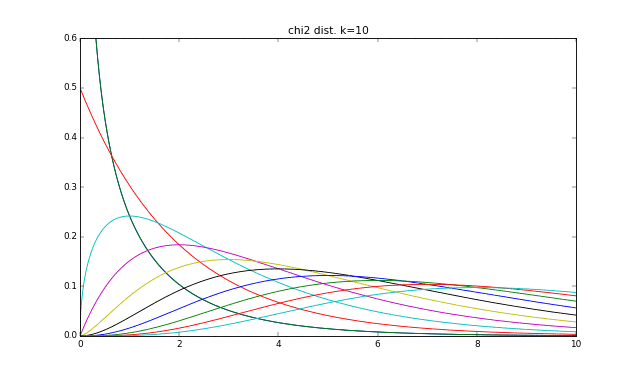
(グラフ描画のコードはこちら)
今回もWikipedia先生にカイ二乗分布の定義を聞いてみると、
独立に標準正規分布に従う $k$ 個の確率変数 $X_1, ..., X_k$ をとる。 このとき、統計量$$Z = \sum_{i = 1}^k X_i^2$$の従う分布のことを自由度 $k$ のカイ二乗分布と呼ぶ。
という返事が返ってきました。
うーん、どういうこと?正規分布の密度関数を2乗するの?どうやら違うようです。
まず、「独立に標準正規分布に従う $k$ 個の確率変数」ということなのでまずは標準正規分布に従う乱数のヒストグラムを書いてみようとおもいます。30,000個の$X \sim\ N(\mu, \sigma) $に従う乱数です。
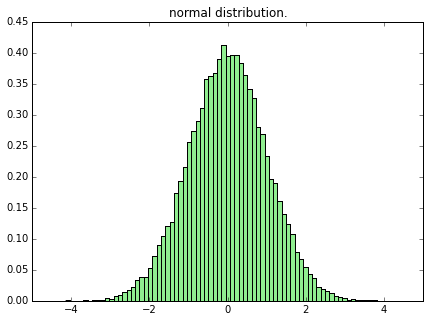
x = np.random.normal(0, 1, 30000)
plot_dist(x, bins=80, title="normal distribution.")
(グラフ描画のコード全文はこちら)
この乱数を2乗してプロットした乱数が従っている分布がカイ二乗分布なのです。コードで言うと
# 標準正規分布に従う乱数を30,000個生成
x = np.random.normal(0, 1, 30000)
# 生成した乱数を2乗する【【ここがキモ!!!】】
x2 = x**2
# ヒストグラムの描画
plt.figure(figsize=(7,5))
plt.title("chi2 distribution.[k=1]")
plt.hist(x2, 80, color="lightgreen", normed=True)
# 自由度1のカイ二乗分布の描画
xx = np.linspace(0, 25 ,1000)
plt.plot(xx, chi2.pdf(xx, df=1), linewidth=2, color="r")
となります。このグラフを表示すると下記になります。
2乗しているので、全てプラスになるので$x=0$よりすべて右にデータが移っていて、
2乗なので、
- $x<1$となる1より小さいところは0側に寄り、左におしつけられる
- $x\geq1$となる1より大きいところは∞側に寄り、右に引き伸ばされる
感じになります。(わかるかなこの説明で・・・^^;)
同時に自由度1のカイ二乗分布の密度関数の線を引いていますが、ほぼ一致しています!
これは標準正規分布に従う乱数を2乗してそのままプロットしているので、$X_1^2$をプロットしていることになります。$X$が1つなので自由度1のカイ二乗分布になるのです。
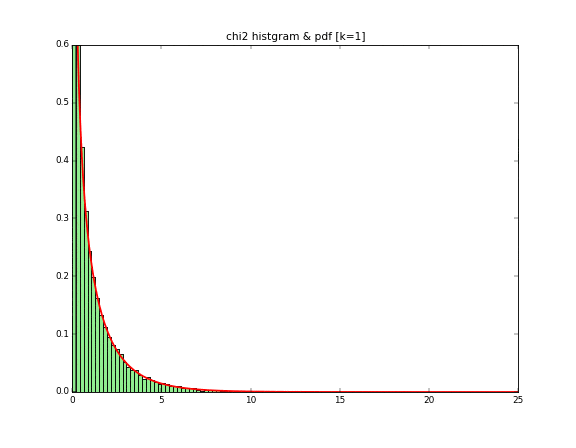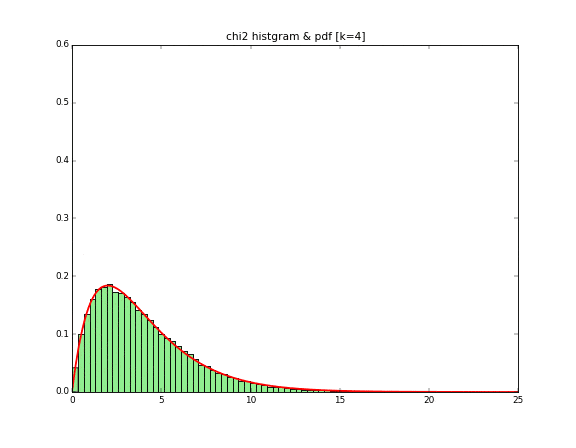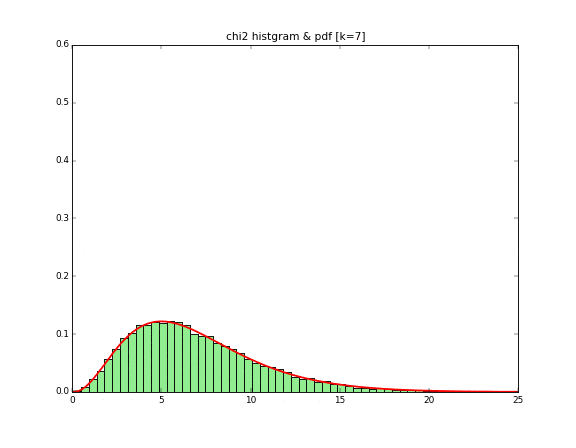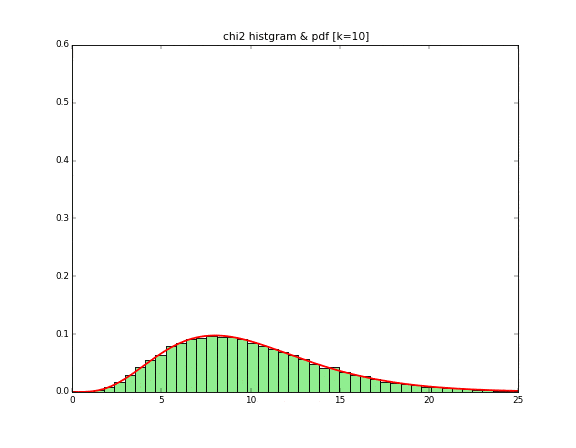
それでは、自由度2の$$X_1^2 + X_2^2$$から$$\sum_{i = 1}^{10} X_i^2$$までアニメーションにしてグラフを書いてみると下記になります。
こちらも完全に一致していますね!カイ二乗の「二乗」とは標準正規分布に従う乱数を2乗することと解釈ができますね!このイメージをヒストグラムを書くことでイメージをつけることができました!
下記がこの自由度1〜10までのグラフのアニメーション描画のコードです。
def animate(nframe):
n = 30000
k = nframe + 1
cum = np.zeros(n)
for i in range(k):
# 標準正規分布に従う乱数を30,000個生成
x = np.random.normal(0, 1, n)
# 生成した乱数を2乗する【ここがキモです!】
x2 = x**2
# 足し合わせた数が自由度となります。
cum += x2
# ヒストグラムの描画
plt.clf()
#plt.figure(figsize=(9,7))
plt.ylim(0, 0.6)
plt.xlim(0, 25)
plt.title("chi2 histgram & pdf [k=%d]"%k)
plt.hist(cum, 80, color="lightgreen", normed=True)
# 自由度1のカイ二乗分布の描画
xx = np.linspace(0, 25 ,1000)
plt.plot(xx, chi2.pdf(xx, df=k), linewidth=2, color="r")
fig = plt.figure(figsize=(10,8))
anim = ani.FuncAnimation(fig, animate, frames=10, blit=True)
anim.save('chi2_hist_dist.gif', writer='imagemagick', fps=1, dpi=64)
コードの補足###
gifアニメーションの描画にimagemagickを使っていますので、本家HPとPythonMagickを参考にインストールしてください。
ただ、このImageMagickとPythonMagickのインストールは環境により一苦労なので、手軽にアニメーションを作るだけであれば、下記のようにmp4であれば追加ライブラリなしにアニメーションが生成できます。
anim.save('filename.mp4', fps=13)