線形代数の勉強を始めると割とすぐ出てきますよね、内積。
計算自体はさほど難しくはないのだけれども、いまいちピンとこないという方、それなりにいるんじゃないでしょうか。私もそうでした。
なので、今回の可視化シリーズは「内積」にスポットを当ててみます。
また、統計学でもいたるところにも内積で理解できる事項が出てきて、「内積すげー」ってなります ![]() 。
。
ベクトルってデータの並びですので、統計学に非常に関連するんですね。統計学での扱われ方は次回からですが、まずは内積から。
#0.先に結論を少々#
ごにょごにょ前説が必要なので、内積の意味の結論だけ先にまず書きたいと思います。
内積は数式としては、下記のように書くことができます。
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
それを視覚的に表すと、下記のようになりベクトル${\bf a}$の長さに、ベクトル${\bf c}$の長さをかけたもの、という意味を持たせることができます。(${\bf c}$は、ベクトル${\bf b}$をベクトル${\bf a}$の上に射影したものです。)
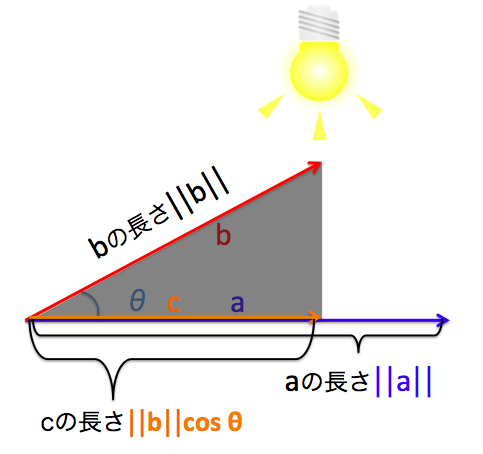
ここまでで、「うん、そうだよね」という方は、次回、統計学で内積がどのようにうまく扱われているかを説明部分しますので今しばらくお待ちください。
(スライド版にはすでに解説を入れているので、それまでは**こちら**をごらんください)
「なぜ、このように言えるのか」、「これがどういう事なのか」が知りたいという方は、これから説明していきたいと思いますので、そのまま下に進んでください。
#1.内積の定義と計算#
まずは最初に数式的な定義から入ります。
ベクトル${\bf a}=(a_1,\cdots,a_n), {\bf b}=(b_1,\cdots,b_n)$があったときに、その内積は下記のように定義されます。
{\bf a} \cdot {\bf b} = a_1b_1+\cdots+a_nb_n = \sum_{i=1}^n a_ib_i
それぞれのベクトルの要素の対応する要素(1つめの要素$a_1$と1つめの要素$b_1$を対応etc...)をかけて、全部足し合わせる、ということですね。これの視覚的意味を考えていきます。
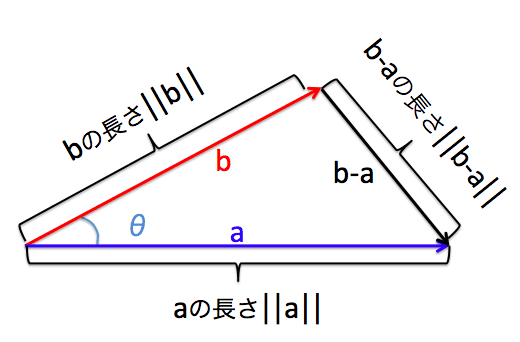
#2.余弦定理の適用#
内積を理解するために、余弦定理というものを使います。公式は下記です。
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ \cos\theta \cdots (*)
上記のような三角形の各辺の長さの関係がこの公式の関係を満たす、というものですね。
また、${\bf a}$の長さの2乗も
\|{\bf a}\|^2 = \left(\sqrt{a_1\cdot a_1 + \cdots + a_n\cdot a_n}\right)^2 =a_1\cdot a_1 + \cdots + a_n\cdot a_n\\
=\sum_{i=1}^n x_i^2 = {\bf a} \cdot {\bf a}
のように、同じベクトルの内積で表すことができます。
これを$||{\bf b}-{\bf a}||^2$に適用すると、
\|{\bf b}-{\bf a}\|^2 = ({\bf b}-{\bf a})\cdot({\bf b}-{\bf a}) = {\bf a}\cdot{\bf a} + {\bf b}\cdot{\bf b} - 2 {\bf a}\cdot{\bf b} \\
= \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b}
これを余弦定理の(*)式に代入すると、
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
\Rightarrow \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b} = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
両辺に$||{\bf a}||^2 + ||{\bf b}||^2$があるので消去して、
- 2 {\bf a}\cdot{\bf b} = - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta \\
\Rightarrow {\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ cos\theta
ということで、内積は
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
であることがわかりました。
わ、わかりました・・・???
だから何?って感じですよね・・・
でも、この形がひじょーに重要なので、ぜひ覚えておいてください。
次に、この$||{\bf a}||||{\bf b}||\ \cos\theta$が何者かを見ていきます。
#3.||a|| ||b||cosθの謎を探る#
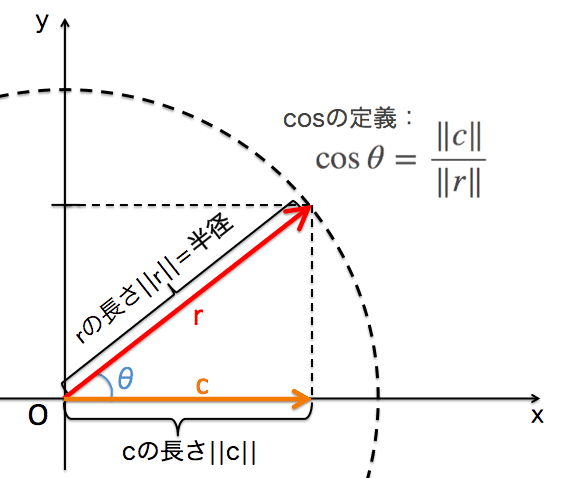
##3.1 cos θ の再確認と射影という概念 ##
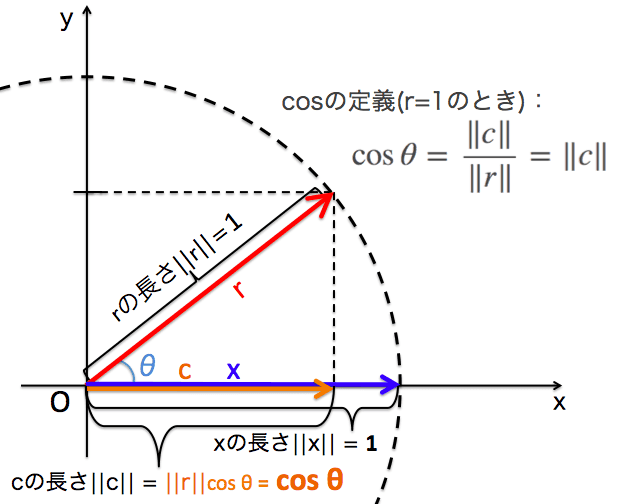
まず、$\cos \theta$を今一度きちんと再確認したいと思います。
数式的な定義は、
\cos \theta = \frac{\|c\|}{\|r\|}
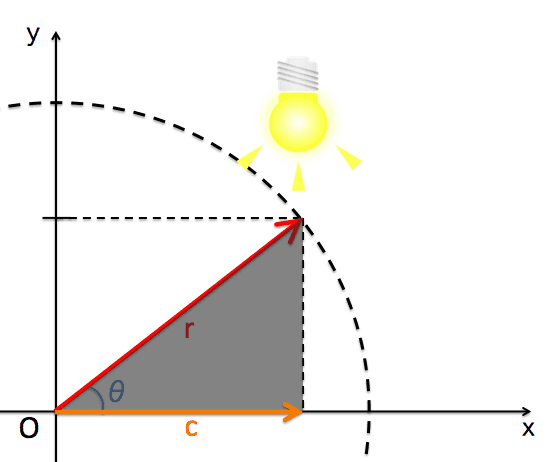
$r$は半径で、$x$はベクトル$r$からx軸に垂直な線を引いて、その点までのベクトルです。イメージとしては、下のように、真上からライトを照らして影となる部分ですね。(射影と言ったりします。)
屋根${\bf r}$にライトを当ててできる影の部分がベクトル${\bf c}$です。
##3.2 内積の意味 ##
$\cos \theta = ||c||\ /\ ||r||$ の両辺に$||r||$をかけて、分母の $||r||$ を反対側の項に移すと、
\|c\| = \|r\|\cos \theta
になるので、cの長さは$||r||\cos \theta$であるとみなすことができます。屋根の長さに$\cos \theta$をかけたものと考えられます。
さて、ここで前項の宿題となっていた
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
に話を戻します。同様に上からライトを当ててみます。
ベクトル${\bf b}$からベクトル${\bf a}$上に射影してできたベクトルを${\bf c}$とするとその長さは、先ほどのロジックを当てはめると「屋根の長さに$\cos \theta$をかけたもの」なので、$||{\bf b}|| \cos \theta$になります。
これで必要な材料は揃いました。
内積${\bf a}\cdot{\bf b}$は
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
ですので、**「ベクトル${\bf a}$の長さ」と、「ベクトル${\bf b}$をベクトル${\bf a}$上に射影したものの長さ」**の積と考えられるのです。
内積も**「積」**というくらいなので、なんらかの掛け算なのですが、ベクトル同士の掛け算は方向を合わせて、その長さを掛け算するというイメージで良いのではないかと私は考えています。
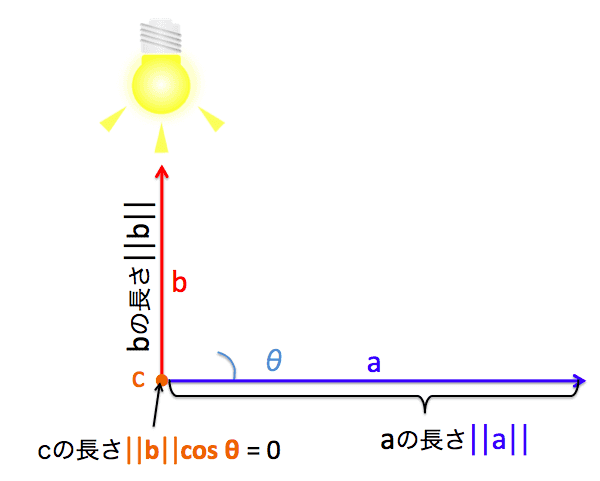
###3.3 2つのベクトルの方向が垂直の時###
2つのベクトルの角度が直角の場合、上からライトを当てても影ができないですね。なので、このときベクトル${\bf c}$の長さが0になってしまいます。つまり、角度が直角のときは内積も0になるのです。
##3.3 長さ1のベクトルの場合 ##
話をもっと簡単にして、$||r||=1, ||x||=1$だったとします。$\cos \theta$の定義は
\cos \theta = \frac{\|c\|}{\|r\|} = \|c\|
ですので、${\bf c}$の長さがそのまま$\cos \theta$の値になります。
さて、${\bf x}$と${\bf r}$の内積を見てみると、
{\bf x}\cdot{\bf r} = \|{\bf x}\|\|{\bf r}\|\ \cos\theta = 1 \cdot 1 \cdot \cos\theta = \cos\theta
という計算になりますので、**長さが1同士の2つのベクトルの内積は$\cos \theta$**になります ![]()
次回の記事で、「統計学で内積が利用されるシーン」について書く予定です。分散・標準偏差、共分散・相関係数、回帰係数などがこの内積との関連でどのように見えるかをPythonによるグラフ、アニメーションを用いて説明する予定です。