今回は2つのテーマが合わさった記事になっていまして、ひとつはPythonからRのパッケージを呼び出して利用する方法、もうひとつが密度比推定のRパッケージdensratioを使って異常検知をしてみる、という記事です。
Rはとても多くの統計手法のパッケージが公開されており(8000を超えてるとか)、PythonにはないものもRには存在したりするので、非常に魅力的です。しかし、Pythonに慣れている人は、データの前処理やグラフ描画は慣れ親しんだPythonで行いたいと考えてしまうのではないでしょうか?(自分のことです ![]() )そんな人のために、PythonからRのパッケージを使う方法をご紹介します。
)そんな人のために、PythonからRのパッケージを使う方法をご紹介します。
Pythonソースコードの全文はGitHubのココに置いてありますので、適宜ご利用ください。
環境
試した環境は下記です。MacとAnacondaで試しています。Anacondaを導入していれば特に準備は不要です。本記事の内容は基本的にJupyter Notebook(iPython Notebook)にて検証を行っています。
Python 3.5.1 |Anaconda custom (x86_64)| (default, Dec 7 2015, 11:24:55)
[GCC 4.2.1 (Apple Inc. build 5577)] on darwin
IPython 5.0.0
RのパッケージをPythonから呼び出す
準備
まず前提としてRがインストールされていることが必要です。その上で一度R(またはRStudio)を起動し、densratioパッケージを下記のようにインストールしておいてください。密度比推定に使います。一度インストールが終わったらRは終了してもOKです。
install.packages("densratio")
PythonからRにアクセスする
PythonからRにアクセスするためにrpy2というライブラリをインストールします。
pip install rpy2
このrpy2を使ってRにアクセスしていきます。まずは各種インポートします。これでRのオブジェクトが使えること、PandasのデータフレームとRのデータフレーム変換することができるようになります。
from rpy2.robjects.packages import importr
import rpy2.robjects as robjects
# import pandas.rpy.common as com # [depricated]
from rpy2.robjects import pandas2ri
pandas2ri.activate()
密度比推定パッケージdensratioを試す
親分@hoxo_m さん製パッケージ densratioを使って密度比推定と、それを用いた異常検知を試してみます。
早速RのdensratioパッケージをPythonで読み込んでみますが、下記の通り1行書くだけでインポートできてしまいます。
densratio = importr("densratio")
1次元のデータで試す
密度比推定は、共変量シフトと呼ばれる入力変数の分布が訓練データとテストデータで異なる時に、それぞれの分布を推定してからその比を取るのではなく、直接密度の比を推定する方法です。
(共変量とは入力変数のこと)
訓練データ$\mathcal{D}= \{ \boldsymbol{x}^{(1)}, \cdots, \boldsymbol{x}^{(N)} \}$は正常なデータのみ(もし異常データがあったとしてもそれあごくごく少数)とし、テストデータ$\mathcal{D}'= \{ \boldsymbol{x}^{'(1)}, \cdots, \boldsymbol{x}^{'(N')} \}$には一定数の異常データが含まれており、この異常データを密度比から検知します。
訓練データの分布を$p_{tr}(\boldsymbol{x})$、テストデータ分布を$p_{te}(\boldsymbol{x})$とすると、密度比とは
w(\boldsymbol{x}) = {p_{tr}(\boldsymbol{x}) \over p_{te}(\boldsymbol{x})}
と表される値です。この$w(\boldsymbol{x})$の推定値$\hat{w}(\boldsymbol{x})$を
\hat{w}(\boldsymbol{x}) = \sum_{l=1}^{N} \alpha_l \varphi_l (\boldsymbol{x})
とし、基底関数$\{\varphi_l (\boldsymbol{x}) \}_{l=1}^{N}$の線形結合で表す。ここで$\varphi_l (\boldsymbol{x}) $は基底関数とよばれ、今回はこの基底関数にRBFカーネル
\varphi_l (\boldsymbol{x}) = \exp \left( { \| \boldsymbol{x} - \boldsymbol{x}^{l}\|^2 \over 2\sigma^2} \right)
を使います。$\boldsymbol{x}^{l}$は$l$番目の訓練データを表しますので、訓練データを中心とした正規化定数を省略した正規分布のような形になります。
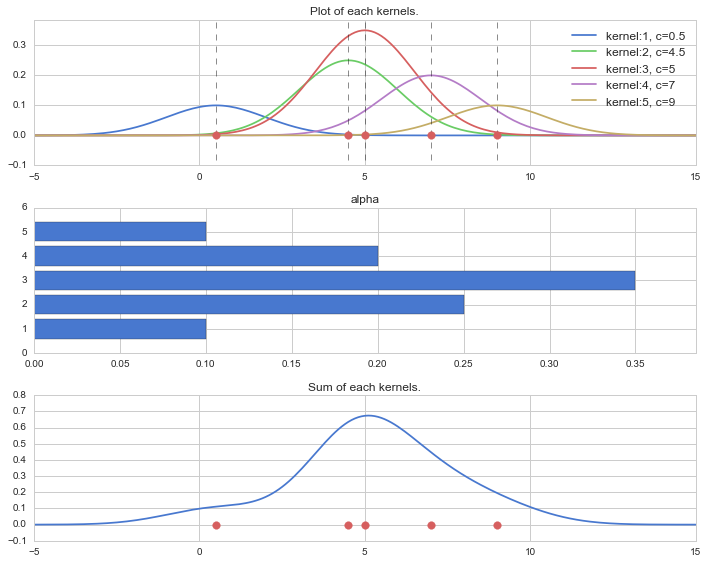
下記は一例で、5つの訓練データ[0.5, 4.5, 5.0, 7.0, 9.0]があったとしてそこから、α=[ .1, .25, .35, .2, .1]で重み付けしたカーネルを足し合わせ、下段でそれが推定された密度比$\hat{w}(\boldsymbol{x})$として表される様子を示しています。
なのでこの密度比推定は、カーネルの混合比率 $\boldsymbol{\alpha}$ を決める問題になります。カーネルの幅を示す $\sigma$ はハイパーパラメーターとなり、これはクロスバリデーションなどで決定します。
なぜこれがうまくいくか、またどうやって $\boldsymbol{\alpha}$ を決めるか、については参考にあげた書籍やページ、論文をご参考ください。
人工データの生成
通常の外れ値問題は、テストデータつまり新しいデータは1個得られたとして個別に異常度を計算して閾値と比較しますが、この手法はテストデータは複数の標本である点が特徴的です。まずこのデータを乱数を用いて人工的に生成します。
また、densratioはRのパッケージなのでpandas2ri.py2riをつかってPandasの世界からRの世界にデータを移し替えます。
rd.seed(71)
n_data1 = 3000
n_data2 = 500
m = [1, 1.2]
sd = [1/8, 1/4]
x = rd.normal(loc=m[0], scale=sd[0], size=n_data1)
y = rd.normal(loc=m[1], scale=sd[1], size=n_data2)
# PythonのデータフレームをRのデータフレームに変換!
r_x = pandas2ri.py2ri(pd.DataFrame(x))
r_y = pandas2ri.py2ri(pd.DataFrame(y))
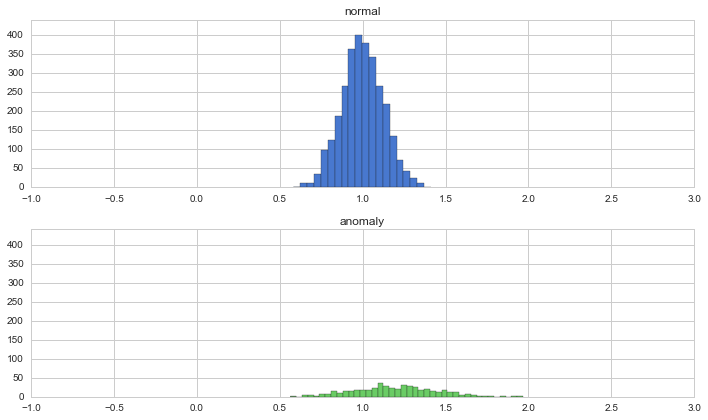
異常データは正常データに比べ、平均が少し高く、分散が大きいデータにしています。
密度比推定を実行する
このデータに対しdensratioを用いて密度比を算出します。このパッケージでは密度比推定法は2種類使うことができ、カルバックライブラー情報量を用いて密度比を推定するKLIEPと、非制約最小二乗密度比推定法を用いたuLSIFを使うことができます。今回はデフォルトでもある、高速に計算ができるuLSIFを使います。
Rのデータフレームに変換したr_x, r_yをこの関数に突っ込むだけです。便利ですね ![]()
(今回$\sigma$はクロスバリデーションかけずに決め打ちで0.2としました)
result = densratio.densratio(r_x, r_y, "uLSIF",0.2, "auto")
この処理の途中にWarningメッセージが表示されますが、Warningではなくクロスバリデーションでハイパーパラメーターを決める過程のログなのですが、rpy2の仕様でWarningとして表示されてしまいます。
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: ################## Start uLSIF ##################
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Searching optimal sigma and lambda...
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.001, score = 11.113
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.003, score = 1.026
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.010, score = -0.654
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.032, score = -0.931
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.100, score = -1.009
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.200, lambda = 0.316, score = -1.029
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Found optimal sigma = 0.200, lambda = 0.316.
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Optimizing alpha...
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: End.
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: ################## Finished uLSIF ###############
warnings.warn(x, RRuntimeWarning)
結果から密度比を取り出す関数であるcompute_density_ratioを、Python側に取り出して実行します。まず、正常標本に対する推定した密度比w_hatを取得します。また、密度比を$\hat{w}$とすると、異常度はその対数のマイナス
a(\boldsymbol{x}^{'(n)}) = -\ln \hat{w}(\boldsymbol{x}^{'(n)})
で表現するので、この変換を行い算出します。
また、この訓練データの分布の99%パーセンタイルを異常の閾値として、異常判定を行ってみたいと思います。
# 密度比を計算して取り出す
compute_density_ratio = get_method(result, "compute_density_ratio")
w_hat = compute_density_ratio(r_x)
# 密度比を異常度に変換
anom_score = -np.log(w_hat)
thresh = np.percentile(anom_score, 99) # 正常標本の密度比の99%パーセンタイルを異常を判定する閾値と設定
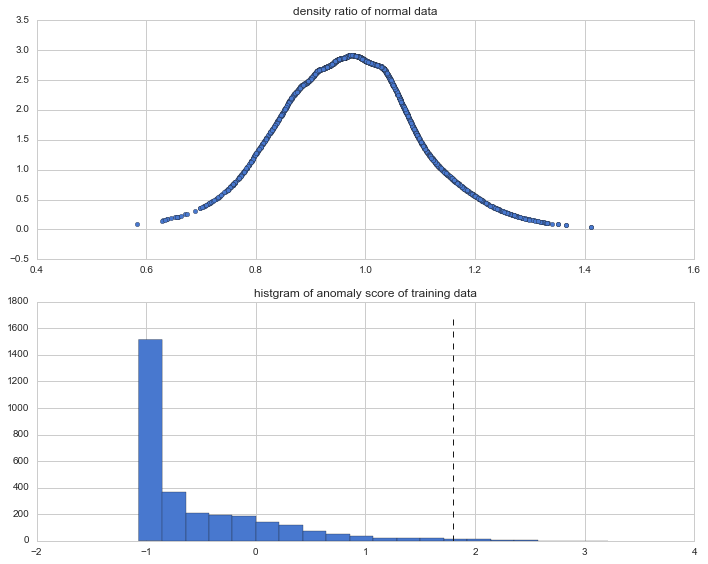
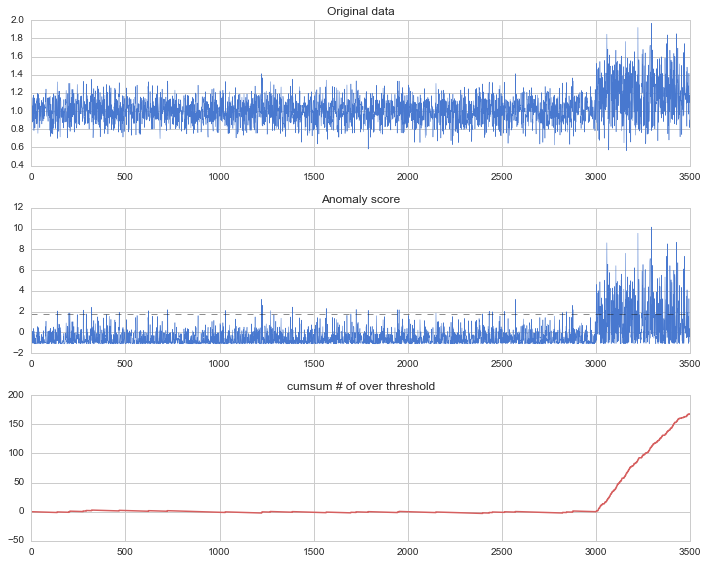
このw_hatとanom_scoreをプロットしたものが下記です。
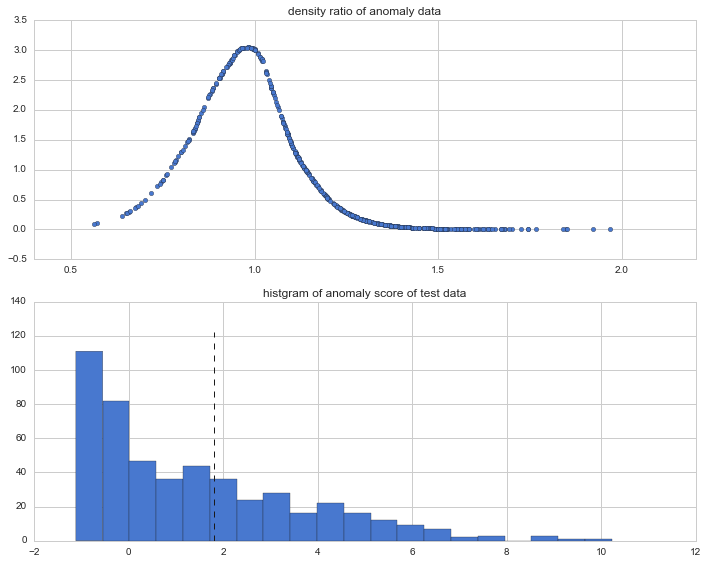
次に今度はテストデータの密度比と、異常度のヒストグラムを計算して描画します。
# 結果からcompute_density_ratioを取り出して実行。テストデータに対する推定した密度比を取得する。
compute_density_ratio = get_method(result, "compute_density_ratio")
w_hat = compute_density_ratio(r_y)
# 密度比を異常度に変換
anom_score = -np.log(w_hat)
テストデータの方が異常の閾値を超えているデータが多いことがわかります。
元データと異常度を比較し、かつ異常度の閾値を超えたデータの数を数えて積み重ねたデータを見てみましょう。(ただし閾値に設定したパーセンタイルを引くことで、正常時は平均0になるようにします)このデータを時系列データと見立てると、最初の方はほぼ正常であまり閾値を超えることがないのですが、後半データの傾向が変わり急に異常度の高いデータが増えていることがわかります。
2次元の入力変数の場合
さて次に入力変数が2次元だった場合を試してみます。
データは @oshokawa さんのスライド
https://speakerdeck.com/oshokawa/mi-du-bi-tui-ding-niyoruyi-chang-jian-zhi
と同じ仕様で作成してみました。
# 訓練データの生成
rd.seed(71)
cov_n = [[ 10, 0],
[ 0, 10]]
M = 2
m_n_1 = (10, 10)
m_n_2 = (20, 20)
n_data = 500
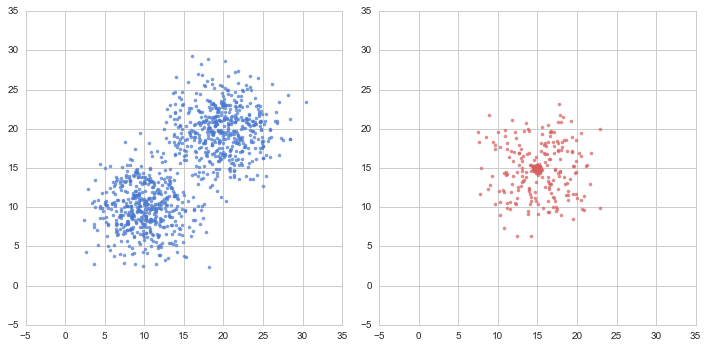
X_norm = np.empty((2*n_data, M))
X_norm[:n_data] = st.multivariate_normal.rvs(mean=m_n_1, cov=cov_n, size=n_data)
X_norm[n_data:] = st.multivariate_normal.rvs(mean=m_n_2, cov=cov_n, size=n_data)
N_norm = 2*n_data
# テストデータの生成
cov_n_1 = [[ 5, 0],
[ 0, 5]]
cov_n_2 = [[ .1, 0],
[ 0,.1]]
m_n_1 = (12.5, 12.5)
m_n_2 = (17.5, 17.5)
m_n_3 = (15, 15)
m_n_4 = (17.5, 12.5)
m_n_5 = (12.5, 17.5)
n_data_a = 50
N_anom = 5*n_data_a
X_anomaly = np.empty((n_data_a*5, M))
for i, m, c in zip(range(5), [m_n_1,m_n_2,m_n_3,m_n_4,m_n_5], [cov_n_1,cov_n_1,cov_n_2,cov_n_1,cov_n_1]):
X_anomaly[n_data_a*i:n_data_a*(i+1)] = st.multivariate_normal.rvs(mean=m, cov=c, size=n_data_a)
X = np.r_[X_norm, X_anomaly]
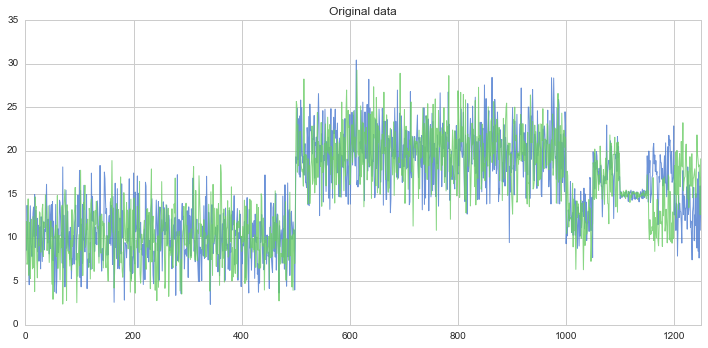
こんな感じのデータです。ある機械が低速回転モードと高速回転モードをもち、その状態が途中で変わるのですが、最後の方動きが怪しくなっている、といったデータをイメージされて作られています。
1次元のデータのときと同様、Rのデータフレームに変換した上で、densratioにかけます。
# Rのデータフレームに変換
r_x = pandas2ri.py2ri(pd.DataFrame(X_norm))
r_y = pandas2ri.py2ri(pd.DataFrame(X_anomaly))
r_xall = pandas2ri.py2ri(pd.DataFrame(X))
# 密度比推定を実行
result = densratio.densratio(r_x, r_y)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: ################## Start uLSIF ##################
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Searching optimal sigma and lambda...
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.001, lambda = 0.001, score = 0.000
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.001, lambda = 3.162, score = -0.000
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.032, lambda = 0.001, score = -0.000
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.100, lambda = 0.001, score = -0.002
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 0.316, lambda = 0.001, score = -0.352
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: sigma = 1.000, lambda = 0.010, score = -2.466
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Found optimal sigma = 1.000, lambda = 0.010.
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: Optimizing alpha...
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: End.
warnings.warn(x, RRuntimeWarning)
//anaconda/lib/python3.5/site-packages/rpy2/rinterface/__init__.py:185: RRuntimeWarning: ################## Finished uLSIF ###############
warnings.warn(x, RRuntimeWarning)
密度比を取り出し異常度を計算、訓練データから閾値を設定する、という流れは今回も同じです!
# 推定した密度比を取得する
compute_density_ratio = get_method(result, "compute_density_ratio")
w_hat = np.asanyarray(compute_density_ratio(r_xall))
# 異常度閾値
anom_percentile = 5 # 推定した密度比の下側5%以下を異常とする
# 訓練データのうち、指定したパーセンタイル以下を異常とする閾値を設定
anom_score = w_hat[:len(X_norm)]
thresh = np.percentile(anom_score, anom_percentile)
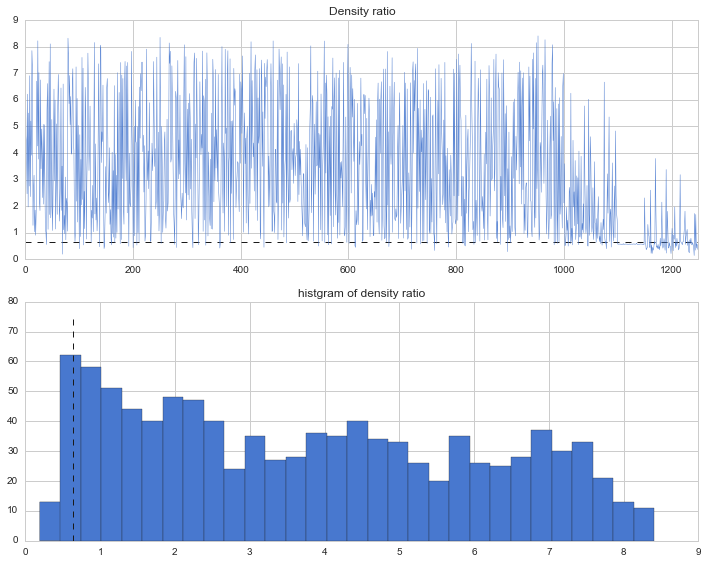
訓練データの密度比を異常度に変換してグラフにします。同じく、訓練データの指定パーセンタイル(今回は95%点)を閾値として異常判定を行います。
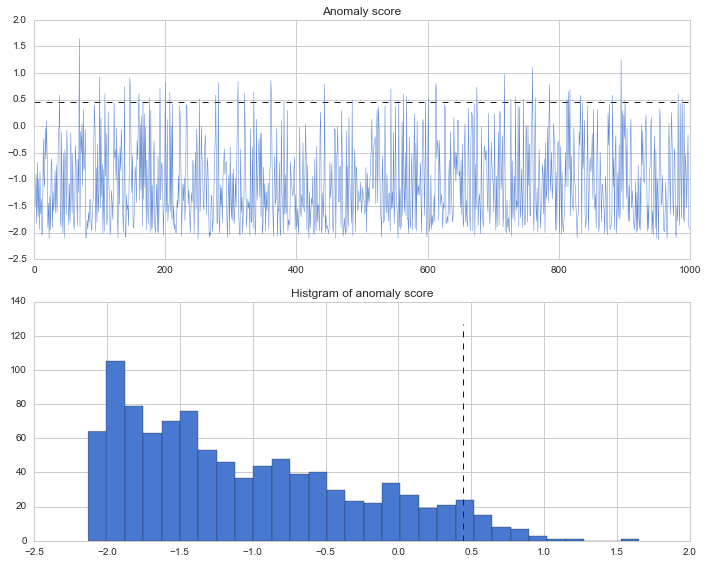
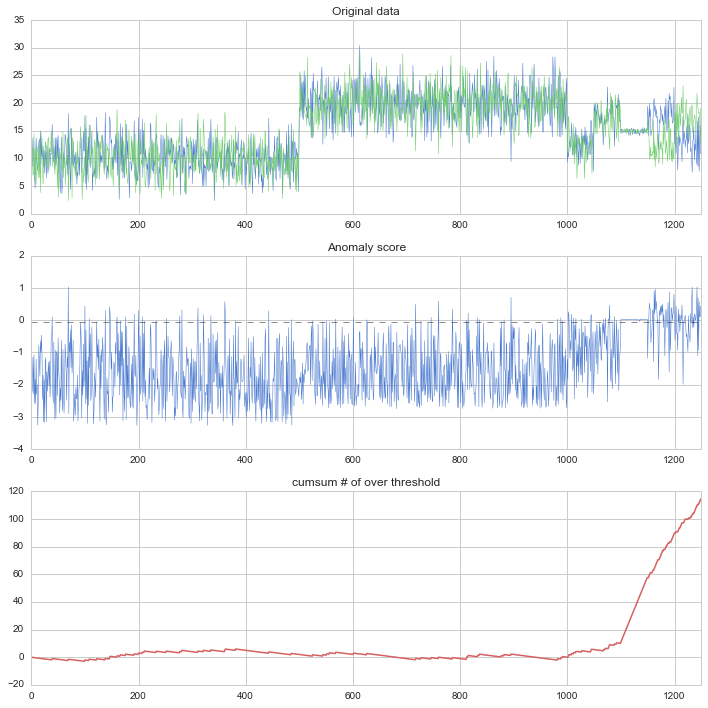
計算した閾値を元に、全データの異常度と、閾値を超えたデータの数を数えて傾向を見てみます。やはり後半の様子がおかしいところで異常度が上がっていますね。
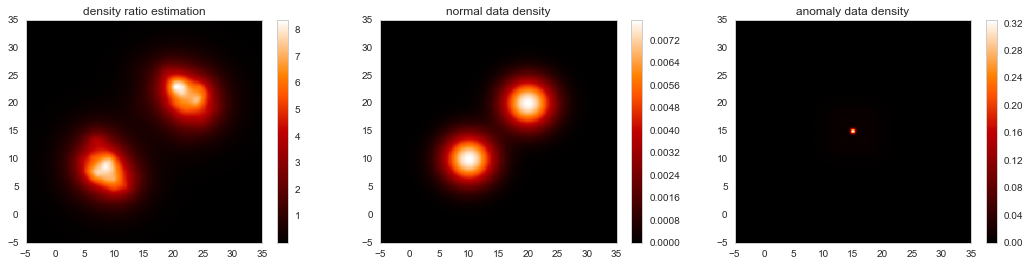
最後に推定した密度をヒートマップでみてみます。左が密度比の推定値、真ん中が訓練データの密度、右がテストデータの密度になります。
参考
このページのソースコード全文
(グラフ描画コードなど、本記事中では端折った箇所もこちらには記載されています。)
https://github.com/matsuken92/Qiita_Contents/blob/master/General/Density_ratio_R.ipynb
rpy2パッケージリファレンス
http://rpy2.readthedocs.io/
densratioパッケージ (@hoxo_m )
https://github.com/hoxo-m/densratio
密度比推定による異常検知 (@oshokawa)
https://speakerdeck.com/oshokawa/mi-du-bi-tui-ding-niyoruyi-chang-jian-zhi
「異常検知と変化検知」 井手剛、杉山将著 (機械学習プロフェッショナルシリーズ)
https://www.amazon.co.jp/dp/4061529080
密度比推定を用いた特異点検出手法
http://2boy.org/~yuta/publications/ibis2007.pdf