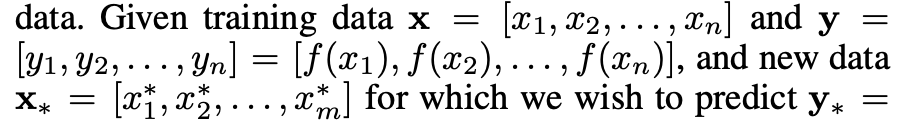概要
秘密計算を使ってガウス過程回帰を実装している応用系論文について見てみます。
みていくのは2つの論文です。
- Privacy-Preserving Gaussian Process Regression – A Modular Approach to the Application of Homomorphic Encryption (2020)
- Practical Privacy-Preserving Gaussian Process Regression via Secret Sharing (2023)
の二つです。
ガウス過程回帰についておさらい
まずはガウス過程回帰についておさらいしてみます。
1つ目の論文の2章に書かれている、ガウス過程のおさらいをそのまま借用します。
つまり、学習データセットに対して巨大な共分散行列を計算しておくこと、
そして入ってきたテストデータ(学習時にはみたことのないデータ)に対して、
学習データとの共分散行列を計算、
また、テストデータ同士の共分散行列を計算する必要があります。
それらが計算できたら、予測される回帰データの平均と分散は、
逆行列などの計算と、行列同士の積を計算することで可能だということです。
ここで、逆行列はKに対して、つまり学習データの共分散行列に対してのみ計算が必要です。
今日分散行列の要素としては、ガウシアンカーネルがよく使われ、
ガウシアンカーネルについては、二つのデータが近ければ値が大きくなる様に設定され、
遠ざかるにつれてエクスポネンシャルスケールで値が小さくなる様な関数です。
Privacy-Preserving Gaussian Process Regression – A Modular Approach to the Application of Homomorphic Encryption
IBM Research から2020年に発表された論文です。
準同型暗号を用いたアプローチです。
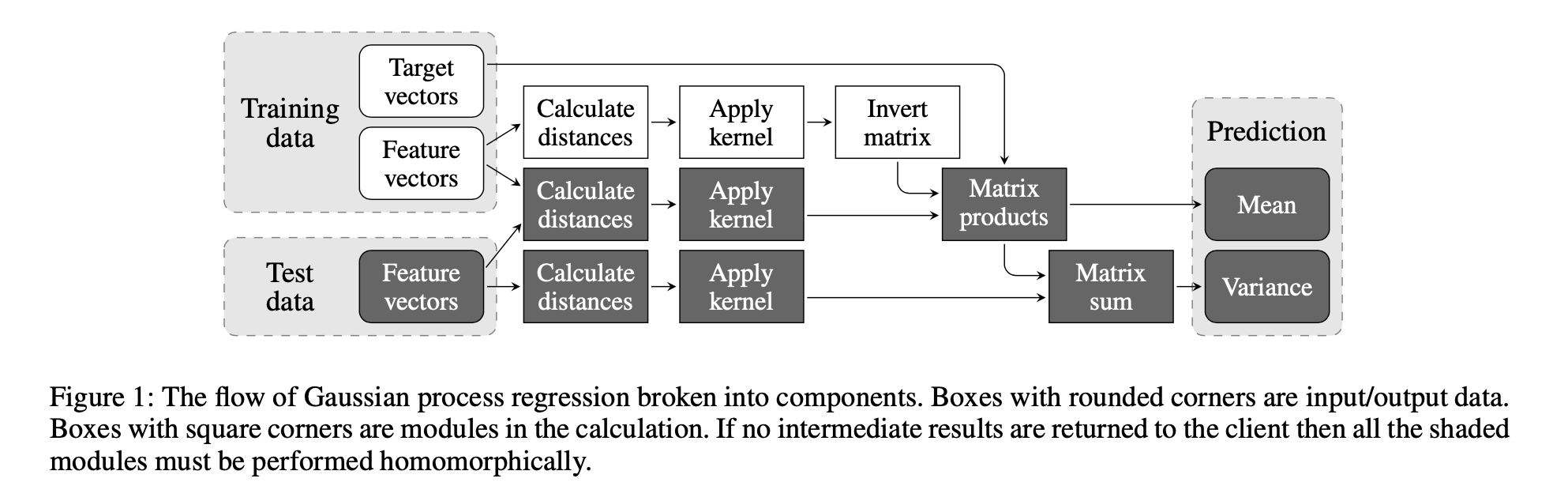
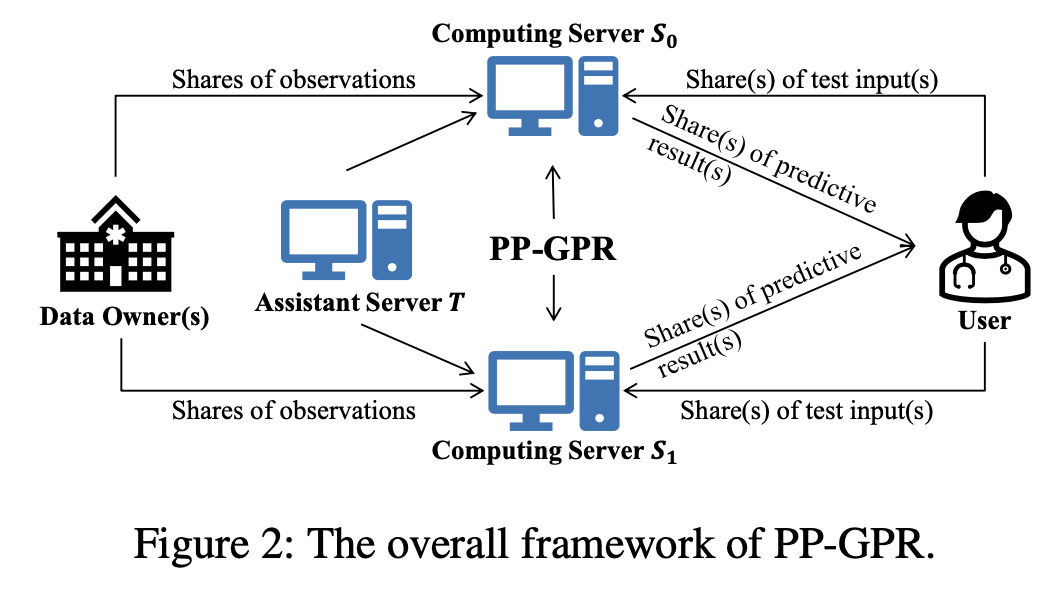
こちらの図をみるとやりたいことがとてもわかりやすいです。
ガウス回帰のおさらいのところで書いた様に、
学習データセットに対して、そしてテストデータに対して共分散行列を計算し、
行列席を取ることで、予測の平均値と分散について計算することができます。
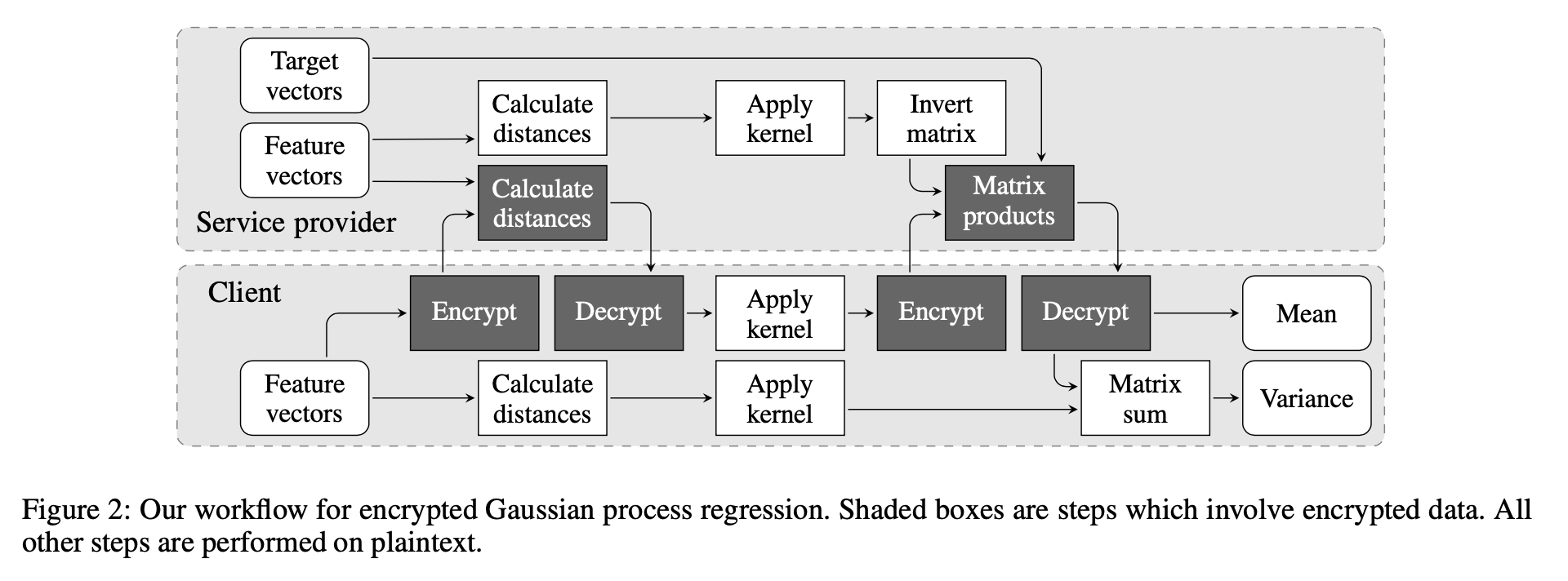
準同型暗号で計算する部分と、平文で計算する部分の切り分け
Service provider と書かれている部分は、準同型暗号を用いて暗号状態で計算されます。
また、Client と書かれている下の部分は暗号化、復号を実行し、必要な部分については平文で共分散行列を計算しています。
具体的には、テストデータ同士の共分散行列はクライアントサイドで計算してなんの問題もないため、平文でクライアントにそのまま計算してもらっています。
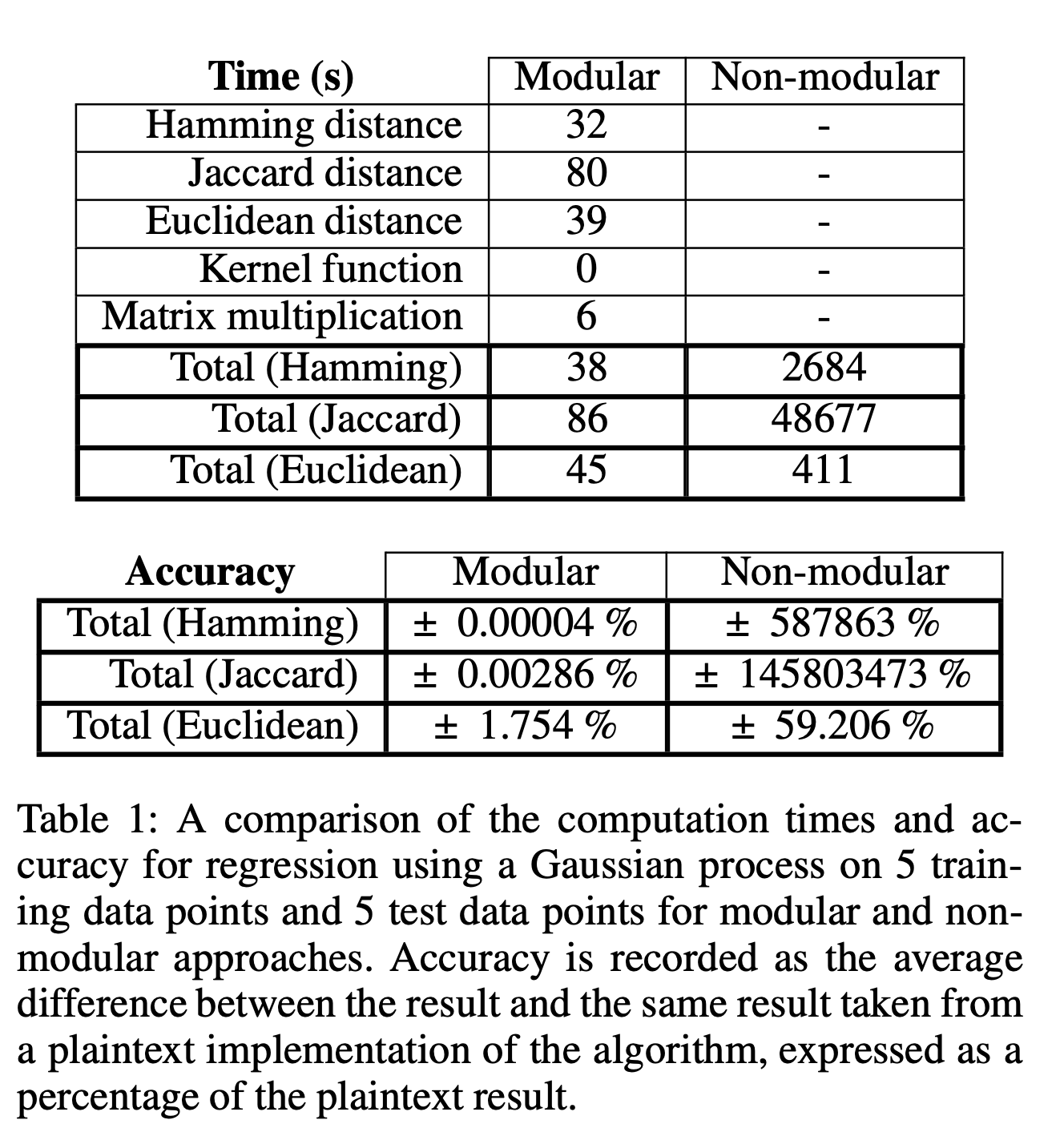
上のテーブルはガウス回帰に必要なモジュールの計算に要する時間です。
注意したいのは、学習データ、テストデータともに5件のみ使用しているということです(とても小さいデータセットであることに注意)
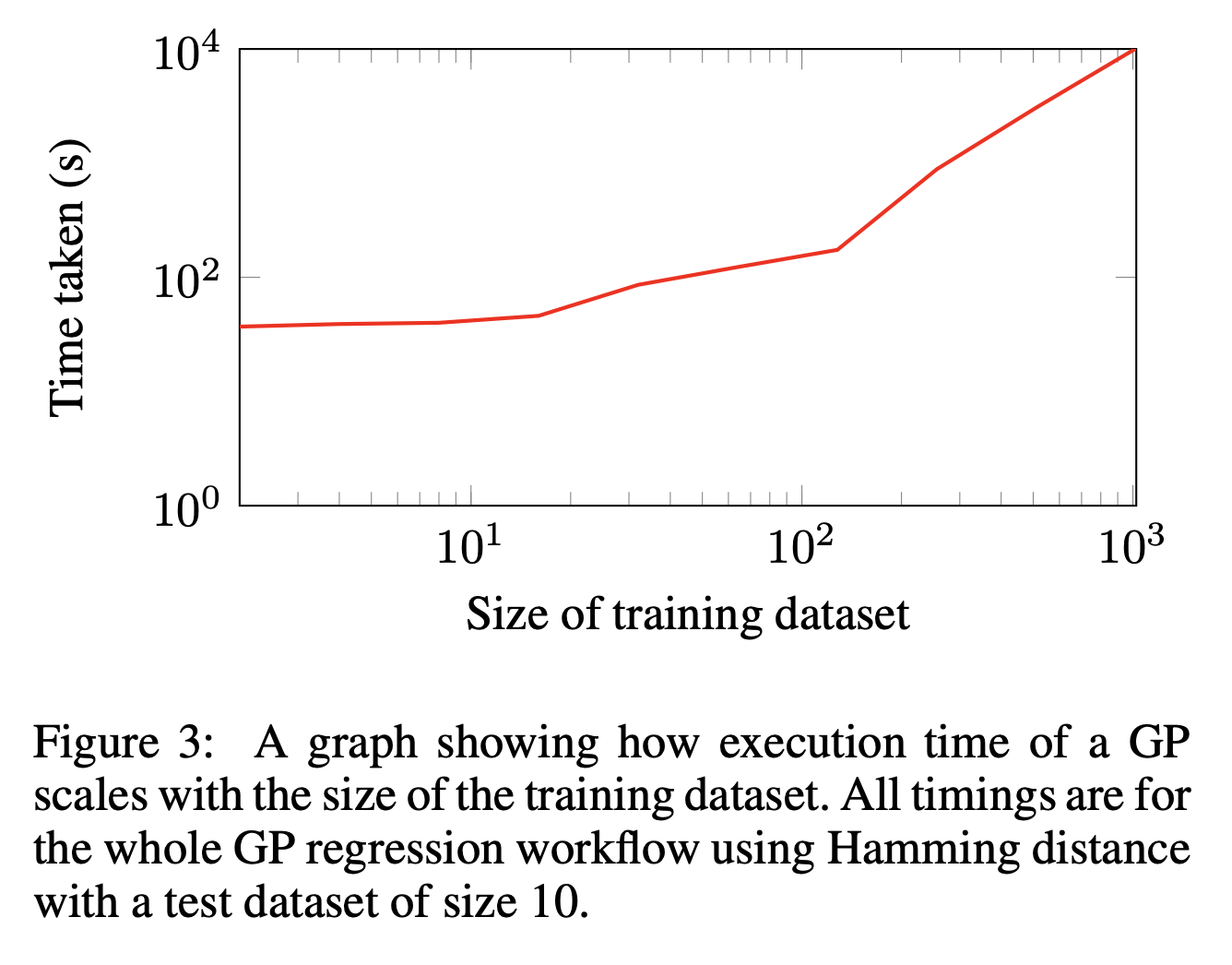
これは実際に回帰を計算する時のベンチマークとなっています。
横軸は学習データセットの数、テストデータセットは10個に対して推論を計算しています。
カーネルはハミング距離で計算されています。
Practical Privacy-Preserving Gaussian Process Regression via Secret Sharing
中国のHarbin Institute of Technology から2023年に発表された論文です。
秘密分散のアプローチをとっています。
アブストラクトから分かる様に、
シークレットシェアリングを利用してガウス過程回帰を学習、推論する実装とアルゴリズムの改善を行なった論文です。
改善された部分は主に、シークレットシェアリングを利用して計算することが難しいexp(x) の計算についてアルゴリズムの改善を行なったという点です。
SMPC(Secure Multi Party Computation) において、
ガウス過程回帰に必要な逆行列の計算や、Exp(x)の計算について、シークレットシェアリングを用いて高速に動作する様にアルゴリズムを改善することに注力しています。
第1章の最後に書かれている、この論文の主な貢献点についてです。
先ほど言及した様に、共分散行列、逆行列の計算を実装、
そして全体の学習について実験も含めて実測を行なっている点が高い貢献となっています。
2章ではシークレットシェアリングについておさらいが書かれています。
加算型の秘密分散方式のアプローチをとっており、足し算と掛け算についてはよく定式化されている通りです。
全体の構成とアルゴリズム
上のアルゴリズムが、ガウス過程回帰をシークレットシェアリングで計算するときの
全体の概要です。
Exp(x) を計算する時のアルゴリズム
Screenshot 2023-09-04 at 11.50.36.png
Cholesky Decompositionを利用した逆行列計算アルゴリズム
共分散行列のシェアの計算、
そしてそれらに対して行列積、逆行列を計算することで、
目的の回帰のシェアについて計算していることがわかります。
にも書かれている様に、Cholesky Decomposition は掛け算オーダーがO(n^3)のアルゴリズムです。
割り算オーダーはO(n^2)です。
Cholesky Decomposition を利用してから逆行列を計算することで、
計算式は加算、乗算、割り算で表されるため、今回の論文ではそれらをシークレットシェアリングでの実装に置き換えることで、
逆行列の計算を可能にしています。
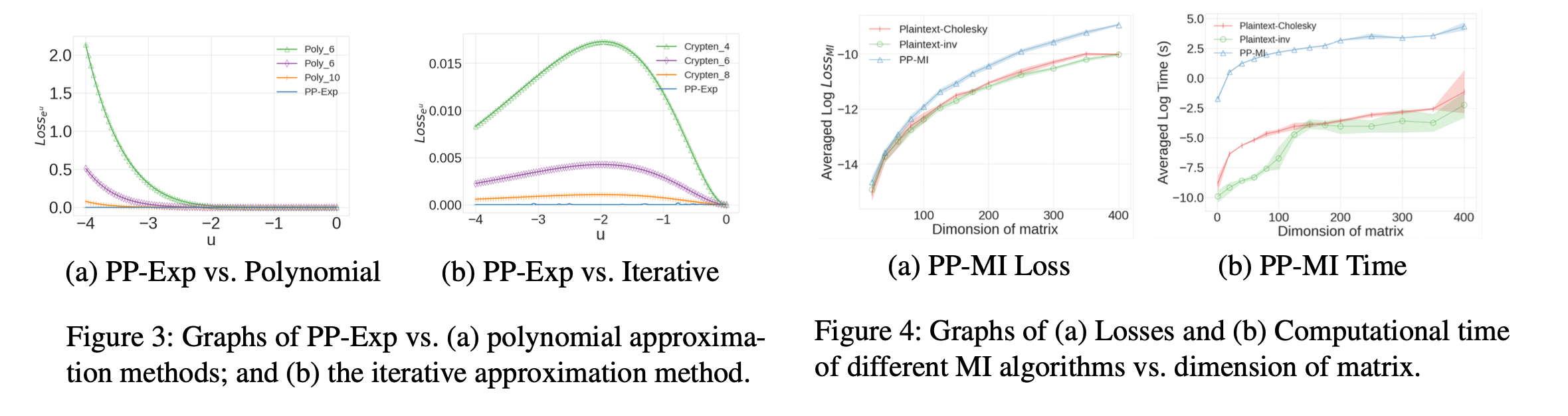
Exp(x)と逆行列計算の性能
上のグラフにまとめられている様に、論文のExp(x)のアルゴリズムは、
テイラー展開のような近似を用いたときに比べて誤差が小さく、
また、Crypten(Facebook Research によるSMPCの実装ライブラリ)
https://github.com/facebookresearch/CrypTen
に比べても非常に誤差が小さくなっているという結果になっています。
また、逆行列の計算についても、平文の実装に比べた誤差と速度結果についてまとめられています。!
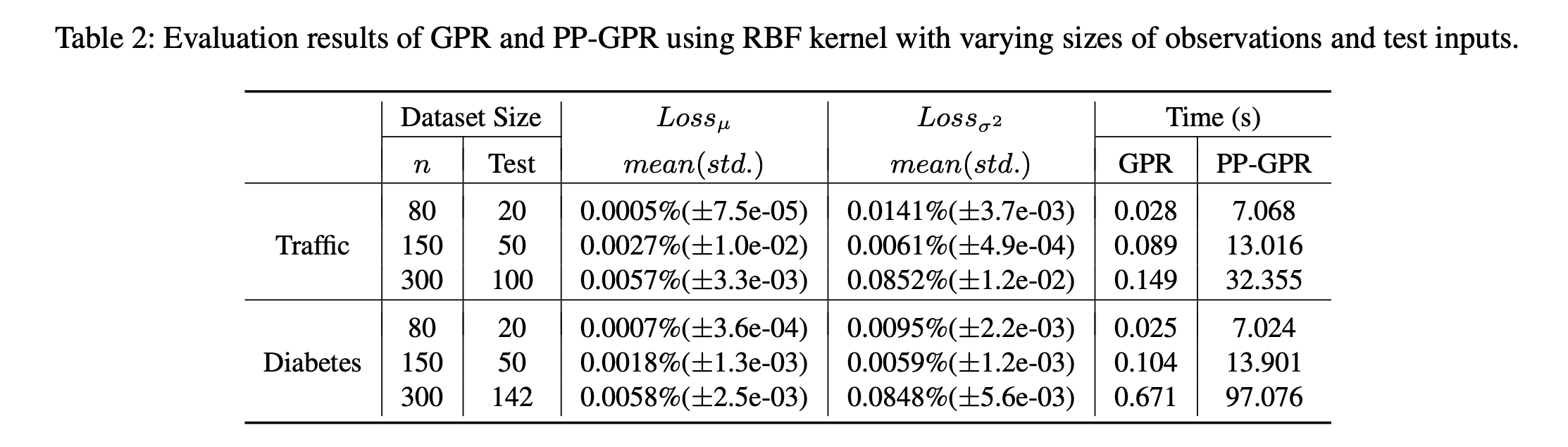
計測結果
2つのデータセットについて学習を行い、計算速度の実測を行なっています。
300件ほどの学習データ、100件のテストデータに対して、
推論が100秒ほどで完了していることがわかります。
まとめ
今回は、ガウス過程回帰を秘密計算を用いて実装している論文について、
- 準同型暗号を用いたアプローチ
- 秘密分散を用いたアプローチ
のそれぞれのかなり最近発表されたものについてみてみました。
ガウス過程回帰の計算は大きな共分散行列の計算と、
行列の逆行列計算に着地するということ、
それらを工夫して秘密計算でどう処理するか、というところのアルゴリズムの改善がどちらも行われていることについて理解していただけたかと思います。
中身の細かいところについては、論文を実際に読んでいただいて実装してみると理解が深まると思います。
今回はこの辺で。