こちらの記事は数理最適化 Advent Calender 2020 15日目の記事として書いたものです.
はじめに
本記事では数理最適化問題を解くため公開サーバーである NEOS Server [1] の概要およびその使い方について説明します.
NEOS Server とは
NEOS Server [1] とは様々な有償・無償の数理最適化ソルバーを搭載している公開サーバーです. ユーザは最適化問題を定義したファイル (モデルファイル) を Neos Server にアップロードすると, 指定したソルバーがサーバー上で解いた結果を取得することができます. モデルファイルをアップロードするため業務に関連する機密情報を含む最適化問題を解くのには使えませんが,人工的に作った問題例や先行研究で解かれている問題例を使ってソルバーのベンチマークをとるには便利です.
ちなみにかつて私の研究では会社でライセンスを取得していない有償ソルバーとの比較実験を行う必要があり Neos Server を使ってその実験結果をまとめたことがあります. 自身の環境で行った実験と Neos Server を使った実験では計算環境が異なるので厳密な比較ということにはなりませんが, 数値実験における参考値として Neos Server の結果を論文中に掲載できたことは当時大変助かりました.
以下, 具体的な最適化問題を例として NEOS Server を使って結果を得る一連の流れについて説明します.
NEOS Server の使い方手順
ここでは具体例として以下のような混合整数線形最適化問題 (出典元: [1]) を NEOS Server で解くことを考えます:
$$
\begin{align}
\text{maximize} \quad &4x_1 + 5x_2 \\
\text{subject to} \quad &2x_1 +2x_2 \leq 7\\
&3x_1 + 5x_2 \leq 14 \\
&x_1,x_2 \geq 0,\\
&x_1,x_2 :整数.
\end{align}
$$
1. ソルバーの選択
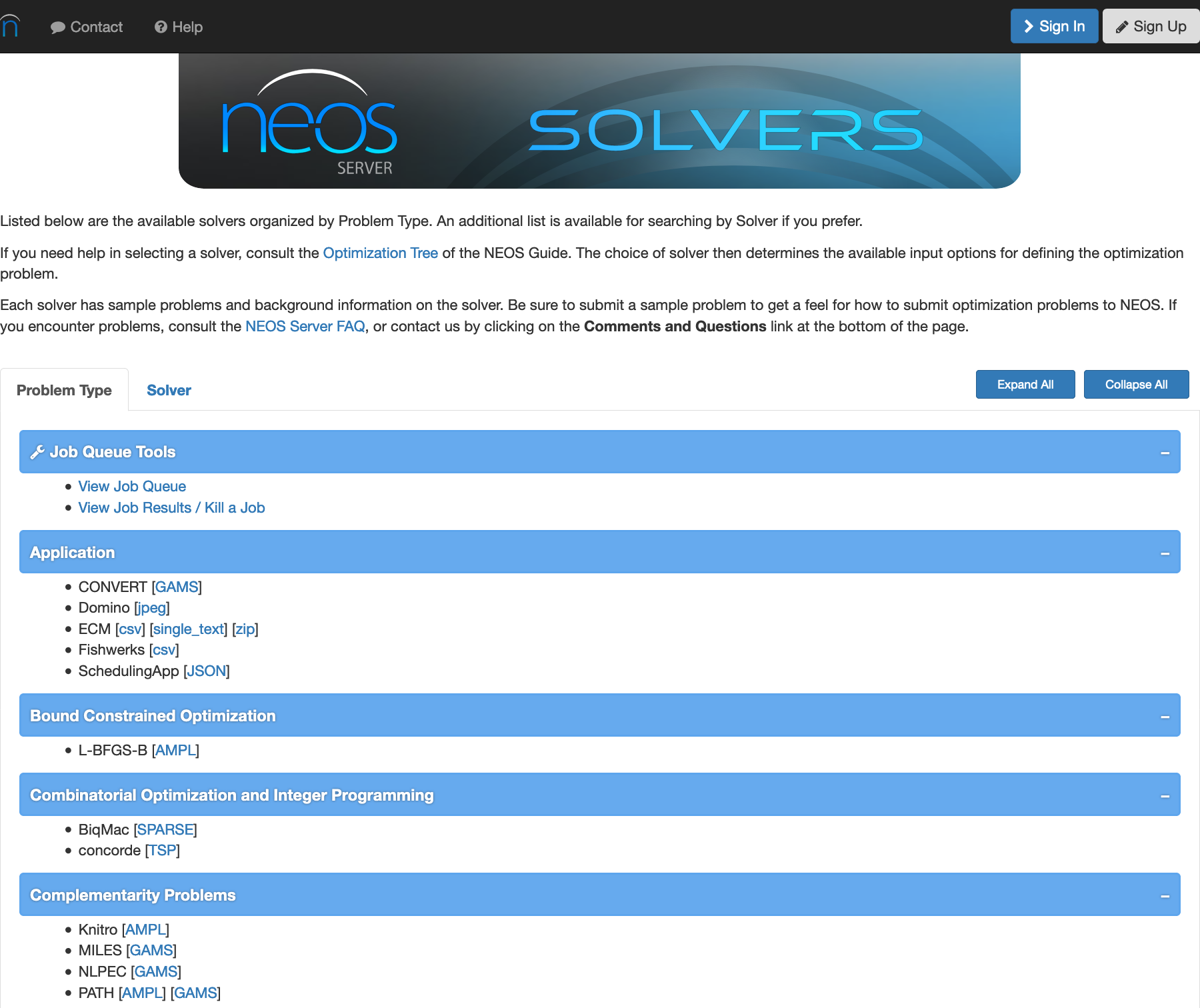
まずは最適化問題を解くためのソルバーを決めましょう.はじめに下記のページにアクセスしてみてください:
すると, このような画面が表示されます:
こちらのページでは NEOS サーバーで解くことが可能な最適化問題の種類およびそれぞれに適用可能なソルバーの一覧を見ることができます. 今回解こうと思っている問題は混合整数線形最適化問題なので, 上記のページ中 Mixed-integer Liner Programming の欄を見てみます. すると以下のような画面を見ることができます.
こちらの画面から, 混合整数線形最適化問題を解くためのソルバーとしては
- Cbc
- CPLEX
- feaspump などなど
が使用可能であることがわかります.
ではここでは例として有償の数理最適化ソルバー CPLEX を使って問題を解くこととしましょう. CPLEX の項目には
CPLEX [AMPL] [GAMS] [LP] [MPS] [NL]
と記載されています. ソルバーで数理最適化問題を解く際には, 最適化問題を定義するファイルを作成して入力する必要があります. ここで [AMPL Input][GAMS Input][LP Input]... と記されている部分はソルバー CPLEX の入力として使用できる入力のファイルの形式の種類を表しています.
最適化問題を定義するファイルの準備
さて, ここまでで CPLEX が使用できるファイル形式がわかりました. 続いて, このファイル形式に従って解きたい問題を具体的に記述しましょう. ここでは最適化問題を記述する代表的なフォーマットの一つである LP フォーマットで問題を記述してみます. 天下り的ですが先の混合整数線形最適化問題
$$
\begin{align}
\text{maximize} \quad &4x_1 + 5x_2 \\
\text{subject to} \quad &2x_1 +2x_2 \leq 7\\
&3x_1 + 5x_2 \leq 14 \\
&x_1,x_2 \geq 0,\\
&x_1,x_2 :整数.
\end{align}
$$
を LP フォーマットで記述すると以下のようになります (LP フォーマットの具体的な書き方については文献 [5] 参照):
maximize
4 x(1) + 5 x(2)
subject to
c1: 2 x(1) + 2 x(2) <= 7
c2: 3 x(1) + 5 x(2) <= 14
bounds
0 <= x(1)
0 <= x(2)
general
x(1) x(2)
end
定式化とLPファイルを見比べてみると, LP ファイルは比較的定式化の通り最適化問題を記述することができていることがわかるかと思います. このように記述したファイルを example.lp とでも適当にファイル名をつけて保存をしておきます.
Lpファイルを投入して解く
では実際に作成したLPファイルを NEOS Server にアップロードして CPLEX で解いてみましょう. 先ほどの
CPLEX [AMPL] [GAMS] [LP] [MPS] [NL]
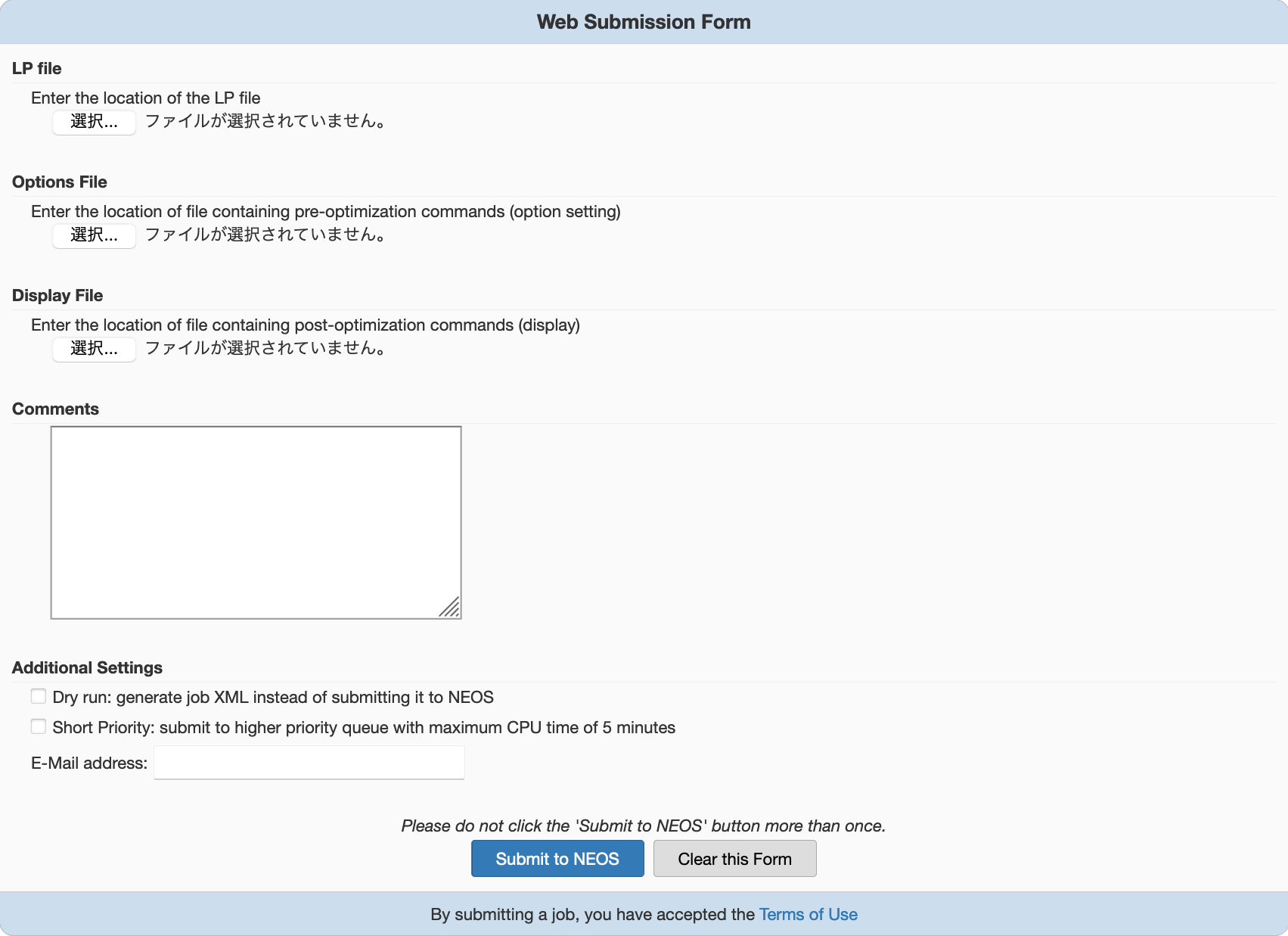
と表示されていた項目に関して, [LP] をクリックします. すると以下のようなモデルファイルをアップロードするページが表示されます.
こちらのページで, LP file の部分で先ほど作成した LP ファイルを選択してアップロードし, E-mail address の部分に自身の連絡先を入力します (連絡先の入力は必須ではありません). そして Submit to NEOS をクリックすると, NEOS Server 上にモデルファイルがアップロードされ CPLEX の計算が開始します.
結果の確認
NEOS Server 上の計算が終了すると, 以下のようなソルバーのログがブラウザ上で表示されます:
Executing on prod-exec-5.neos-server.org
Welcome to IBM(R) ILOG(R) CPLEX(R) Interactive Optimizer 12.7.0.0
with Simplex, Mixed Integer & Barrier Optimizers
5725-A06 5725-A29 5724-Y48 5724-Y49 5724-Y54 5724-Y55 5655-Y21
Copyright IBM Corp. 1988, 2016. All Rights Reserved.
Type 'help' for a list of available commands.
Type 'help' followed by a command name for more
information on commands.
CPLEX> New value for default parallel thread count: 4
CPLEX> Problem 'cplex.lp' read.
Read time = 0.00 sec. (0.00 ticks)
CPLEX> Found incumbent of value 0.000000 after 0.00 sec. (0.00 ticks)
Tried aggregator 1 time.
MIP Presolve modified 4 coefficients.
Reduced MIP has 2 rows, 2 columns, and 4 nonzeros.
Reduced MIP has 0 binaries, 2 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.00 sec. (0.00 ticks)
Tried aggregator 1 time.
MIP Presolve eliminated 2 rows and 2 columns.
All rows and columns eliminated.
Presolve time = 0.00 sec. (0.00 ticks)
Root node processing (before b&c):
Real time = 0.00 sec. (0.01 ticks)
Parallel b&c, 4 threads:
Real time = 0.00 sec. (0.00 ticks)
Sync time (average) = 0.00 sec.
Wait time (average) = 0.00 sec.
------------
Total (root+branch&cut) = 0.00 sec. (0.01 ticks)
Solution pool: 2 solutions saved.
MIP - Integer optimal solution: Objective = 1.4000000000e+01
Solution time = 0.00 sec. Iterations = 0 Nodes = 0
Deterministic time = 0.01 ticks (2.83 ticks/sec)
こちらのログでは,
MIP - Integer optimal solution: Objective = 1.4000000000e+01
となっているため, 先の最適化問題の最適値は 14 であることがわかります.
なおこのログの出力は LP ファイルアップロード時に指定した連絡先宛にも送られます. したがって NEOS Server の結果はブラウザを閉じてもメールであとから参照することができます.
おわりに: その他の参考情報
本記事では Neos Server を使うための必要最低限の方法について説明しました. 実際に Neos Server を使うためには事前に解きたい最適化問題を定式化してその問題をモデルファイルとして記述することが必要です. 例えば混合整数最適化問題に関する定式化に関しては文献 [2--4] が参考になります. また LP フォーマットの書き方, NEOS Server の使い方に言及している日本語の文献としては文献 [5] があり, またそのほかブログ記事による解説 [6] もあります.
参考文献
[1] NEOS Server: NEOS Server for Optimization. University of Wisconsin-Madison, 2020. https://www.neos-server.org/neos/
[2] 藤江哲也. 整数計画法による定式化入門. オペレーションズ・リサーチ 57.4 (2012): 190-197.
[3] 久保幹雄, J. P. ペドロソ, 村松正和,A. レイス: 新しい数理最適化 ~Python 言語と Gurobi で解く~. 近代科学社, 2012.
[4] 梅谷俊治. しっかり学ぶ最適化 モデリングからアルゴリズムまで. 講談社, 2020.
[5] 宮代隆平. 整数計画ソルバー入門. オペレーションズ・リサーチ,57-4 (2012),pp. 183-189.
[6] しまさん. NEOS Serverとは:難しいものはNEOS Serverに解かせよう. https://murabitoleg.com/neos/, 2020年12月14日閲覧 .