1. はじめに
ベイズ統計モデルは、自由度が高く線形混合モデルや階層モデル等、様々なモデリングが可能で、複雑なデータ解析等の応用が可能です。今回はベイズ統計の枠組みを使って、ちょっと複雑な実際の調査データ事例を使った解析をしてみたいと思います。
なお、ベイズ統計を使ったモデリング等について詳しくは、下記記事や馬場先生の「RとStanではじめる ベイズ統計モデリングによるデータ分析入門」を参考にしてください。(本投稿ではベイズ統計モデリングそのものには触れません) (2023.7.17更新)
2 . データ解析環境
-
Windows11 home
-
R version 4.2.3 & RStudio 2023.6.1 Build 524
※version 4.3.1では動きませんでした
-
'tidyverse' version 2.0.0
-
'rstan' version 2.26.21
-
'bayesplot' version 1.10.0
-
'loo' version 2.6.0
library(tidyverse)
library(tidybayes)
library(rstan)
library(bayesplot)
library(loo)
library(patchwork)
3 . DATAの概要
-
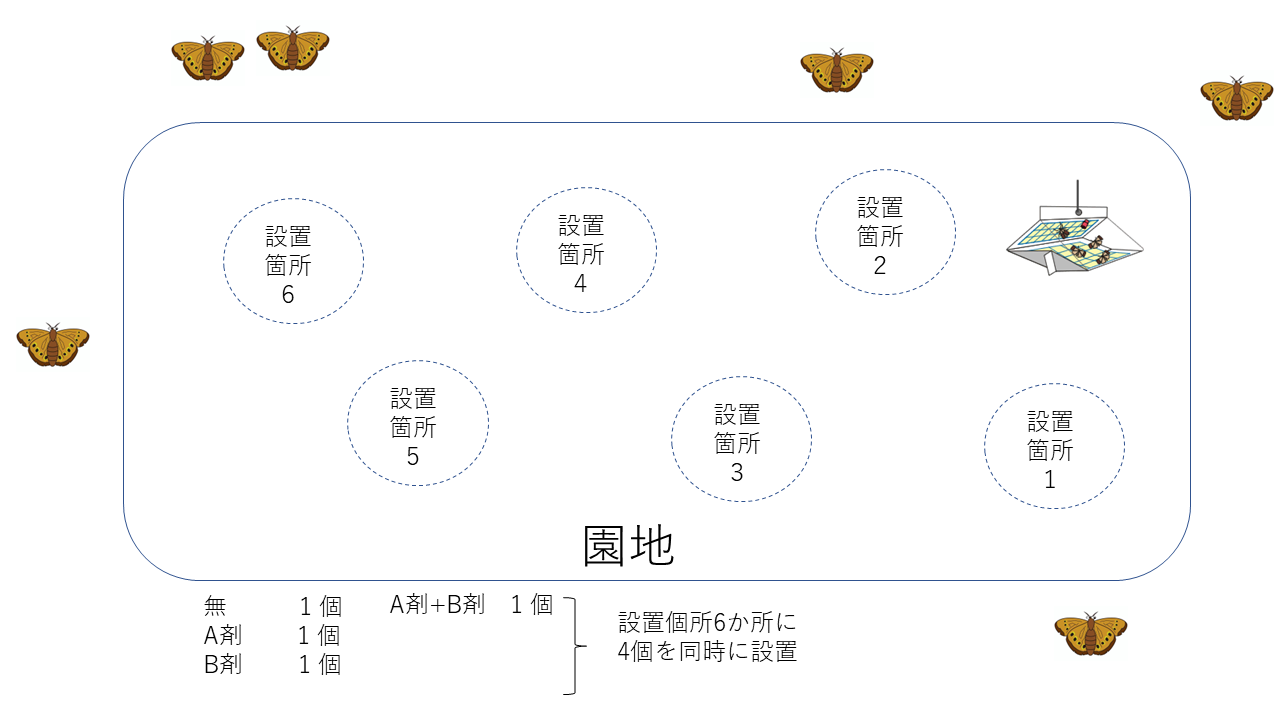
ここは、ある県のミカン園地
-
ミカンを害するM害虫に悩まされている
-
害虫を誘因させるトラップを使って誘殺したい
-
誘因する薬剤として既存のA剤に、新規のB剤が発売された
-
そこでトラップをしかけて、誘因薬剤の効果を試験することにした
-
試験区の概要
1.誘引剤なし(無)
2.A剤のみ
3.B剤のみ
4.A剤+B剤の混合
-
園地はA園地、B園地の2か所ある
-
1半旬(5日間)毎に試験区に誘殺された虫の数を調査した
-
害虫には発生時期があるので、発生前から終わりまで誘殺数を計時的に調査した
-
設置個所は、場所ごとの影響を少なくするために半旬毎に各試験区の設置個所を動かしながらローテーションした。
解析の目的は、新規薬剤であるB剤の効果があるかどうか?
(データは、実際に得られた実データを用いています)
rm(list = ls())
d = read.csv("https://raw.githubusercontent.com/kenkenvw/data/main/mikan_pest_insect.csv")
head(d,3)
> orchard location A.agent B.agent count time
> 1 A 2 0 0 0 1
> 2 A 3 1 0 0 1
> 3 A 4 0 1 0 1
orchard : 園地の情報
location : 設置個所 1-6
A.agent : 誘引剤Aの有無(0:無、1:有)
B.agent : 誘引剤Bの有無(0:無、1:有)
count : 誘殺数
time : 調査時期(半旬毎)1-10
g1 = ggplot(d, aes(x=time,y=count)) + geom_bar(stat = "identity") + theme_bw() + facet_grid(.~orchard) + xlab("園地の違い")+ylab("誘殺数")
# B剤との混合設置されていない条件
g2 = ggplot(d %>% filter(B.agent==0), aes(x=time,y=count)) + geom_bar(stat = "identity") + theme_bw() + facet_grid(.~A.agent) + xlab("A剤の効果")+ylab("誘殺数")
# A剤との混合設置されていない条件
g3 = ggplot(d %>% filter(A.agent==0), aes(x=time,y=count)) + geom_bar(stat = "identity") + theme_bw() + facet_grid(.~B.agent) + xlab("B剤の効果")+ylab("誘殺数")
g4 = ggplot(d, aes(x=time,y=count)) + geom_bar(stat = "identity") + theme_bw() + facet_grid(.~location) + xlab("設置個所の違い")+ylab("誘殺数")
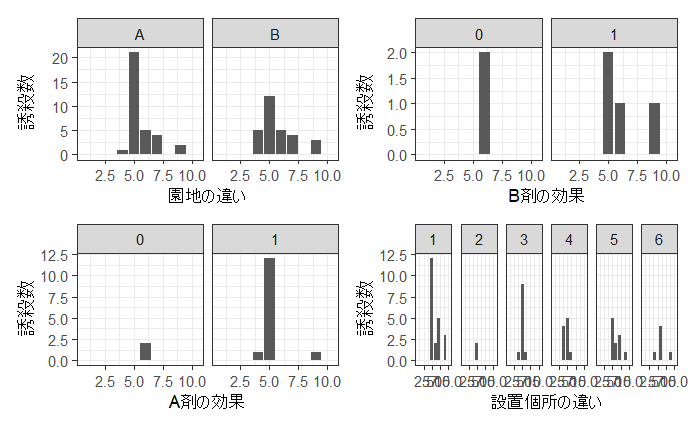
(g1/g2)|(g3/g4)
調査の結果、害虫の発生ピークは 5timeの時期で、時期だけでなく設置個所による発生量もそれぞれ異なっているようです。薬剤のA剤は誘因効果はありそうだが、B剤の効果はあるかもしれないぐらい?
4 . 統計モデリングを使った解析
4 . 1 ベイズGLMによる解析
最初に、誤差項にポアソン分布を指定するGLMを使ったベイズ推定をしてみます。 事前分布は特に指定しない(無情報事前分布)を使います。
以下のstanファイルをtestA.stanとして作成します。
// ポアソン回帰モデル
data {
int<lower=0> N;//data数
int<lower=0> x1[N];// A.agentの有無
int<lower=0> x2[N];// B.agentの有無
int<lower=0> x3[N];// 園地の違い
int<lower=0> Y[N];//トラップに誘殺された数
}
parameters {
real beta0;//切片
real beta1;//A.agentの回帰係数
real beta2;//B.agentの回帰係数
real beta3;//園地の回帰係数
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i] = exp(beta0 + beta1*x1[i] + beta2*x2[i] + beta3*x3[i]);
}
model {
for(i in 1:N)
Y[i] ~ poisson(lambda[i]);
}
generated quantities {
vector[N] log_lik;
for (i in 1:N)
//対数尤度を計算(WAIC)
log_lik[i] = poisson_lcdf(Y[i] | lambda[i] );
}
モデリングは次のとおりになります。
Y \sim poisson(exp(\beta_0 +\beta_1x_1+\beta_2x_2+\beta_3x_3 ))
$Y$ : 誘殺数
$β_0$:切片
$β_1$:A.agentの偏回帰係数
$β_2$:B.agentの偏回帰係数
$β_3$:園地の偏回帰係数
誘殺数がポアソン分布によって得られると仮定し、3個の説明変数によってモデリングを行います。
また、WAIC(情報量基準)を計算するため、generated quantities{}で対数尤度を計算してます。
次のRコードでstanモデルを動かします。
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())
set.seed(123)
data = compose_data(N=nrow(d),
x1=d$A.agent,
x2=d$B.agent,
x3=d$orchard,
Y=d$count)
fitA = stan(file ="model/testA.stan",data=data)
収束しているかどうかrhatをチェックします。rhatが1.05を目安にします。
sum(rhat(fitA)>1.05)
>[1] 0
無事に収束しているようです。
$β_1$:A.agentと$β_2$:B.agentの偏回帰係数の事後分布を見て効果を推定します。
plot_title = ggtitle("Posterior distributions",
"with medians and 95% intervals")
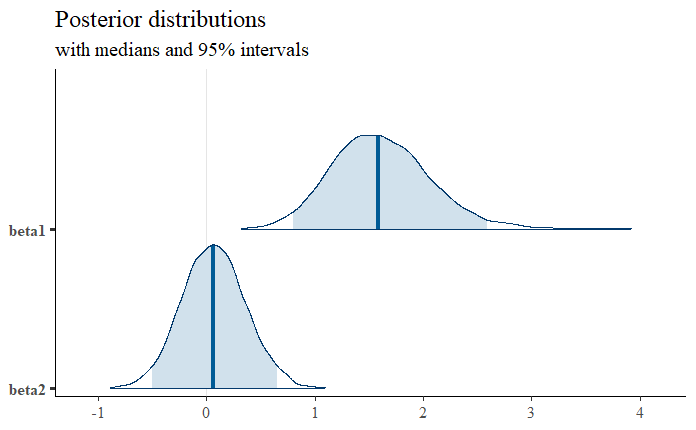
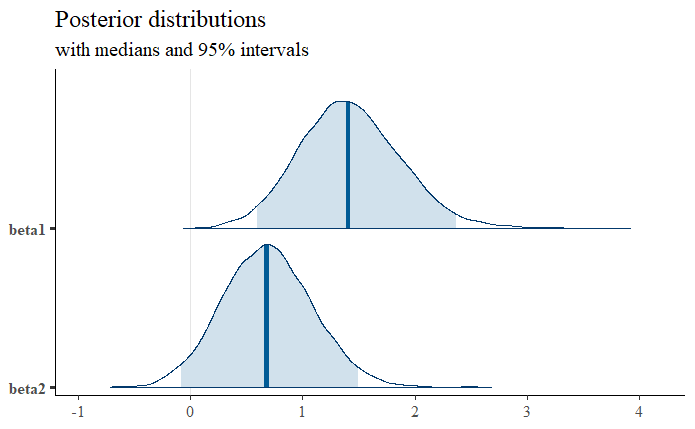
mcmc_areas(fitA,
pars = c("beta1","beta2"),
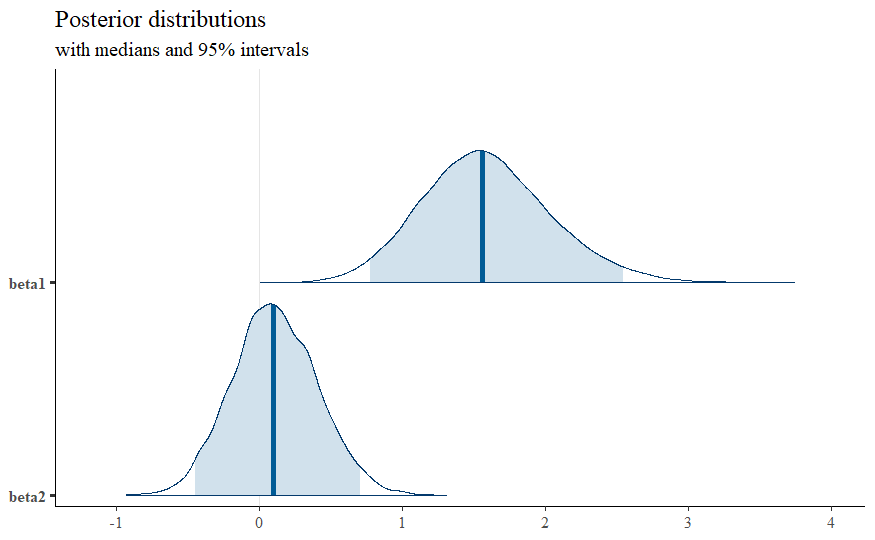
prob = 0.95) + plot_title
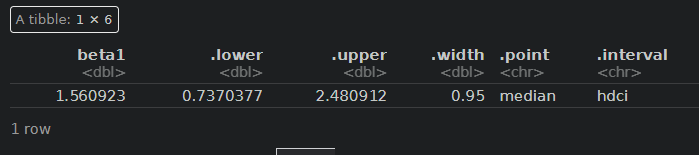
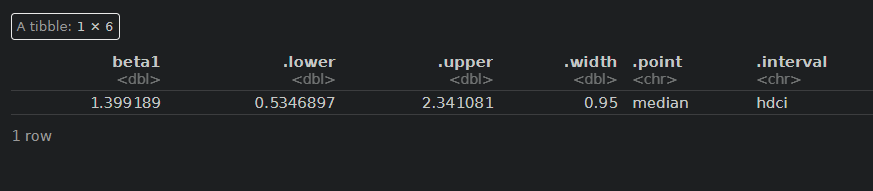
fitA %>% spread_draws(beta1) %>% median_hdci()
fitA %>% spread_draws(beta2) %>% median_hdci()
A剤(beta1)は、1.5付近をピークに95%信用区間には0を含まないため、効果は統計的にも有意にありそうですが、B剤(beta2)は効果は0に近く分布しており、とても効果があるとは言えなさそうです。
looパッケージを使ってWAICを推定します。
WAICとはWidely Applicable information criterion (Watanabe, 2010)の略でベイジアンモデルで用いられる情報量基準の1つで、model選択に使います。従来の統計学で用いられるAICと等価になります。
tmp = extract_log_lik(fitA)
WAIC_A = waic(tmp)
WAIC_A$estimates
> Estimate SE
>elpd_waic -48.709045 3.3157087
>p_waic 1.656564 0.1336712
>waic 97.418090 6.6314173
WAICは97.4となりました。
4 . 2 ベイズGLMMによる解析: 設置場所の違い
しかし、6か所の設置場所毎に害虫の発生量が異なっているので、その影響が考えられます。設置個所毎にランダム効果を考えてみます(GLMMモデルになります)。
以下のstanファイルをtestB.stanとして作成します。
// GLMMモデル 設置場所の違いをランダム効果とする
data {
int<lower=0> N;//data数
int<lower=0> x1[N];//A.agentの有無
int<lower=0> x2[N];//B.agentの有無
int<lower=0> x3[N];//園地の違い
int<lower=0> Y[N]; //トラップに誘殺された数
int loc[N];//設置場所
}
parameters {
real beta0;//切片
real beta1;//A.agentの回帰係数
real beta2;//B.agentの回帰係数
real beta3;//園地の回帰係数
real betaloc[6];//設置場所の回帰係数(ランダム効果)
real<lower=0> loc_sigma;//設置場所の標準偏差(ランダム効果)
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i] = exp(beta0 + beta1*x1[i] + beta2*x2[i] + beta3*x3[i] + betaloc[loc[i]] );
}
model {
for(i in 1:N)
Y[i] ~ poisson(lambda[i]);
for(i in 1:6){
betaloc[i] ~ normal(0,loc_sigma);//ランダム効果
}
}
generated quantities {
vector[N] log_lik;
for (i in 1:N)
log_lik[i] = poisson_lcdf(Y[i] | lambda[i] );
}
先ほどのtestAとの違いは設置個所毎に新たに6か所のbetaloc[6]のパラメータを入れて、
betaloc[i] ~ normal(0 , loc_sigma);
と平均0、共通の標準偏差(loc_sigma)を持つ正規分布に従う効果を指定します。このことで、設置個所毎のグループ効果を考慮するポアソン分布と正規分布の混合分布モデルになります。
早速testBをキックします。
set.seed(123)
data=compose_data(N=nrow(d),
x1=d$A.agent,
x2=d$B.agent,
x3=d$orchard,
loc=d$location,
Y=d$count)
fitB = stan(file ="model/testB.stan",data=data)
sum(rhat(fitB)>1.05)
>[1] 0
収束しているようなので、testAと同様にパラメータの事後分布を見てみます。
plot_title = ggtitle("Posterior distributions",
"with medians and 95% intervals")
mcmc_areas(fitB,
pars = c("beta1","beta2"),
prob = 0.95) + plot_title
fitB %>% spread_draws(beta1) %>% median_hdci()
fitB %>% spread_draws(beta2) %>% median_hdci()
どうやらmodelAと同様にB剤の効果は設置場所の違いを考慮しても効果は見られないようです。
やはり効果はないのでしょうか?
WAICを計算します。
tmp = extract_log_lik(fitB)
WAIC_B = waic(tmp)
WAIC_B$estimates
> Estimate SE
>elpd_waic -46.913386 4.1164308
>p_waic 3.695031 0.3842699
>waic 93.826771 8.2328615
WAICは93.8とtetsAの97.4よりモデルの選択性は少し良くなりました(小さい方が良い)
4 . 3 ベイズGLMMによる解析: 設置場所の違い+相互作用項
設置個所の違いをランダム効果としたまま、B剤の効果は単独ではなくてもA剤との相互作用による効果がある可能性を調べてみます。
交互作用モデルをtestAB.stanとします。
// GLMMモデル +設置場所(ランダム効果)+相互作用項
data {
int<lower=0> N;//data数
int<lower=0> x1[N];//A.agentの有無
int<lower=0> x2[N];//B.agentの有無
int<lower=0> x3[N];//園地の違い
int<lower=0> Y[N];//トラップに誘殺された数
int loc[N]; //設置場所
}
parameters {
real beta0;//切片
real beta1;//A.agentの回帰係数
real beta2;//B.agentの回帰係数
real beta3;//園地の回帰係数
real beta4;//A.agentとB.agentの相互作用項
real betaloc[6];//設置場所の回帰係数(ランダム効果)
real<lower=0> loc_sigma;//設置場所の標準偏差(ランダム効果)
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i]= exp(beta0 + beta1*x1[i] + beta2*x2[i] + beta3*x3[i] + beta4*x1[i]*x2[i] + betaloc[loc[i]]);
}
model {
for(i in 1:N)
Y[i] ~ poisson(lambda[i]);
for(i in 1:6)
betaloc[i] ~ normal(0,loc_sigma);//ランダム効果
}
generated quantities {
vector[N] log_lik;
for (i in 1:N)
log_lik[i] = poisson_lcdf(Y[i] | lambda[i] );
}
キックします。
set.seed(123)
data = compose_data(N=nrow(d),
x1=d$A.agent,
x2=d$B.agent,
x3=d$orchard,
loc=d$location,
Y=d$count)
fitAB = stan(file ="model/testAB.stan",data=data)
sum(rhat(fitAB)>1.05)
>[1] 0
収束しているようなので、今までと同様にパラメータの事後分布を見てみます。
plot_title = ggtitle("Posterior distributions",
"with medians and 95% intervals")
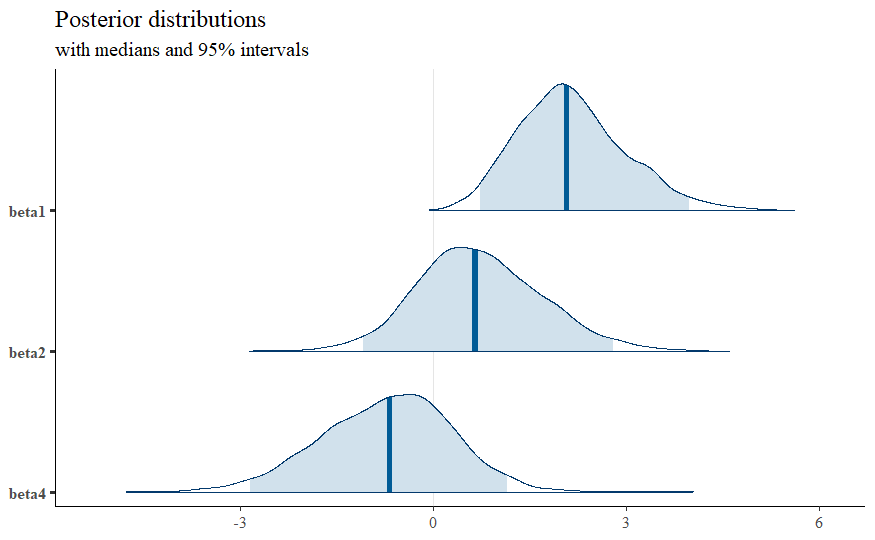
mcmc_areas(fitAB,
pars = c("beta1","beta2","beta4"),
prob = 0.95) + plot_title
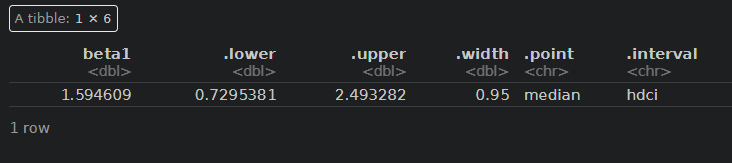
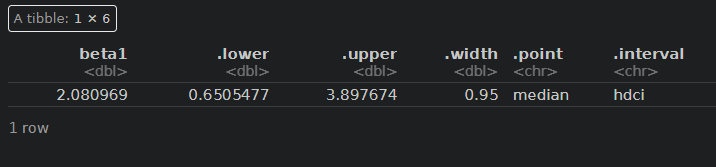
fitAB %>% spread_draws(beta1) %>% median_hdci()
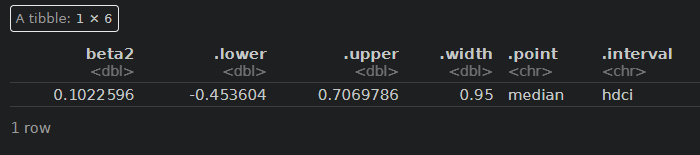
fitAB %>% spread_draws(beta2) %>% median_hdci()
fitAB %>% spread_draws(beta4) %>% median_hdci()
A剤
B剤
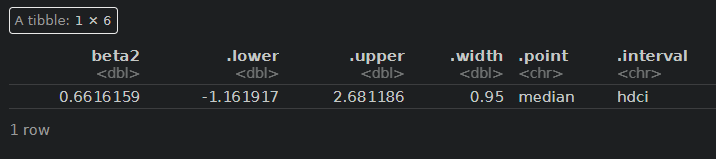
A剤とB剤の交互作用
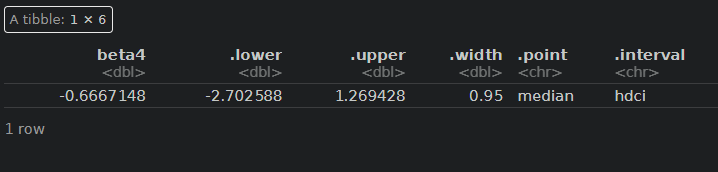
相互作用項を考慮すると、B剤の効果がやや上がりました(0.1→0.7)。ただし、0を下回る範囲も大きいため、効果の不確実性は高いです。
またA剤とB剤の相互作用の関係は-0.7となっていますが、やはり信用区間に0を含む範囲も大きいため、相互作用はあまりないと思われます。
tmp <- extract_log_lik(fitAB)
WAIC_AB <- waic(tmp)
WAIC_AB$estimates
> Estimate SE
>elpd_waic -47.074555 4.0839451
>p_waic 3.960273 0.3893603
>waic 94.149110 8.1678903
WAICは94.1とtestBの93.8とほぼ同じです。
4 . 4 ベイズGLMMによる解析 設置場所の違い + 時点の違い
データを良く見てみると、どうやら設置場所だけでなく時点によっても害虫の発生量は異なっています。5time時点をピークに発生量は増加・減少する傾向があります。
そこで、GLMMモデルに時点の違いをランラム効果として追加します。
以下のstanファイルをtestC.stanとして作成します。
// GLMMモデル +設置場所(ランダム効果)+時点(ランダム効果)
data {
int<lower=0> N;//data数
int<lower=0> x1[N];//A.agentの有無
int<lower=0> x2[N];//B.agentの有無
int<lower=0> x3[N];//園地の違い
int<lower=0> Y[N];//トラップに誘殺された数
int loc[N];//設置場所
int jiten[N];//設置場所
}
parameters {
real beta0;//切片
real beta1;//A.agentの回帰係数
real beta2;//B.agentの回帰係数
real beta3;//園地の回帰係数
real betaloc[6];//設置場所の回帰係数(ランダム効果)
real<lower=0> loc_sigma;//設置場所の標準偏差(ランダム効果)
real betajten[10];//時点毎の回帰係数(ランダム効果)
real<lower=0> jten_sigma;//時点毎の標準偏差(ランダム効果)
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i] = exp(beta0 + beta1*x1[i] + beta2*x2[i] + beta3*x3[i] +betajten[jiten[i]] + betaloc[loc[i]] );
}
model {
for(i in 1:N)
Y[i] ~ poisson(lambda[i]);
for(i in 1:10)
betajten[i] ~ normal(0, jten_sigma);
for(i in 1:6)
betaloc[i] ~ normal(0, loc_sigma);
}
generated quantities {
vector[N] log_lik;
for (i in 1:N)
log_lik[i] = poisson_lcdf(Y[i] | lambda[i] );
}
先ほどのtestBとの違いは、1-10timeの時点毎にbetajten[10]のパラメータを追加し、場所毎の違いと同様に、
betajten[i] ~ normal(0, jten_sigma);
と平均0と共通の標準偏差(jten_sigma)を持つ正規分布に従うと指定しています。2つのランダム効果を持つ少し複雑なモデルになっています。
早速modelCをキックします。
set.seed(123)
data=compose_data(N=nrow(d),
x1=d$A.agent,
x2=d$B.agent,
x3=d$orchard,
loc=d$location,
jiten=d$time ,
Y=d$count)
fitC = stan(file ="model/testC.stan",data=data,iter = 9000,warmup = 4500,thin = 3)
MCMCはデフォルトの設定だと有効サンプル数(ESS)が低すぎると警告がでたため、thinの設定を3とし、iterを9000としたら、警告は出なくなりました。
sum(rhat(fitC)>1.05)
>[1] 0
収束には問題はなさそうなので、modelBと同様にパラメータの事後分布を見てみます。
plot_title = ggtitle("Posterior distributions",
"with medians and 95% intervals")
mcmc_areas(fitC,
pars = c("beta1","beta2"),
prob = 0.95) + plot_title
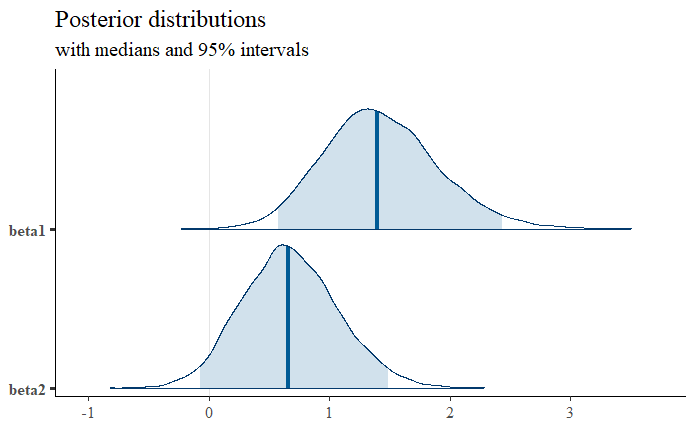
設置場所と時点の違いをランダム効果に指定することで、初めてB剤の効果がありそうな結果が出てきました。
fitC %>% spread_draws(beta1) %>% median_hdci()
fitC %>% spread_draws(beta2) %>% median_hdci()
B剤

testCではB剤の95%信用区間の下限値もわずかに(-0.03)、0を下回っているだけなので、ほぼ効果はあるとみてよいと思います。
次にWAICを見てみます。
tmp <- extract_log_lik(fitC)
WAIC_C <- waic(tmp)
WAIC_C$estimates
>警告:
>3 (2.5%) p_waic estimates greater than 0.4. We recommend trying loo instead. >Estimate SE
>elpd_waic -28.678246 5.148631
>p_waic 6.315101 1.500210
>waic 57.356491 10.297262
waicの標準誤差が少し大きくなっていますが、testCは57.4とtestBの94.1よりも大幅によくなっています。
モデルの選択性も向上し、この結果の方が妥当と考えてもよいため、B剤は、統計的に有意とまではいかないものの、効果は期待できそうです。
4 . 5 ベイズGLMMによる解析 設置場所の違い + 時点の違いに自己相関モデルを入れる
ここでtestCでは時点毎に独立を仮定したランダム効果を指定しましたが、通常、害虫の発生消長は一つ前の時点の影響を受けるため(一つ前の時点の発生数と自己相関する)独立するとは言えないので、この時点の影響の自己相関関係をモデルに入れてみます。
以下のstanファイルをtestD.stanとして作成します。
// GLMMモデル 設置場所の違い + 時点について自己相関を組み込む
data {
int<lower=0> N;//data数
int<lower=0> x1[N];//A.agentの有無
int<lower=0> x2[N];//B.agentの有無
int<lower=0> x3[N];//園地の違い
int<lower=0> Y[N];//トラップに誘殺された数
int loc[N]; //設置場所
int jiten[N];//設置場所
}
parameters {
real beta0;//切片
real beta1;//A.agentの回帰係数
real beta2;//B.agentの回帰係数
real beta3;//園地の回帰係数
real betaloc[6];//設置場所の回帰係数(ランダム効果)
real<lower=0> loc_sigma;//設置場所の標準偏差(ランダム効果)
real betajten[10];//時点毎の回帰係数(ランダム効果)
real<lower=0> jten_sigma;//時点毎の標準偏差(ランダム効果)
}
transformed parameters{
real lambda[N];
for(i in 1:N)
lambda[i]=exp(beta0 + beta1*x1[i] + beta2*x2[i] + beta3*x3[i] +betajten[jiten[i]] + betaloc[loc[i]] );
}
model {
betajten[1] ~ normal(0, jten_sigma);
for(i in 1:N)
Y[i] ~ poisson(lambda[i]);
for(i in 2:10)//自己相関モデル
betajten[i] ~ normal(betajten[i-1], jten_sigma);
for(i in 1:6)
betaloc[i] ~ normal(0, loc_sigma);
}
generated quantities {
vector[N] log_lik;
for (i in 1:N)
log_lik[i] = poisson_lcdf(Y[i] | lambda[i] );
}
testCとの違いは、最初の時点は、betajten[1] ~ normal(0, jten_sigma)と平均0の正規分布に従いますが、次の時点からは、
for(i in 2:10){
betajten[i] ~ normal(betajten[i-1], jten_sigma); //自己相関モデル
}
一つ前の時点の平均に従います。つまり、自己相関関係がモデリングされます。
早速、RでtestDをキックします。
set.seed(123)
data=compose_data(N=nrow(d),
x1=d$A.agent,
x2=d$B.agent,
x3=d$orchard,
loc=d$location,
jiten=d$time ,
Y=d$count)
fitD = stan(file ="model/testD.stan",data=data,iter = 9000,warmup = 4500,thin = 3)
>警告: There were 90 transitions after warmup that exceeded the maximum treedepth. >Increase max_treedepth above 10. See
>https://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded 警告: Examine the >pairs() plot to diagnose sampling problems
モデルが複雑になってきた影響なのか、アラートが出始めました。
事後サンプリングのうち90個が最大treedepthに達したようですが、これはstanが用いているNo-U-Turn-Samplerの効率の問題のようですので、この警告は無視しても問題はなさそうです。
sum(rhat(fitD)>1.05)
>[1] 0
収束性も問題はなさそうです。
plot_title = ggtitle("Posterior distributions",
"with medians and 95% intervals")
mcmc_areas(fitD,
pars = c("beta1","beta2"),
prob = 0.95) + plot_title
tmp <- extract_log_lik(fitD)
WAIC_D <- waic(tmp)
WAIC_D$estimates
>警告:
>3 (2.5%) p_waic estimates greater than 0.4. We recommend trying loo instead. > > Estimate SE
>elpd_waic -28.567226 5.103247
>p_waic 6.211752 1.479079
>waic 57.134452 10.206495
testDのWAICは57.1でtestCのWAIC57.4とほぼ同等になりました。
モデルの選択性としては、どちらのモデルも変わりはないことになります。
係数を比較してみまず
fitD %>% spread_draws(beta1) %>% median_hdci()
fitD %>% spread_draws(beta2) %>% median_hdci()
testCとほぼほぼ同じ結果になりました。
A剤1.40、B剤0.66~0.68とほぼ同じでした。時点の自己相関関係をモデルに入れても、その効果はそれほど強くなく、この仮定があってもなくても結果はほぼ変わりませんでした。
結論としてB剤の効果はありそうだと言えます。
5. まとめ
時点と場所差の違いを混合モデルとすることで、B剤の効果が明らかになった。また、A剤とB剤の相互作用による効果はあまりない。A剤の偏回帰係数1.4で、exp(1.4):約4倍の効果が見込まれる。B剤の偏回帰係数は0.7で,exp(0.7):約2倍の効果が見込まれる。ただし、B剤の95%信用区間に0を含むため、いわゆる統計的に有意ではないが、効果はある可能性が高い。(90%信用区間では0が含まれない)
いかがでしたでしょうか。このようにベイズ統計モデリングはデータ構造を見ながら、その都度、モデルを自由に改変できるため、自由度が非常に高いのが特徴です。
6. 参考
(Web)
線形混合モデルと階層ベイズモデルを使ったデータ解析の実践
(書籍)

実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門
[KS情報科学専門書]