1.モチベーション
介入措置が事前に割り当てられている実験データでなくアンケート調査みたいな観察データでも、分析と称して、相関関係がないと因果関係がない(例えば事業効果分析であれば、事業効果が見られなかったなど)の単純な分析をする事例が見られる。
こうした分析は時には社会的に大きな影響を与えているので、特に相関が見られなかったから効果がなかった(因果関係があれば必ず相関関係があるという思い込み)という分析事例について、シミュレーションデータで検証する。
また、因果関係の推定するための統計的因果推論の手法の一つである操作変数法をベイズ推定を使ってやってみたい。
2.シミュレーションDATA
使用するライブラリと環境
library(tidyverse)
library(rstan)
library(ggdag)
theme_set(theme_dag())
以下の環境で解析した
R version 4.2.3 (2023-03-15 ucrt) -- "Shortstop Beagle"
RStudio 2024.04.2 Build 764
OS:Windoes11
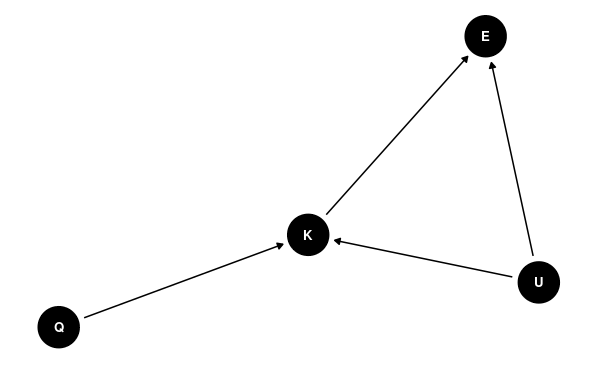
始めにシミュレーションデータを設定する。n=500人、K, E, Qというある個人iの能力を図る指標を設定する。
EとK連続値の指標である。
Qはカテゴリー指数で4つのカテゴリー{1,2,3,4}を持つ
Kは、因果関係としてQの影響を受ける。Uは、ここでは未観測の交絡要因である。
K_i \sim U_i + Q_i
EはKに影響を受けるが、未観測の交絡要因Uが負の影響を大きく与えている。
E_i \sim 0.5 K_i-1.5U_i
真の因果関係は、EはKが1単位増えるごとに0.5単位増加する影響を与えている。
dagify(
K ~ U,
E ~ K,
E ~ U,
K ~ Q
) %>%
ggdag()
UはEとKに影響を与える共変量であり、バックドアパスとも呼ばれる。Uは未知の要因であり、関心はKとEとの間に因果関係があるかどうかである。
シミュレーションデータを作成する。データは正規化して解析する。
rm(list=ls())
set.seed(123456)
N = 500
U = rnorm( N)
Q = sample( 1:4 , size=N , replace=TRUE )
K = rnorm( N , U + Q )
E = rnorm( N , 0.5*K - 1.5*U )
dat_list = list(
E=scale(E) ,
K=scale(K) ,
Q=scale(Q) ,
U=scale(U))
dat = as.data.frame(dat_list)
3.相関と回帰分析
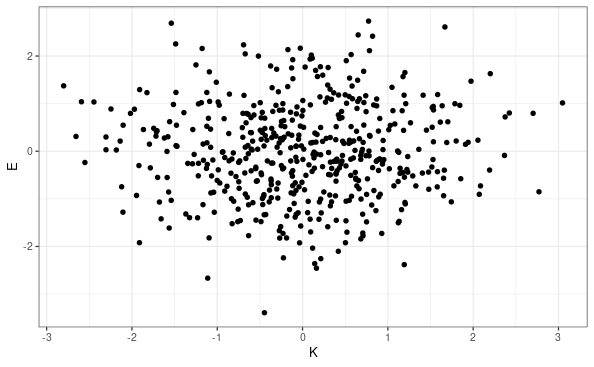
まず散布図をプロットする
ggplot(dat,aes(x=K,y=E)) + geom_point()+theme_bw()
cov(dat$K, dat$E)
[1] 0.02149292
相関係数は限りなく0に近い。
単回帰分析をしてみると・・
fit1 = lm(E ~ K, data=dat)
summary(fit1)
Call:
lm(formula = E ~ K, data = dat)
Residuals:
Min 1Q Median 3Q Max
-3.3821 -0.6597 -0.0200 0.6979 2.7225
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.145e-17 4.476e-02 0.00 1.000
K 2.149e-02 4.480e-02 0.48 0.632
Residual standard error: 1.001 on 498 degrees of freedom
Multiple R-squared: 0.0004619, Adjusted R-squared: -0.001545
F-statistic: 0.2302 on 1 and 498 DF, p-value: 0.6316
Kの係数は、0.02(単回帰だから相関係数と一致する)であり、そのp値は0.632になった。係数に有意差はなく、KはEに影響を与えない。
相関は全く見られず、係数も有意ではない。この散布図だけを見ると、Kが向上してもEには影響を与えないという結論をだすかもしれない。
このようなバイアスが生じている原因は、上記の場合、未観測の交絡要因であるUの分布が偏ることによる影響がマイナスに働いているためであり、これは選択バイアスなどから生じることが多い。
データの各要因をランダム化して割り付けることができれば(RCT化)、未観測の交絡要因による影響の分布がバランシングされるため、その影響をほぼ0とすることが可能であるが、実験データでなく観察データでは難しいことが多い。
もし未観測のU要因が観測できれば、分析は重回帰分析により推定することが可能である
fit2 = lm(E ~ K+U, data=dat)
summary(fit2)
Call:
lm(formula = E ~ K + U, data = dat)
Residuals:
Min 1Q Median 3Q Max
-1.57970 -0.43585 -0.00563 0.43341 2.27347
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.722e-17 2.840e-02 0.00 1
K 6.173e-01 3.589e-02 17.20 <2e-16 ***
U -9.761e-01 3.589e-02 -27.19 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6351 on 497 degrees of freedom
Multiple R-squared: 0.5982, Adjusted R-squared: 0.5966
F-statistic: 370 on 2 and 497 DF, p-value: < 2.2e-16
Kは0.61と真の値(0.5)に近い数字が推定できた。しかし、現実データには未観測の交絡要因は観測できないため、回帰分析に入れることはできない。
RCT化するのが一番良い方法だが、これが難しい場合、どうすればよいだろうか。
一つの方法が操作変数法を使うことである。
4.操作変数法による分析
操作変数法とは、介入処置の上流の変数である「操作変数」を用いて因果効果を推定する方法である。
この場合、EとKの関係に関心があるため、Eに影響を与えず、Kだけに影響を及ぼすことが明らかなQの観測値を用いて、EとKの関係を推定する。
まず、ここで回帰分析における回帰係数を考えてみる。
係数をそれぞれ次のとおりとする。
K –> E :bKE
Q –> K :bQK
Q –> E :bQE
ここで、bQK x bKE = bQE になるため、bKE = bQE / bQK となる。
fit3 = lm(E ~ Q, data=dat) #bQE
fit4 = lm(K ~ Q, data=dat) #bQK
bKE = bQE / bQK を計算する
fit3$coefficients[2]/fit4$coefficients[2] #bKE
Q
0.5367118
0.53と真の値(0.5)に近い値を推定することができた。
5.ベイズ統計による分析
操作変数法をベイズ統計を使ってやってみる。
EとKを共通の多変量正規分布に由来するものとして定義する
\begin{pmatrix}
E_i\\
K_i
\end{pmatrix} \sim MVNormal \begin{pmatrix} \begin{pmatrix} \mu_{E,i} \\ \mu_{K,i} \end{pmatrix} , S \end{pmatrix}
\mu_{E,i}= \alpha_{E}+\beta_{KE}K_i
\mu_{K,i}=\alpha_{K}+\beta_{QK}Q_i
1行目の行列Sは、EとK間の誤差項の共分散を示す。
上記は多変量線形モデルであり、複数の同時結果を持つ回帰で、すべてが共同誤差構造でモデルされてる。
各変数は、それ自身の線形モデルを得て、2つの μ 定義が得られる。KがEに影響を与える可能性があり、EとKの値のペアには何らかの相関関係がある可能性をモデルにしている。 この相関関係は、未観測の交絡Uによって生じると仮定している。(未観測Uは直接モデル化されていない)
Stan_Code filename=”mod.stan”とした。
data{
int N;
vector[N] E;
vector[N] K;
vector[N] Q;
}
parameters {
real aK;
real aE;
real bKE;
real bQK;
corr_matrix[2] Rho;
vector<lower=0>[2] Sigma;
}
transformed parameters{
vector[2] MU[N];
vector[2] YY[N];
vector[N] mu_e;
vector[N] mu_k;
for (j in 1:N) {
mu_e[j] = aE + bKE * K[j];
mu_k[j] = aK + bQK * Q[j];
}
for (j in 1:N) {
MU[j] = [mu_e[j], mu_k[j]]';
YY[j] = [E[j], K[j]]';
}
}
model {
Sigma ~ exponential(1);
Rho ~ lkj_corr(2);
bQK ~ normal(0, 0.5);
bKE ~ normal(0, 0.5);
aE ~ normal(0, 0.2);
aK ~ normal(0, 0.2);
YY ~ multi_normal(MU, quad_form_diag(Rho, Sigma));
}
統計モデルとしてはシンプルに次の1行で表されている。
YY ~ multi_normal(MU, quad_form_diag(Rho, Sigma));
YYとMUの関係を表す多変量正規分布を示しているが、YYが、EとKのペア、MUがその予測線形モデルの結果となっている。
すなわち、EとU、その予測平均値との相関関係があることをモデルとしている(相関することが未観測Uによるものと仮定)
また多変量正規分布の分散共分散行列であるが、次の関数で示している。
quad_form_diag(Rho, Sigma)
この関数は、分散共分散行列を分散の対角行列と相関行列に分解する。
Σ:分散共分散行列
D:標準偏差の対角行列
\left( \begin{array}{}
\sigma_1& 0 \\ 0 & \sigma_2
\end{array} \right)
R:相関行列
\left( \begin{array}{}
1 & \rho \\ \rho & 1
\end{array} \right)
ρは相関係数
分散共分散行列は次のとおり分解される
\Sigma=DRD
stanファイルをmod.stanとして、下記のとおりキックする
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())
dat_stan = list(N=nrow(dat),
E=dat$E,
K=dat$K,
Q=dat$Q
)
fit_stan <- stan(file ="input/mod.stan" , data = dat_stan)
結果を示す
fit_stan
Inference for Stan model: anon_model.
4 chains, each with iter=2000; warmup=1000; thin=1;
>post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
aK 0.00 0.00 0.03 -0.07 -0.02 0.00 0.02 0.07 3052 1
aE 0.00 0.00 0.05 -0.09 -0.03 0.00 0.03 0.10 2675 1
bKE 0.52 0.00 0.08 0.37 0.46 0.52 0.57 0.68 1778 1
bQK 0.63 0.00 0.03 0.56 0.60 0.63 0.65 0.69 2367 1
Rho[1,1] 1.00 NaN 0.00 1.00 1.00 1.00 1.00 1.00 NaN NaN
Rho[1,2] -0.57 0.00 0.05 -0.66 -0.60 -0.57 -0.54 -0.47 1845 1
Rho[2,1] -0.57 0.00 0.05 -0.66 -0.60 -0.57 -0.54 -0.47 1845 1
Rho[2,2] 1.00 0.00 0.00 1.00 1.00 1.00 1.00 1.00 3252 1
Sigma[1] 1.12 0.00 0.05 1.03 1.08 1.12 1.15 1.22 1951 1
Sigma[2] 0.78 0.00 0.02 0.74 0.77 0.78 0.80 0.84 3574 1
・・・(以下省略)・・・
bKEの係数は0.52が推定値となる(真の値0.5) 95%信用区間 [ 0.37 0.68]
相関係数(Rho[1,2])の中央値が -0.57となったので、因果関係は、Kの効果を未観測のUが打ち消している結果となった。
ベイズ統計法を使えば、信用区間がでるので統計的有意もわかり、また、未観測の交絡要因を気にしなくても良いという大きなメリットがある。そして、目的変数に影響しない操作変数を探し出せばよいだけなので、意外と使える手法ではないでしょうか。
6.参考
Statistical Rethinking A Bayesian Course with Examples in R and STAN
初めての統計的因果推論