1.はじめに
頻度統計学の95%信頼区間は勘違いしやすい概念ですので、備忘録のために整理しました。
例題
小学生6年生は、平均 149cm 標準偏差4cmのデータの確率密度関数(正規分布)に従うと仮定します。ここで小学生の平均を無作為抽出された標本から推定してみます。
10人を標本として無作為で抽出した時、この平均の推定量は、どこまで正確なのか?
まず、分散は全国同じ(母集団と同じ)と仮定します。
library(tidyverse)
rm(list=ls())
set.seed(123)
shogakusei = rnorm(100000,149,4) #全国の小学校6年生(10万人)とする:母集団
2.標本平均の計算
set.seed(12345)
d = sample(shogakusei,10,replace = F)
#標本平均
mea = mean(d)
mea
>[1] 147.5722
標本平均は約147.6と母集団平均を推定しました。
この平均のことを推定量といいます。
3.標準誤差の計算
母分散(標準偏差)は既にわかっているので、次のとおり、この標本の標準誤差が計算できる
$$
S.E=\frac{\sigma}{\sqrt{n}}
$$
se = 4/sqrt(10)
se
>[1] 1.264911
4. 95%信頼区間を作成する
標準誤差を使って95%信頼区間の作成に入りますが、まず標準正規分布(平均0、分散1)の分位点を計算します。
標準正規分布の95%(片側2.5%づつ引くので97.5%,0.025%)になる分位点を含む区間を考えます。
qnorm(0.975)
>[1] 1.959964
分位点は約1.96となりました。
data = data.frame(X=x<-seq(-3,3,len=101), Y=dnorm(x))
p = ggplot(data,aes(x=X,y=Y))
p = p + geom_path() + theme_bw() +xlab("f(x)")
p= p + geom_area(data = data %>% filter(X<= 1.96 & x>=-1.96)) +
theme_bw()+xlab("f(x)")
p
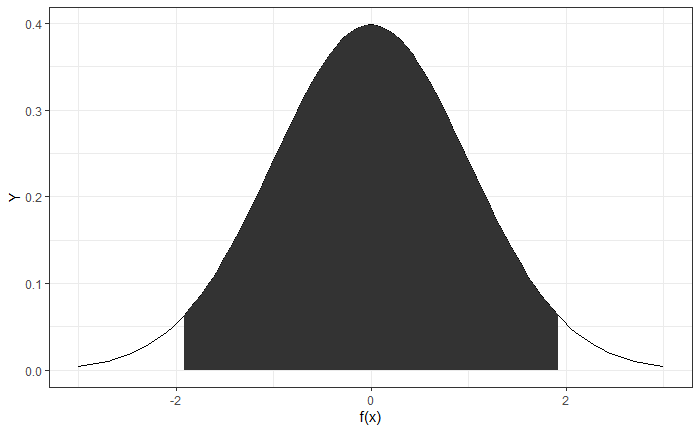
標準正規分布において、黒く塗りつぶした面積が95%になる区間(-1.96 から1.96まで)が、
95%の累積確率分布となり、xを確率変数とするf(x)は、95%の確率でこの区間に含まれます。
これを使って、95%信頼区間を作ります。
pred1 = mea + 1.96*se
pred2 = mea - 1.96*se
pred = data.frame(x=t(c(pred1,mea,pred2)))
colnames(pred)= c("lw","mean","up")
pred$time = 1
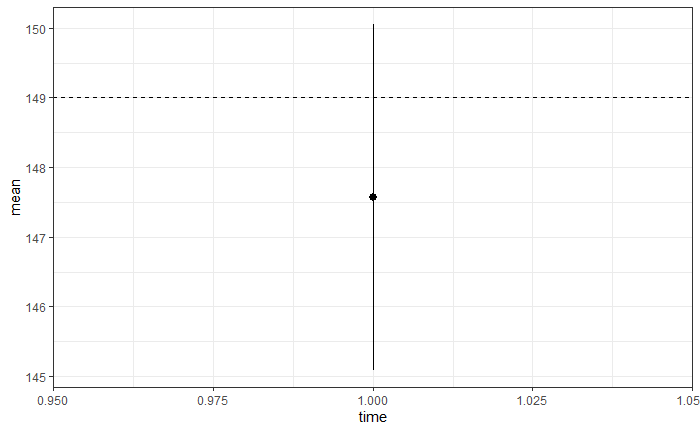
ここで、先ほどの抽出した10人を確率変数と考えると、標本平均 ± 1.96 × 標準誤差の範囲に,標本平均の推定量が95%の確率でこの範囲内に収束すると期待できます。
この時に作成した範囲の区間のことを、95%信頼区間と言います。
(この95%の確率は、あくまでも標本平均の推定量のことです)。
図で示します。
ggplot(pred) + geom_pointrange(aes(x=time,y=mean,ymin=lw,ymax=up)) +
geom_hline(yintercept = 149,linetype=2)+theme_bw()
破線が母集団の平均の真の値なので、この標本から作成した95%信頼区間の中に真の値が含まれました。
このように、真の値が含まれるか否かは、信頼区間ができあがった時点では、すでに含まれたか又は、含まれなかったかの2値しかなく、真の値はこの信頼区間の中に95%の確率で入るという言い方はできません。
確率的に動くのは標本サンプルの方なので、標本から計算する95%信頼区間を作成したら100回の内、95回、真の値が含まれることが期待できるという意味になります。
5. 95%信頼区間のシミュレーション
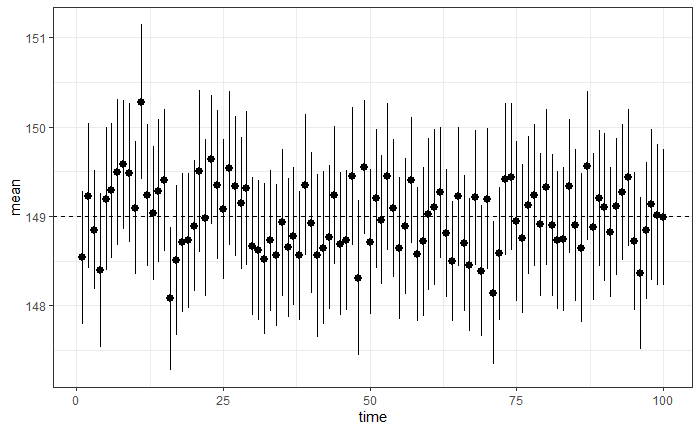
標本から100回、信頼区間を作成してシミュレーションしてみます。
set.seed(123)
d2 = replicate(100,sample(shogakusei,10,replace = F))
d3 = apply(d2,2,mean)
se = 4/sqrt(10)
d3l = d3-1.96*se
d3r = d3+1.96*se
pred = bind_cols(d3l,d3,d3r)
colnames(pred) = c("lw","mean","up")
pred$time = 1:nrow(pred)
ggplot(pred) + geom_pointrange(aes(x=time,y=mean,ymin=lw,ymax=up)) +
geom_hline(yintercept = 149,linetype=2)+theme_bw()
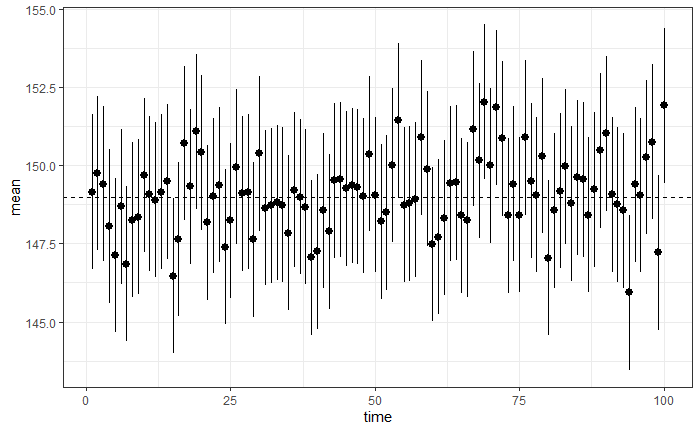
100回試行した内、何回、真の値が含まれていたのだろうか?
pred = pred %>% mutate(正解=if_else(lw <=149 & up >=149,1,0))
sum(pred$正解)
>[1] 95
このように理論値の95回に近い値がでました(このシードではちょうど95になりました)。
次に、ここまでは、母分散はわかっているという仮定でしたが、普通、母分散はわからないので、標本から計算する不偏分散を代わりに使ってみます。
不偏分散の推定量は、標本数が少ないとあまりよくないことがわかっていますので、期待値はやや下がることが予想されます。
set.seed(123)
d5 = replicate(100,sample(shogakusei,10,replace = F))
d6 = apply(d5,2,mean)
d6s = apply(d5,2,sd)
se2 = d6s/sqrt(10)
d6l = d6-1.96*se2
d6r = d6+1.96*se2
pred2 = bind_cols(d6l,d6,d6r)
colnames(pred2)=c("lw","mean","up")
pred2$time=1:nrow(pred2)
ggplot(pred2) + geom_pointrange(aes(x=time,y=mean,ymin=lw,ymax=up)) +
geom_hline(yintercept = 149,linetype=2)+theme_bw()
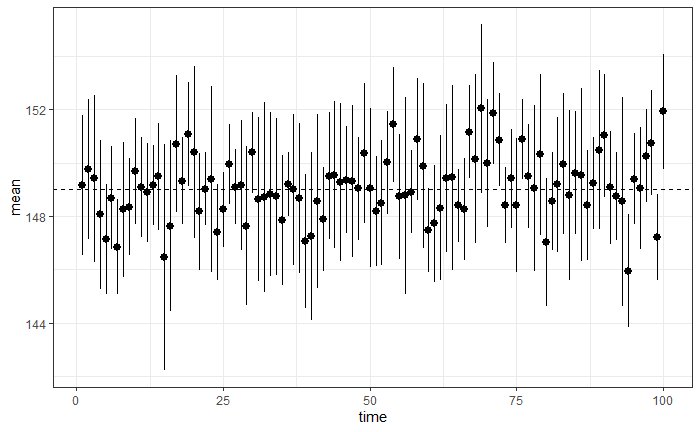
さて、正解は何個含まれていた?
pred2 = pred2 %>% mutate(正解=if_else(lw <=149 & up >=149,1,0))
sum(pred2$正解)
>[1] 90
標準誤差に、標本から計算した不偏分散を用いました。予想どおり、不偏分散は、標本サンプル数が少ない時は、精度が悪いですので、このように期待値である95回からやや低い値がでました。
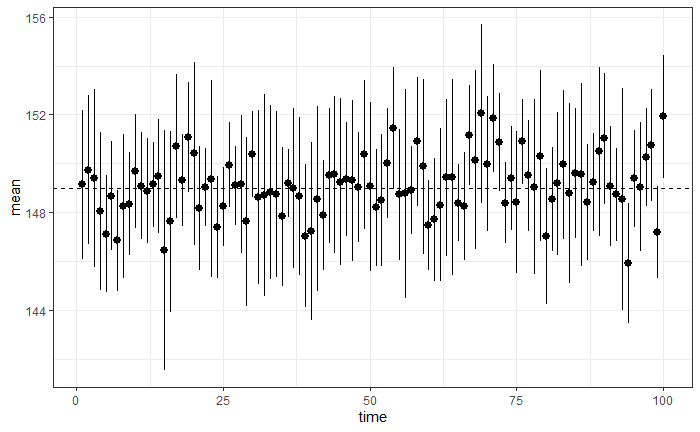
不偏分散の推定精度を上げるため、サンプルサイズを10から100に増やした場合を比較します。
set.seed(123)
d5 = replicate(100,sample(shogakusei,100,replace = F)) #100回のサンプルに変える
d6 = apply(d5,2,mean)
d6s = apply(d5,2,sd)
se2 = d6s/sqrt(100)
d6l = d6-1.96*se2
d6r = d6+1.96*se2
pred2 = bind_cols(d6l,d6,d6r)
colnames(pred2) = c("lw","mean","up")
pred2$time=1:nrow(pred2)
ggplot(pred2) + geom_pointrange(aes(x=time,y=mean,ymin=lw,ymax=up)) +
geom_hline(yintercept = 149,linetype=2)+theme_bw()
正解数は?
pred2 = pred2 %>% mutate(正解=if_else(lw <=149 & up >=149,1,0))
sum(pred2$正解)
>[1] 97
サンプルサイズを増やしたら、不偏分散による母集団の分散に対する推定量の精度があがるため、期待値である95回に近くなりました。
6.サンプルサイズが小さい場合の95%信頼区間の作成方法
このようにN数が30以下など、少数のサンプルの不偏分散を使って推定する場合は標準正規分布を使うと精度が悪くなりますが、t分布を使うと修正することができます。
data1 = data.frame(X=x<-seq(-3,3,len=101), Y=dt(x,9))
data2 = data.frame(X=x<-seq(-3,3,len=101), Y=dt(x,1))
p = ggplot(data1,aes(x=X,y=Y))
p = p + geom_path(color="red") + theme_bw()
p = p+geom_path(data=data2,color="blue")
p
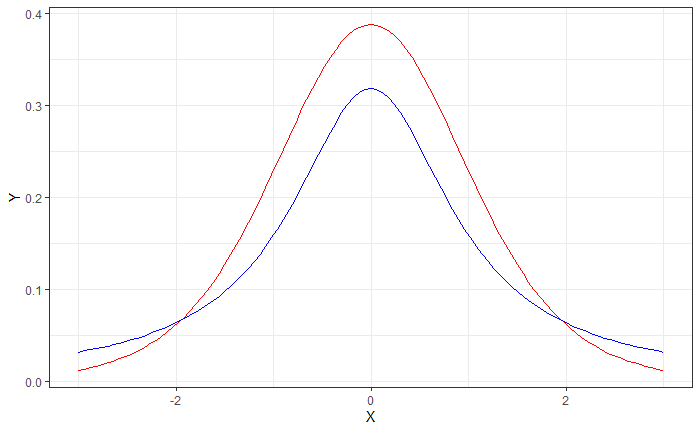
自由度9と自由度1のt分布の違い(赤が自由度9、青が自由度1)
先ほどと同じように標本数10(自由度9)の95%確率の分位点を計算します。
qt(0.975,9)
>[1] 2.262157
標準正規分布では1.96だったのと比較すると幅が広くなっています。
先ほどと同じく標本数10の不偏分散推定量を用いて、100回試行します。
set.seed(123)
t=qt(0.975,9)
d10 = replicate(100,sample(shogakusei,10,replace = F))
d11 = apply(d10,2,mean)
d11s = apply(d10,2,sd)
se3 = d11s/sqrt(10)
d11l = d11-t*se3
d11r = d11+t*se3
pred3 = bind_cols(d11l,d11,d11r)
colnames(pred3) = c("lw","mean","up")
pred3$time=1:nrow(pred3)
ggplot(pred3) + geom_pointrange(aes(x=time,y=mean,ymin=lw,ymax=up)) +
geom_hline(yintercept = 149,linetype=2)+theme_bw()
正解数は?
pred3 = pred3 %>% mutate(正解=if_else(lw <=149 & up >=149,1,0))
sum(pred3$正解)
>[1] 94
標準正規分布を用いた先ほどの90回より、理論値の95回に近づきました。
精度は向上したようです。
また、この信頼区間を使って比較し、信頼区間が重ならなければ有意水準5%で有意になる仮説検定と同意になります。この時に信頼区間の作成にt分布を用いればt検定、正規分布を用いればz検定になります。
7.おわりに
何か間違い等ございましたら、ご指摘いただけたら、大変ありがたいです。
(勉強中なものなので・・)
8.追記
信頼区間の意味は、確率的に動くのは標本サンプルの方なので、標本から計算する95%信頼区間を作成したら100回の内、95回、真の値が含まれることが期待できるという意味になると説明しましたが、人によってはこの説明はあやまりであるとの指摘がありました。
黒木さんが指摘するように確かに信頼区間の上限値、下限値は確率変数になるので、その間の区間が真の値を含む確率は95%であると言っても問題はないようにも思いました。
ちょっと統計学は思ったよりもカオスですね。