1. はじめに
意識していなかったけれど、意外にも身近なバイアスだったことに気が付きました。
自分の勉強のためにここで考えてみたいと思います。
2. DATA
ここに、ある学年100人の英語と数学の成績があります。
library(tidyverse)
set.seed(123)
eigo = floor(rnorm(100,70,20))
select =if_else(eigo>=100,TRUE , FALSE )
eigo[select==TRUE] = 100
sugaku = floor(rnorm(100,70,20))
select = if_else(sugaku>=100,TRUE , FALSE )
sugaku[select==TRUE] = 100
df = data.frame(Eigo=eigo,Sugaku=sugaku)
df$N = 1:100
dfというデーターフレーム型の変数に100人分の成績をまとめました。
数学と英語は完全に無関係に成績が作成されています。
英語ができる人と数学ができる人には相関関係はないですが、確かめてみます。
cor(df[,1:2])
> Eigo Sugaku
>Eigo 1.00000000 -0.02561039
>Sugaku -0.02561039 1.00000000
相関係数は-0.03とほとんどないことが確認できました。
成績(英語と数学の合計)のサマリーを見てみたいと思います。
gokei = df$Eigo + df$Sugaku
summary(gokei)
> Min. 1st Qu. Median Mean 3rd Qu. Max.
> 80.0 119.8 140.0 137.4 155.5 185.0
平均点は約140点、最高得点は185点、最低得点は80点でした。
3. 成績上位者
ここまでは全く普通で、特に代り映えはないですね。
さて、どこからバイアスが発生するのでしょうか。
早速、成績の分布と成績上位者(トップ10%)を見てみたいと思います。
まずは、成績上位者を抽出します。
p = 0.1
q = quantile( gokei , probs = 1-p)
slct = if_else( gokei >= q , TRUE , FALSE )
top10 = df[slct,]
top10
> Eigo Sugaku N
>6 100 69 6
>16 100 76 16
>31 78 98 31
>36 83 92 36
>49 85 100 49
>61 77 91 61
>69 88 80 69
>70 100 77 70
>82 77 95 82
>87 91 92 87
>97 100 82 97
11人が合計の上位10%から抽出されました。
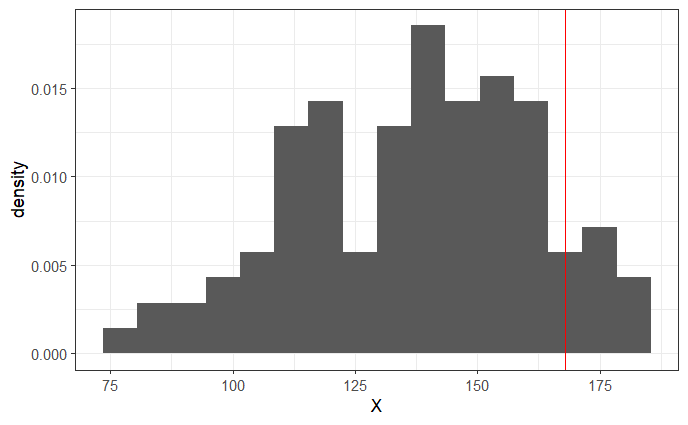
ここで成績の分布を見てみたいと思います。
d1 = data.frame(X=gokei)
ggplot(d1, aes(x=X,y=..density..)) + geom_histogram(binwidth = 7) +
geom_vline(xintercept = q, color="red") + theme_bw()
赤線が成績上位者10%の閾値を表します。
さて、成績上位者の英語と数学の成績の関係を見てみましょう。
cor(top10[,1:2])
> Eigo Sugaku
>Eigo 1.00000 -0.82022
>Sugaku -0.82022 1.00000
成績上位者は、英語と数学の成績の間に負の相関関係(r=-0.82)があり、英語ができる人は数学が苦手という傾向が見られました。
あれ❓
確か英語と数学の成績は無関係に作成したデータなのに、どこで間違ったの❓
4. 合流点バイアス
まずは、成績上位者の分布を確かめてみます。
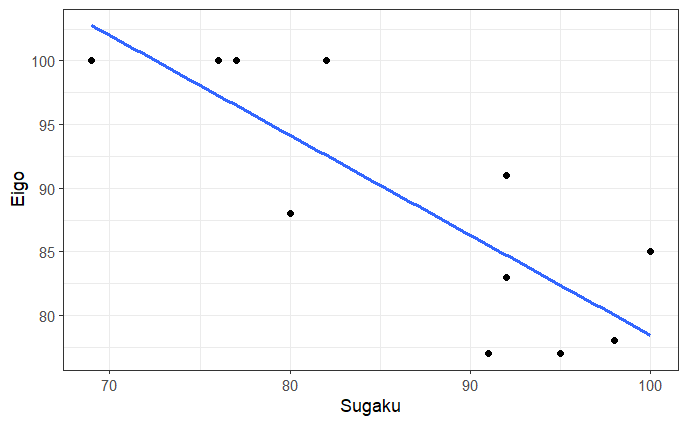
ggplot(top10,aes(x=Sugaku,y=Eigo))+geom_point()+theme_bw() +
geom_smooth(method = "lm", se=F)
確かに、相関関係がありそうですね。どこが間違っているのだろうか?
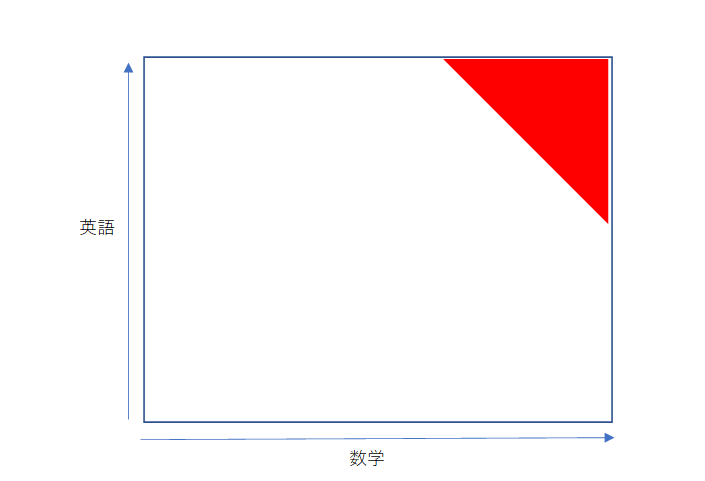
実は、これが合流点バイアス(Collider Bias)と呼ばれる現象です。
上図を見ると赤い部分が上位者に相当します。数学と英語の間には相関関係はないけれども、合計から両者を選ぶ過程において、選択バイアスがかかり、見かけ上の相関関係が発生します。
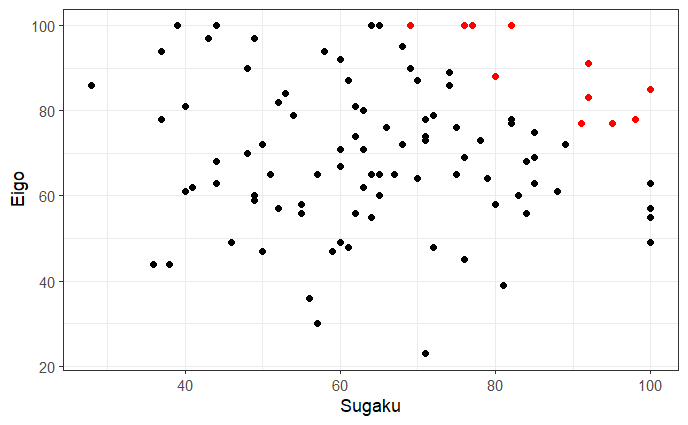
ggplot(df,aes(x=Sugaku,y=Eigo)) + geom_point() +
geom_point(data=top10,aes(x=Sugaku,y=Eigo),color="red") + theme_bw()
summary(top10)
>Eigo Sugaku N
>Min. : 77.0 Min. : 69.00 Min. : 6.00
>1st Qu.: 80.5 1st Qu.: 78.50 1st Qu.:33.50
>Median : 88.0 Median : 91.00 Median :61.00
>Mean : 89.0 Mean : 86.55 Mean :54.91
>3rd Qu.:100.0 3rd Qu.: 93.50 3rd Qu.:76.00
>Max. :100.0 Max. :100.00 Max. :97.00
赤い点が成績上位者になります。サマリーを見ても、成績上位者の英語と数学の成績に大きな差はありません。
5. まとめ
自分でも、このバイアスは不思議な気がして、しっくりとはしなかったのでRで再現してみました。合計の上位10%としたところで、選択バイアスがかかっているのです。
例えば、ニュースで、
「ある助成金審査委員会が、科学研究の提案を200件受け取り、これらの提案のうち、信頼性(厳密性、学術性、成功の可能性)とニュース性(社会福祉的価値、公共性)から審査委員会が、その合計点で順位をつけ、上位10%を助成対象として選定した。その結果、最もニュースになるような科学的研究は、最も信用できない傾向がある」といった報道がされても、りっぱな合流点バイアスですね。
バークソンのパラドックスと呼ばれることもあるそうで、「選択-歪曲効果」だそうです。
合計した結果の負の相関関係には気を付けましょう!