1.はじめに
「mlrMBOを用いたベイズ最適化」として2020年に投稿しましたが、mlrはすでにmlr3に移行しているため、情報が古くなっています。そこで最新のmlr3に対応させました。
Black-box関数最適化問題というのは,目的関数の代数的な表現,つまり,数式自体が与えられず,解に対する目的関数値のみを利用することができる問題で、これを解決する方法の一つにベイズ最適化(Bayesian Optimization)がある。Black-box関数最適化では解の1回の評価の計算コストが大きいことを前提している。
そこで、できるだけ少ない評価回数でベストなパラメータを推定する方法にベイズ最適化が用いられ、Rでは"rBayesianOptimization"パッケージが提供されている。
しかし、mlr3で提供されているベイズ最適化をするmlr3MBOパッケージについては、日本語による情報がほとんどないので、mlr3MBOパッケージによるベイズ最適化について、紹介する。
2.ベイズ最適化とは
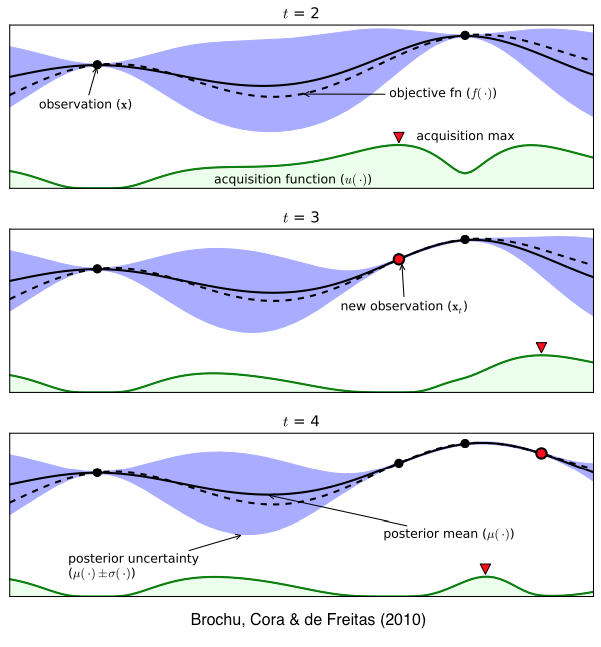
ベイズ最適化では評価に大きな計算コストのかかる目的関数の代わりに、ガウス過程回帰と獲得関数と呼ばれる代理関数を最適化することで,次の探索点を選択します。
ガウス過程回帰では、関数の事後分布を予測する(平均と分散)。上記図では青色の部分。
図下の緑色の部分は事後分布から計算された獲得関数(acquisition function)。
獲得関数が最大値をとる値が次の観測値の候補となる。
3.mlr3MBOを使ったベイズ最適化
3.1 パラメータと最小値の推定
3.1.1 Library
library(tidyverse)
library(mlr3)
library(mlr3tuning)
library(mlr3learners)
library(mlr3mbo)
library(bbotk)
3.1.2 DATA
ObjectiveRFunクラスを使って、目的となる未知の1次関数を作成します。
domainで説明変数となるパラメータ域を指定し、codomainでターゲットのパラメータを指定する。(dblは小数点を取りうる実数値を意味する)
tags="minimize"は最小方向、”maximize”は最大方向を指定します。
sim_1d = function(xs) 2*xs$x * sin(14 * xs$x)
domain = ps(x=p_dbl(lower = 0,upper = 1))
codomain = ps(y = p_dbl(tags = "minimize"))
objective = ObjectiveRFun$new(sim_1d, domain = domain, codomain = codomain)
#x軸のグリッドを作成
xydt = generate_design_grid(domain, resolution = 1001)$data
#eval_dtメソッドはデーターテーブルを関数に適用するときに使用
xydt = xydt %>% mutate(y = objective$eval_dt(xydt)$y)
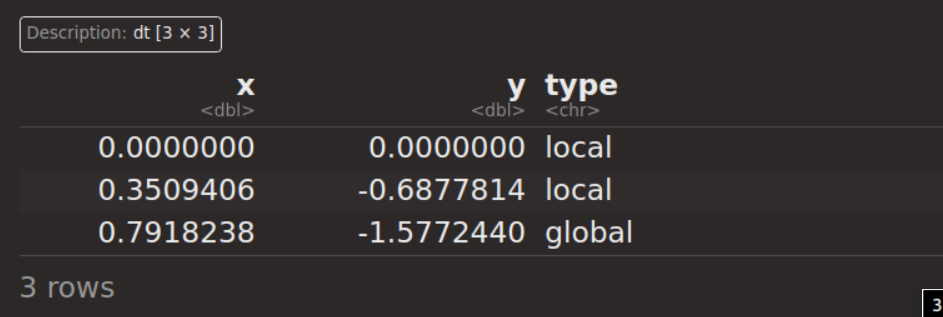
局所的最適解と大域的最適解を求める
optima = data.table(x = c(0, 0.3509406, 0.7918238))
optima = optima %>% mutate(y = objective$eval_dt(optima)$y)
optima$type = c("local", "local", "global")
optima
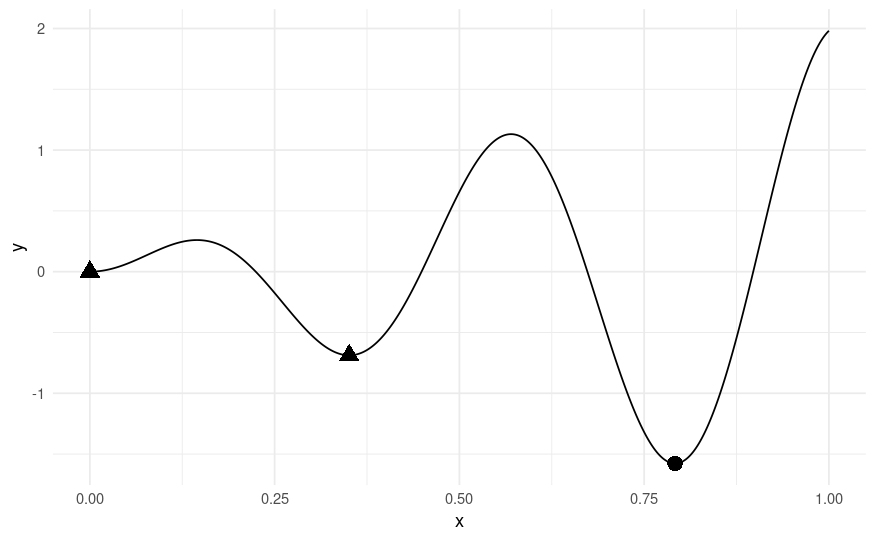
ggplot(aes(x = x, y = y), data = xydt) +
geom_line() +
geom_point(aes(pch = type), color = "black", size = 4, data = optima) +
theme_minimal() +
theme(legend.position = "none")
▲は局所的最適解での解で、x=0.792の時に●の大域的最適解となる。
3.2 ベイズ最適化の構成要素
ベイズ最適化(Bayesian Optimization : BO)は、通常、次のプロセスをたどる大域的最適化アルゴリズムである。
- 初期設計の生成と評価
- ループ関数
- 未知のブラックボックス関数をモデル化するため、初期観測値のアーカイブにサロゲートモデル(代理モデル)を適合させる
- パラメータの探索空間について、次に評価すべき有望な候補を決定するため、獲得関数を最適化させる
- 次の候補を評価し、これまでに行われた観測値のアーカイブを更新する
- 所定の終了基準を満たすかチェックし、満たさない場合は1に戻る
獲得関数は、サロゲートモデルの平均と標準偏差の予測値に依存するため、真のブラックボックス関数を評価する必要がないため、計算コストは低くなる。
良い獲得関数は、サロゲートモデルの不確実性が低い領域を知識として利用し、まだ評価していないポイントと、サロゲートモデルの不確実性が高い領域を探索することとのバランスを取る。
これらの要素をBOの”ビルディングブロック”と呼ぶ。
サロゲートモデル、獲得関数、獲得関数の最適化の各要素については、ある程度互換性があるので、mlr3mboではモジュール構造になっている。
3.2.1 初期設計
サロゲートモデルをデータに適合させる前に、初期点のデータが必要で、この初期点の集合を初期設計と呼ぶ。
- 初期設計を構築する関数
generate_design_random:ランダムに一様な点を生成
generate_design_grid:一様な大きさの格子状に点を生成
generate_design_lhs:ラテン超立方体サンプリング
generate_design_sobol:sobol数列を生成
BOでは通常LHSまたはSobol設計が推奨され、Grid設計は、通常、推奨されない。
今回の事例では、初期設計はカスタム値を用いることとし、まずOptimInstanceクラスで評価し、アーカイブする。
instance = OptimInstanceBatchSingleCrit$new(objective,
terminator = trm("evals", n_evals = 20))
design = data.table(x = c(0.1, 0.34, 0.65, 1))
instance$eval_batch(design)
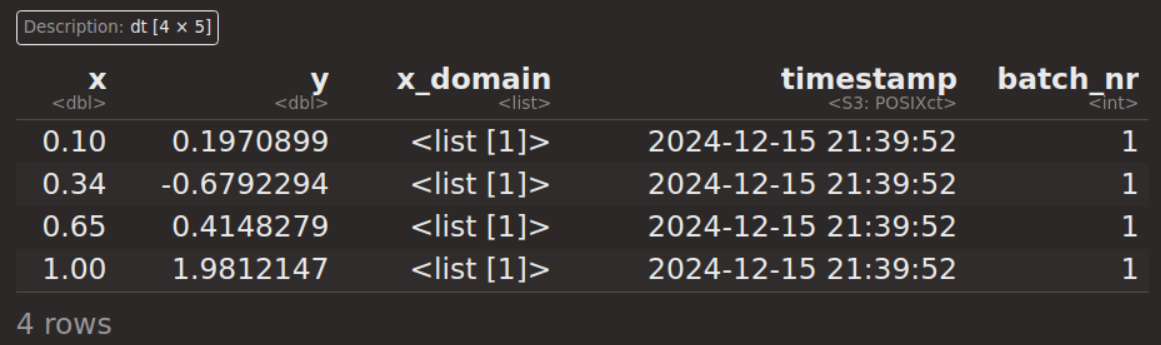
instance$archive$data
初期設計のポイントが、どのように評価されたかの一覧で、この結果をサロゲートモデルにフィットさせることから、BOアルゴリズムが始まる。
3.2.2 サロゲートモデル(代理モデル)
サロゲートモデルは、観測値に基づき未知のブラックボックス関数をモデル化するための回帰モデルの学習器を含む。mlr3ではどの学習器も使用可能だが、その予測値に標準偏差がサポートされている必要があり、全ての学習器が実際に使える訳ではない。低から中次元の探索空間では、ガウス過程回帰、高次元の探索空間ではランダムフォレスト回帰が用いられる。
この事例では、Matern 5/2カーネルのガウス過程回帰を用い、オプティマイザーとしてBFGSを用いる。
lrn_gp = lrn("regr.km", covtype = "matern5_2", optim.method = "BFGS",
control = list(trace = FALSE))
学習器を、インスタンスのアーカイブと一緒に渡してサロゲートモデルとする。
surrogate = srlrn(lrn_gp, archive = instance$archive)
初期設計のデータをアーカイブしているので、すぐにガウス過程回帰にフィットするサロゲートモデルを更新することができる。
surrogate$update()
surrogate$learner$model
#> Call:
#> DiceKriging::km(design = data, response = task$truth(), covtype = "matern5_2",
#> optim.method = "BFGS", control = pv$control)
#>
#> Trend coeff.:
#> Estimate
#> (Intercept) 0.7899
#>
#> Covar. type : matern5_2
#> Covar. coeff.:
#> Estimate
#> theta(x) 0.3014
#>
#> Variance estimate: 1.069737
3.2.3 獲得関数
獲得関数はサロゲートモデルの予測に依存し、探索空間における各ポイントが次の反復で評価された場合の期待度を定量化する。
良く用いられる例が期待改善度で、候補点がこれまに観察された最良の関数値よりどれだけ改善されるかを示す:
$$
\alpha_{EI}=\mathbb{E} [\max\left(f_{\mathrm{min}}-Y(\mathbf{x}),0,\right]
$$
本事例では このacqf(”ei”)を用いる。
その他、mlr3ではmlr_acqfunctions辞書に使用可能な獲得関数(クラス)が格納されている。
mlr_acqfunctions
#> <DictionaryAcqFunction> with 13 stored values
#> Keys: aei, cb, ehvi, ehvigh, ei, eips, mean, multi, pi, sd, smsego,
#> stochastic_cb, stochastic_ei
現在は13種類ある。
“ei”の獲得関数を適用する。
acq_function = acqf("ei", surrogate = surrogate)
acq_function$update()
xydt = generate_design_grid(domain, resolution = 1001)$data
# evaluate our sinusoidal function
xydt[, y := objective$eval_dt(xydt)$y]
# evaluate expected improvement
xydt[, ei := acq_function$eval_dt(xydt[, "x"])]
xydt[, c("mean", "se") := surrogate$predict(xydt[, "x"])]
ggplot(xydt, mapping = aes(x = x, y = y)) +
geom_point(size = 2, data = instance$archive$data) +
geom_line() +
geom_line(aes(y = mean), colour = "gray", linetype = 2) +
geom_ribbon(aes(min = mean - se, max = mean + se),
fill = "gray", alpha = 0.3) +
geom_line(aes(y = ei * 40), linewidth = 1, colour = "green") +
scale_y_continuous("y",
sec.axis = sec_axis(~ . * 0.025, name = "EI",
breaks = c(0, 0.025, 0.05))) +
theme_minimal()
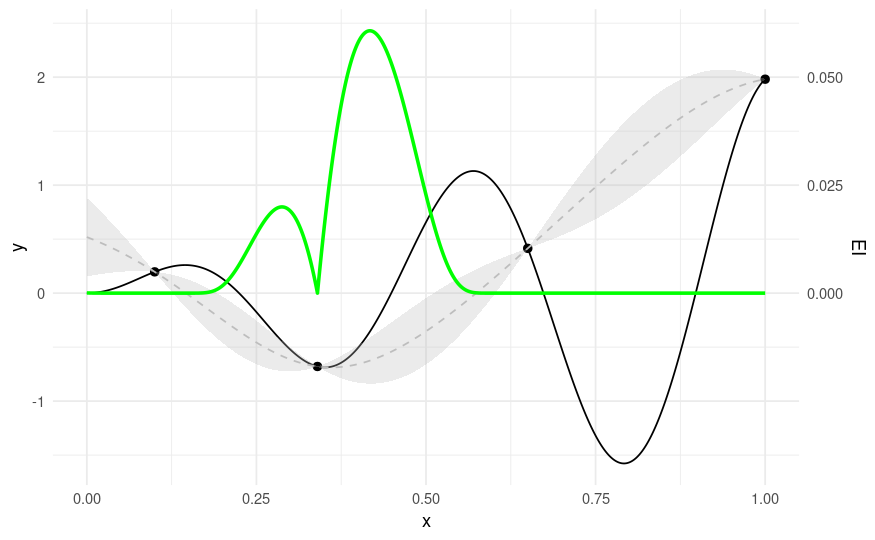
4点の初期設計で学習したガウス過程回帰モデルの平均と標準偏差の予測から求めた期待改善度(緑色)。灰色は、ガウス過程回帰の予測した標準偏差(不確実性を示す)。
3.2.4 獲得関数の最適化
獲得関数自体の最適はには、大域的な最適化手法であるDIRECTアルゴリズムを用いる。
AcqOptimizerクラスはacqo()で構築し、100回反復しても1e-5の改善が見られなければ終了させるアルゴリズムである。
acq_optimizer = acqo(opt("nloptr", algorithm = "NLOPT_GN_ORIG_DIRECT"),
terminator = trm("stagnation", iters = 100, threshold = 1e-5),
acq_function = acq_function)
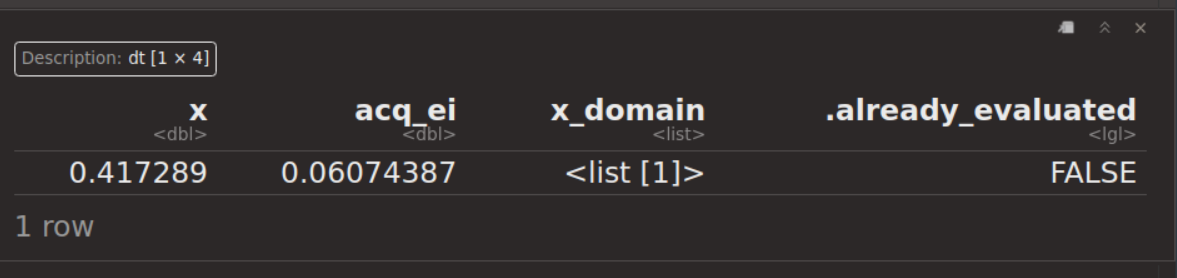
candiate = acq_optimizer$optimize()
candiate
3.2.5 ループ関数
MLR3で使用できるBOアルゴリズムのループ関数は次のとおり。
mlr_loop_functions
#> <DictionaryLoopFunction> with 5 stored values
#> Keys: bayesopt_ego, bayesopt_emo, bayesopt_mpcl, bayesopt_parego,
#> bayesopt_smsego
れらの内、bayesopt_egoが最も一般的によく使われるループ関数である。OptimizeMbo【opt()】を使用すると、BOアルゴリズムである”ビルディング・ブロック”を最適化する単一オブジェクトにできる。
bayesopt_ego = mlr_loop_functions$get("bayesopt_ego")
acq_function = acqf("ei")
acq_optimizer = acqo(opt("nloptr", algorithm = "NLOPT_GN_ORIG_DIRECT"),
terminator = trm("stagnation", iters = 100, threshold = 1e-5))
optimizer = opt("mbo",
loop_function = bayesopt_ego,
surrogate = surrogate,
acq_function = acq_function,
acq_optimizer = acq_optimizer)
前述のOptimInstanceクラスを用いて作成した初期設計を再び用いる。初期点の構成は、自動ではなくカスタムを用いる。
instance = OptimInstanceBatchSingleCrit$new(objective,
terminator = trm("evals", n_evals = 20))
design = data.table(x = c(0.1, 0.34, 0.65, 1))
初期設計を適用し、BOアルゴリズムでループを回し、最適化する。
instance$eval_batch(design)
optimizer$optimize(instance)
#> INFO [19:33:37.506] [bbotk] Evaluating 4 configuration(s)
#> INFO [19:33:37.532] [bbotk] Result of batch 1:
#> INFO [19:33:37.543] [bbotk]
#> INFO [19:33:37.608] [bbotk] Starting to optimize 1 parameter(s) with '<OptimizerMbo>' and '<TerminatorEvals> [n_evals=20, k=0]'
#> INFO [19:33:38.996] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:39.006] [bbotk] Result of batch 2:
#> INFO [19:33:39.016] [bbotk]
#> INFO [19:33:40.251] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:40.262] [bbotk] Result of batch 3:
#> INFO [19:33:40.272] [bbotk]
#> INFO [19:33:41.716] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:41.728] [bbotk] Result of batch 4:
#> INFO [19:33:41.739] [bbotk]
#> INFO [19:33:43.358] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:43.368] [bbotk] Result of batch 5:
#> INFO [19:33:43.378] [bbotk]
#> INFO [19:33:45.187] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:45.198] [bbotk] Result of batch 6:
#> INFO [19:33:45.208] [bbotk]
#> INFO [19:33:46.519] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:46.529] [bbotk] Result of batch 7:
#> INFO [19:33:46.539] [bbotk]
#> INFO [19:33:47.692] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:47.702] [bbotk] Result of batch 8:
#> INFO [19:33:47.712] [bbotk]
#> INFO [19:33:49.135] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:49.151] [bbotk] Result of batch 9:
#> INFO [19:33:49.163] [bbotk]
#> INFO [19:33:51.495] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:51.525] [bbotk] Result of batch 10:
#> INFO [19:33:51.537] [bbotk]
#> INFO [19:33:55.952] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:55.962] [bbotk] Result of batch 11:
#> INFO [19:33:55.973] [bbotk]
#> INFO [19:33:58.471] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:33:58.481] [bbotk] Result of batch 12:
#> INFO [19:33:58.491] [bbotk]
#> INFO [19:34:00.878] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:34:00.890] [bbotk] Result of batch 13:
#> INFO [19:34:00.901] [bbotk]
#> INFO [19:34:03.396] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:34:03.407] [bbotk] Result of batch 14:
#> INFO [19:34:03.418] [bbotk]
#> INFO [19:34:05.839] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:34:05.851] [bbotk] Result of batch 15:
#> INFO [19:34:05.862] [bbotk]
#> INFO [19:34:08.287] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:34:08.298] [bbotk] Result of batch 16:
#> INFO [19:34:08.308] [bbotk]
#> INFO [19:34:10.990] [bbotk] Evaluating 1 configuration(s)
#> INFO [19:34:11.000] [bbotk] Result of batch 17:
#> INFO [19:34:11.011] [bbotk]
#> INFO [19:34:11.074] [bbotk] Finished optimizing after 20 evaluation(s)
#> INFO [19:34:11.076] [bbotk] Result:
#> INFO [19:34:11.084] [bbotk]
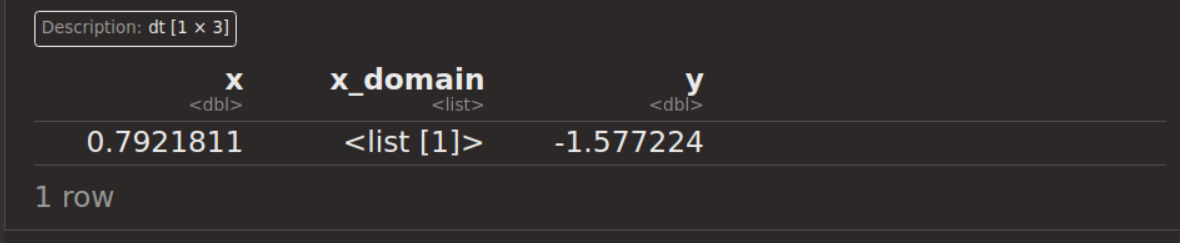
前述の未知の関数のパラメータ推定をした結果、x=0.792の時にy=-1.577と大域最適解にたどり着いた。
BOアルゴリズムのサンプリング軌跡を見てみる。
ggplot(xydt, mapping = aes(x = x, y = y)) +
geom_point(aes(color=batch_nr),size = 4, data = instance$archive$data) +
geom_line() + theme_minimal()
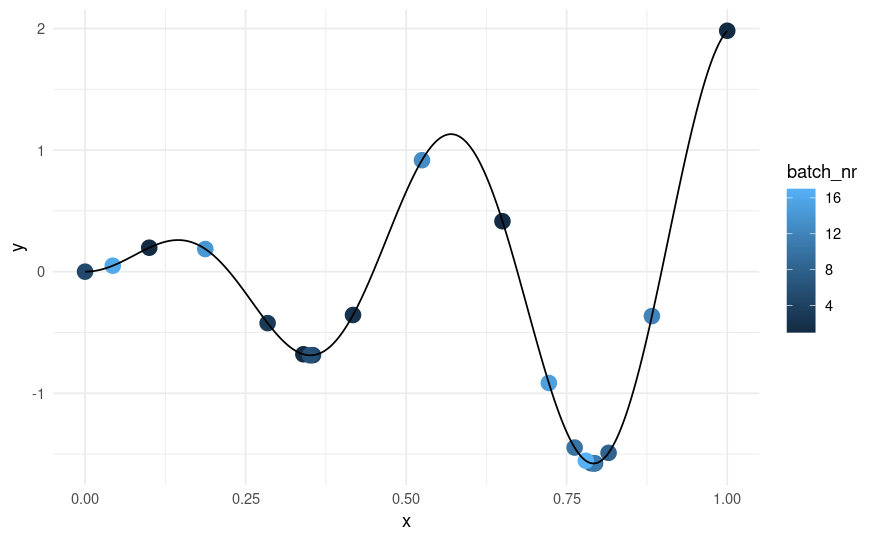
アルゴリズムにより学習が進んだことを示す大域最適解付近に薄い青色が集中している。
4 2変数を用いたベイズ最適化
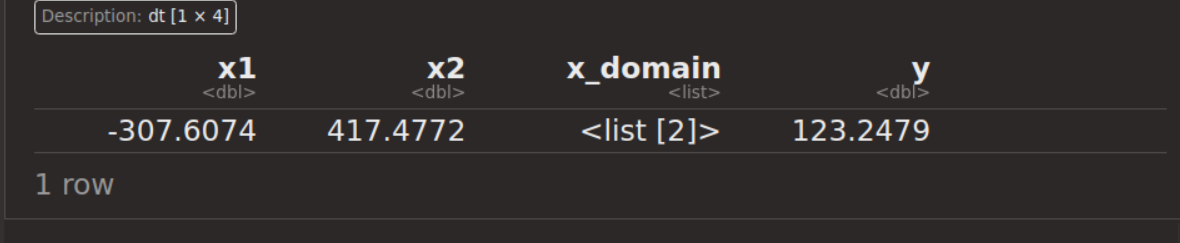
目的となる未知の関数は、かなり複雑な形状をもつ2変数x1,x2によるyの最小値を求める。
objective_function = function(xs) {
list(y = 418.9829 * 2 - (sum(unlist(xs) * sin(sqrt(abs(unlist(xs)))))))
}
domain = ps(x1 = p_dbl(lower = -500, upper = 500),
x2 = p_dbl(lower = -500, upper = 500))
codomain = ps(y = p_dbl(tags = "minimize"))
objective = ObjectiveRFun$new(
fun = objective_function,
domain = domain,
codomain = codomain)
instance = OptimInstanceBatchSingleCrit$new(
objective = objective,
search_space = domain,
terminator = trm("evals", n_evals = 60))
# Gaussian Process, EI, DIRECT
surrogate = srlrn(default_gp())
acq_function = acqf("ei")
acq_optimizer = acqo(opt("nloptr", algorithm = "NLOPT_GN_DIRECT_L"),
terminator = trm("stagnation", threshold = 1e-8))
optimizer = opt("mbo",
loop_function = bayesopt_ego,
surrogate = surrogate,
acq_function = acq_function,
acq_optimizer = acq_optimizer)
set.seed(2906)
optimizer$optimize(instance)
xdt = generate_design_grid(instance$search_space, resolution = 101)$data
ydt = objective$eval_dt(xdt)
ggplot(aes(x = x1, y = x2, z = y), data = cbind(xdt, ydt)) +
geom_contour_filled() +
geom_point(aes(color = batch_nr), size = 2, data = instance$archive$data) +
scale_color_gradient(low = "lightgrey", high = "red") +
theme_minimal()
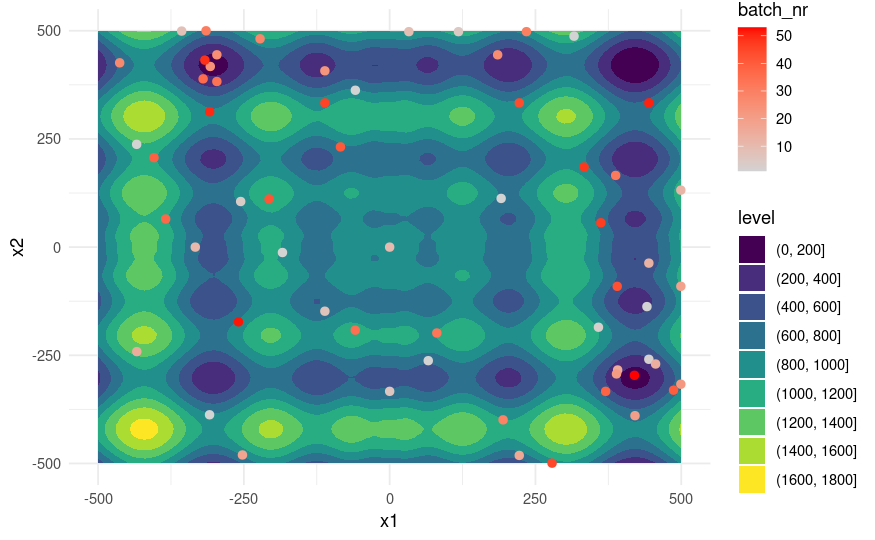
色が濃い青になっている部分がyの値が低い底値になるが、学習が進み、赤色に変化するとともに青色の部分に集まっている。効率的にパラメータ探索ができていることがよくわかる。
5.参考
5 Advanced Tuning Methods and Black Box Optimization