状態空間モデルを使った変化点検出の試み（その２）

1.はじめに

前回、状態空間モデルを使ってナイル川の流量データから変化点を読み取り、ダムの建設年代を推定しました。
KFASパッケージを使ったガウス状態空間モデルによる変化点検出の試み
今回は、その続きになります。

まず、前回の結果を図示化します。

2.KFASパッケージによる平滑化の図示化

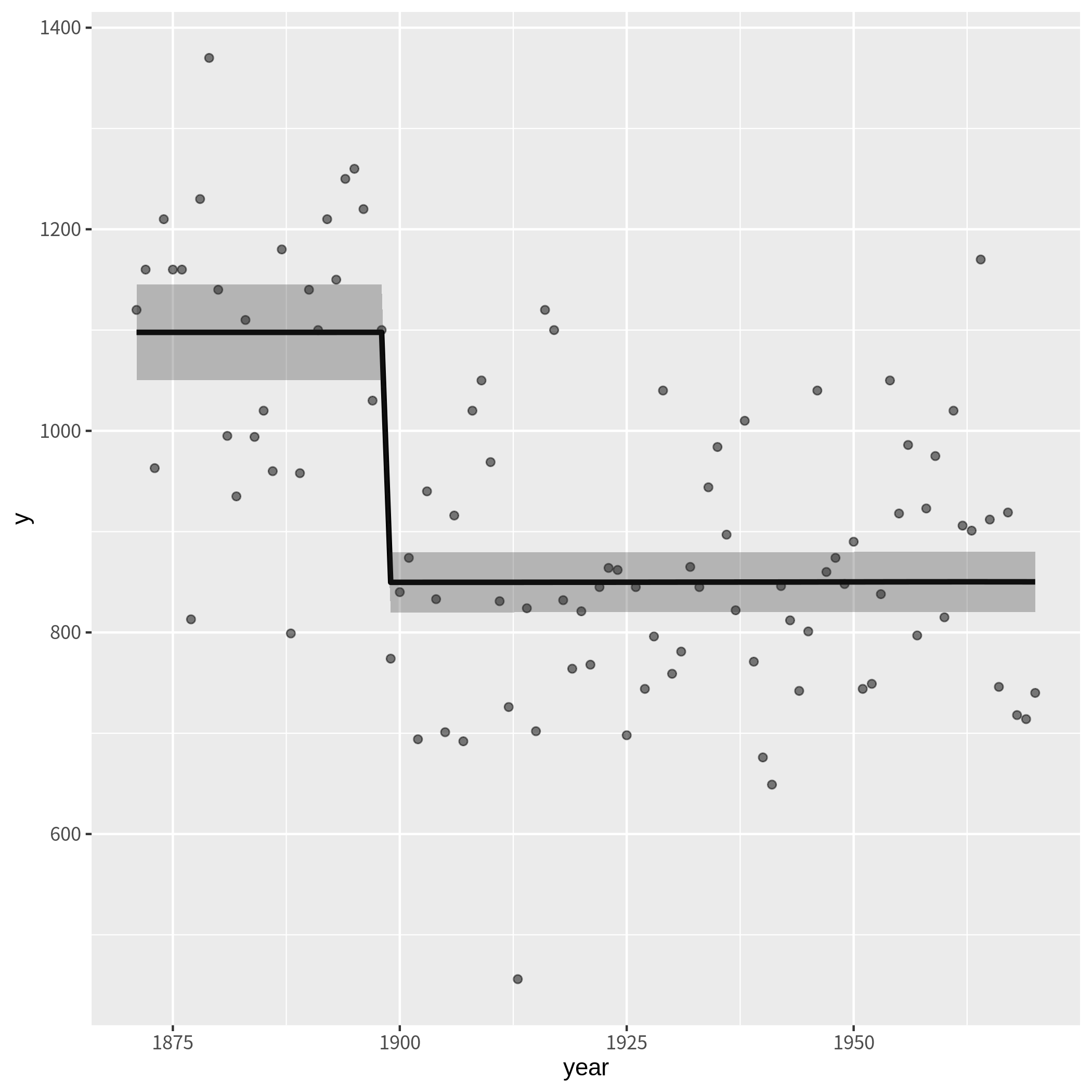
外生変数(dam)を1871から1898年は0に、1899年から1にした状態空間モデルによる平滑化を図示化します。

library(tidyverse)
library(KFAS)

d = Nile
t_max　=　length(d)

year_dam = rep(0,t_max)
year_dam[which(1899 <=time(d))] =1
df = data.frame(y=d, dam=year_dam,year=1871:1970)

build_reg = SSModel(H=NA, y ~SSMtrend(degree=1, Q=NA) +
                      SSMregression(~ dam, Q=NA), data = df)

fit_reg = fitSSM(build_reg,inits = c(1,1,1))

result_reg = KFS(
  fit_reg$model,
  filtering = c("state","mean"),
  smoothing = c("state","mean")
)
interval_conf = predict(fit_reg$model,
                       interval = "confidence",level=0.95)
interval_conf = data.frame(interval_conf)
data = bind_cols(df,interval_conf)

ggplot(data,aes(x=year,y=y)) +
  geom_point(alpha=0.5) +
  geom_line(aes(y=fit),size=1.2) +
  geom_ribbon(aes(ymin=lwr,ymax=upr),alpha=0.3)

次はベイズ推定法を使ってみたいと思います。

RStanパッケージを使ってStanを動かします。
Stanとは確率的プログラミング言語の一つで、統計モデリングに特化したプログラミング言語です。
詳しくは、参考の「StanとRで統計モデリング」松浦健太郎　著者の本を参考にしてください。統計モデリングを学ぶのに非常に優れた本です。

3.RStanによる平滑化

「StanとRで統計モデリング」のChapter12.3　変化点検出を参考にしました。
状態方程式に正規分布から裾の広いコーシー分布に置き換えることで、状態の分散の変動の変化点を捉えることができます。
Stanでのベクトル表現によるローカルレベルの実装例です。

model{
 mu[1] ~ normal(mu_zero, s_w);
 mu[2:N] ~ normal(mu[1:N-1] , s_w); //状態方程式
 Y ~ normal(mu , s_v);  //観測方程式
}

上記の状態方程式の正規分布(normal)関数を、コーシー分布(cauchy)関数に置き換えるだけで、変化点の検出に対応したモデルとなるのですが、そのままでは収束性が悪くなります。

そこで逆関数法を用いた乱数生成を用います。
Cachy分布の確率密度関数は次のとおりです。

$$
f(x)=\frac{1}{\pi(1+x^2)}
$$
この累積分布関数は、

$$
F(y)=\frac{1}{\pi}arctan(\frac{y-\mu}{\sigma})+0.5
$$
になりますが、逆関数は次のようになります。
$$
F^{-1}=\mu+\sigma tan(\pi(x-0.5))
$$
[0,1]の一様分布に従う乱数を生成して逆関数に当てはめることで、目的とする累積分布関数に従う乱数を形成することができます。

stan codeとRのcodeは次のとおりです。

stan_code="
data {
  int<lower=0> N;
  vector[N] Y;
 }

parameters {
  real mu_zero;
  real<lower=0> s_v; //観測誤差の標準偏差
  real<lower=0> s_w; //状態誤差の標準偏差
  vector<lower= -pi()/2, upper= pi()/2>[N-1] mu_raw;  //
}

transformed parameters{
   vector[N] mu;
   mu[1] = mu_zero;
   for(t in 2:N) 
     mu[t] = mu[t-1] + s_w*tan(mu_raw[t-1]); //逆関数法
}

model {
  Y ~ normal(mu , s_v);  //観測方程式
 }
"
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

n = nrow(df)
data = list(N=n,Y=df$y)
mod = stan_model(model_code = stan_code)
fit = sampling(mod, data=data,
           iter=4000,thin=1,warmup=2000,
           control = list(max_treedepth = 20),
           seed=1234)

$> 省略
$>Chain 4: Iteration: 4000 / 4000 [100%]  (Sampling)
$>Chain 4: 
$>Chain 4:  Elapsed Time: 14.0831 seconds (Warm-up)
$>Chain 4:                14.4954 seconds (Sampling)
$>Chain 4:                28.5785 seconds (Total)
$>Chain 4: 
$>There were 16 divergent transitions after warmup. See
$>http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
$>to find out why this is a problem and how to eliminate them.Examine the pairs() plot to diagnose sampling problems

次に、無事に収束しているかどうかを見てみます。

library(bayesplot)
mcmc_rhat(rhat(fit))
mcmc_combo(fit, pars = c("s_w", "s_v"))

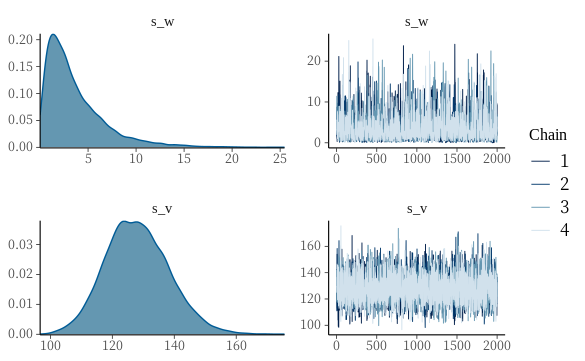
結果は、Rhatは全て1.05以下で、トレースプロットを見ても、Chainがよく混ざっていることがわかります。

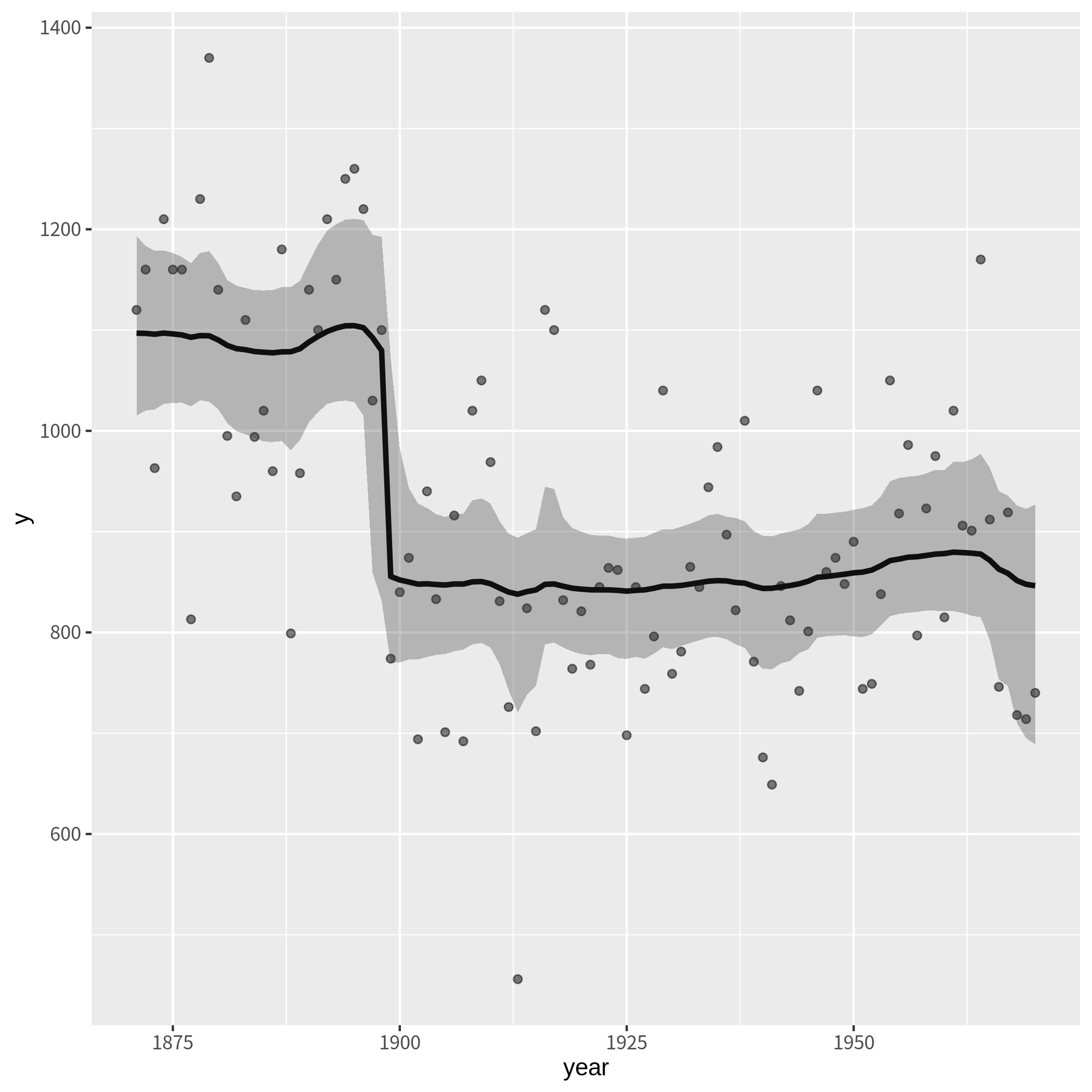
それでは、図示化します。

result=rstan::extract(fit)    
model_mu_smooth = t(apply(result$mu,2,quantile,
                              probs=c(0.025,0.5,0.975)))
model_mu_smooth = as.data.frame(model_mu_smooth)

data= bind_cols(df,model_mu_smooth)

ggplot(data,aes(x=year,y=y)) +
  geom_point(alpha=0.5) +
  geom_line(aes(y=`50%`),size=1.2) +
  geom_ribbon(aes(ymin=`2.5%`,ymax=`97.5%`),alpha=0.3)

KFASで外生変数を使った結果とほぼ同じになりました。

最後に、bstsというパッケージを使ってみます。

4.bstsによる平滑化

bstsはベイズ構造時系列モデリングを行うパッケージです。
bsts とは, Bayesian Structural Time Series, ベイズ (ベイジアン) 構造時系列モデルの略称です。
状態空間モデルを使ってベイズ推定します。

詳しくは、次を見てください。
[R] bsts (ベイズ構造時系列モデル) パッケージの使い方

bstsでは、説明変数の事前分布にspike-and-slab分布を用いることで、変数の選択を可能にしています。
影響がなければ、変数の係数が0になることを利用して、ダム建設による変化点の抽出を試みます。
係数の推定値は事後分布の中央値を用います。
1871年から1970年まで、dam説明変数を用いています。damが建設されると1をとります。
100回繰り返しているので、この計算は少し時間がかかります。

library(bsts)

d = Nile
t_max　=　length(d)
reg=0
set.seed(123)
for(i in 1:100) {

year_dam = rep(0,t_max)
year_dam[which(1870+i <=time(d))] =1
df = data.frame(y=d, dam=year_dam,year=1871:1970)

#状態空間モデルのローカルレベルを指定
ss = AddLocalLevel(state.specification=list(), df$y)

bsts_model = bsts(y ~ dam, #回帰モデルの指定
               state.specification = ss,
               niter = 1000,
               data = df)
reg = c(reg,median(bsts_model$coefficients[,2]))
}
reg = reg[-1]

もっとも流量の減少が大きかった年を推定します。

reg_df　= data.frame(time = 1871:1970, coef =reg)
reg_df[which.min(reg_df$coef),]
ggplot(reg_df,aes(x=time,y=coef)) + geom_bar(stat="identity")

1899年が最も流量に影響を与えています。

KFASで外生変数を使う場合より、こちらの方がいいですね。
bstsは面白そうなパッケージなので、また後日いろいろと試してみたいと思います。

5.まとめ

KFASやbstsのパッケージを使うと便利ですが、ともすればブラックボックス的になってしまいます。
その点、RStanを使うのは正直疲れますが、理論的なところがよくわかるようになります。

6.参考

松浦健太郎(2016),StanとRでベイズ統計モデリング (Wonderful R), 共立出版