猫でもわかる量子計算によるデリバティブ価格決定

こちらに移転しました

本稿は量子コンピューター Advent Calendar 2019の記事です．

みなさん，資産運用してますか？
現金と違って，株などを持っていると常に価格変動のリスクに晒されます．
出来るだけリスクを抑えたい，でも収益も欲しい！このバランスは様々です．
どうやってそのリスクとリターンをコントロールするのか．

金融資産以外で考えてみるともっと身近なものに保険という商品があります．例えば生命保険は保険料を払うことで将来の死亡や病気の(金銭的な)リスクをコントロールする商品と見ることもできます．

同じように，デリバティブと呼ばれる価格変動リスクをコントロールするための金融商品が存在します．このような金融商品の価格はいくらが適正か？というのがデリバティブ価格決定問題です．

デリバティブについての標準的な教科書としてはHull本が挙げられます．

デリバティブの価格決定は，問題によっては非常に大量の計算量を必要とします．量子計算をうまく用いることで価格決定に必要な計算量を削減できるので嬉しい，という構造になっています．

そのため，本稿では量子計算を用いてデリバティブの価格を決定していこうと思います．紹介する量子アルゴリズムは¹に基づいています．

本稿では

1. デリバティブ
2. ヨーロピアンオプションの価格決定問題
3. モンテカルロ法
4. 量子アルゴリズム

の順で紹介していきます．デリバティブの価格決定問題に詳しい方は4. 量子アルゴリズムから読み始めることをおすすめします．

1. デリバティブ

デリバティブについてもう少し詳しく見ていきましょう．
デリバティブ(derivative)とは金融"派生"商品とも呼ばれます．
金融派生商品は「ある資産(例えば株)の価格を参照してその価値が決まる金融商品」という意味で現資産から派生しています．

これだと抽象的すぎてよくわからないので具体例をあげてみます．
「トヨタ株のヨーロピアンプットオプション」というデリバティブは予め決められた期日(満期という．例えば6ヶ月後の第二金曜日)に予め決められた価格(権利行使価格という．例えば8,000円)でトヨタ株を売る権利(プットオプションという．買う権利はコールオプション)です．

ここで，例えば6ヶ月後のトヨタ株が7,500円であれば500円もらえます．
これは，8,000円で売る権利を持っているので市場で7,500円でトヨタ株を買ってきて即8,000円で売れば500円儲かるという話です
一方，8,500円であれば0円です．
なぜかというと売る権利なので行使しなくても良いからです．

オプションと呼ばれるデリバティブはこのような権利の取引となっています．
オプションにも色々な種類があり，株価を参照する以外にも金利や債券の価格を参照したものや，権利行使のタイミングが複数存在するもの，払い戻しの条件がもっと複雑なものが存在します．

このような金融商品の価格を決定することは自明な問題ではなさそうです．
本稿ではデリバティブの中でも特にヨーロピアンオプションと呼ばれるオプションの価格決定問題を扱います．他のデリバティブとしては先物などがあり，またオプションの中でもアメリカンオプション等の興味深い問題もありますが，本稿では扱いません．

2. ヨーロピアンオプションの価格決定問題

オプションの中でも最も簡単なヨーロピアンオプションについてその価格決定を考えてみましょう．
ヨーロピアンオプションとは予め決められた期日(満期$T$)において権利行使可能なオプションの事を言います．
権利行使のタイミングが異なる他のオプションとしてはアメリカンオプションと呼ばれるものが存在し，アメリカンオプションは満期までの任意のタイミングにおいて権利行使可能なオプションのことを言います．
ヨーロピアンオプションとアメリカンオプションの中間の性質を持ったバミューダオプションは満期までの複数のあるタイミングにおいて権利行使可能なオプションのことを言います．

オプションの価格$C$は何に依存するかを考えてみると

• 権利行使価格$K(>0)$
• 満期$T(>0)$
• 金利$R(t), t \in [0, T]$
• 資産の(将来の)価格変動$S(t), t \in [0, T]$

が挙げられます．
ここで，$K$と$T$はパラメータです．

そうすると，金利と資産の(将来の)価格変動を考えていけば良さそうです．
なぜ金利に依存するかは直感的にはよくわからないと思うので，まずは金利について考えていきましょう．本稿では簡単のために金利が固定された世界$R(t)=r[1/\mathrm{year}]$を考えます．

オプションと金利

この世界では例えば100円を金利0.01で貸すと1年後に101円で返ってきます．
逆に考えると，一年後の101円の価値は現在の価値で100円となります．

同じように株の価値についても，1年後のメルカリ株の価値が5000円だった場合(!)，現在の価値は$5000/1.01\cong4950$円です．このように，将来時点での価値を現在時点での価値に換算する(割引きする)必要があります．

オプションの価格決定についても将来時点でのオプションの価値を割引いて，現在時点での価値を計算する必要があります．そのため，オプションの価格は金利に依存することになります．詳細な話は実際にオプション価格決定を行う段階ででてきます．

資産の価格変動モデル

資産の(将来の)価格変動について考えてみます．資産として株を考えてみると，株価は取引所での売買の結果によって決まります．資産の価格変動を完全な形で扱おうとすると，取引所で取引するすべての人々の資金，戦略等を考慮した上でシミュレーションを行う必要が出てきますが，東証一部だけで1日数兆円ほどの売買があります．これをすべて考慮することは実質上不可能なので，何かしらのモデル化を行う必要があります．

金融の問題では「資産の価格変動が確率過程に従う」というモデル化が多く用いられています．価格変動は人間の意思決定(どの銘柄をどれくらい買う，売るなど)の結果なので，そもそも確率的ではない(それぞれの人間の意思決定は確率的ではないはず)ですが，全参加者の意思決定を観察することもできないので，確率的に変動するものとして扱うことにしています．

一期間二項モデル

資産の価格変動について確率過程でモデル化することにしたので，オプション価格を決定する要素は揃いました．そこで，簡単なモデルでオプションの価格決定を行ってみます．

ここでは，最も簡単なモデルとして一期間二項モデルを考えてみます．
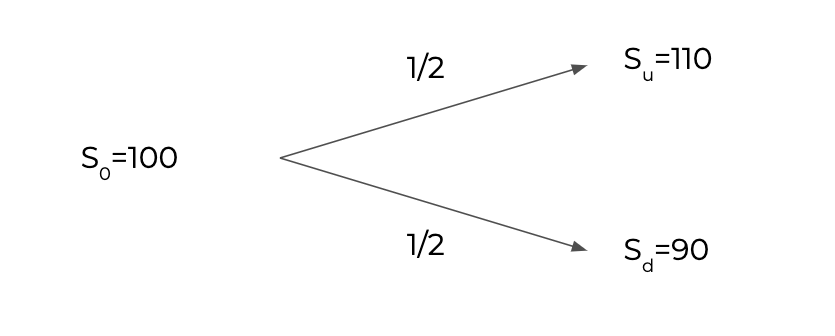
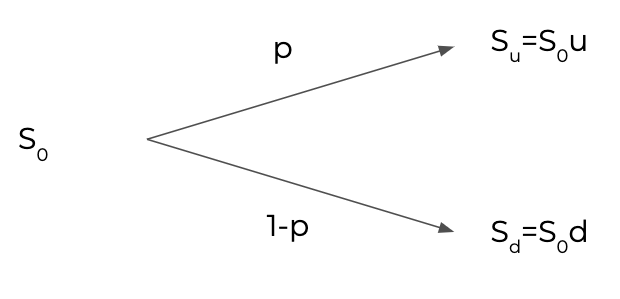
これは時間が$t \in {0, T}$の2時点だけであり，$t=T$における資産価格$S(T)$が$S(T)=S_u,S_d$の2つしかないモデルです．
$t=0$においては$S(0)=S_0$を取ります．
また，$S_u$へ遷移する確率を$p$，$S_d$へ遷移する確率を$1-p$とします．

数値例として，$S_0=100, S_u=110, S_d=95, p=1/2$とします．このとき，価格変動は下図のようになります．

さて，一期間二項モデルで価格変動をモデル化しました．
ここで求めたいのは満期が$T$で権利行使価格が$K$のオプションの価格でした．
ここでは一期間の金利が$r=0.01$で$K=95$のコールオプション($t=T$において資産1単位を$95$で買う権利)の価格を決定します．

オプションの価格決定の際に重要なのは「複数の資産がある場合に，現金の収入，支出(キャッシュフロー)が同一であればそれらの資産は同じ価値を持つ」というものです．もし，収入，支出が同一にも関わらず，価値が異なるものが存在すると，元手が0でも必ず利益を得られることになります

これに基づくと，オプションと同一のキャッシュフローを実現する資産が存在すれば，その資産の価値はオプションの価値と同一になることがわかります．これを使って$t=0$でのオプションの価値を求めることでオプションの価格$C$が決定できます．

ということでまず，コールオプションのキャッシュフローを考えます．$t=0$ではコールオプションを買うので支出が$C$となります．$t=T$では，$S(T)=110$の場合に収入が$110-95=15$で，$S(T)=90$の場合には権利行使すると損するので権利行使しないので収支は$0$です．

さて，ここで$t=0$において$y$単位の現金を借り入れ，資産を$x$単位買ったとします．このような，資産の組み合わせをポートフォリオと呼びます．ポートフォリオ自体を一つの資産として扱うことが可能です．

では，このポートフォリオのキャッシュフローを考えます．$t=0$では収支は$-100x+y$となります．$t=T$で，持っている資産をすべて売却し，借入金をすべて返済すると，$S(T)=110$の場合に$110x-1.01y$で，$S(T)=90$の場合に$90x-1.01y$となります．

各時点でのコールオプションとポートフォリオのキャッシュフローが同一になるのは

\begin{align}
  &-100x + y = -C\\
  &110x-1.01y=15 \\
  &90x-1.01y=0
\end{align}

の場合です．これを解くと$x\cong0.75,y\cong66.83, C\cong8.17$となります．
これにより，ヨーロピアンコールオプションの価格を決定することができました．

一期間二項モデルの結果は以下のようにまとめることが可能です．

\begin{align}
    C_u&=\max(S_0u-K, 0) \\
  C_d&=\max(S_0d-K, 0) \\
  x&=\frac{C_u-C_d}{S_0(u-d)} \\
  y&=\frac{uC_d-dC_u}{(1+r)(1-d)}\\
  C&=\frac{1}{1+r}\left\{\frac{(1+r)-d}{u-d}C_u+\frac{u-(1+r)}{u-d}C_d\right\}
\end{align}

ただし，ここでは$S_u=S_0u, S_d=S_0d,u > d$とおきました．
また，$C_u, C_d$は$t=T$でのオプションの価格を表しています．

ここで一つ気づくことは，オプションの価格が確率$p$よらないことです．一方で

   p^\ast = \frac{(1+r)-d}{u-d}\\ 
   q^\ast = \frac{u-(1+r)}{u-d}

とおくと，$0\leq p^\ast,q^\ast\leq 1, p^\ast+q^\ast=1$であり，$p^\ast, q^\ast$は確率とみなすことができます．
この$p^\ast, q^\ast$はリスク中立確率と呼ばれます．
これをつかうと

$$
C=\frac{1}{1+r}\left(p^\ast C_u+q^\ast C_d\right)
$$

と書くことができます．この結果を改めて解釈すると，オプションの価格は確率$p^\ast, q^\ast$のもとでの$t=T$におけるオプション価格$C(T)={C_u, C_d}$の期待値を現在価値に割り引いたものとみなすことができます．

一期間二項モデルについて，オプションと同じキャッシュフローを持つポートフォリオを作成することで，オプションの価格決定を行うことができました．この結果は$m$期間$n$項モデルにも拡張可能です．

連続型確率過程のもとでのオプションの価格決定

さて，ここまで考えてきた一期間二項モデルは現実とは程遠いモデルなので，もう少し現実の価格変動に近い確率過程を考えてみます．

デリバティブの価格決定問題では価格変動のモデルに幾何ブラウン運動などがよく用いられます．

幾何ブラウン運動のサンプルパスは上図のようになります．

一期間二項モデルは時刻は2時点のみで$T$時点でのとりうる資産価格は2つしかありません．
対して幾何ブラウン運動は$t \in [0, T]$の連続時間確率過程となっており，とりうる資産価格は連続量になっています．

ここでは連続時間確率過程を使って資産価格の変動をモデル化します．

連続時間確率過程においては，ヨーロピアンコールオプションの価格は

$$
C=e^{-rT}E_Q\left[f(S(T))|S(0)=S_0\right]
$$

と書くことができます．ここで$E_Q\left[\cdot|S(0)=S_0\right]$はリスク中立確率(測度)のもとでの条件付期待値を表し，$f(S(T))=\max(S(T)-K, 0)$は満期時点でのオプション価格を表します．$e^{-rT}$は割引のファクターで，一期間二項モデルの$\frac{1}{1+r}$に対応しています．

多少表記がややこしくなりましたが，やることは一緒で，リスク中立確率のもとで満期時点でのオプション価格の期待値を計算すれば良いということです．

幾何ブラウン運動の場合には解析解が知られています(Black-Scholesモデル)．
しかしながら，一般の連続型確率過程については数値計算によりこの期待値を求める必要があります．

数値計算による方法としてはツリー法²や，モンテカルロ法が挙げられます．

3. モンテカルロ法

ここでは最もよく使われるモンテカルロ法を紹介します．

ここでは$t=T$での資産価格のリスク中立確率測度下での確率分布が既知であるとします．
特に，幾何ブラウン運動の場合には

$$
S(T) = S_0\exp\left[\left(r-\frac{\sigma^2}{2}\right)T+\sigma\sqrt{T}W\right]
$$

となることが知られています．ここで$r$は金利，$\sigma$は幾何ブラウン運動の標準偏差，$W$は標準正規分布に従う確率変数です．

モンテカルロ法による期待値計算では積分をする代わりに確率分布に従う乱数を発生させ，積分を標本平均で近似します．

ここではヨーロピアンコールオプションの価格決定をモンテカルロ法で行う手順を紹介します．
1. 以下の2から4をN回繰り返す
2. 標準正規分布に従う乱数を発生させて$W_i$とする
3. $S_i=S_0\exp\left[\left(r-\frac{\sigma^2}{2}\right)T+\sigma\sqrt{T}W_i\right]$を計算する
4. $f(S_i)=\max\left[S_i-K, 0\right]$を計算する
5. N個のサンプルが得られるので，$E_Q\left[f(S(T))|S(0)=S_0\right]\cong \frac{1}{N}\sum_{i=1}^Nf(S_i)$として近似する

さて，自分の欲しい精度で価格決定を行いたい場合に必要な$N$を見積もりたいと思います．
ここで$X=f(S(T))$とおきます．標本平均$\frac{1}{N}\sum_{i=1}^NX_i$の分散を考えると

\begin{align}
  V\left[\frac{1}{N}\sum_{i=1}^NX_i\right]&=\frac{1}{N^2}\sum_{i=1}^NV[X_i]\\
  &=\frac{\sigma^2}{N}
\end{align}

したがって標本平均の標準偏差$\epsilon$は$O(1/\sqrt{N})$で減少することがわかります．
逆に言うと欲しい精度$\epsilon$があった場合$N=O(1/\epsilon^2)$だけ繰り返せばいいという事がわかります．

4. 量子アルゴリズム

やっと本題に入ります．

ここでは量子アルゴリズムを用いてヨーロピアンオプションの価格決定を行います．
モンテカルロ法によるオプションの価格を$\epsilon$の精度(標準偏差)で得たい場合には$N=O(1/\epsilon^2)$のサンプルが必要になるのでした．

量子アルゴリズムをもちいることでこれが$N=(1/\epsilon)$に減らせます

これを見ていきましょう．
大まかに言うとオプション価格計算に必要なのは次の2ステップです
1. Distribution Loading: $\sum_{j=0}^{2^n-1}\sqrt{p_j}\left| j \right>$を作ります．ここで$n$は量子ビット数で，${p_i}, (i=0,1,\dots,2^n-1)$は確率密度関数$p(x)$を離散化したものです．
2. Quantum Amplitude Estimation³: $N=O(1/\epsilon)$で期待値を計算します．

これらを詳しく説明したいと思います．
その前に，これらのステップに必要なモジュールを用意していきたいと思います．

Quantum Arithmetics

量子回路を用いた算術演算をQuantum Arithmeticsと呼んでいます．
これは既知の関数$f$に対して

$$
\left| x \right> \rightarrow \left| f(x) \right>
$$

を行う回路です．
重ね合わせられた状態に対しては

$$
\sum_i\left| x_i \right> \rightarrow \sum_i\left| f(x_i) \right>
$$

となります．

Quantum Phase Estimation

ユニタリ演算子$U$に対し，その固有値は$e^{i\theta}$という形で表されます．
この$U$と，固有値$e^{i\theta}$に対応する固有状態$\left| \psi \right>$に対して

$$
\left| \psi \right> \stackrel{QPE}{\rightarrow} \left| \psi \right>\left| \theta \right>
$$

という形で固有値の位相を取り出すことができます．
詳細はNielsen Chuang等を参照してください．

Distribution Loading

まず，仮定として任意の$a\leq b=0,\dots2^{n-1}$に対して，

$$
\sum_{j=a}^{b}p_j\cong\int_{x_a}^{x_b}p(x)dx
$$

が古典で効率よく計算できるとします．
計算できる，というだけで$2^n$個全てについて計算するわけではないことに注意します．例えば幾何ブラウン運動などではこれが満たされています．

ここで，$m=1,\dots,n; k=0,\dots,2^{m-1}$に対して$p_k^{(m)}$を

$$
p_k^{(m)}=\sum_{j=k2^{n-m}}^{(k+1)2^{n-m}-1}p_j
$$

と定義します．
ややこしいので，いくつかの$m,k$について見てみます．

• $m=1, k=0$で$p_0^{(1)}=\sum_{j=0}^{2^{n-1}-1}p_j$
• $m=2, k=0$で$p_0^{(2)}=\sum_{j=0}^{2^{n-2}-1}p_j$
• $m=2, k=1$で$p_0^{(2)}=\sum_{j=2^{n-2}}^{2^{n-1}-1}p_j$

$m=1$では$2^{n-1}$個の和ですが，$m=2$では$k=0$と$k=1$で$2^{n-2}$個ずつの和に分けられます．

$m=n$では$p_k^{(n)}=p_k$となります．

ここで，$\left| \psi^{(m)} \right>$を

$$
\left| \psi^{(m)} \right>=\sum_{k=0}^{2^m-1}\sqrt{p_k^{(m)}}\left| k \right>
$$

と定義します．

このとき$\left| \psi^{(m)} \right>$から$\left| \psi^{(m+1)} \right>$を計算できれば$m=n$まで計算して

$$
\left| \psi^{(n)} \right> = \sum_{k=0}^{2^n-1}\sqrt{p_k^{(n)}}\left| k \right> = \sum_{k=0}^{2^n-1}\sqrt{p_k}\left| k \right>
$$

となり，所望の状態が得られます．

では，$\left| \psi^{(m)} \right>$から$\left| \psi^{(m+1)} \right>$を計算してみましょう．

まず，$\sum_{j=a}^{b}p_j$が効率よく計算できるので，古典で
$$
\cos^{-1}\sqrt{\frac{p^{(m+1)}}{p_k^{(m)}}}
$$
が計算可能です．そうするとquantum arithmeticによって

$$
\left| \psi^{(m)} \right> \rightarrow \left| \psi^{(m)} \right>\left| \cos^{-1}\sqrt{\frac{p^{(m+1)}}{p_k^{(m)}}} \right>
$$

を用意します．
rotationを使って

$$
\left| \psi^{(m)} \right>\left| \cos^{-1}\sqrt{\frac{p^{(m+1)}}{p_k^{(m)}}} \right> \rightarrow \left| \psi^{(m)} \right> \left(\sqrt{\frac{p^{(m+1)}}{p_k^{(m)}}}\left| 0 \right> + \sqrt{1-\frac{p^{(m+1)}}{p_k^{(m)}}} \left| 1 \right>\right)
$$

とします．これは

$$
\left| \psi^{(m)} \right> \left(\sqrt{\frac{p^{(m+1)}}{p_k^{(m)}}}\left| 0 \right> + \sqrt{1-\frac{p^{(m+1)}}{p_k^{(m)}}} \left| 1 \right>\right)=
\sum_{k=0}^{2^m-1}\left(\sqrt{p_{2k}^{(m)}}\left|k\right>\left|0\right>+\sqrt{p_{k}^{(m)}-p_{2k}^{(m+1)}}\left|k\right>\left|1\right>\right) = \left|\psi^{(m+1)}\right>
$$

となり，$\left|\psi^{(m+1)}\right>$が得られます．
これで$\left|\psi^{(m)}\right>$から$\left|\psi^{(m+1)}\right>$を得られるので，順に$m=n$まで計算していけば，ほしかった状態$\sum_{k=0}^{2^n-1}\sqrt{p_k}\left| k \right>$が得られます．

Quantum Amplitude Estimation

Distribution Loadingで$\sum_{k=0}^{2^n-1}\sqrt{p_k}\left| k \right>$が得られたので，期待値計算を考えてみます．

まずはQuantum Amplitude Estimationを使わずに期待値計算をしてみます．
rotationを使って

$$
\sum_{k=0}^{2^n-1}\sqrt{p_k}\left| k \right> \rightarrow \sum_{k=0}^{2^n-1}\sqrt{p_k}\left| k \right>\left(\sqrt{1-v(k)}\left| 0 \right>+\sqrt{v(k)}\left| 1 \right>\right):=\left| \chi \right>
$$

を得ます．補助量子ビットの$\left| 1 \right>$を測定することで

$$
\mu=\left< \chi \right|I^{\otimes n}\otimes\left| 1 \right>\left< 1 \right.\left| \chi \right>=\sum_{k=0}^{2^n-1}p_kv(k)
$$
となり，期待値を計算することができます．

このとき，必要な測定回数を考えてみます．
平均が$\mu$の二項分布では$N$回サンプルした場合の標本分散が$\epsilon^2=\frac{\mu(1-\mu)}{N}$であるので，精度$\epsilon$が必要な場合には$N=O(1/\epsilon^2)$が必要になります．
これだと古典でのモンテカルロ法と変わらない，という結果になります．

そこで，量子加速を得るためにQuantum Amplitude Estimation (QAE)を用いることにします．

QAEではある回転行列を構成します．
回転行列の固有値がその回転角$\theta$を用いて$e^{\pm i\theta}$となるので，Quantum Phase Estimationを用いて$\theta$を取り出し，$\mu=\frac{1}{2}(1-\cos\theta/2)$から期待値を計算することができます．

以下でQAEの手順を見ていきたいと思います．
まず，

$$
V=I^{\otimes n+1}-2I^{\otimes n}\otimes\left| 1 \right>\left< 1 \right|
$$

というユニタリ演算子を用意します．
この演算子$V$の$\left| \chi \right>$での期待値で考えると

$$
\left< \chi \right|V\left| \chi \right>=1-2\mu
$$

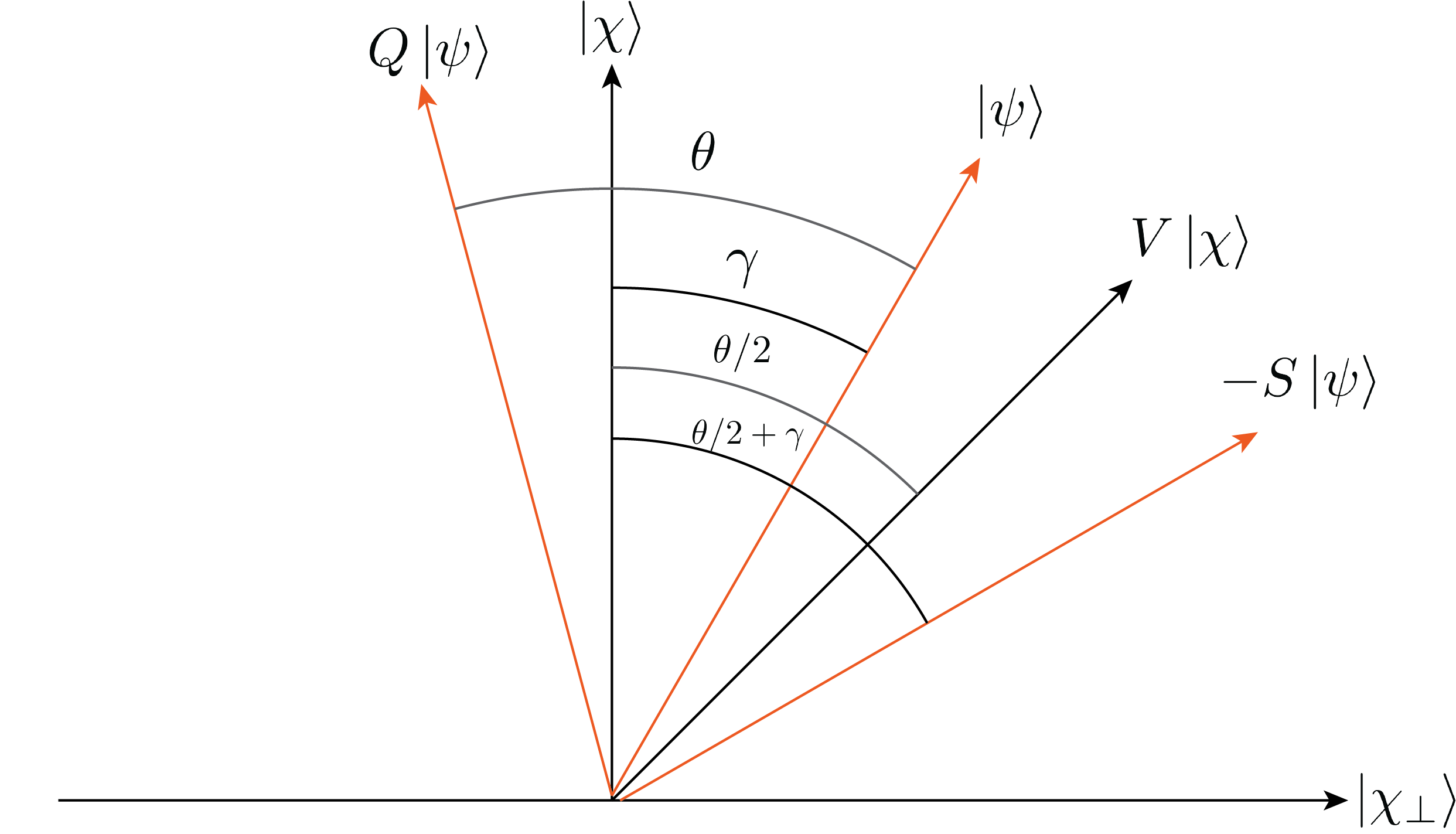
一方で，$V$を$\left| \chi \right>$に作用させると，$\left| \chi \right>$とそれに直交する$\left| \chi_\perp \right>$の線形結合でかけます．これを

$$
V\left| \chi \right>=\cos(\theta/2)\left| \chi \right>+e^{i\phi}\sin(\theta/2)\left| \chi_\perp \right>
$$

と表現すると，

$$
1-2\mu=\cos(\theta/2)
$$

であるから，$\mu$を求める代わりに$\theta$を計算する問題に置き換えることができます．

また，$V\left| \chi \right>$は$\left| \chi \right>$と$\left| \chi_\perp \right>$で張られる二次元平面内で$\left| \chi \right>$を$\theta/2$だけ回転させたものとみなすことができます．

さらに

$$
U=I^{\otimes n+1}-2\otimes \left| \chi \right>\left< \chi \right|
$$

$$
S=I^{\otimes n+1}-2\otimes V\left| \chi \right>\left< \chi \right|V
$$

というユニタリ演算子を定義します．$-U$は，$\left| \chi \right>$と$\left| \chi_\perp \right>$で張られる二次元平面内のあるベクトル$\left| \psi \right>$を$\left| \chi \right>$に関して対称なベクトルに写す操作に対応しており，
$-S$は$\left| \psi \right>$を$V\left| \chi \right>$に関して対称なベクトルに写す操作に対応しています．

ここで，

$$
Q=US
$$

と定義すると，この$Q$は$V\left| \chi \right>$は$\left| \chi \right>$と$\left| \chi_\perp \right>$で張られる二次元平面内で$\left| \psi \right>$を$\theta$だけ回転させる操作となります．

回転角$\theta$をもつ回転行列の固有値は$e^{\pm i\theta}$であるので，QPEを用いてこの回転行列の固有値を推定することができれば，期待値$\mu$を計算できます．

では計算のステップ数はどの程度になるでしょうか？

実はQAEを用いて$U,V$を$O(N\log(1/\delta))$回作用させたとき，$\mu$の推定値$\hat{\mu}$の推定誤差が

$$
|\hat{\mu}-\mu| \leq C\left(\frac{\sqrt{\mu}}{N}+\frac{1}{N^2}\right)
$$

となる確率の下限が$1-\delta$であることが知られています．
$\delta$を固定してやったとき，ほしい精度$\epsilon$に対して
$|\hat{\mu}-\mu|\leq\epsilon=O(1/N)$という評価ができるので

$$
N=O\left(\frac{1}{\epsilon}\right)
$$

が得られることになります．

これでQAEを用いることでヨーロピアンオプションの価格計算に必要な計算ステップ数が

$$
O\left(\frac{1}{\epsilon^2}\right)\rightarrow O\left(\frac{1}{\epsilon}\right)
$$

となることがわかりました．

まとめと展望

本稿では金融派生商品であるデリバティブを紹介し，特にデリバティブの中でもヨーロピアンオプションの価格計算について紹介しました．古典の数値計算手法としてはモンテカルロ法を紹介しました．
さらに，量子振幅推定を用いることでヨーロピアンオプションの価格決定問題に対して2次加速が得られることを示しました．

Distribution loadingに関してはquantum arithmeticsを最適化する方法⁴や，qGANを用いる方法⁵が提案されています．
また，QAEをQPEなしで行う方法⁶も提案されています．
本稿で紹介したアルゴリズムは量子回路のサイズがかなり大きくなってしまうので，これらの提案を用いることで少しでも回路を減らしていこうという試みがなされています．

間違い等あれば是非コメントお待ちしております．

---

1. P. Rebentrost, B. Gupt, and T. R. Bromley, “Quantum computational finance: Monte Carlo pricing of financial derivatives,” Phys. Rev. A, vol. 98, no. 2, pp. 1–15, 2018. ↩

2. J. C. Cox, S. A. Ross, and M. Rubinstein, “Option pricing: A simplified approach,” J. financ. econ., vol. 7, no. 3, pp. 229–263, 1979. ↩

3. G. Brassard, P. Høyer, M. Mosca, and A. Tapp, “Quantum amplitude amplification and estimation,” pp. 53–74, 2002. ↩

4. Y. R. Sanders, G. H. Low, A. Scherer, and D. W. Berry, “Black-Box Quantum State Preparation without Arithmetic,” Phys. Rev. Lett., vol. 122, no. 2, Jul. 2019. ↩

5. C. Zoufal, A. Lucchi, and S. Woerner, “Quantum Generative Adversarial Networks for Learning and Loading Random Distributions,” pp. 1–14, 2019. ↩

6. Y. Suzuki, S. Uno, R. Raymond, T. Tanaka, T. Onodera, and N. Yamamoto, “Amplitude Estimation without Phase Estimation,” Apr. 2019. ↩