ドローン動力学の数学と実装

ドローン動力学の数学とC++ライブラリ

これは何？

地上と機体座標系間の変換や，ロータの推力と重力からドローンの速度，加速度などが計算できるC++ライブラリを作成しました．その時に書いた数式を解説します．

写真は Ryze Tech Tello

当初この箱庭 PX4 ドローンシミュレーションプロジェクト用に開発されましたが，その中から汎用的に利用できる部分を切り出し，さらに，インターフェイスをより使いやすくし，以下の参考文献との対応をとって公開することにしました．

すべての関数は，以下の書籍の式の C++ 実装であり，ソースコードコメントにも式番号が記載されています．本のすべての式を実装しているわけではありませんが，箱庭プロジェクトのドローンはこのライブラリを使って実際に飛行しています．なお，C 言語の I/F もあります．本文中の式番号は，この本の中の式番号です．

• 『ドローン工学入門』工学博士 野波健蔵【著】

この記事，および実装ライブラリは，箱庭プロジェクト（サイバーフィジカルシステムのシミュレーションのための，オープンソースランタイム環境）において，小型無人航空機（ドローン）プラントモデルのための，数学，物理，および動力学ライブラリとして開発されています．実装の詳しくは，

• https://github.com/toppers/hakoniwa-px4sim/drone_physics/

を参照してください．ここでは，数式を中心に解説します．ただし，数式の意味１つ１つについては，上記の本に譲って，この記事では，実際にテスト済みのC++関数として実装された数式を記述していくことによって，この分野の他の開発者の参照になることを目的にしています（ぜひソースコードも参照ください）．

数式

地上座標系は，右手系で定義されており， $z$ 軸は下向きです．機体座標系は，右手系で定義されており， $x$ 軸は機体の前方向， $y$ 軸は機体の右方向， $z$ 軸は機体の下方向です．

機体座標系の原点は機体の重心です．機体座標系は機体に固定されており，機体座標系は機体とともに移動します．

オイラー角は，地上座標系の座標軸を機体座標へと， $z$ -軸($\psi$)， $y$ -軸($\theta$)， $x$ -軸($\phi$)の順に回転することで重ねられるように表現するとします．

$\phi, \theta, \psi$ は，2つの座標系の橋渡しとなるものであり，両方の座標系で同じ値が使用されます．別の言い方をすると，オイラー角は地上座標系と機体座標系の方程式で同じです（一方から他方に変換されるものではありません）．

基本的な力学方程式は，機体座標系で以下のようになります eq.(2.31)．

$$
\begin{array}{l}
m \dot{v} + \omega \times m v = F \newline
I \dot{\omega} + \omega \times I \omega = \tau
\end{array}
$$

ここで，

• $m$ - 機体の質量
• $I$ - 機体の慣性行列
• $v$ - 機体の速度 $v=(u, v, w)^T$
• $\omega$ - 機体の角速度 $\omega = (p, q, r)^T$
• $F$ - 機体に働く力のベクトル．重力($mg$)，空気抵抗($-dv$)，推力($T$)からなる．
• $\tau$ - 機体に働くトルクのベクトル．ローターの推力によるものと，反トルクの合計ベクトル．

これらを，ドローンの力学に適用すると，以下のようになります．

機体座標系の動力学方程式

機体座標系の動力学方程式です．このライブラリでは基本的にこの方程式を後述の座標変換と合わせて使用することで，
全状態変数と力とトルクによる時間微分$(u,v,w,\dot{u},\dot{v},\dot{w},p,q,r,\dot{p},\dot{q},\dot{r})$ が計算できます．

最終的に，機体速度 $(u,v,w)^T$ を地上に変換して求めた $(u_e, v_e, w_e)^T$ を時間積分することで，機体の位置 $(x,y,z)^T$ が求まります．また，
機体角加速度 $(p,q,r)^T$ から後述の変換で求まるオイラー角変化率$(\dot{\phi}, \dot{\theta}, \dot{\psi})^T$ を時間積分することで，機体の姿勢 $(\phi, \theta, \psi)^T$ が求まります．

速度，加速度(並進)

$$
\begin{array}{l}
\dot{u} = -g \sin{\theta} -(qw -rv) -\frac{d}{m}u \newline
\dot{v} = g \cos{\theta}\sin{\phi} -(ru -pw) -\frac{d}{m}v \newline
\dot{w} = -\frac{T}{m} + g \cos{\theta}cos{\phi} -(pv-qu) -\frac{d}{m}w
\end{array}
$$

角速度，角加速度(回転)

$$
\begin{array}{l}
\dot{p} = (\tau_{\phi} -qr(I_{zz}-I_{yy}))/I_{xx} \newline
\dot{q} = (\tau_{\theta}-rp(I_{xx}-I_{zz}))/I_{yy} \newline
\dot{r} = (\tau_{\psi}-pq(I_{yy}-I_{xx}))/I_{zz}
\end{array}
$$

ここで，

• $m$ - 機体の質量($m>0$)
• $g$ - 重力加速度($g>0$)
• $(u, v, w)^T$ - 機体の速度(機体座標)
• $(p, q, r)^T$ - 機体の角速度(機体座標)
• $d$ - 並進に影響する空気抵抗($d>0$)
• $(\tau_\phi, \tau_\theta,\tau_\psi)^T$ - 機体に働くトルクのベクトル．ローターの推力の号力($\tau_\phi, \tau_\theta$)と，反トルク($\tau_\psi$)．
• $\phi, \theta, \psi$ は機体座標系のオイラー角．ロール($x$-軸)，ピッチ($y$-軸)，ヨー($z$-軸)角．
• $I_{xx}​,I_{yy}, I_{zz}$ は機体座標系の慣性モーメント（ $x, y, z$ 軸は機体の主軸に沿っており，他の慣性モーメント $I_{xy}, I_{yz}, I_{zx}$ はゼロとする）．

地上座標系の動力学方程式

地上座標系では並進についてのみ以下のように計算できます（すべて地上座標系を使った回転はイナーシャの時間変化等のため複雑になるので，等ライブラリでは扱わない）．

$$
\begin{array}{l}
\dot{u_e} = -\frac{T}{m}(\cos{\phi}\sin{\theta}\cos{\psi} + \sin{\psi}\sin{\phi}) - \frac{d}{m}u_e \newline
\dot{v_e} = -\frac{T}{m}(\cos{\phi}\sin{\theta}\sin{\phi} - \sin{\phi}\cos{\psi}) -\frac{d}{m}v_e \newline
\dot{w_e} = -\frac{T}{m}(\sin{\phi}\cos{\theta}) +g -\frac{d}{m}w_e
\end{array}
$$

座標変換

機体座標系と地上座標系の変換は以下のようになります．

速度，加速度の変換

機体座標系 $v = (u, v, w)^T$ から地上座標系 $v_e = (u_e, v_e, w_e)^T$ への変換行列は以下のようになります．加速度も同様です．

$$
\left[
\begin{array}{c}
u_e \newline
v_e \newline
w_e \end{array}
\right] =
\begin{bmatrix}
\cos\theta\cos\psi & \sin\phi\sin\theta\cos\psi - \cos\phi\sin\psi & \cos\phi\sin\theta\cos\psi + \sin\phi\sin\psi \newline
\cos\theta\sin\psi & \sin\phi\sin\theta\sin\psi + \cos\phi\cos\psi & \cos\phi\sin\theta\sin\psi -\sin\phi\cos\psi \newline
-\sin\theta & \sin\phi\cos\theta & \cos\phi\cos\theta
\end{bmatrix}
\left[
\begin{array}{c} u \newline
v \newline
w \end{array}
\right]
$$

角速度（回転）とオイラー角変化率の変換

機体座標系の角速度 $(p, q, r)^T$ からオイラー角変化率 $(\dot{\phi}, \dot{\theta}, \dot{\psi})^T$ への変換行列は以下のようになります．

$$
\begin{bmatrix}
\dot{\phi} \newline
\dot{\theta} \newline
\dot{\psi}
\end{bmatrix} =
\begin{bmatrix}
1 & \sin \phi \tan \theta & \cos \phi \tan \theta \newline
0 & \cos \phi & -\sin \phi \newline
0 & \sin \phi \sec \theta & \cos \phi \sec \theta
\end{bmatrix}
\begin{bmatrix}
p \newline
q \newline
r
\end{bmatrix}
$$

1つのローターの力学

1ロータの回転数（角速度）

1つ1つのモーターの角速度は， $\Omega(t)$ は，デューティー比 $d(t)$ によって1次遅れ系としてモデル化できます．
書籍の式 (2.48) の伝達関数 $G(s)$ によって記述され，

$G(s)= K_r/(T_r s + 1)$

時間領域の微分方程式（角速度の時間変化率）は以下のようになります．

$\dot{\Omega}(t) = (K_r d(t) - \Omega(t))/ T_r$

ここで，

• $K_r$ - ローターのゲイン定数
• $T_r$ - ローターの時定数
• $d(t)$ - ローターのデューティー比 ($0.0 \le d(t) \le 1.0$)

1つのロータ推力 $T$ は，ローターの角速度 $\Omega$ の2乗に比例します eq.(2.50)．
$A$ はローターのサイズと空気密度に関連するパラメータです．

1ローターのトルクと反トルク

$T = A \Omega^2 $

反トルク $\tau_i$ はとローターの角速度 $\Omega$ の関係式は以下のようになります eq.(2.56)．

$\tau_i = B \Omega^2 + Jr \dot{\Omega}$

ここで， $B$ と $Jr$ はローターの特性に関連するパラメータです．
これによって，機体は $z$ 軸周りに回転します．

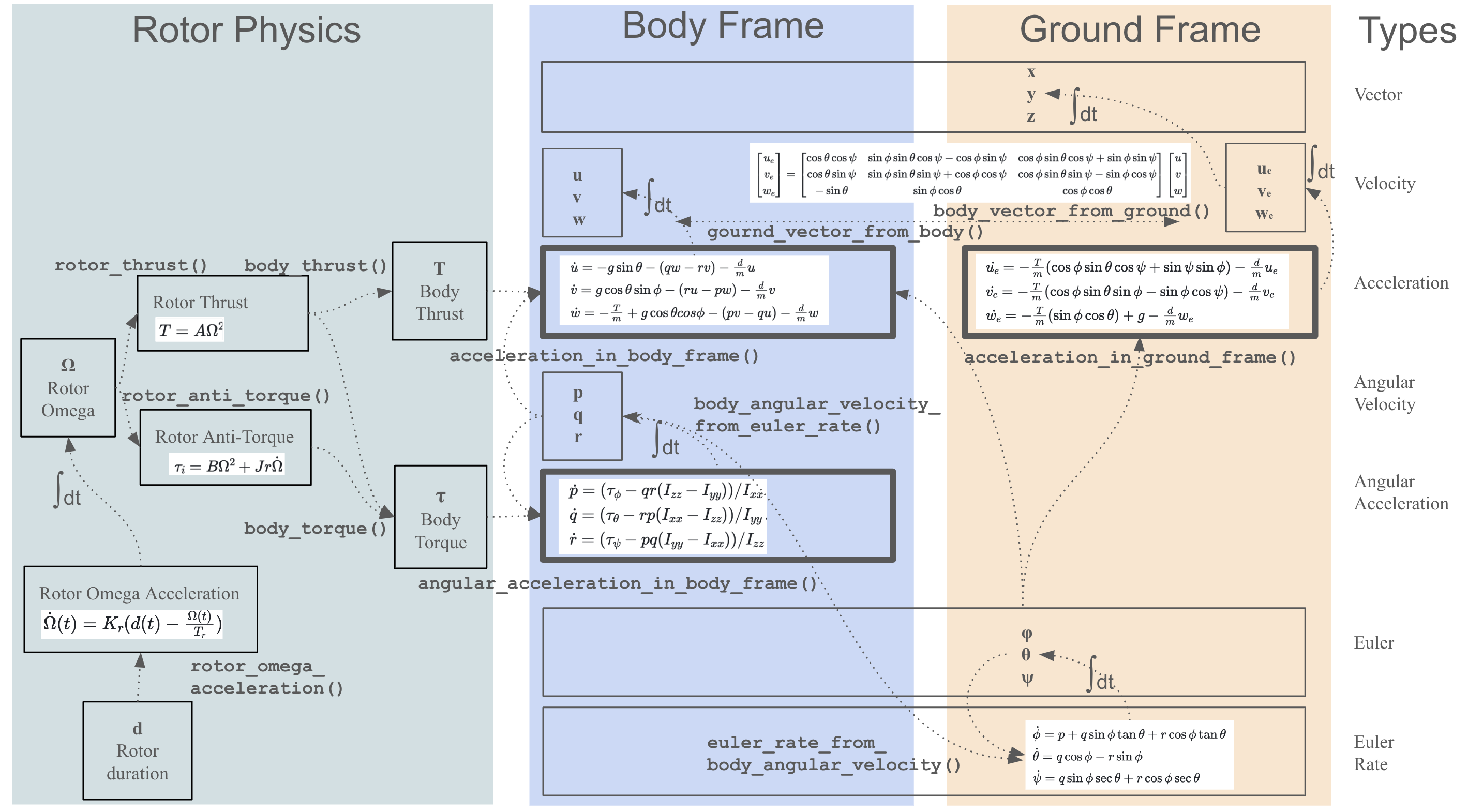
数式と関数の全体像

ここでは，状態変数，数式と関数の全体像を示します．機体の位置 $(x,y,z)^T$ と姿勢のオイラー角 $(\phi, \theta, \psi)^T$ はわかりやすいように地上側に配置しています（両者の架け橋です）．また，ここに登場していない関数も多数用意しています．

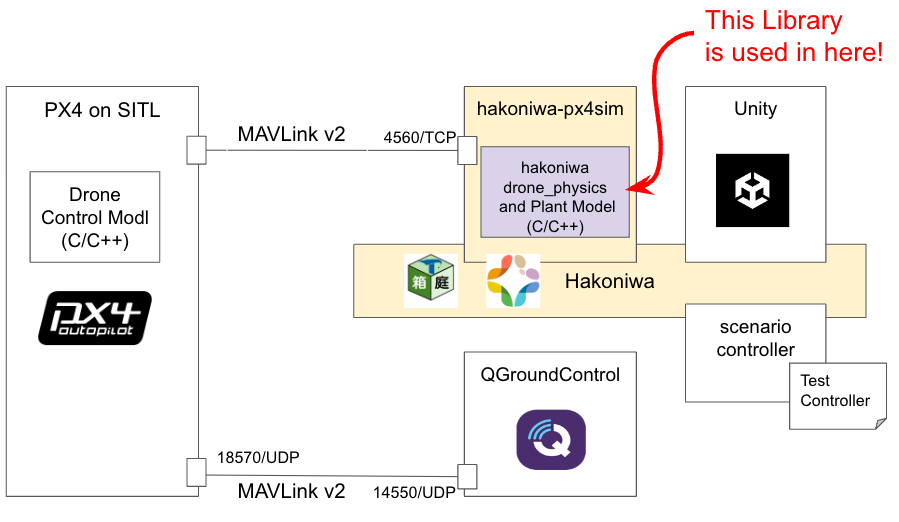
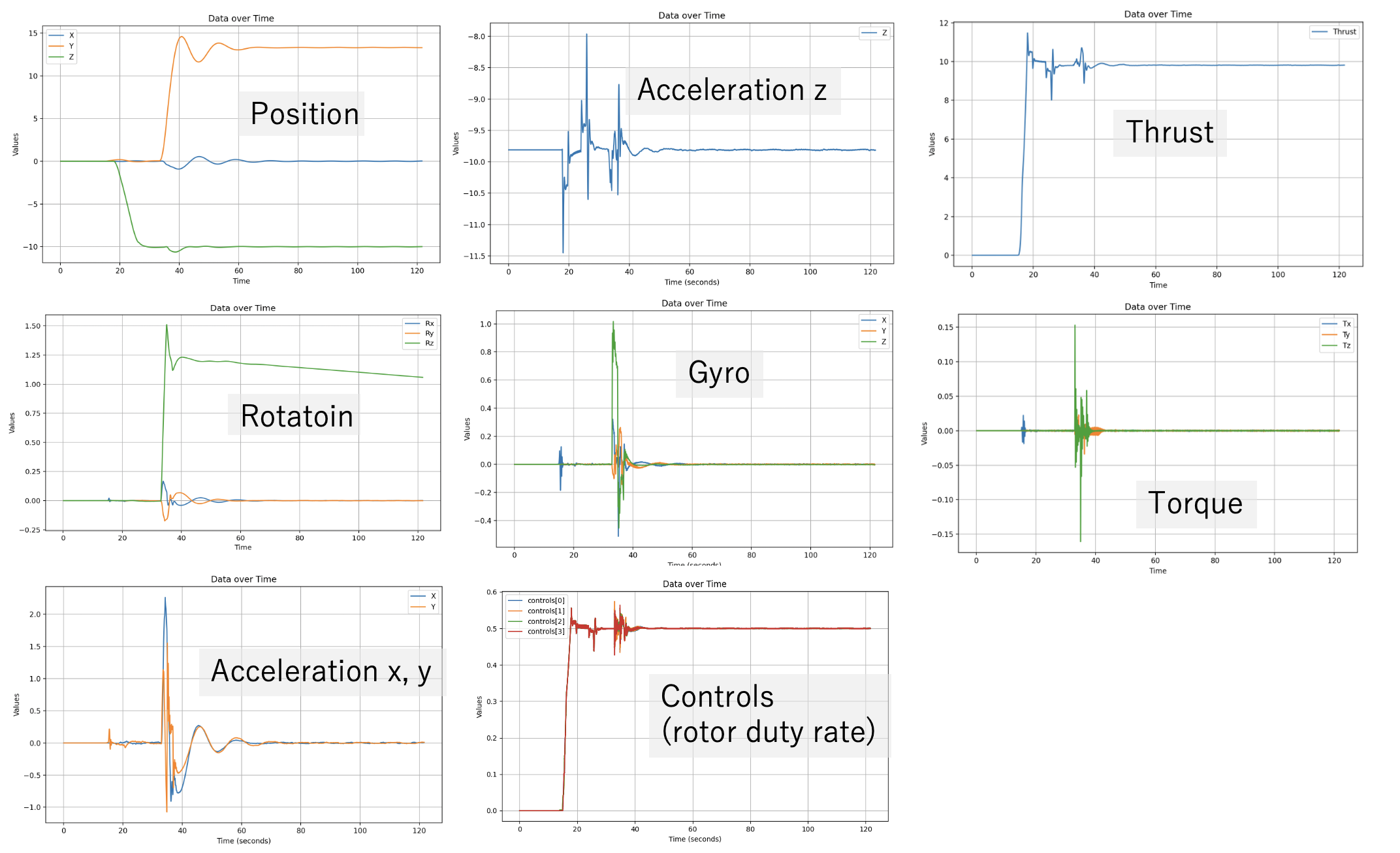
実験

私たちは，Hakoniwa を PX4 SITL シミュレータに接続し，ライブラリを以下の実験でテストしました．全体アーキテクチャはこのようなものです．

実験のミッション:

• 離陸し，高度10mでホバリングする．
• 右へ10m移動して停止する．

関数リスト

関数は以下のカテゴリから構成され，書籍の式番号が記載されています（C++）．

座標変換

関数	数式	意味
ground_vector_from_body	(1.71), (1.124)	機体座標のベクトルを地上座標に変換
body_vector_from_ground	(1.69), (1.124)の逆変換	地上座標のベクトルを機体座標に変換
euler_rate_from_body_angular_velocity	(1.109)	機体角速度をオイラー角の変化率に変換
body_angular_velocity_from_euler_rate	(1.106)	オイラー角の変化率を機体各速度に変換

機体の力学(力と加速度)

関数	数式	意味
acceleration_in_body_frame	(1.136),(2.31)	力による機体座標系での加速度計算
angular_acceleration_in_body_frame	(1.137),(2.31)	力による機体座標系での角加速度計算
acceleration_in_ground_frame	(2.46), (2.47)	力による地上座標系での加速度計算
euler_acceleration_in_ground_frame	(1.109)の微分	トルクによる地上座標系でのオイラー角2次変化率計算

1ロータの力学（回転数と推力）

関数	数式	意味
rotor_omega_acceleration	(2.48)	ローター角速度の加速度計算
rotor_thrust	(2.50)	ローター推力計算（機体 $z$ 軸のマイナス方向）
rotor_anti_torque	(2.56)	ローターの反トルク計算（機体 $z$ 軸周り回転

n 個のローターによる機体力学（機体の推力とトルク）

関数	数式	意味
body_thrust	(2.61)	$n$ 個のローターの推力の合力
body_torque	(2.60)-(2.62)	$n$ 個のローターのトルクの合力．ローターの設置位置も関係する．

Hello World

C++では，

#include <iostream>

// include the library header
#include "drone_physics.hpp"

int main() {
    // このライブラリの名前空間
    using namespace hako::drone_physics;

    // 機体座標系を Euler 角で指定
    VectorType frame = {0, 0, M_PI/2};
    VelocityType body_velocity = {100, 200, 300};
    
    // 機体座標系から地上座標系への速度変換
    VelocityType ground_velocity = ground_vector_from_body(body_velocity, frame);

    // x,y,z 座標を取り出す
    auto [u, v, w] = ground_velocity;

    std::cout << "u = " << u << ", v = " << v << ", w = " << w << std::endl;
    // output: u = 200, v = -100, w = 300

    // 逆変換して戻す
    VelocityType body_velocity2 = body_vector_from_ground(
        {u, v, w},
        {0, 0, M_PI/2}
    );

    auto [u2, v2, w2] = body_velocity2;
    std::cout << "u2 = " << u2 << ", v2 = " << v2 << ", w2 = " << w2 << std::endl;
    // output: u2 = 100, v2 = 200, w2 = 300, back again.
}

C言語では，

#include <stdio.h>

// include the library header
#include "drone_physics_c.h"

int main() {
    // 機体座標系を Euler 角で指定, dp_ は dron_physics の接頭
    dp_euler_t frame = {0, 0, M_PI/2};
    dp_velocity_t body_velocity = {100, 200, 300};

    // 機体座標系から地上座標系への速度変換
    dp_velocity_t g = dp_ground_vector_from_body(&body_velocity, &frame);

    // x,y,z 座標を取り出す
    printf("x=%g, y=%g, z=%g\n", g.x, g.y, g.z);
    // output: u = 200, v = -100, w = 300

    // このように，初期化指定を使うこともできる
    // 逆変換して戻す
    dp_velocity_t b = dp_body_vector_from_ground(
        &g, &(dp_euler_t){0, 0, M_PI/2}
    );

    printf("x=%g, y=%g, z=%g\n", b.x, b.y, b.z);
    // output: x = 100, y = 200, z = 300, back again.

}

インストール

ソースコードをディレクトリごとコピーしてください．
CMkakeLists.txt があるので，CMake でビルドしてください．

$ cmake .
$ make

C++ ライブラリが，libdrone_physics.a として生成されます．
C言語ライブラリが，libdrone_physics_c.a として生成されます．
テストプログラムが，utest ctest examples cexamplesとして生成されます．

あなたのプログラム中で，このライブラリを使うには，

• C++言語では，あなたのプログラムに，drone_physics.hpp をインクルードし，libdrone_physics.a をリンクしてください．
• C言語では，あなたのプログラムに，drone_physics_c.hをインクルードし，libdrone_physics_c.a をリンクしてください．

examples.cpp と utest.cpp にC++言語での呼び出し例があります．
cexamples.c と ctest.c にC言語での呼び出し例があります．

型リスト

ベクトル

VectorType は，3次元のベクトル(座標値)です．機体座標系と地上座標系の両方で使用されます．以下のサブタイプがあります．

• VelocityType - 速度
• AccelerationType - 加速度
• ForceType - 力
• TorqueType - トルク

角速度ベクトル

• AngularVelocityType - 角速度
• AngularAccelerationType - 角加速度

オイラー角

EulerType は，3次元のオイラー角です．地上座標系から機体座標系への変換として使用されます．オイラー角はベクトルではありません．ベクトルのように加算・スカラー倍・行列演算することはできません．以下のサブタイプがあります．

• EulerType - オイラー角
• EulerRateType - オイラー角の変化率
• EulerAccelerationType - オイラー角の2次変化率

謝辞

難しい数学と力学について，非常に丁寧な解説書を書いていただいた，野波先生に感謝します．また，箱庭プロジェクトをリードし，実際に PX4, QGroundControl と接続し，長い時間を掛けて Unity でビジュアル表示しながら仮想的にドローンの飛行テストを行ってくれた，箱庭ラボの森さん（@tmori）に感謝します！

参考文献

特によく参照した文献は以下の通りです．コードの中にもリンクを埋め込んでいます．

• ドローン工学入門（野波健蔵博士）
• 小型無人航空機の厳密・簡易なモデリングとモデルベース制御（野波健蔵博士）
• Drone control Lecture(Seongheon Lee)
• 剛体の回転運動を支配するオイラーの運動方程式（スカイ技術研究所ブログ）
• オイラー角とは？定義と性質、回転行列・角速度ベクトルとの関係（スカイ技術研究所ブログ）
• 飛行力学における機体座標系の定義(@mtk_birdman)
• 「マルチコプタの運動と制御」基礎のきそ（伊藤恒平）

多くの書籍やWebコンテンツで勉強し，触発されています．ありがとうございます！