線形代数における行列変形と群の作用による理解

これは何？

大学の教養で学ぶ線形代数には、さまざまな概念や操作が出てきます。ここでは、主な「行列」の変形についてその変形前と変形後の特徴から、「不変量」と「標準形」に注目して統一的に解釈してみます。

動機は、「群と作用」について勉強したら、急に目の前が拓けたので、それを自分が得意な線形代数の中のテーマで書き出し、まとめてみたかったことです。

同値関係と同値類、不変量と標準形

実は、群の作用によって移り合う行列同士は、「同値関係」とそれが作る「同値類」に属することになります。同値関係は交わることなく集合を同値類にグルーピングするので、そのグルーピング観点を同値関係として理解できることになります。例えば、連立方程式を掃き出し法（消去法）によって解くときは行基本変形を使いますが、この変形操作で順々に変形されていく過程では、行列のランクや零空間は変化しません。つまり、１つの行列が同じ同値類（グループ）に存在しながら変化していくわけです（これを軌道といいます）。

2つの元が同じ同値類に含まれているかはどうやったらわかるでしょう？

その同値類ごとに「不変量」が分かれば、それを計算することで二つの元が同じ同値類かどうかテストできるようになります（テストは完全ではないかもしれません）。

もう一つの判別法は、その同値類ごとの代表元（「標準形」）を見つけることです。変形によって「標準形」にたどりつければ、2つの元が同じ同値類に含まれていることが分かります。標準形が一意に決まればですが（カノニカルな標準形）。

これらを維持する行列の変形を、群の作用によって書き出してみました。みなさんがよく知っている行列変形を「こんな群がこんなふうに作用している」と見えると目の前が開けますよ。

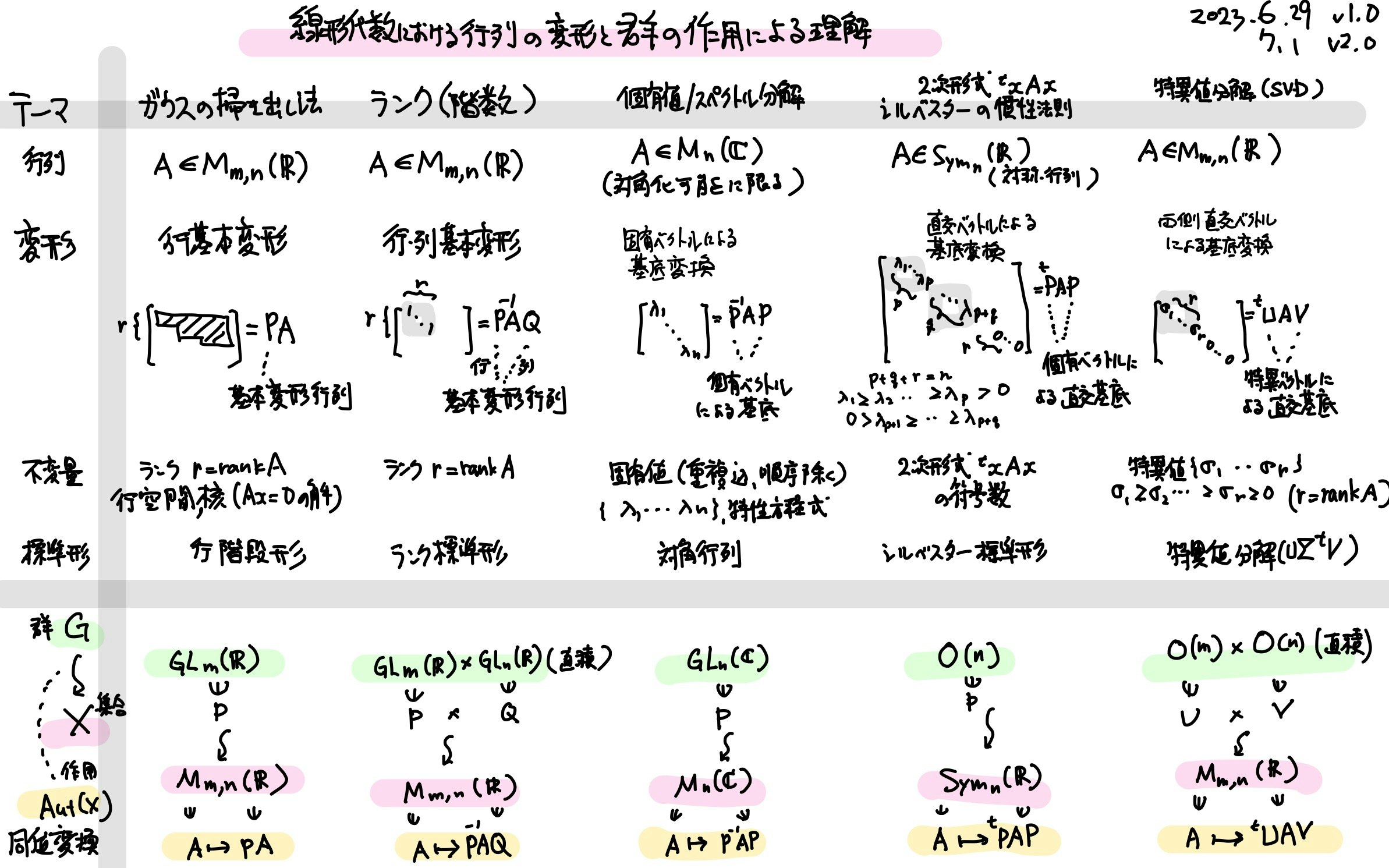
さっそくまとめ

線形代数側の記号として、行列 $A$ が 実数を要素とする $(m \times n)$ 行列の時、$A \in M_{m,n}(\mathbb{R})$、$n$次正方行列のとき、$A \in M_n(\mathbb{R})$、$n$次対称行列のとき、$A \in Sym_n(\mathbb{R})$ などと書きます。基礎体は $\mathbb{R}$ もしくは $\mathbb{C}$ を選んでいます。

群（としての線形代数）の記号として、$GL_n(\mathbb{R})$（一般線形群）, $O(n)$（$n$次直交群）などを使います。

上下段に分けて、主に次のことに言及しています。

• 上段に「線形代数」の目線でいくつかのテーマを取り出しています。
• 下段に「群の作用」と捉えたときの、群の名称、それらの具体的な作用（同値変換）

を書き出しました。群には必ず逆元が存在する（すなわち逆作用が存在する）ので、この作用は双方向で移り合います（同値関係を作る）。具体的な作用の形式は最下段です。

注目したテーマ

ガウスの掃き出し法（消去法）

ご存知、連立方程式を解く方法としてもよく知られる階段行列化です。前進消去の過程で現れます。この変形は、行基本変形を行列に左からどんどん掛けていくと見て、この操作を群 $GL_n(\mathbb{R})$ が $M_{m,n}(\mathbb{R})$ へ作用していると見ています。元のレベルでは、$GL_n(\mathbb{R})$ 元の$P$（基本変形行列） が $M_{m,n}(\mathbb{R})$ の元 $A$ に作用します。その軌道の中に行階段行列がある、ということです（ただし、ここでの標準形は唯一の代表元にはなりきれていない）。

また、この変形では、$A$のランク、行空間、零空間（$A$倍変換の核空間）が変化しません。よって、連立一次方程式$Ax=b$ の解に使える変形になっています。つまり連立一次方程式の解が同じ、というのがここで注目している同値関係ということになります。

$\mathbb{R}^m$側の基底を変更して、$\mathbb{R^m}$ベクトルの$A$倍変換$Ax$がをシンプルな形になるように表現行列を変えている。

と見ることができます。

ランク（階数）

行基本変形だけでなく、列基本変形も使えば、要素が0と1のみからなり「1が左上対角に要素にならんで残りは０」という行列にまで簡略化することができます。これを「階数標準形」（斎藤の用語）といいます。今度は、$\mathbb{R}^n$ と
$\mathbb{R}^m$の両方の空間の基底を取り替えているということになります（行空間も零空間も変化しますので、そののまま連立方程式の解には使えません）。その代わり、綺麗に1が並んでランク数を示す行列を標準形にとして作ることができます。また、この標準形はカノニカルな標準形です。

この場合、群の表現では、左と右の変形両方の群がセットで欲しくなります。よって、$G = GL_m(\mathbb{R}) \times GL_n(\mathbb{R})$ と直積で両側をペアにした群を作っています。そして、左側はわざと $P^{-1}$ と逆行列をとっています。これによって、$G$ が作用としての条件（結合法則）を満たせるようになります。

固有値（スペクトル分解）

線形代数のハイライトとも言える、正方行列の対角化、もしくはジョルダン分解です。ただし、ここでは対角可能な行列$A$に限って議論しています。

今度は、正方行列（自己準同型）が$A$の対象です。両側に別々の基底をとるのではなく１セットで共通基底を考えます。なので、より変形の自由度が厳しくなります。

この変形で結ばれる同値関係を「相似」とうことが多いと思います。

ここでの不変量は、（多重度を込めて$n$個の)固有値の列（順序は無視）です。特性方程式が不変量、と言うことも可能です（そこから、固有値やトレースも不変量であることが分かります）。

なお、ここでは対角化可能な場合に限定しましたが、そうでない場合も有名な「ジョルダン標準形」がこの同値類のカノニカルな標準形となります（他にも有理標準形など別のカノニカルな標準形も存在します）。

また、この固有値問題で複素数体（$M_n(\mathbb{C})$上の行列を選んだのは、実数の範囲では固有値が$n$個求まらない場合でも、複素数体で扱うことによって必ず$n$個の固有値が求まることで議論を簡略化できるからです。

2次形式（シルベスターの慣性法則）

$ax^2 + 2bxy + cy^2 = 0$ という実数係数の2次曲線分類問題から出発した問題です。この問題は、$^t xAx$ という2次形式を考えると、$A$ は実数の対称行列に限定して表現できることが分かります。実対称行列には、

実対称行列は、必ず直交行列によって実固有値の対角行列に相似変形できる

という大きな特徴があります。

よって、群は$O(n)$ $n$次直交群をとることができ、それを両側から掛ける変換が作用です。左側は転置（すなわち逆行列）を掛けることになります。

特異値分解（SVD）

特異値分解は、ランク不変同様 $\mathbb{R}^n$ （右側）と$\mathbb{R}^m$ 側（左側）の両方独立に基底を作ります。
しかし、この基底には大きな制約「正規直行基底」が課せられます。この基底が特異ベクトル（右、左）であり、変換後の行列の対角要素に現れるのが特異値です。

この強い制約のおかげで、標準形が（正負ペアを除いて）一意に決まります。また、固有値と違い、実数体の範囲内に閉じて標準形を作ることができます。作用する群としては、 $G = O(m) \times O(n)$（直積）です。

さらに、実数成分の特異値分解は、$^t AA$ の固有値問題に書き直せます。「正定値対称行列」の固有値問題では、前述のシルベスター標準において、負の係数が出てきません。それらの固有値の平方根が特異値になります。

つまり、すべての特異値は正値であり、これを大きい順序に並べれば、それが不変量となり、対角要素とすればカノニカルな標準形になります。

まとめ

ここでは、2つの大局的な視点を持ち出して、線形代数の複数のテーマを統一的に見てみました。

1. 同値、不変量、標準形
   変換で移り合うものを「同値」としたときの「同値類」の中で、一意ですっきりした代表元を「標準形」として見つけたい、というモチベーション、さらに、それらを $A$ を列ベクトルの線形変換 $Hom_k(\mathbb{R}^n,\mathbb{R}^m)$ とみた時に、「$\mathbb{R}^n$側と$\mathbb{R}^m$側の基底をうまくとると、その表現がよりすっきりするよ、一番すっきりしているものを代表として、選ぼう」という話でした。

2. 群の作用
   $GL_n(\mathbb{R})$や$O(n)$は群をなします。「同値類」を群の作用として理解しよう、という話でした。そのためにどんな変換が行列に加わるのか、それらはどんな群なのか、をまとめました。

参考文献

twitter 上で池田岳先生に多くの有用な指摘を頂きました。参考にした本で重要なものは以下です。

• 佐武一郎『線型代数学』
  

• 齋藤正彦『線形代数学』
  

• 関口英子 "線型代数と群" 『数理科学 2021/10』
  

• 新井仁之『線形代数 基礎と応用』
  

• ストラング：教養の線形代数
  

ぼくは、この本の共訳者でもあり、他にもストラング先生流の線形代数の話を Qiita に書いています。こちらからどうぞ。

（ここまで）