佐武の『線型代数学』学習メモ

これは何?

佐武一郎先生の『線型代数学』という良書があります．基礎からテンソルまで，また，群論的な内容やLie代数的な位相につながるフレーバーも散りばめられた，初学者には難し目の本だと思います．

私は「からすま数理」というグループの毎週日曜朝の輪読会でコツコツ読み進めています．内容を図や表で説明することが好きなので，自分の手書きメモを公開します．内容的に説明が少なく，メモのみで分かるのは難しいと思いますが，せっかく書き溜めているので公開します．

この本を勉強している方の何かの参考になると嬉しいです．からすま数理，線形代数チャネルの Gaku Takaragi さんと sy_eng さんに感謝します．

第II章 行列式

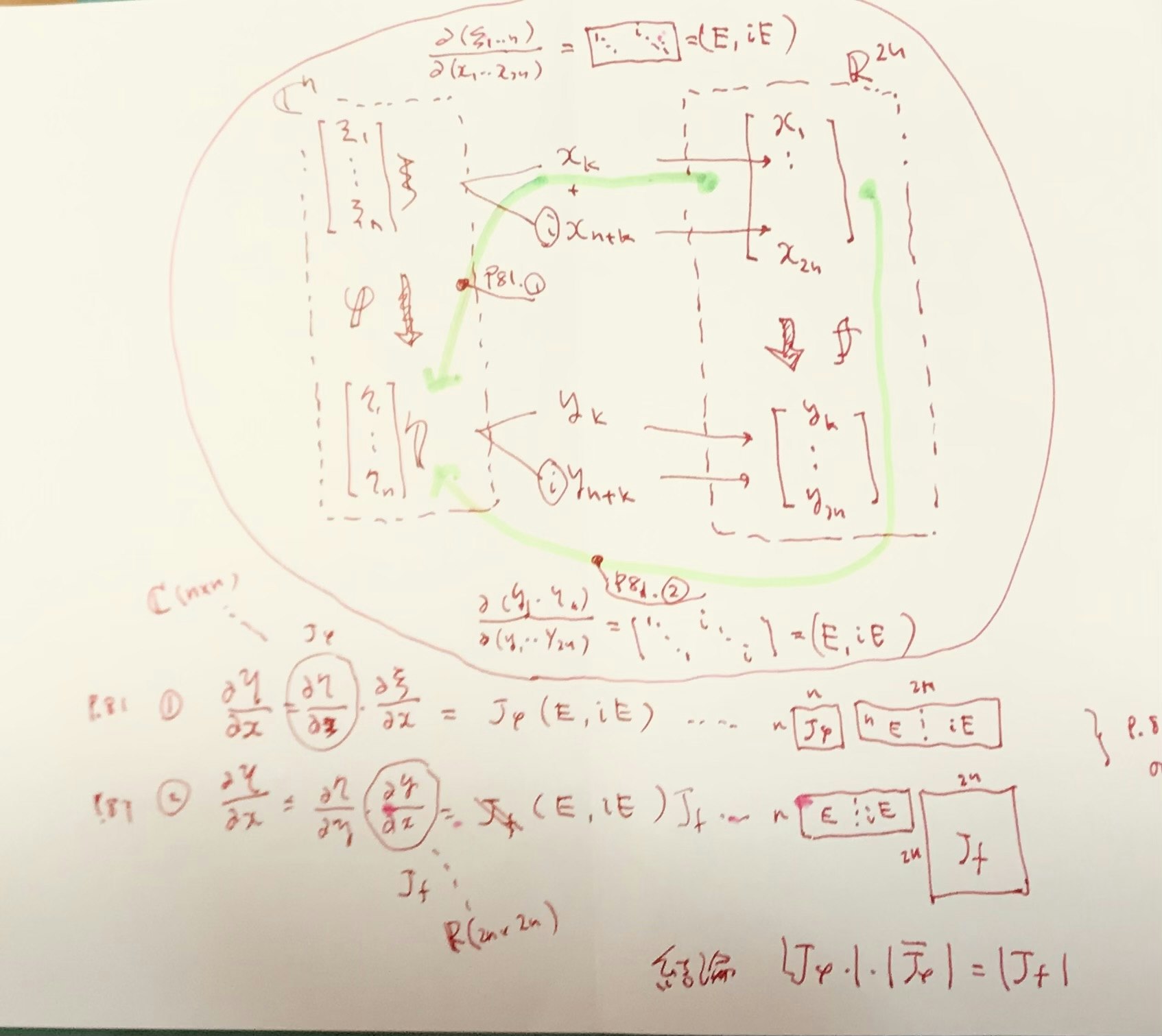
p.81-82 偏微分の Jacobian

p.82-83 巡回行列

離散フーリエ展開と同じ式が現れます．

巡回行列の線形結合として表現できます．

第III章 ベクトル空間

p.94 基底の数の一意性

別証を行列表示

p.97 系　Gram の行列式

p.112　定理9 次元定理

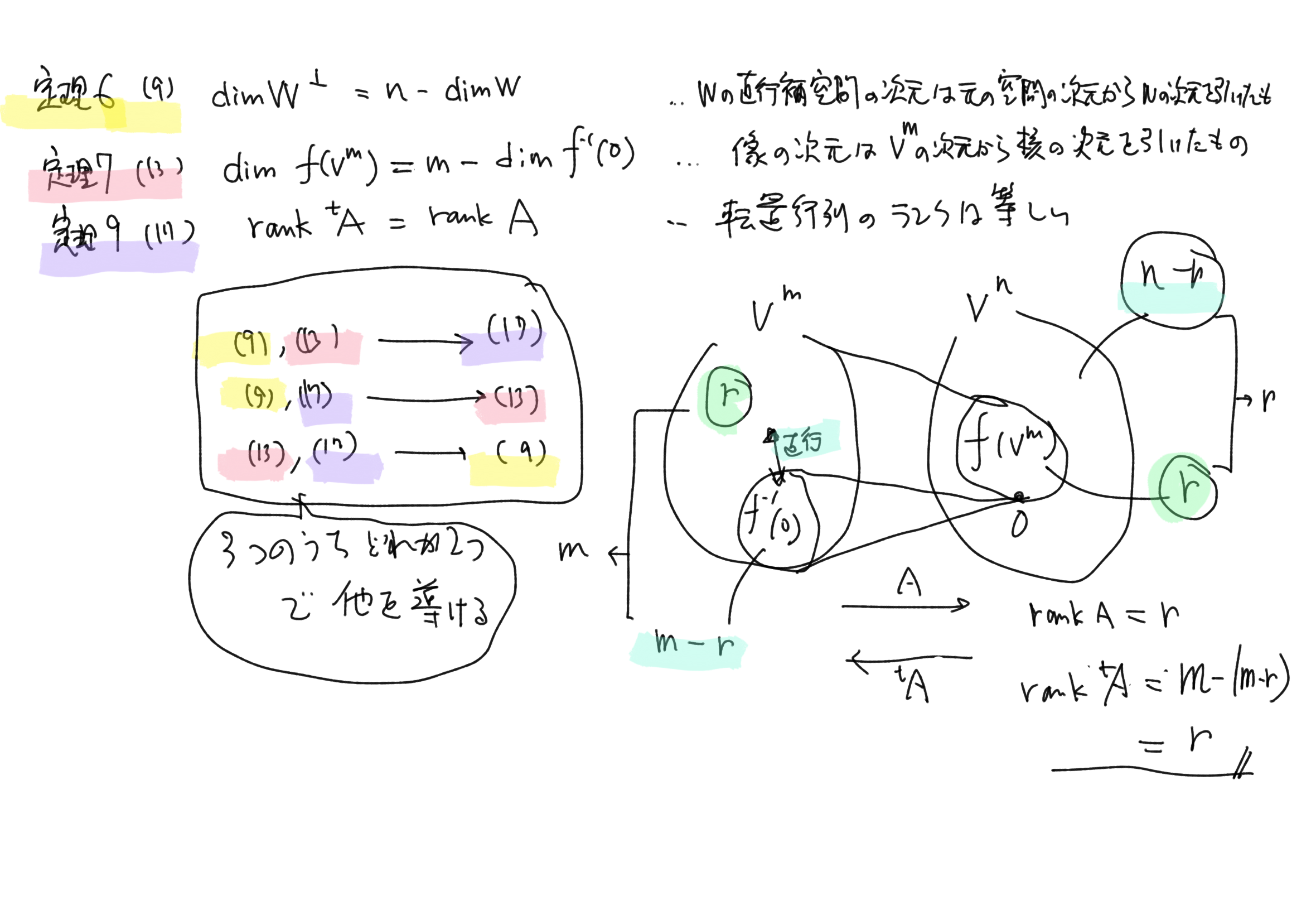
いわゆる「次元定理」とか「線型代数学の基本定理」といわれています．Strang 先生の本を元に解説した記事もあります．

第IV章　行列の標準化

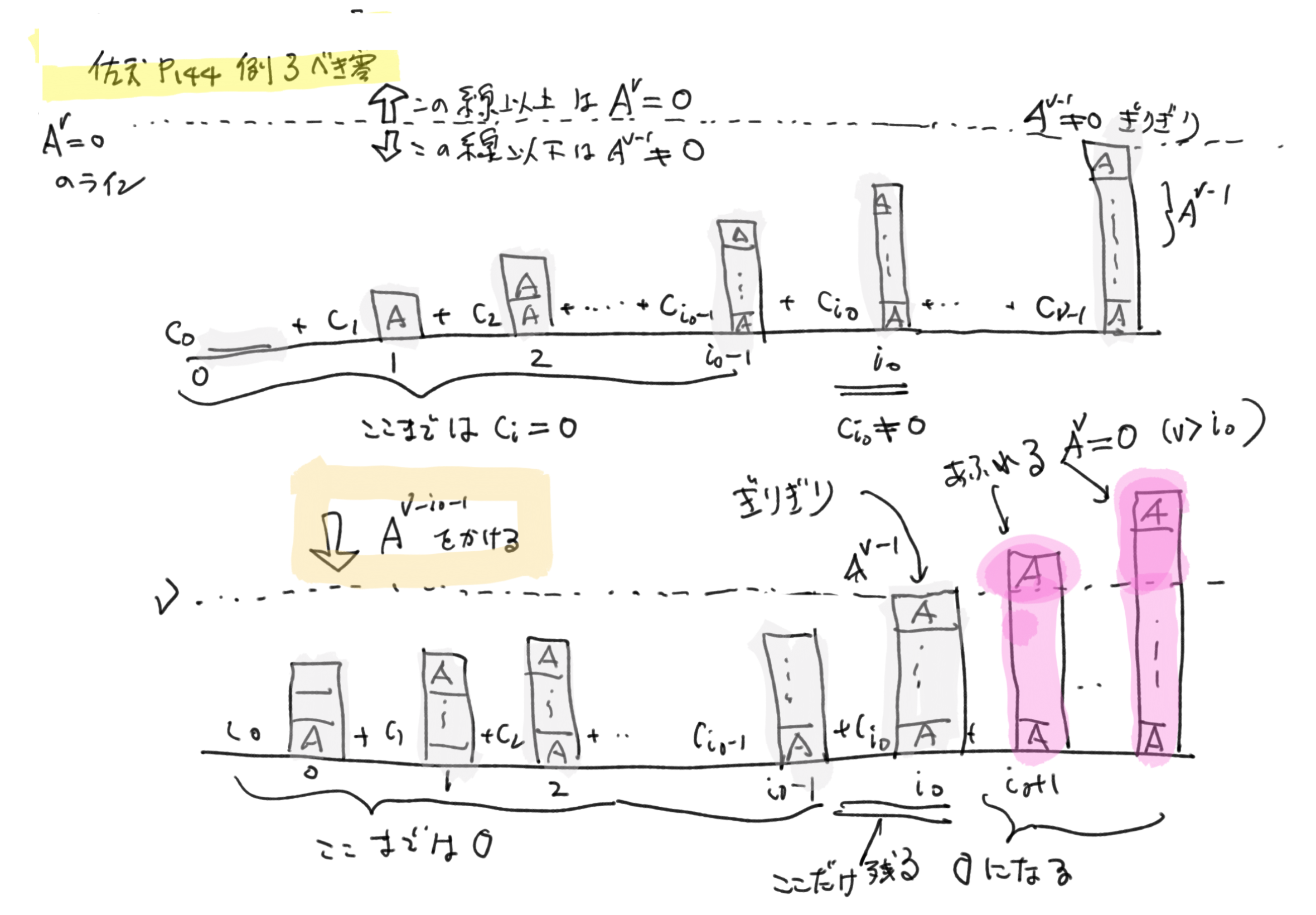
p.144 例3 冪零行列から基底を作る

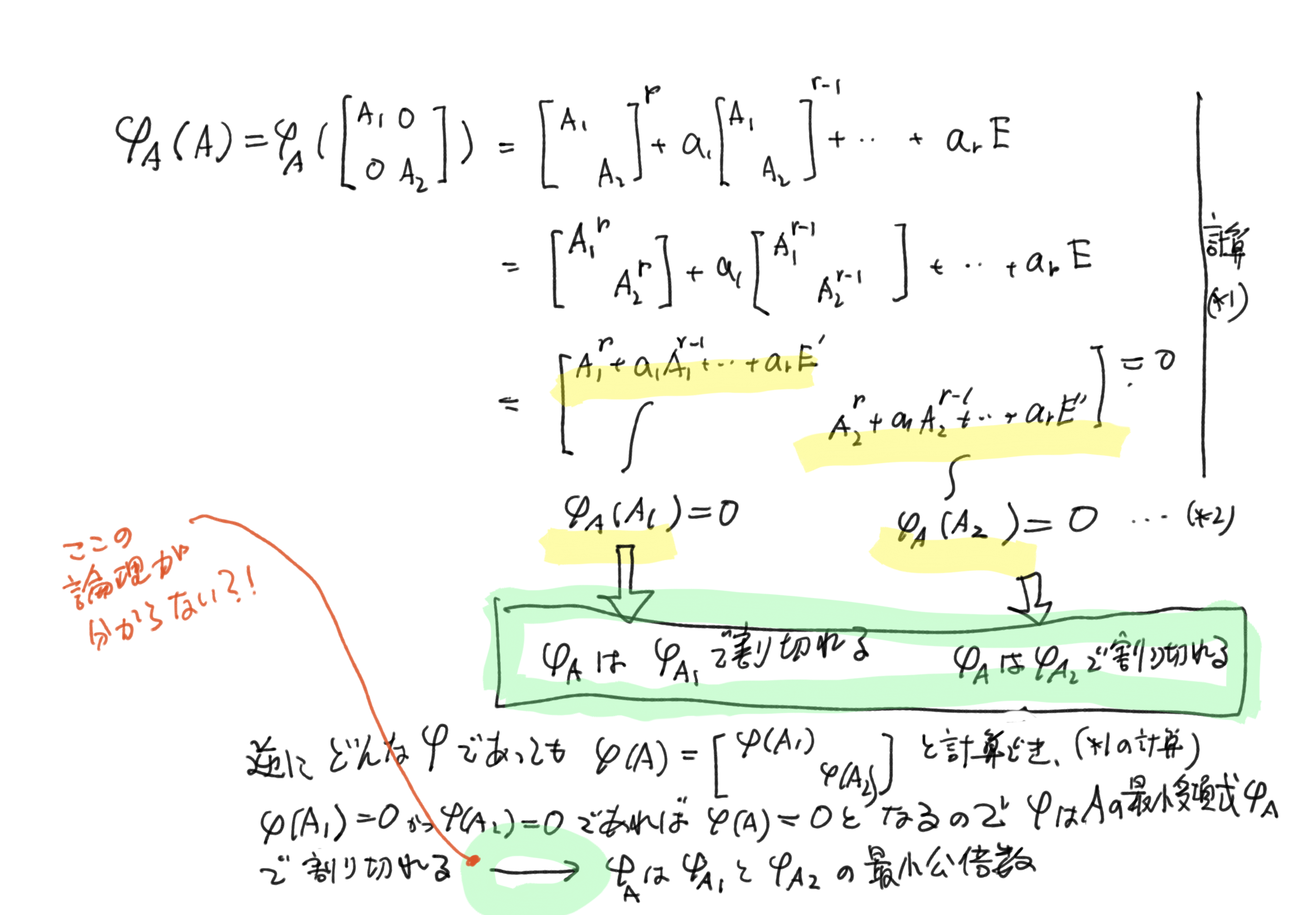
p.145 問4 最小多項式とブロック行列

$\phi_A$は$A$の最小多項式です．$A$が$A_1, A_2$に対角ブロック分解されたときに， $\phi_A$ は， $\phi_{A_1}$と$\phi_{A_2}$ の最小公倍式であることを示します．

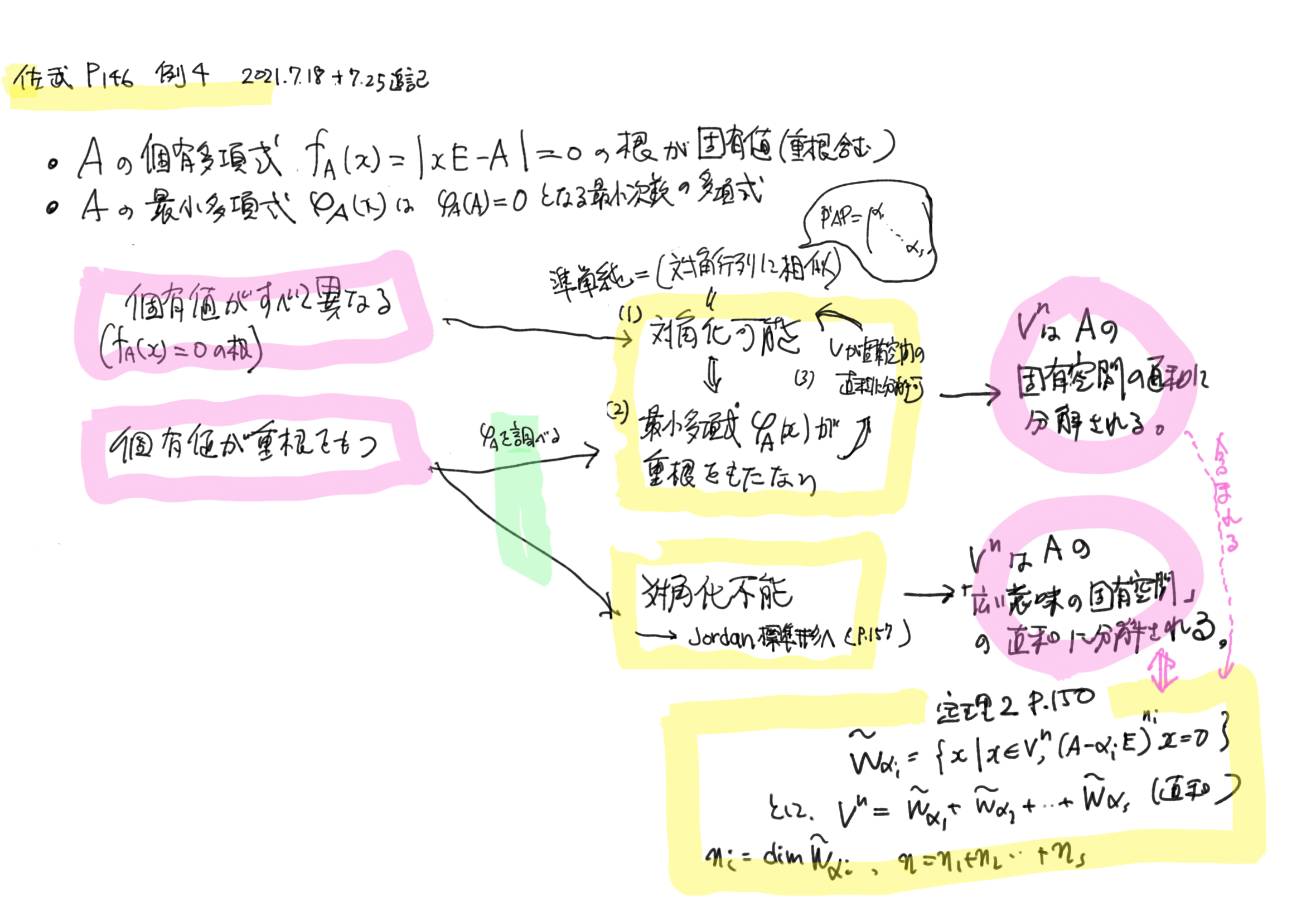
p.147-152 例4 固有多項式/最小多項式と，固有値の重解の関係

p.150 補題1-定理2 固有多項式・最小多項式，中国剰余定理

いわゆる中国剰余定理およびベズーの定理（互いに素な多項式は，線型結合を使って「1」を作ることができる）を使って，広義の固有空間（A-不変な部分空間）にVをに分割できることを，射影子の存在を持って示しています．

和に分解された多項式は，それぞれの広義固有空間への「射影子」となります（射影子と広義の固有空間は，双対関係にあります）．射影子を使って広義固有空間への分割を言うという論法です．

Steven Roman 先生は，「Resolution of Identity」と言う言葉で "単位行列を独立した射影の和に分解する（Vを充満する直和）" という性質としています．

P_1+P_2 + \ldots +P_n = I \quad \text{(resolution of identity=充満条件)}\\
P_i P_j = 0 \quad (i \ne j)  \quad \text{(直和条件)}\\
P_i^2=P_i \quad \text{(for all i)} \quad \text{(射影：上記2つから従う)}

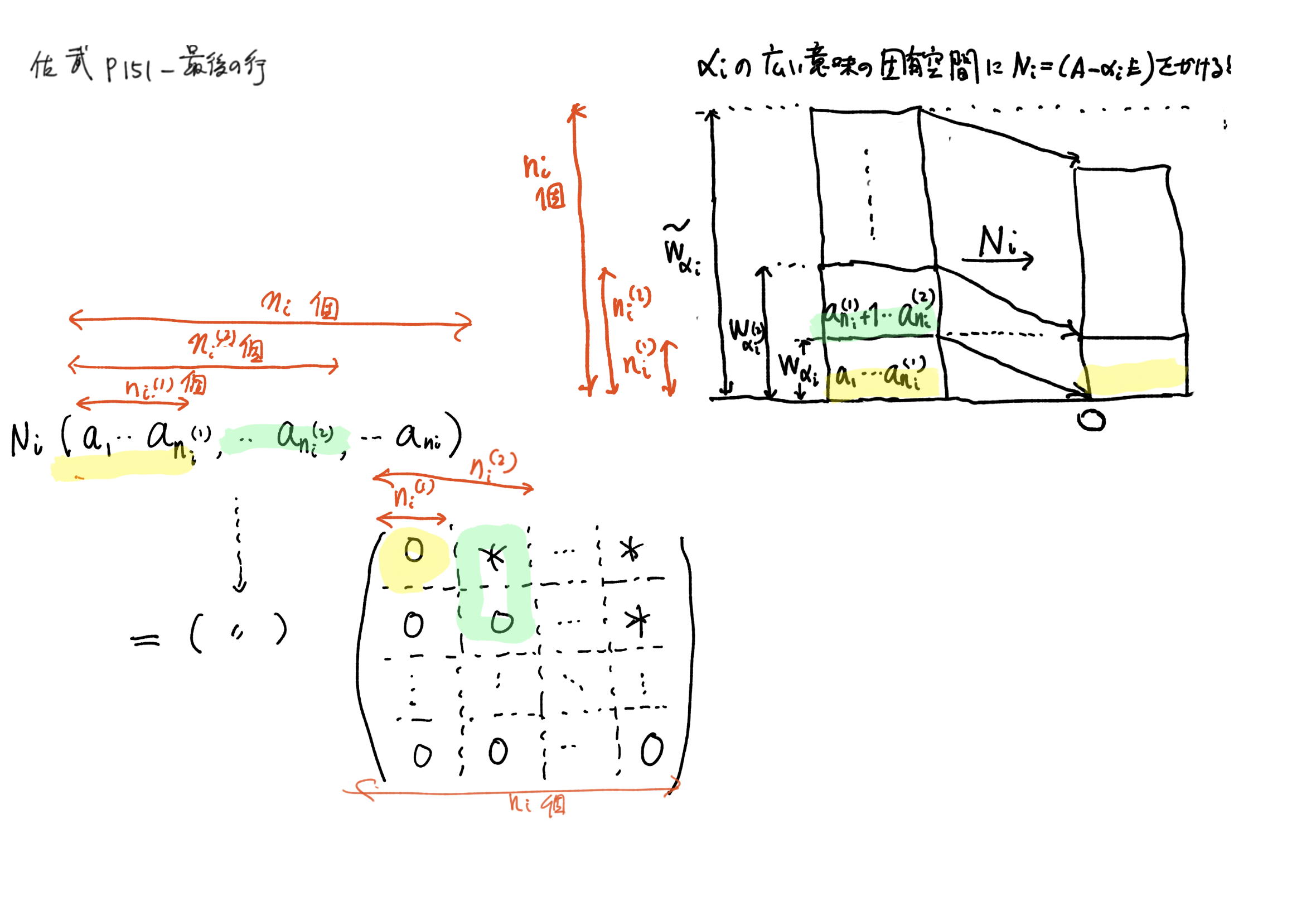
p.151 冪零行列のブロック三角化（広義固有空間の不変ブロック）

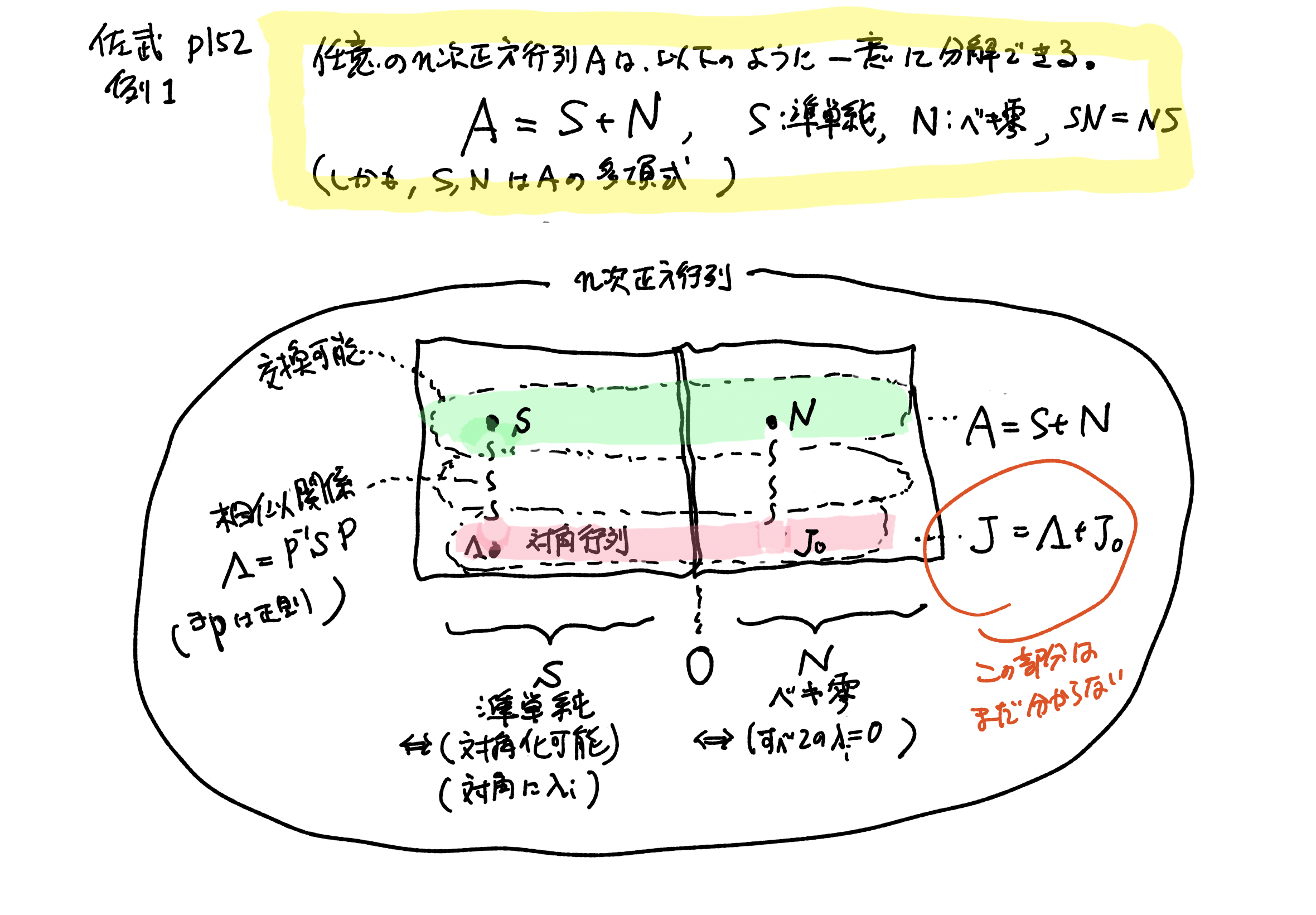
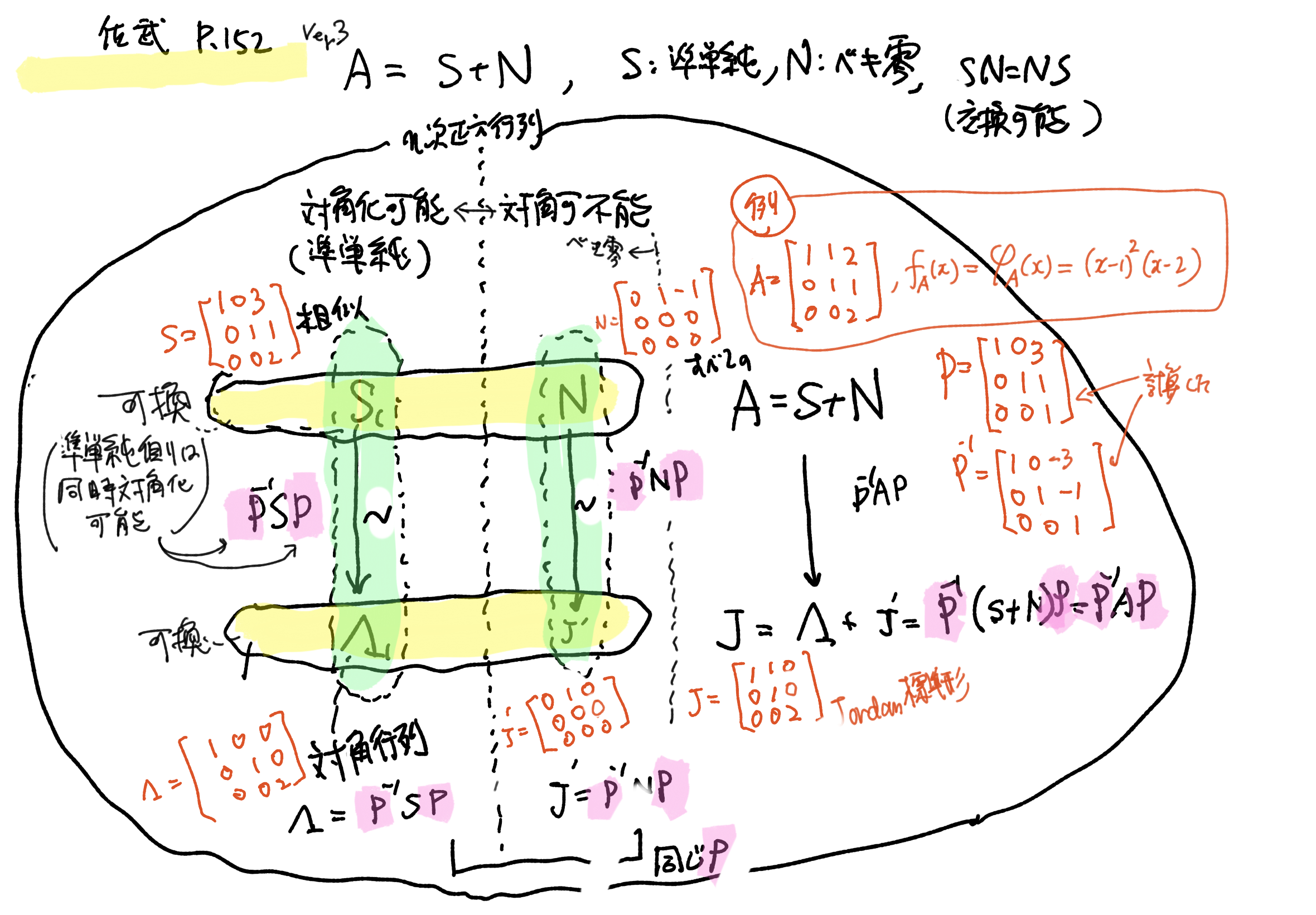
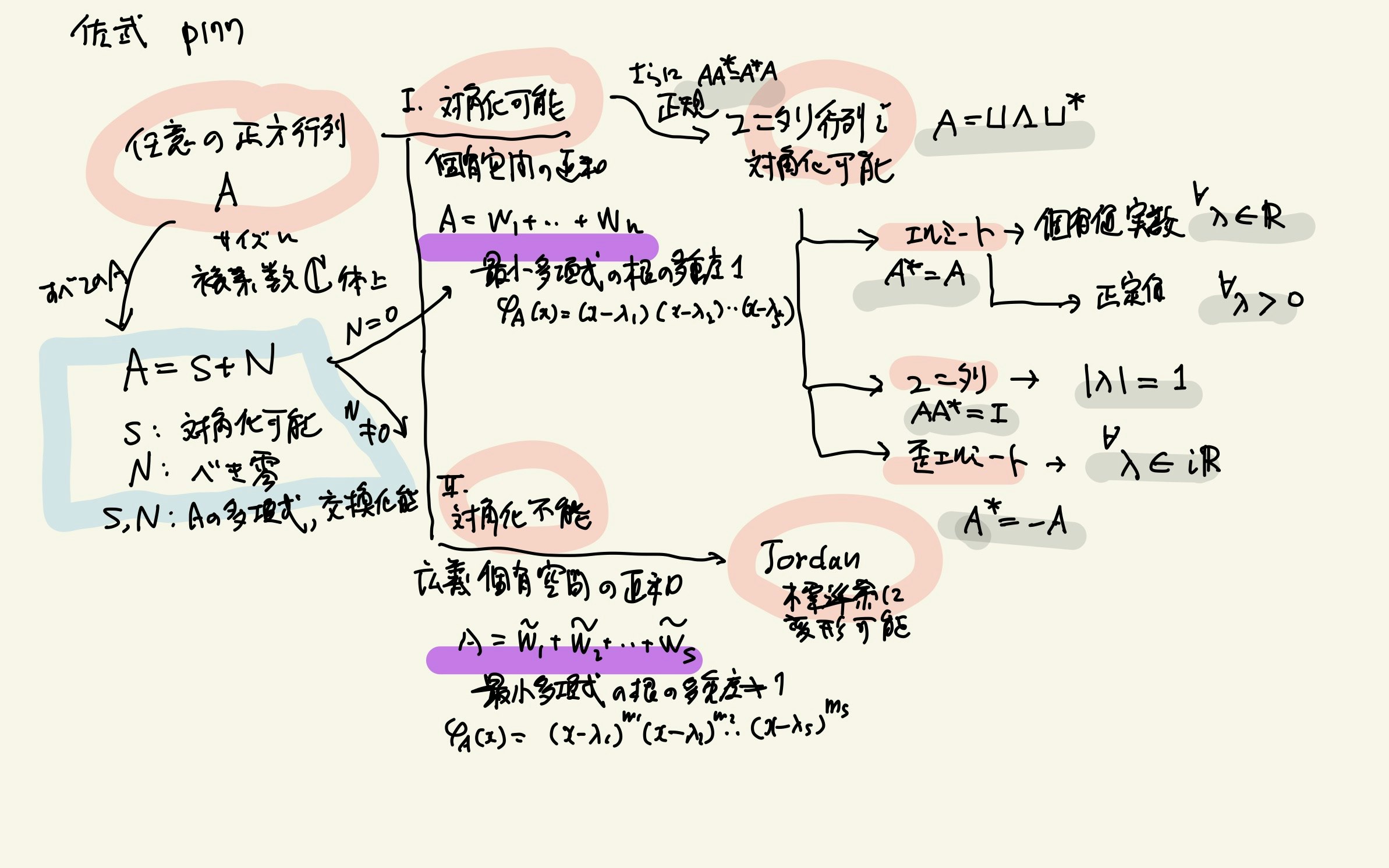
p.152 例1 任意のn次正方行列Aは，可換な準単純Sと冪零Nの和 - A=S+N

ここでは，「相似関係による同値類」と「交換可能性による同値類」の2軸で行列を分類できることを示している．
さらに， $A=S+N$ という分解が一意にできる（S: 準単純=対角化可能， N: 冪零)

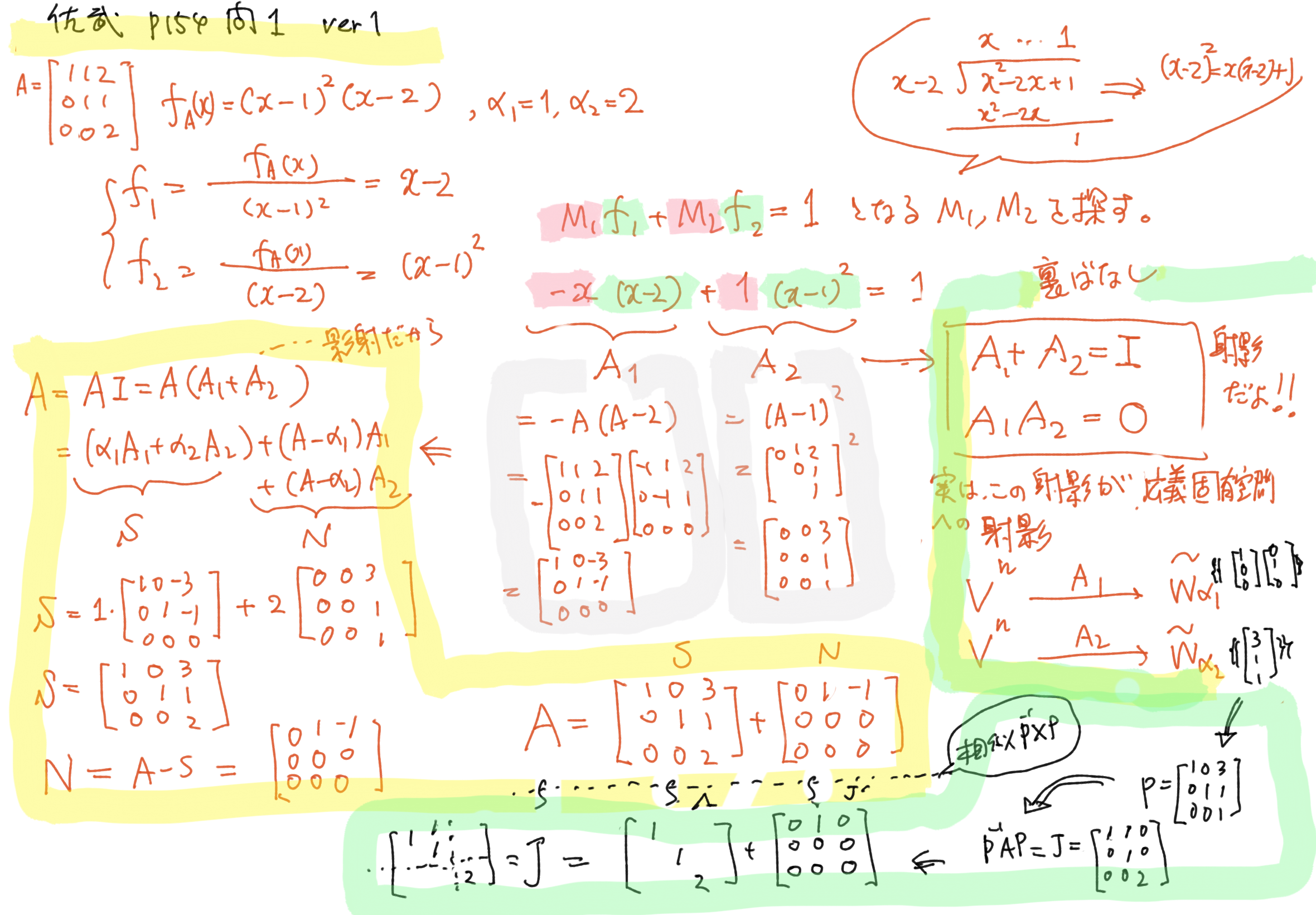
p.154 問1 射影と広義固有空間

実際の行列 $A$ を例にして，固有方程式から広義固有空間への射影行列を求めています．また，その射影行列を使って $A=S+N$ と和の Jordan 分解をしています．

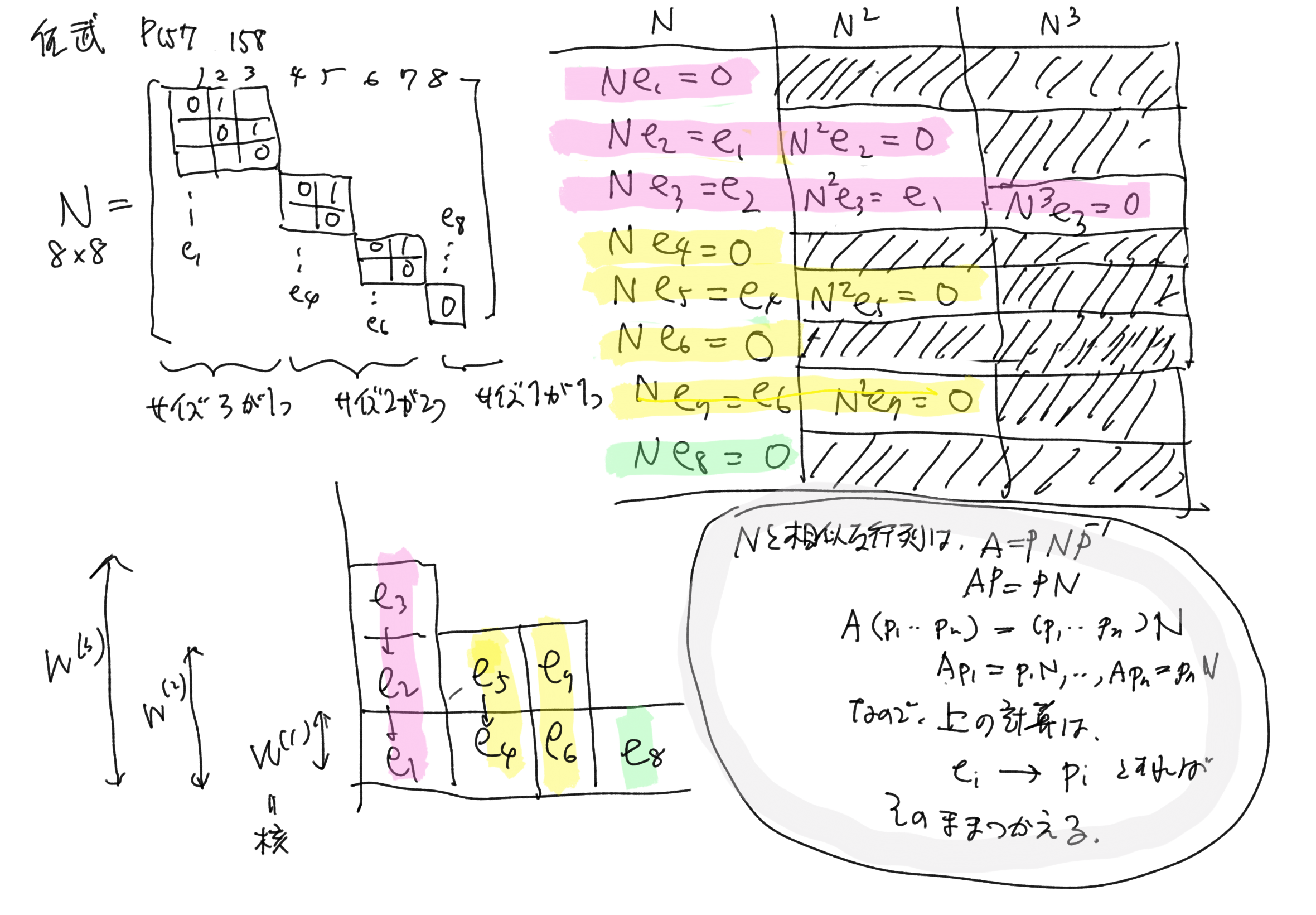
p.157,8 Jordan 分解の実例

上の行列 $A$ を例にして，冪零行列 $N=A-S$ の構造を見ています．

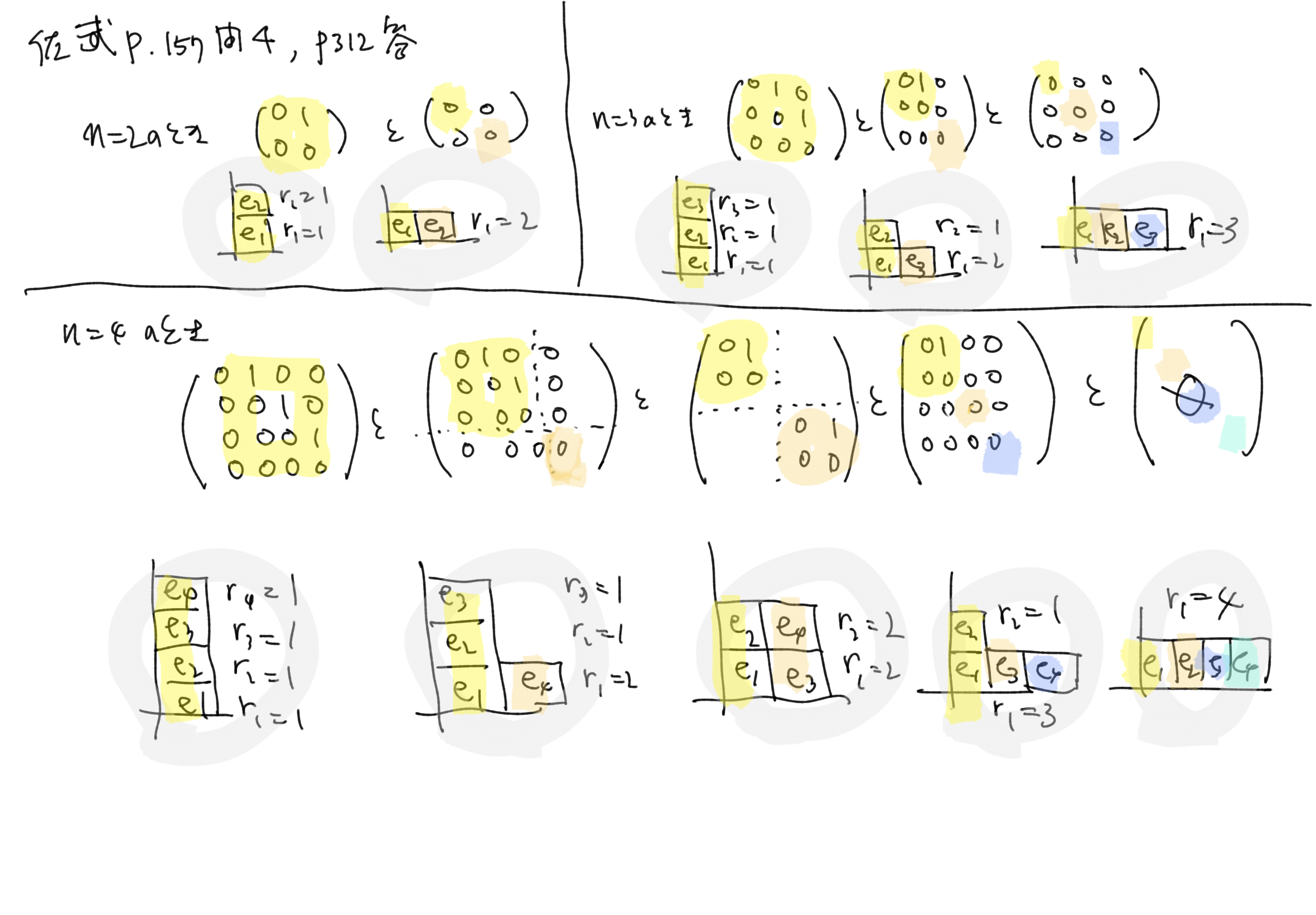
p.157 問4

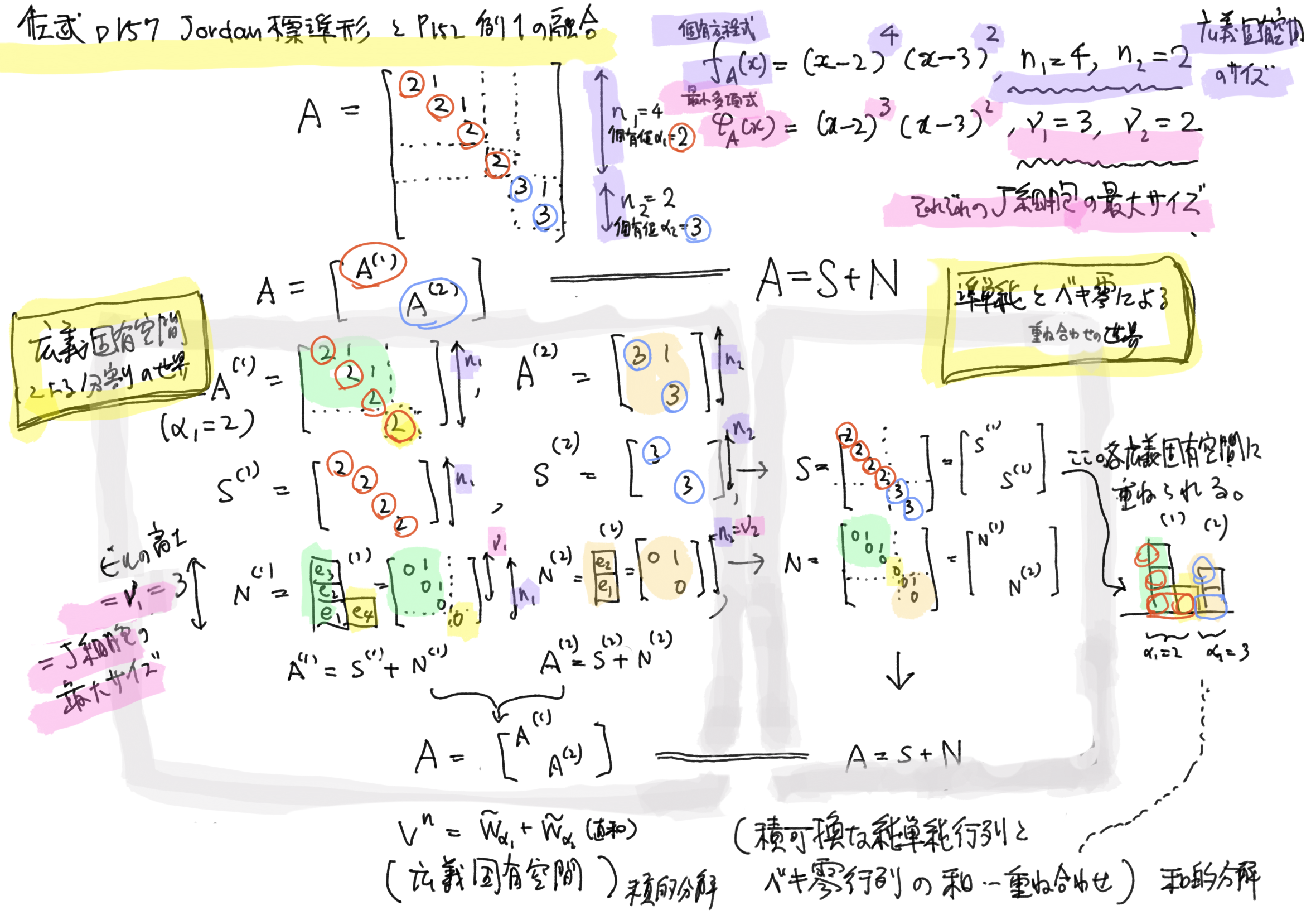
p.157 Jordan 標準形（和の表示と積の表示)

additive（和形式） と multiplicative（積形式） の両方で Jordan 標準形を表現．
どちらも， A を S(準単純=対角化可能)部分と N(冪零）部分に分解．SもNもAの多項式で表現でき，積可換である．
冪零部分(N) が分解の形を決める．

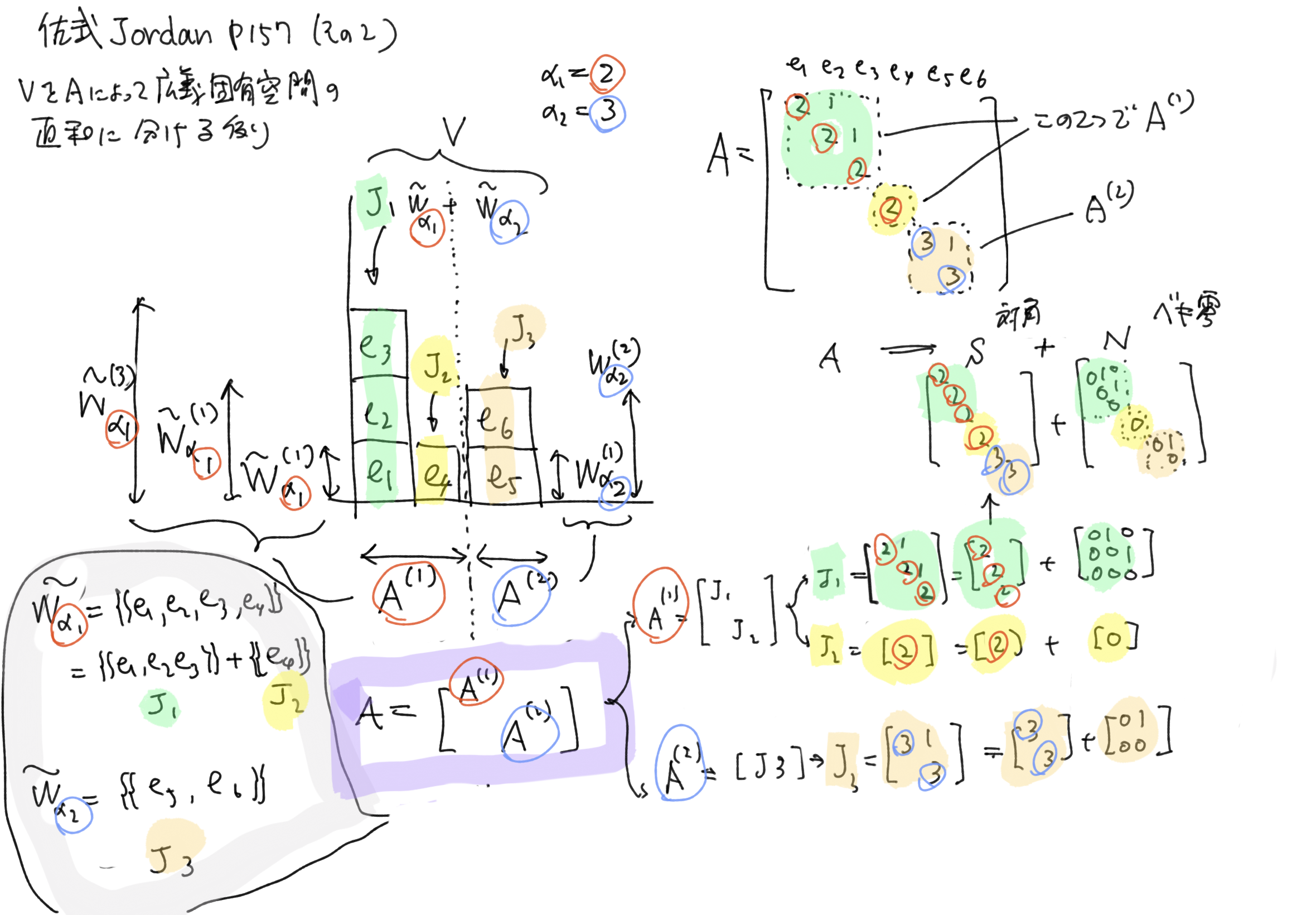
p.157 Jordan 標準形(広義の固有空間の分解イメージと例)

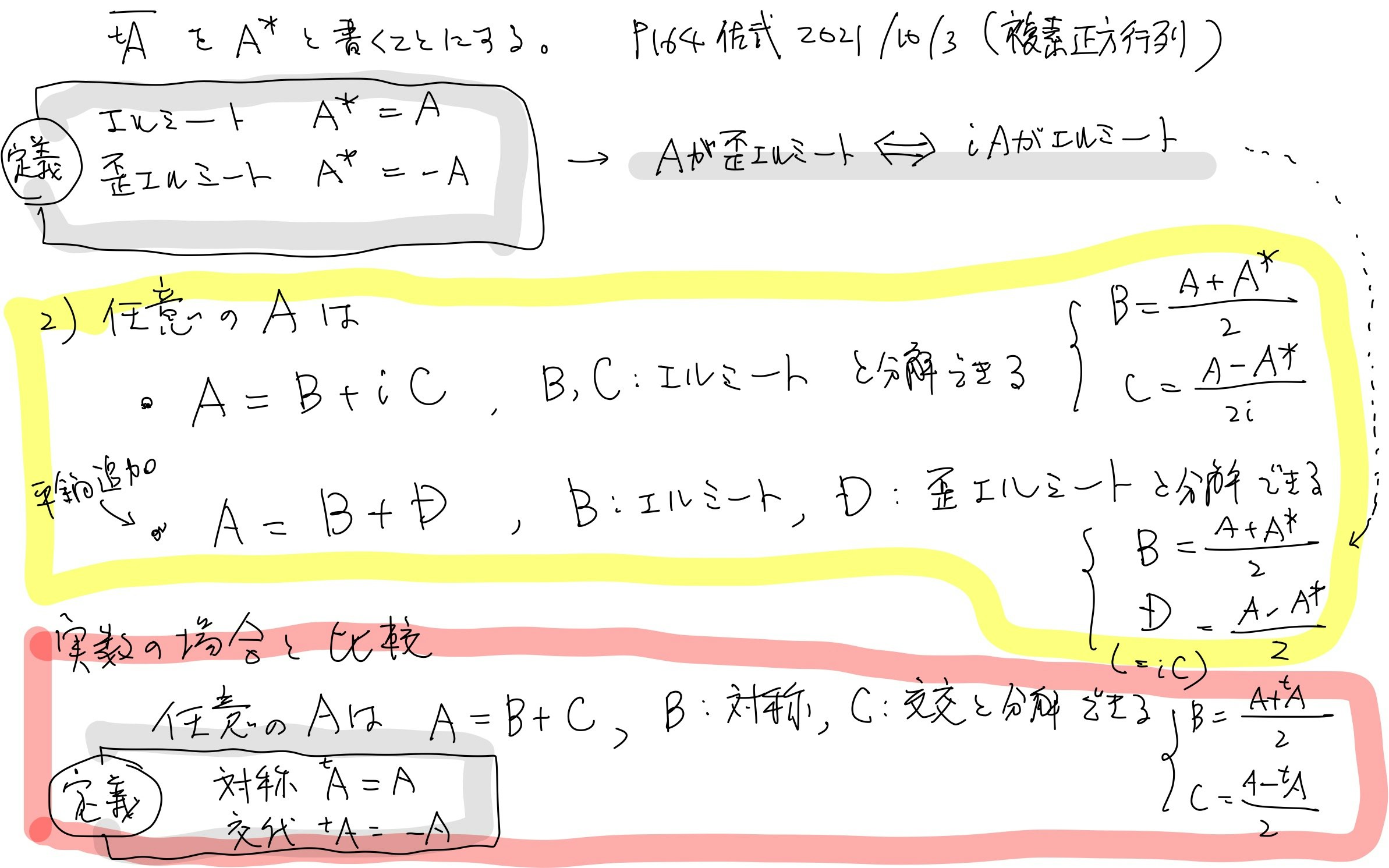
p.164 エルミートと歪エルミート

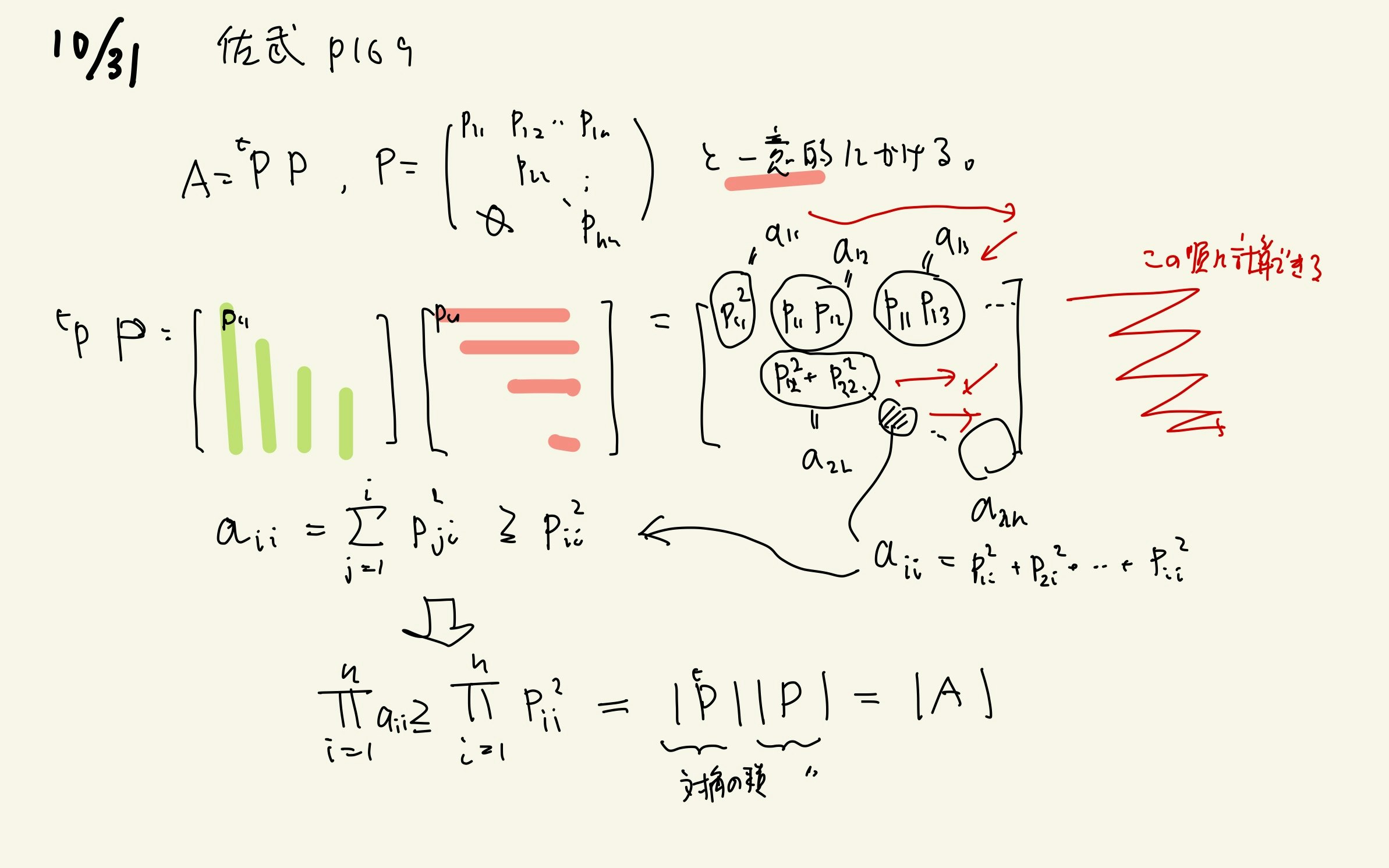
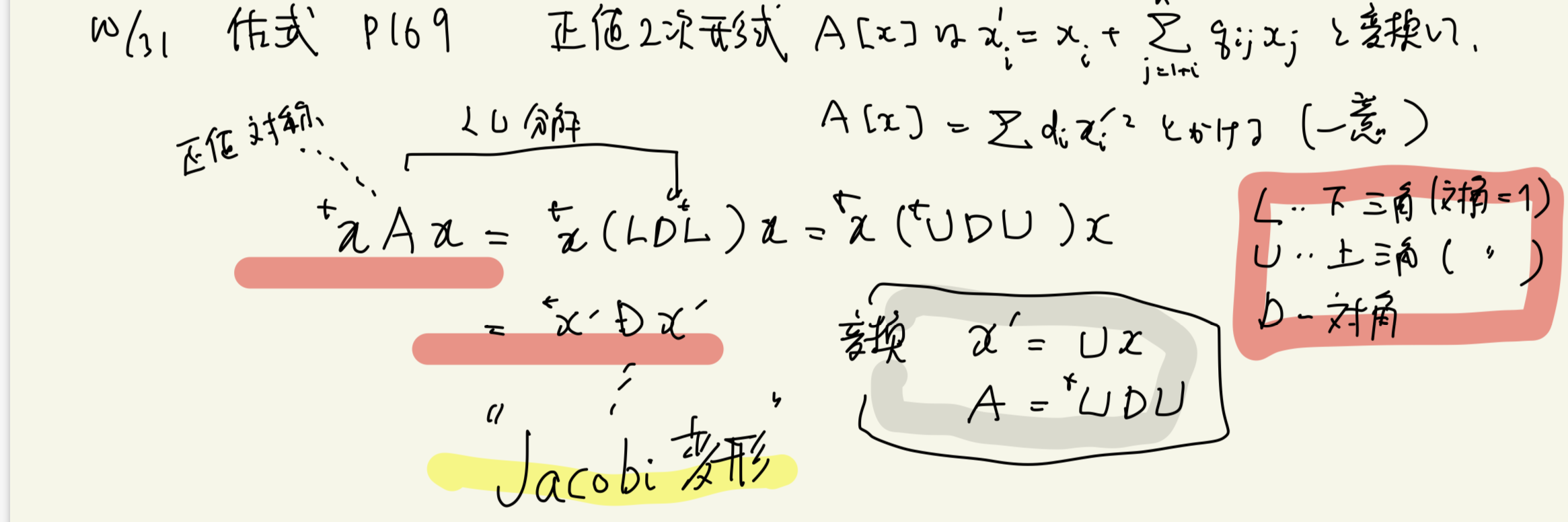
p.169 正値対称行列の転置による積分解と2次形式(Sylvesterの慣性法則)

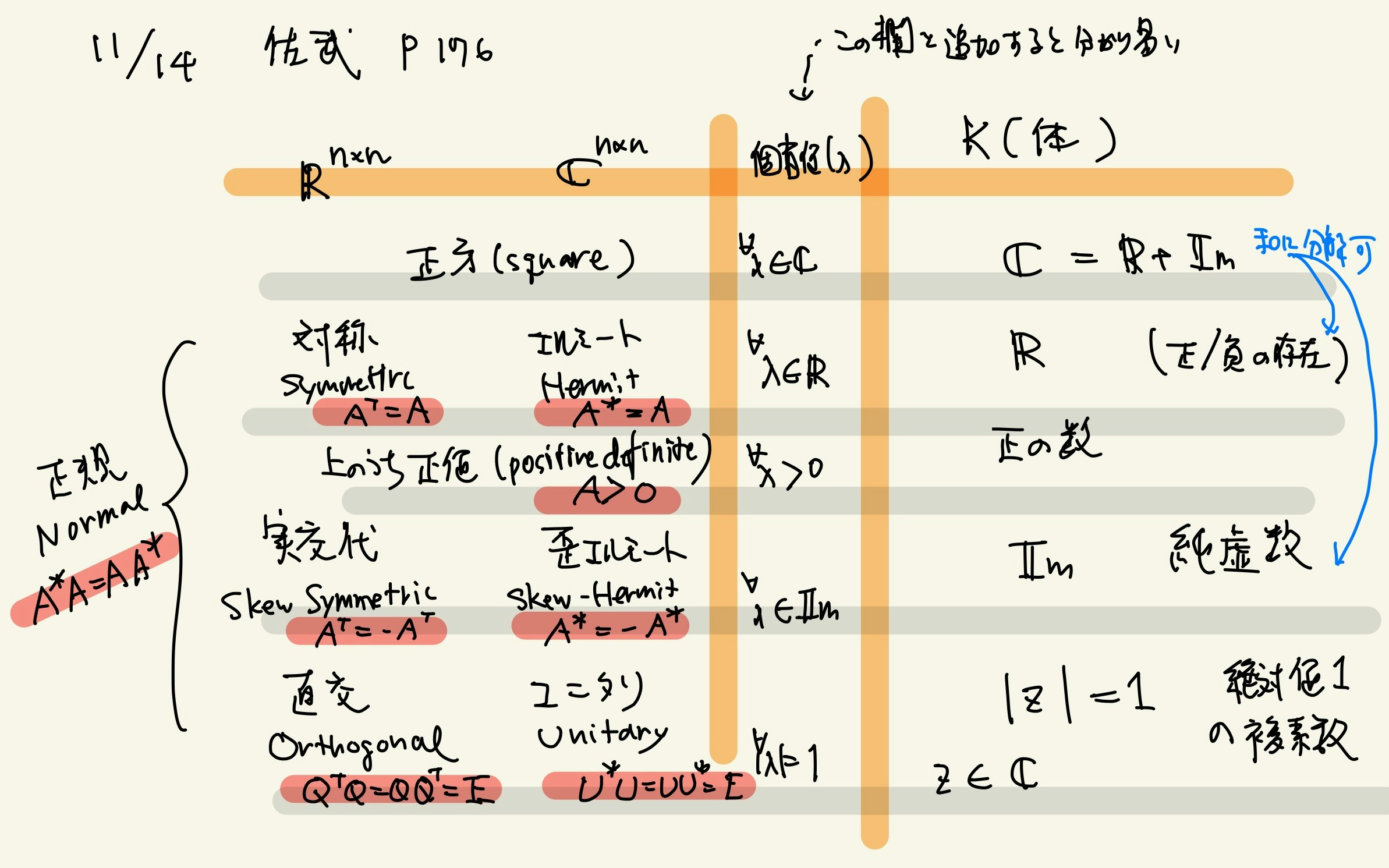
p.176 数(実数/虚数/複素数)と正則行列（特に正規行列）の類似対応

p.177 正方行列の分類と固有値

p.180 問10 実数行列の固有値の個数（Sylvester標準形）

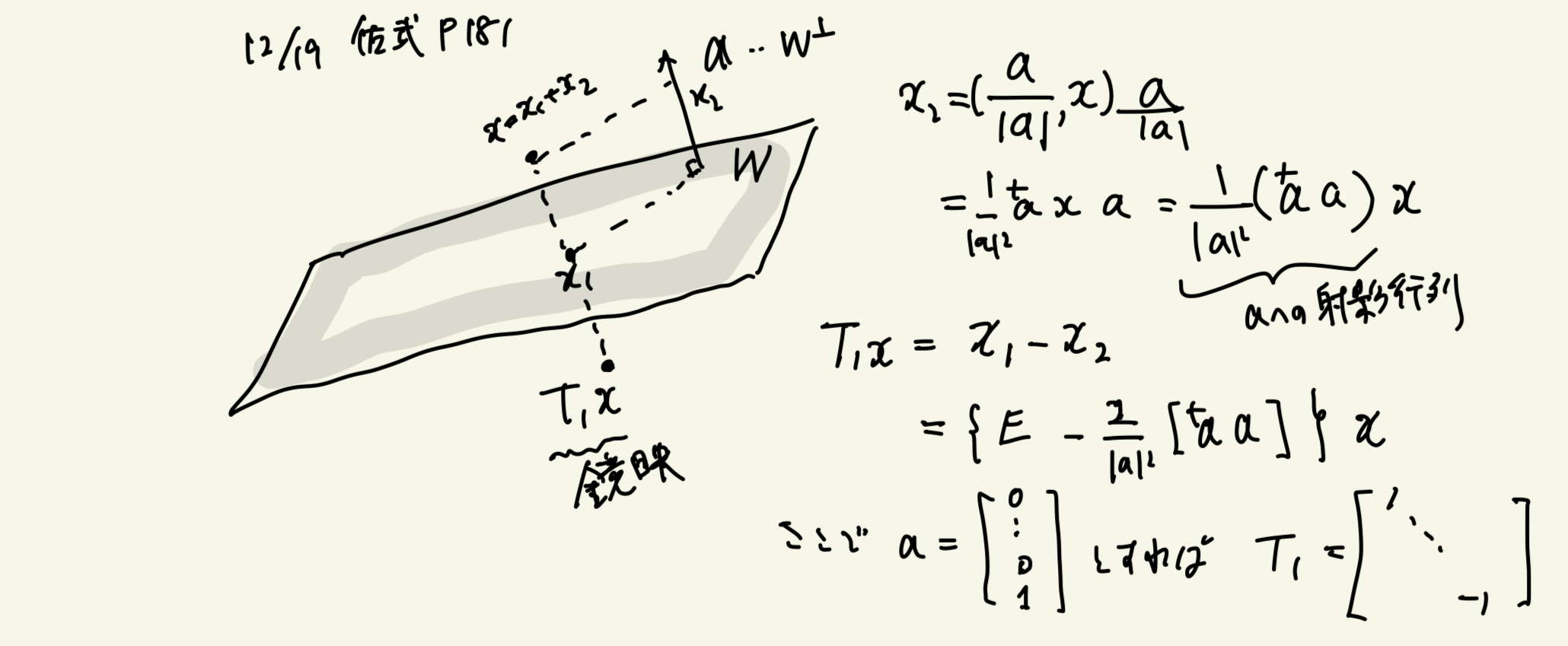
p.181 鏡映写像

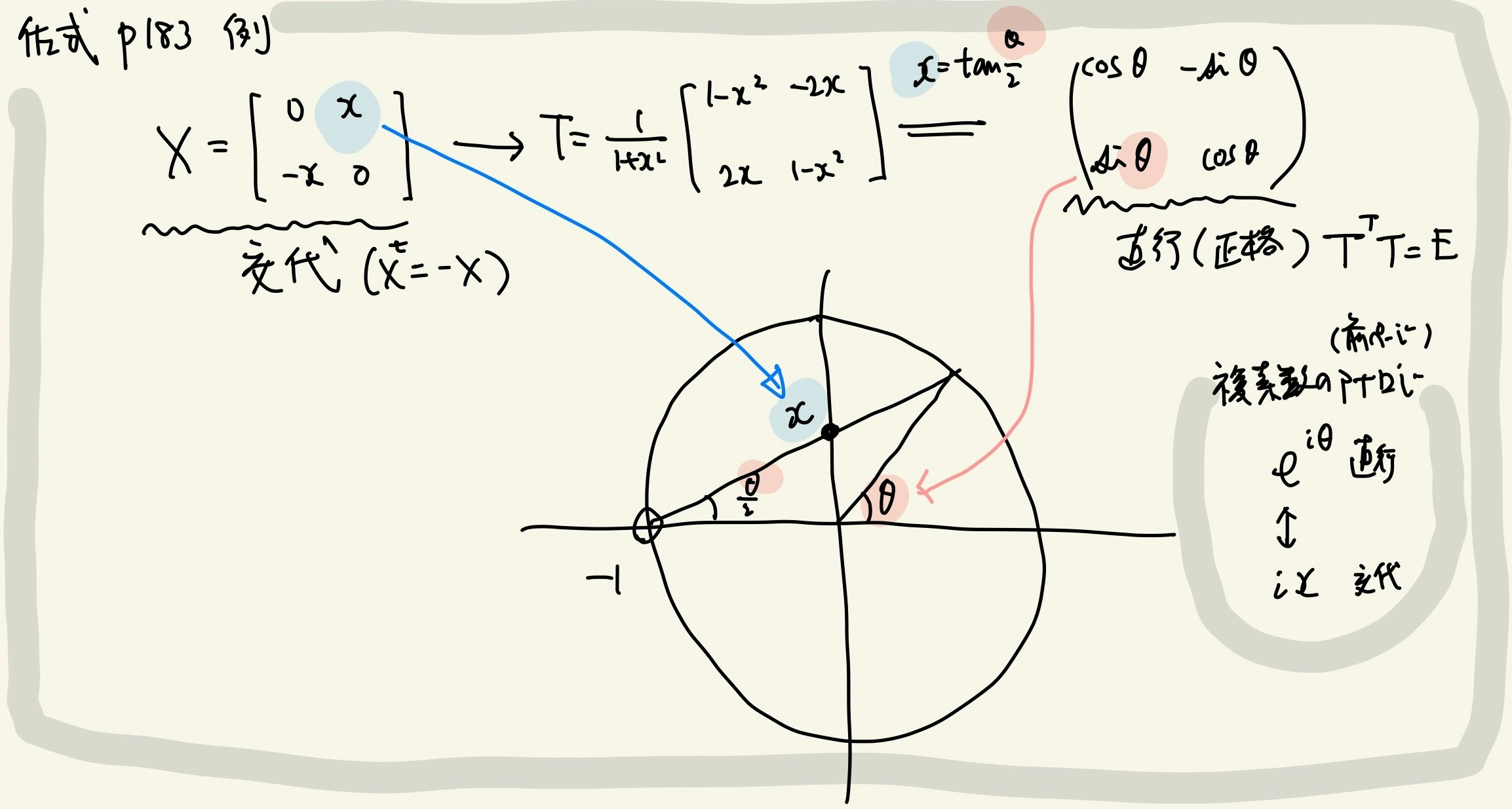
p.183 例 Cayley 変換

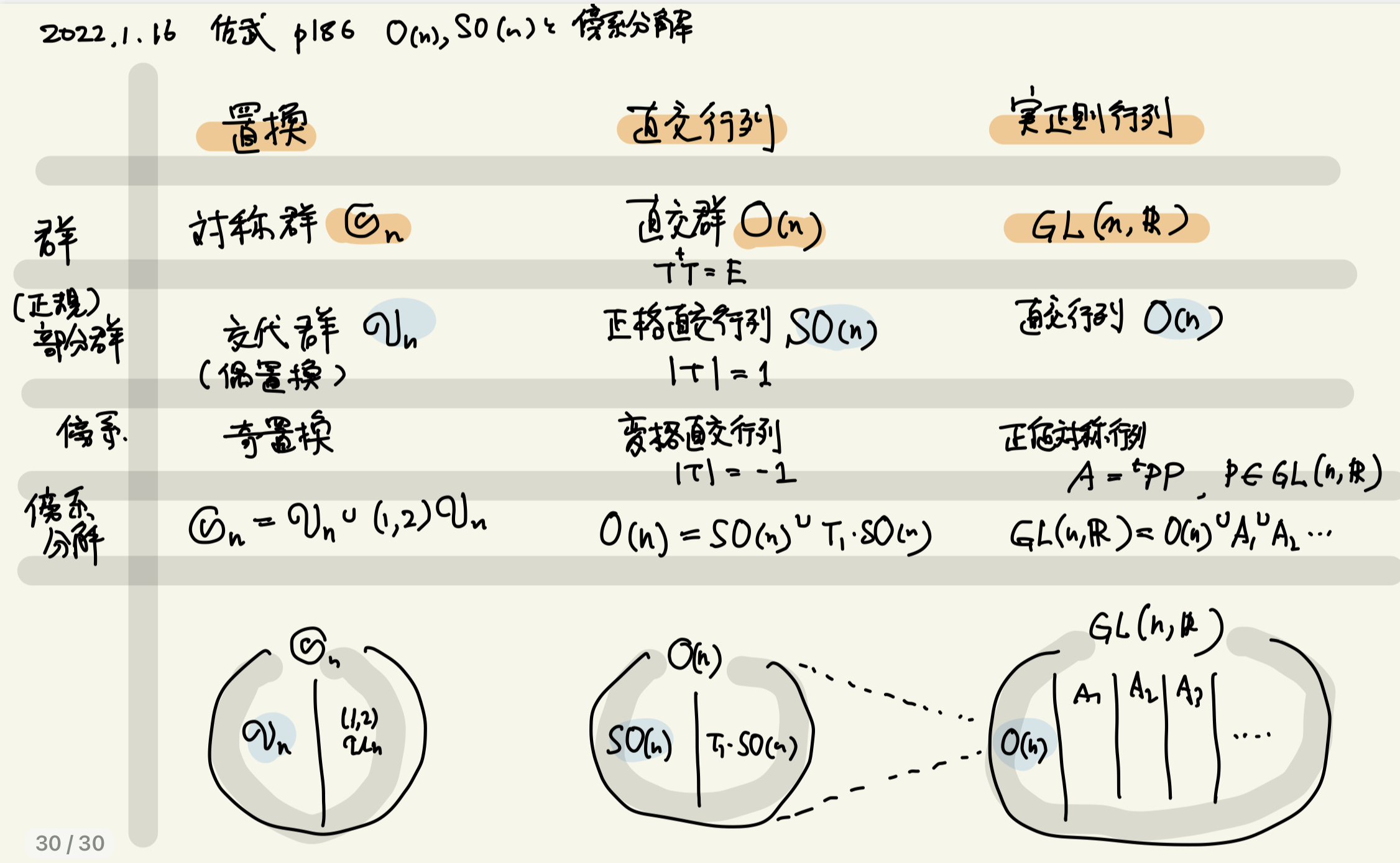
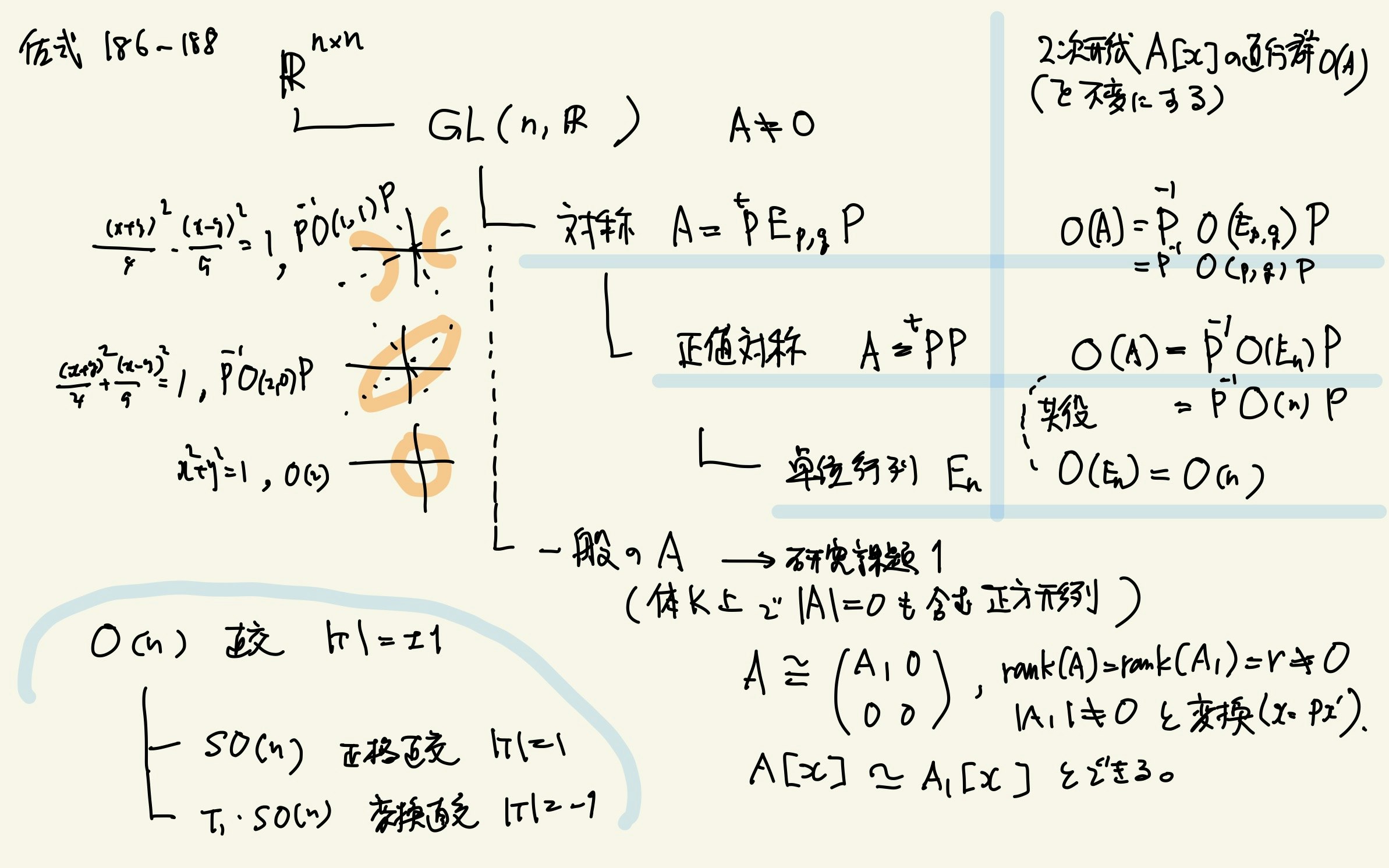
p.186 O(n)/SO(n)，GL(n,R)/O(n) の傍系分解と対称群

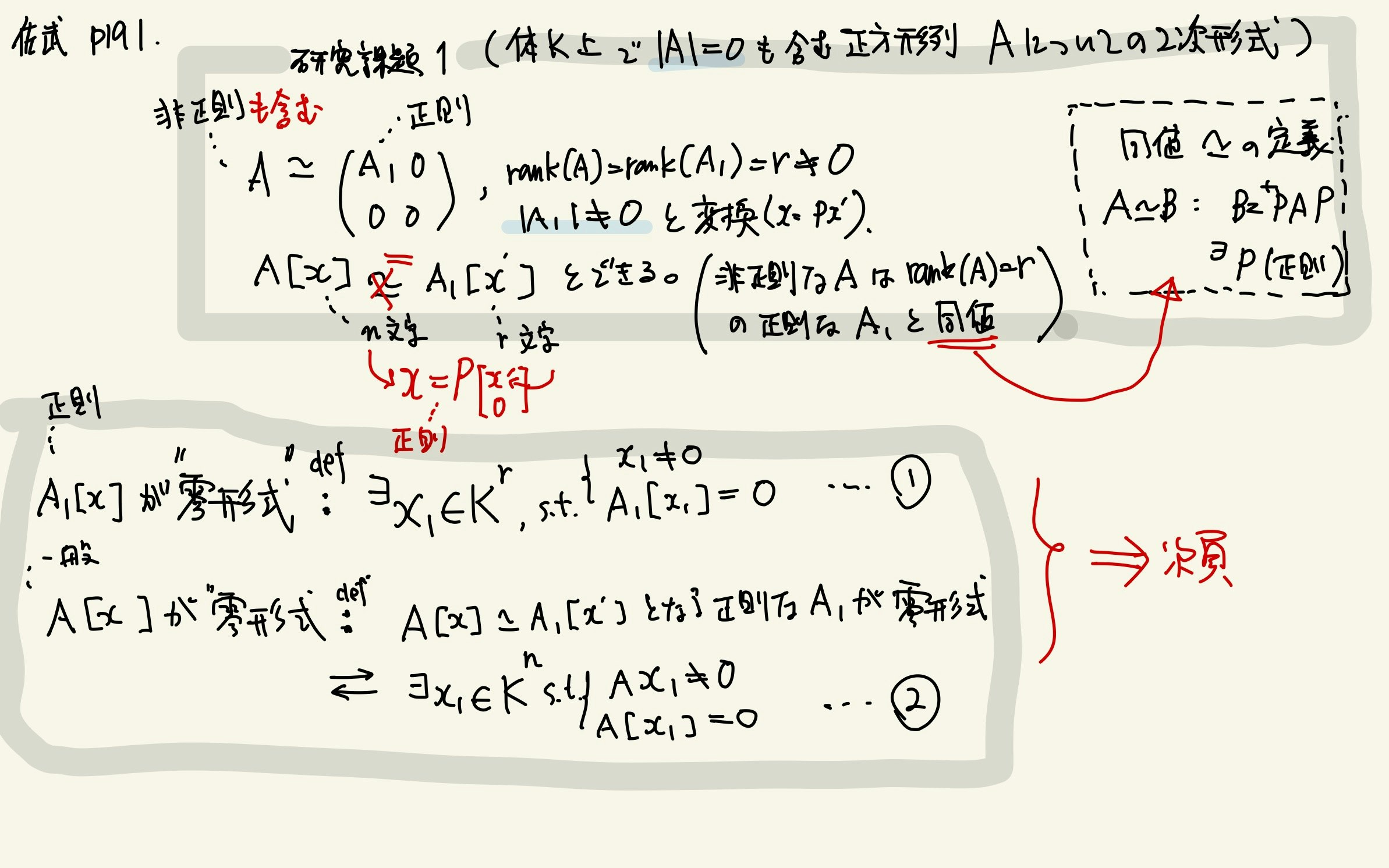
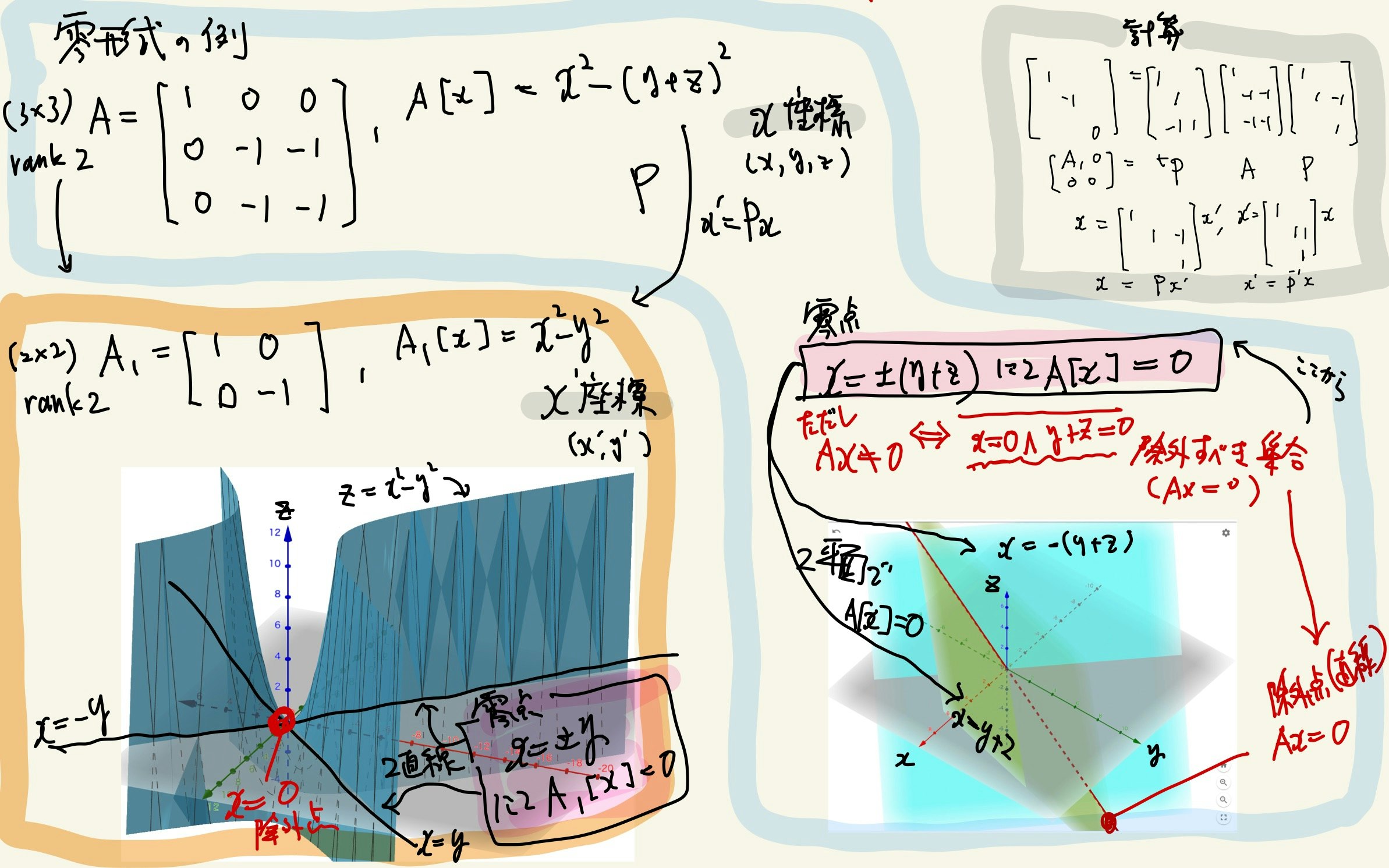
p.191 研究課題1(実数体以外の2次形式)

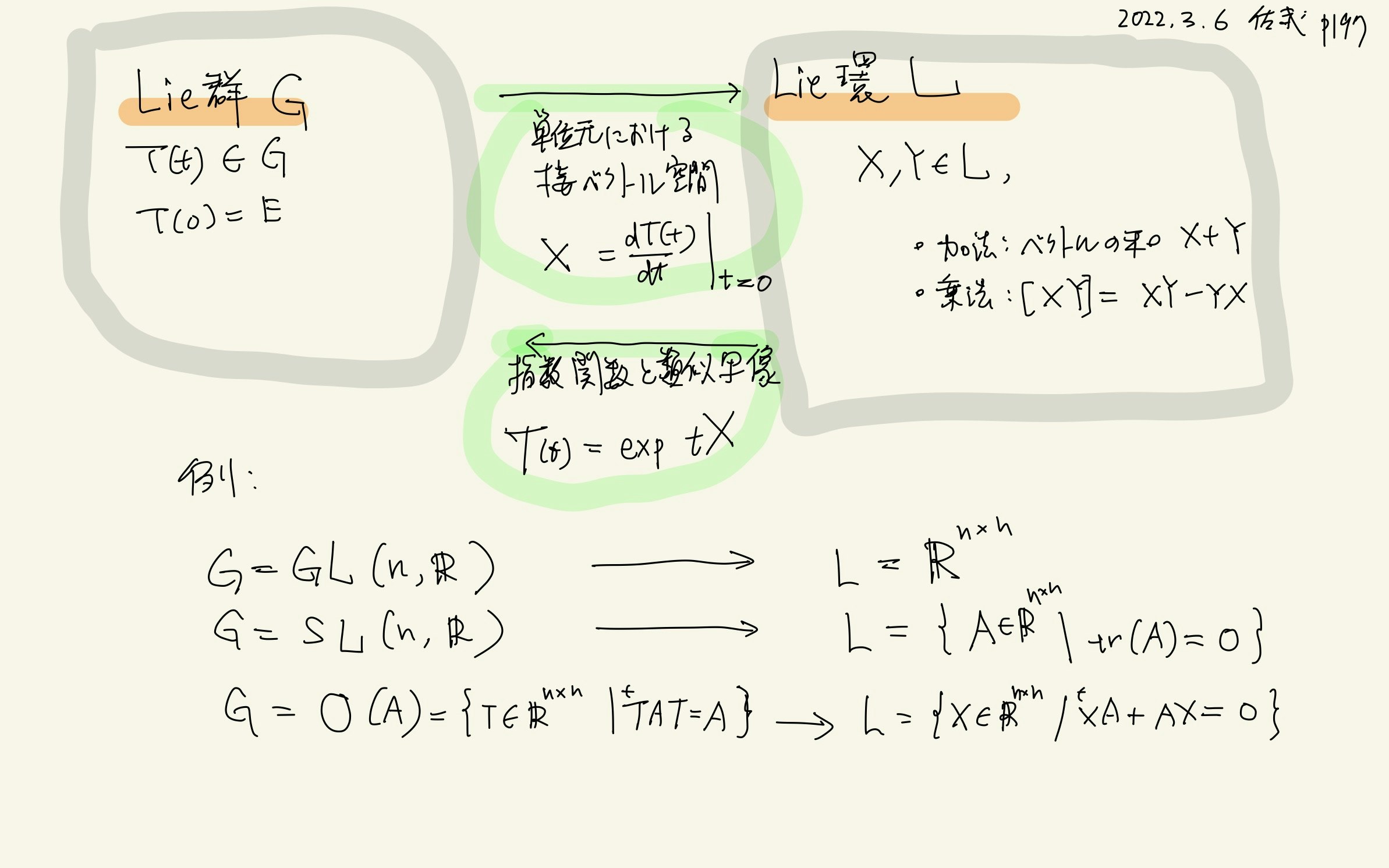
p.197 直交群のLie環

第V章 テンソル代数

p.202 双対空間

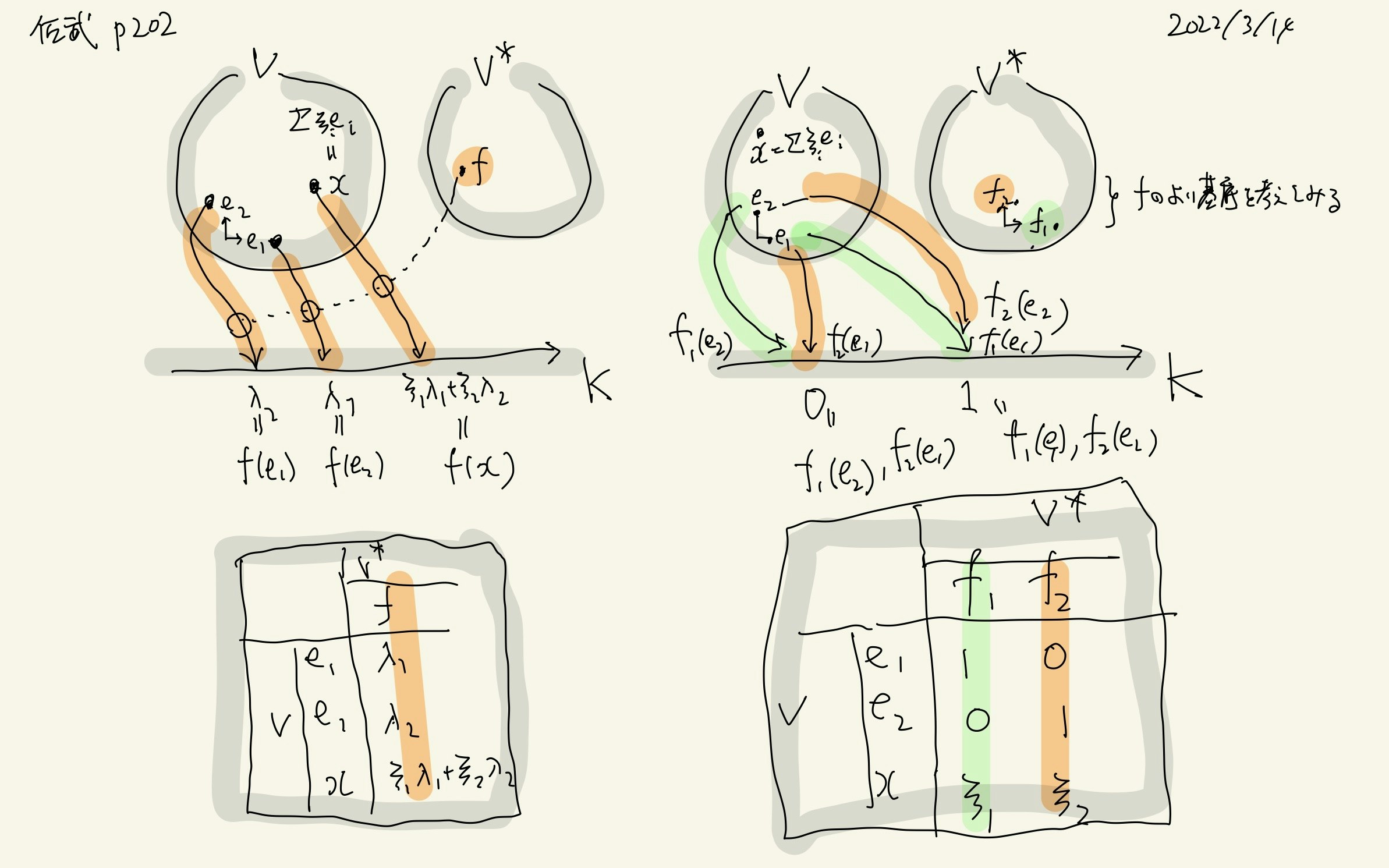
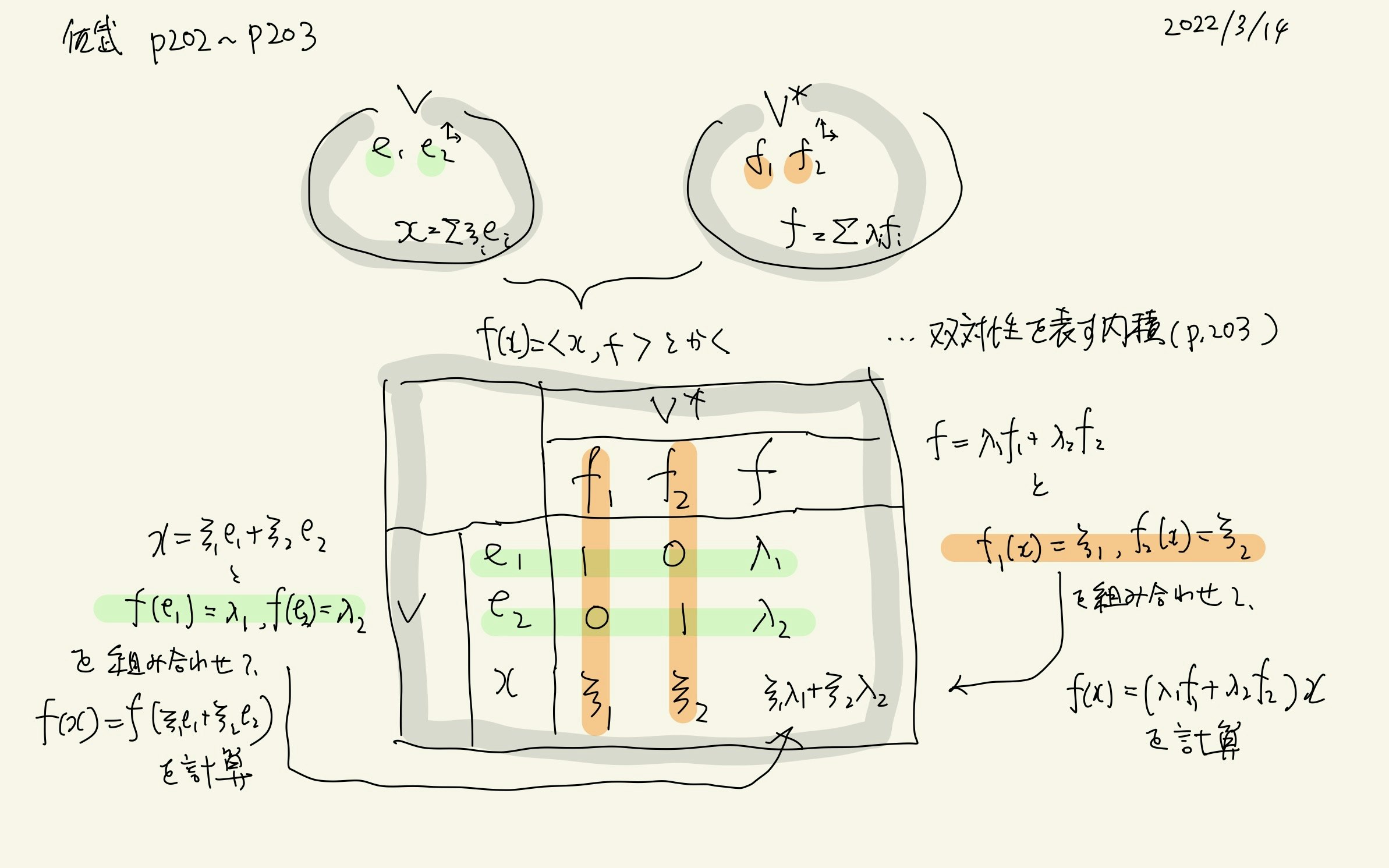
p.202-203 双対空間と双対性を表す内積

p.202 双対空間，例示

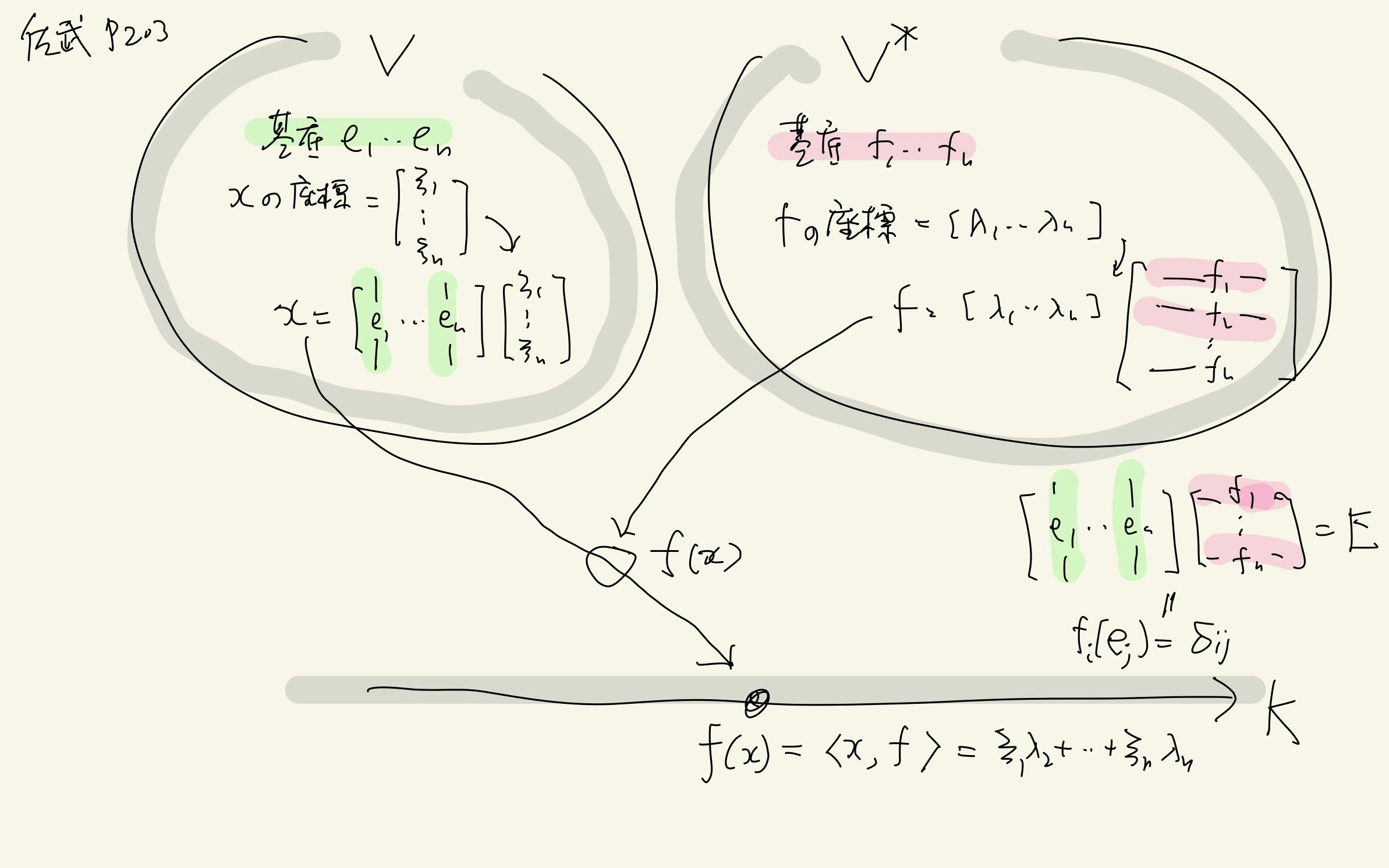
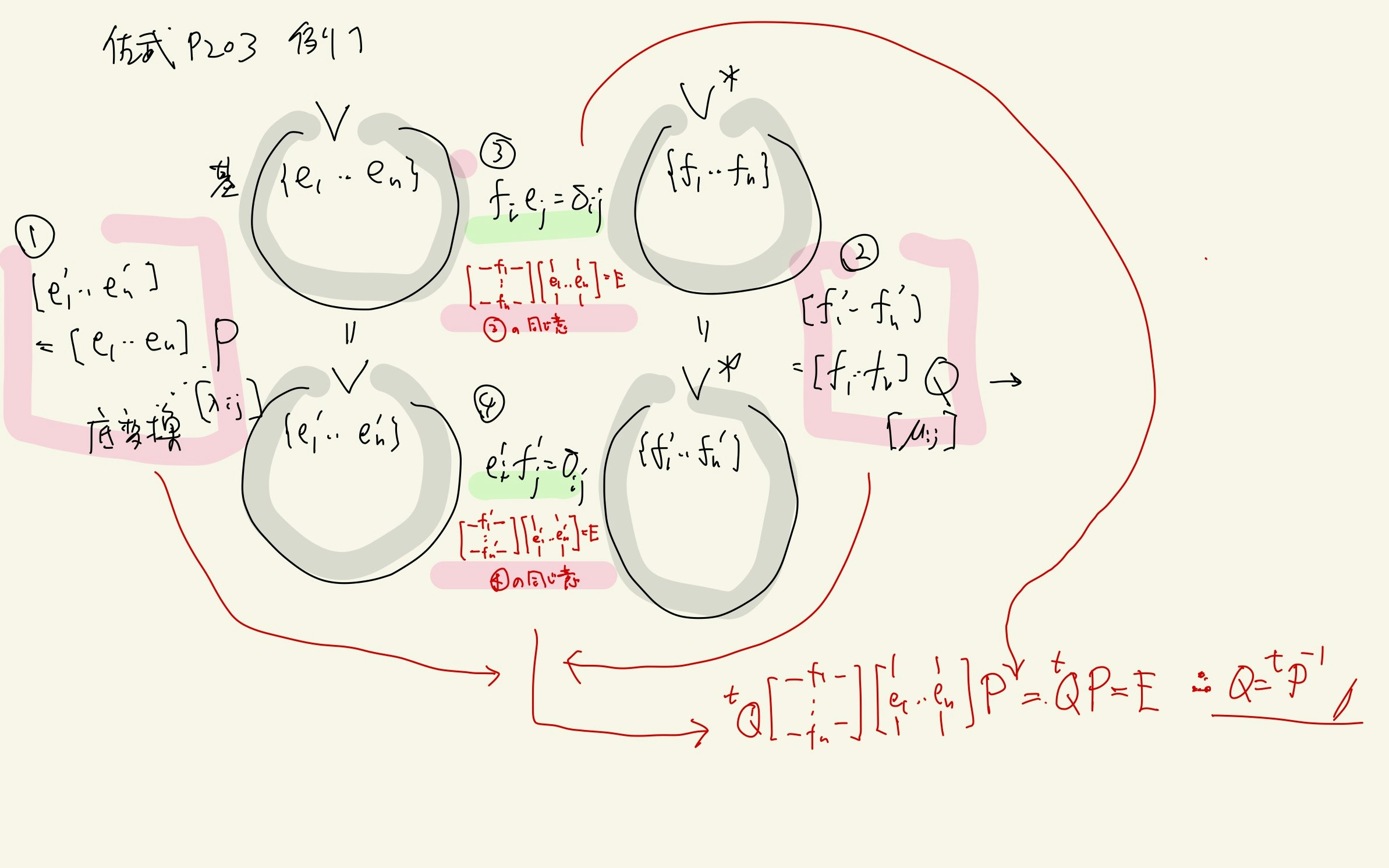
p.203 双対空間，再度簡略可視化と例1

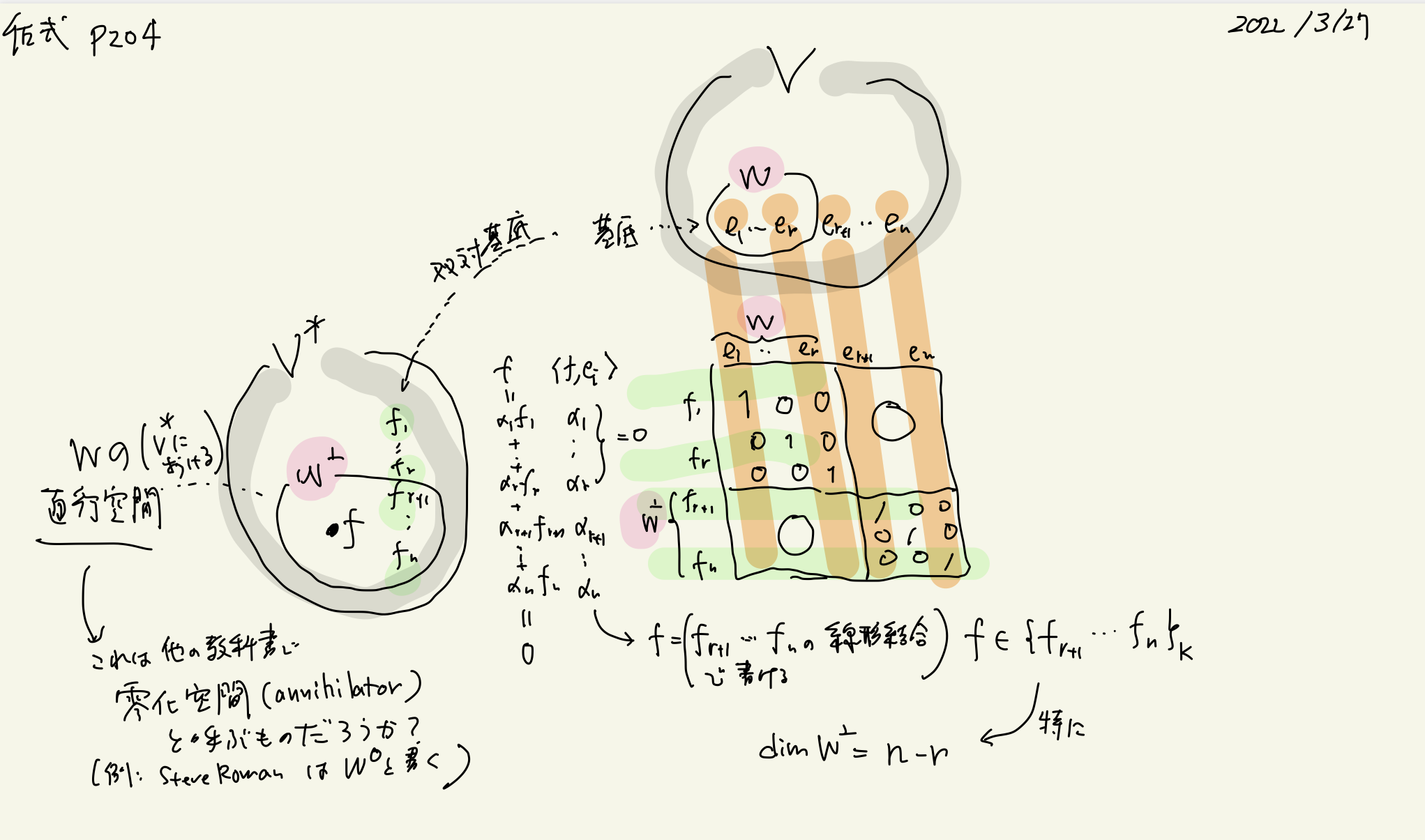
p.204 双対空間における直交空間

W^\perp = \{ f \in V^* ; <f,x> = 0 \quad \text{for all x} \in W \}

ここでの， $W^\perp$ は双対空間に存在します．Steven Roman 先生が annihilator と呼んでいるもの ($W^0$ と書く) を指していると思います．

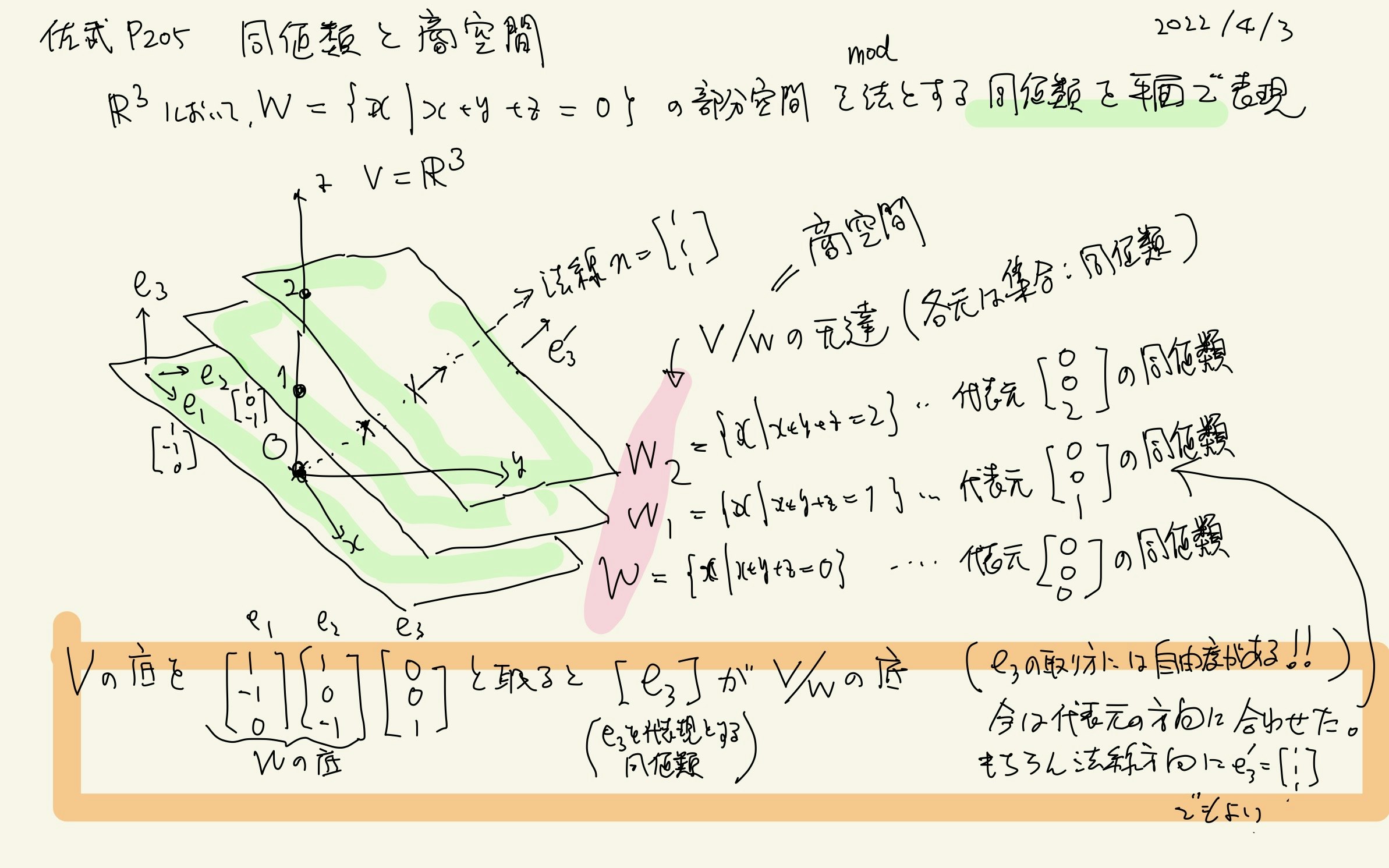
p.205 剰余類空間（商空間）

何度出てきても混乱する概念．整数の剰余との類似で覚えている．
商空間は「補空間の元が集合になる」というのが混乱する元なんだと思う．しかも，法となる部分空間に対して，その補空間を１つ決めるとその補空間の元が代表元になるのだが，補空間の取り方に自由度がある．図で言うと，z軸にとってもよいし，法線方向にとってもよい．

注意点として，

• 各同値類自体は，$V$の部分空間ではない！(最初の$W$のみが原点を含む部分空間)
• しかし，各同値類は商空間　$V/W$の元である．
• 商空間の元は「ベクトルの集合（同値類）」である
• 商空間はベクトル空間である．

最近，Steven Roman 先生の動画を見ていて，部分空間S(Subspace)に対して，各剰余類の代表元をすべて含むSの補空間TをTransversal と呼び，$V=S+T$ と直和分解することができる．

これを基礎に Vを格子に区切ると,群論のラグランジュの定理（Vの位数＝Sの標数*Sの位数)の類似(もしくはそのもの)となっていることに気づきました．

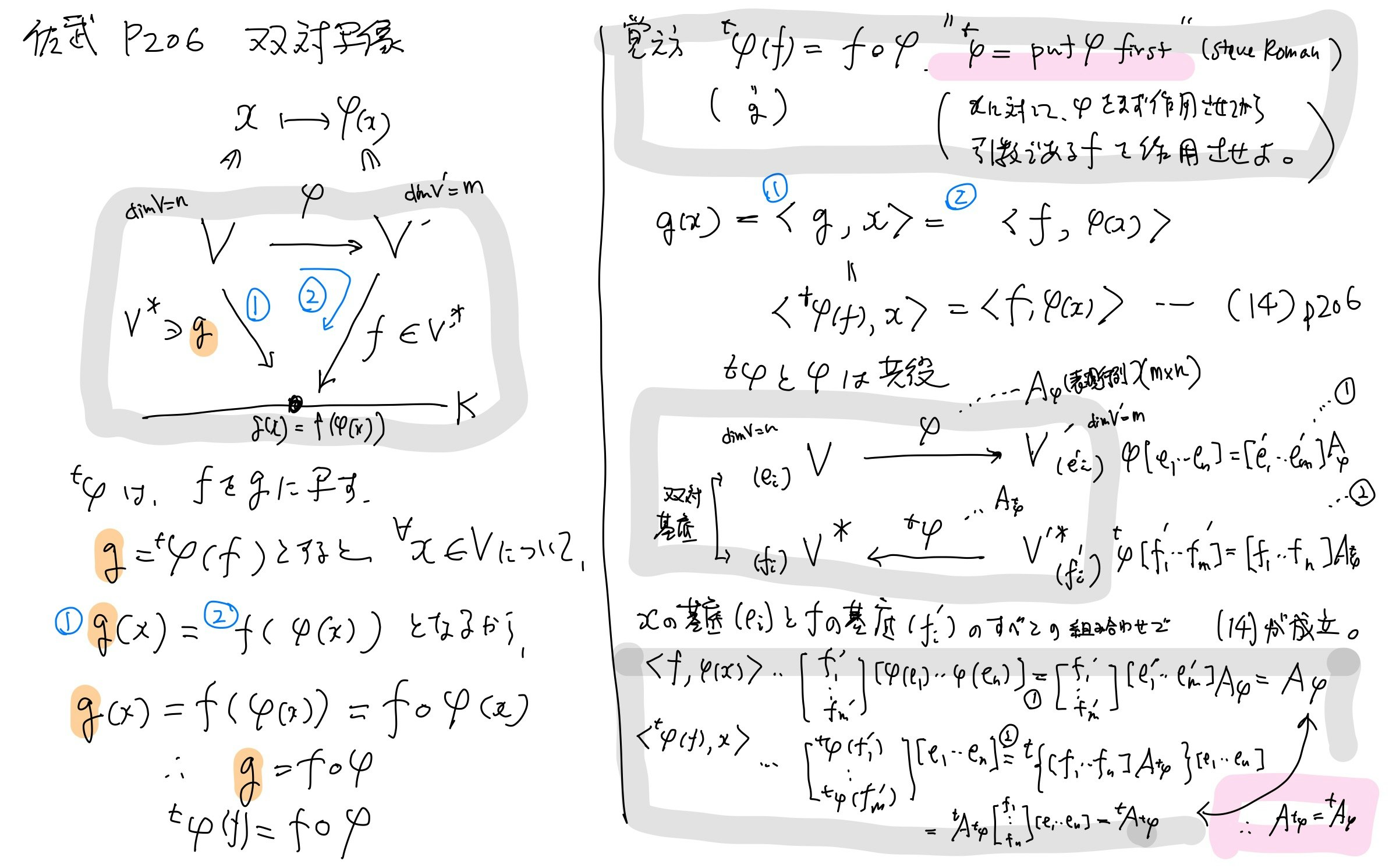
p.206 双対写像

ここは本当に難しい，，， Steven Roman 先生の動画を補助的に見ている． $^t\phi$ を "put $\phi$ first" と読み下して，引数である線形形式$f$に対して，$\phi$を掛けてから$f$を掛ける写像" という風に$f$を変換する，としている（直感的で覚えやすい）．

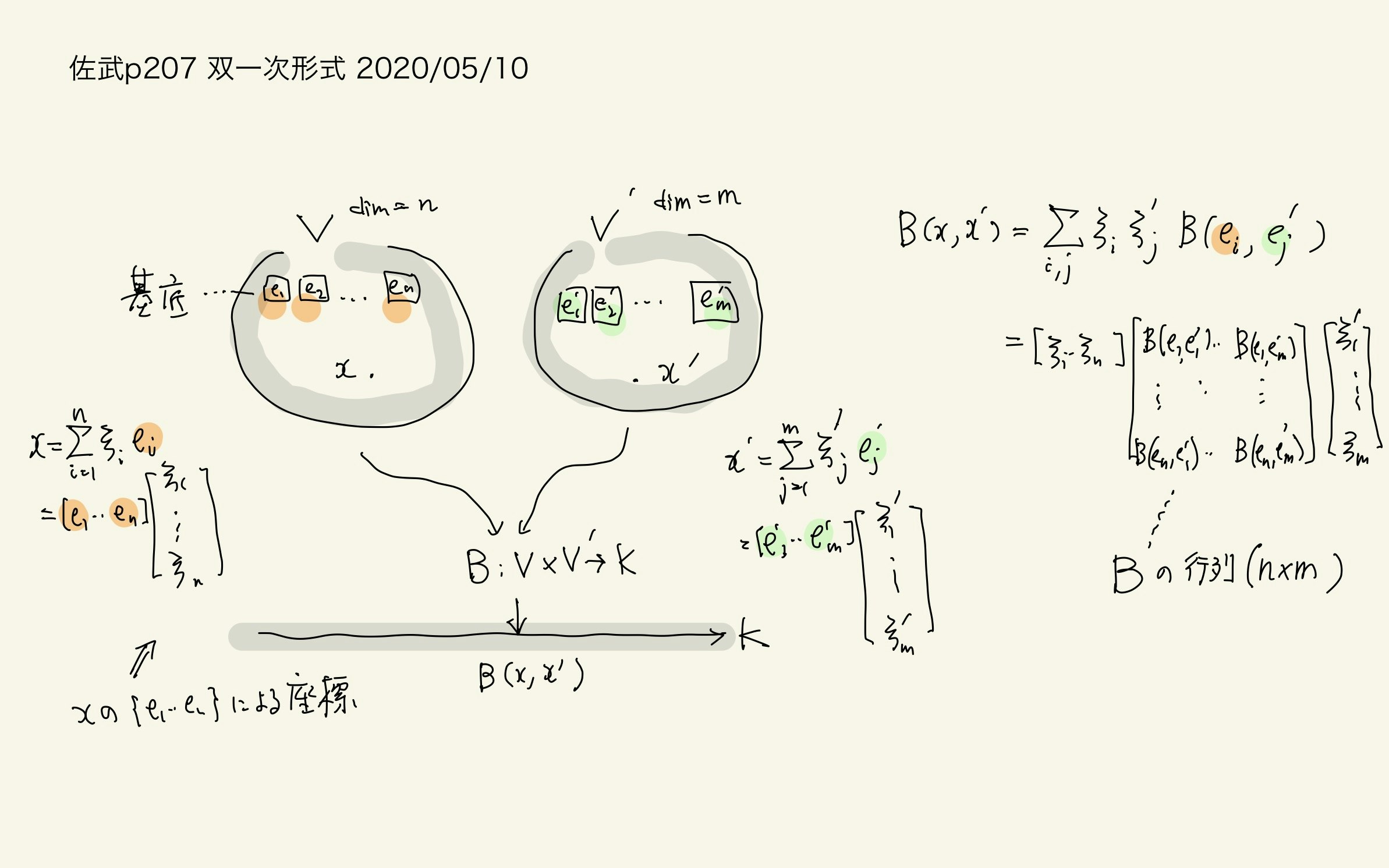
p.207 双一次形式

$B(x, y)$ の定義です． $x, y$ の両方について線形になる（一方を止めると一次函数）．

p.207-208 双一次形式

ここは特に苦労しました．

2つの $B$ が出てきて，一方は双一次形式であり，他方は $V'$ から $V^*$ への写像である．
それぞれの「行列」は，

• 前者: $B(e_i, e_j')$ を $(i,j)$要素に持つ「$B$の行列」
• 後者: $e_i', f_i$($e_i$ の双対基底)を底とする変換$B: V' \rightarrow V^*$の表現行列

で，それらが等しいと言っている．

p.212 一次写像の空間

ずっと，双対空間，双一次形式，と進んで，ついにテンソルが定義された．
うまく定義でき，その定義が一意である（カノニカルである）ことまで来た．

次に，一次写像全体 $V \rightarrow V'$ のなす空間 $\mathscr{L}(V,V') $　を $f\in{V^*}$ と $x' \in{V'}$ についてパラメータ化して， その元を $\phi_{x',f}: x \mapsto <f,x>x'$ としている．そして，これがテンソル積であると．

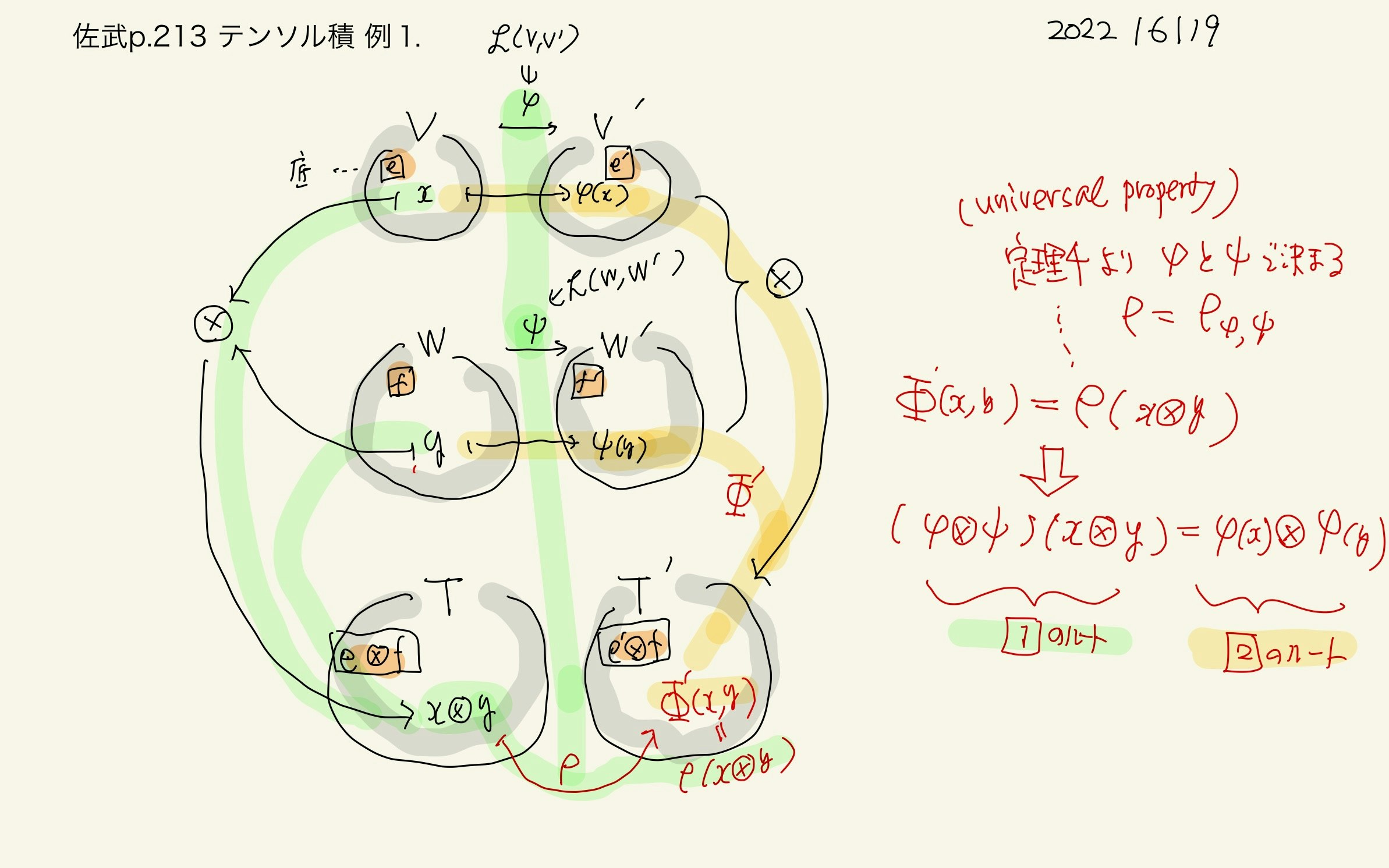
p.213 例1 行列のテンソル積

ずっと難しい状態が続いています．用語と繋がりだけ整理．

• $V \rightarrow V'$ のなす空間 $\mathscr{L}(V,V') $
• $W \rightarrow W'$ のなす空間 $\mathscr{L}(W,W') $

から，

• $\mathscr{L}(V,V') \otimes \mathscr{L}(W,W') $

を考え，普遍性から示しています．

• $\mathscr{L}(V,V') \otimes \mathscr{L}(W,W') = \mathscr{L}(V \otimes W,
  V' \otimes W')$

これを使って， 行列のテンソル積，$A \otimes B$ を定義します．

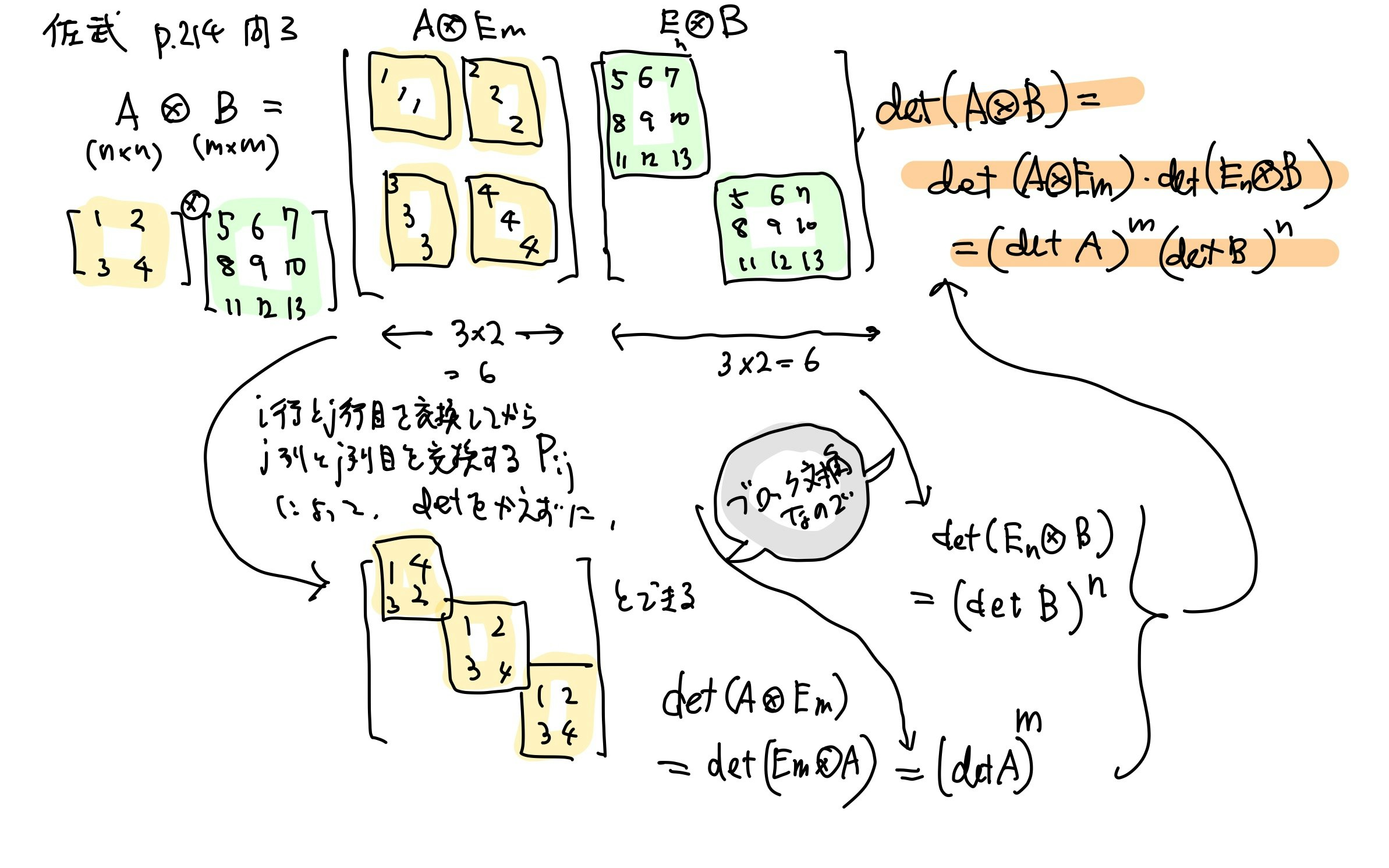
p.214 問3 テンソル積の行列式の値

数式を追うのが辛いので，具体で攻めてみた．なるほどなるほど．

p.202 テンソルの定義

テンソルの途中で迷子になってしまったので，再度，テンソルの定義に戻る．
まず，これが定義． 写像 $\Phi(x,y)$ はこの後で $x \otimes y$ と正式に認識される過程を踏む．

この定義の下の補題．$\Phi(e_i,f_j)$が $T$ の基底になることと，定義の(T1),(T2)の同値性．
まずは，十分性より．

証明の式を正確に追いたかったので，行列表記をして，$i,j,k,r$の大きさと整合性をチェックしている．

次に必要性．ここも教科書の記述をトレースしながら，言葉を補った．

ふぅ．難しい．

p.213　一次写像の空間

少し前戻りしました。一次写像 $\mathscr{L}(V,V')　= V' \otimes V^*$ を示した後で、このことに慣れる問題です。

$\quad \phi_{x\prime,f} : V \ni x \quad \rightarrow \quad <f,x>x' \in V' $

$V$の双対空間の元と、$V'$を使って写像を定義できる、という話です。$x$ から、$\lt f,x \gt$でスカラーに落とし、それを、$V'$の元 $x'$の方向倍率とします。理解のための練習演算。

（以下，順次追加していきます）