processingで綺麗な方程式を可視化する

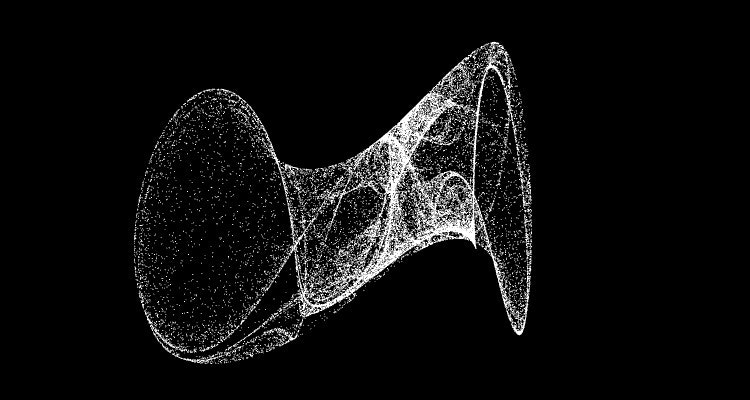
世の中には様々な数式が存在していてその中一つにClifford Attractorというものがあります
xn+1 = sin(a yn) + c cos(a xn)
yn+1 = sin(b xn) + d cos(b yn)
と非常にシンプルですが計算を繰り返す事でとても綺麗な数式です

ネットとかでsourcecodeがあるのか調べてみましたがなっかったので（もしあったらすいません...）
式を解析して書きました　独学なのでこの解析が正解どうかはわかりませんが

clifford_attractor.pde

int count=40000;

float x=1;
float y=1;
float z=1;

float a=1.4;
float b=1.6;
float c=1;
float d=1.7;

float xn;
float yn;
float zn;

float rotate_x;
float rotate_y;




float [][] points=new float[3][count];

void setup(){
size(750,400,P3D);

//xn+1= sin(a*yn)-c*cos(a*xn)
//yn+1= sin(b*xn)-d*cos(d*yn)
//zn+1= sin(xn)

for(int i=0;i<count;i++){
 
xn= sin(a*y)-c*cos(a*x);
yn= sin(b*x)-d*cos(d*y);
zn= sin(x);

x=xn;
y=yn;
z=zn;

points[0][i]=x*100;
points[1][i]=y*50;
points[2][i]=z*100;

}

}

void draw(){
background(#000000);
 fill(#FFFFFF);
translate(width/2,height/2);

rotateX(rotate_x);
rotateY(rotate_y);

for(int i=0;i<count;i++){
 pushMatrix();

  beginShape(POINTS);
  vertex(points[0][i],points[1][i],points[2][i]);
  endShape();

stroke(#FFFFFF);
popMatrix();
 
}

 rotate_x+=0.03;
 rotate_y+=0.03;

}

ちなみにZ座標の式zn= sin(x)は奥行きを出したかったので僕が適当に書いたものです
100行のないのでコピペして使って下さい
PVectorクラスやシェーダーなど使ってアニメーションさせたら面白いかもですね～。
参考サイト
http://paulbourke.net/fractals/clifford/