何を面白いと思っているか
ガウス過程回帰を実装して、色々と試していた。
import numpy as np
class GaussianProcess:
"""ガウス過程に基づいて予測してくれるやつ
"""
def __init__(self, x_line: np.ndarray = None, y_line: np.ndarray = None) -> None:
"""constructor
Args:
x_line (np.ndarray, optional): training data の x のほう. Defaults to None.
y_line (np.ndarray, optional): training data の y のほう. Defaults to None.
"""
self.x_line = x_line
self.y_line = y_line
# もし2つとも設定されているならば、 build してしまう。
if self.x_line is not None and self.y_line is not None:
self.build()
def build(self) -> None:
"""設定した x, y に基づいて、共分散行列と平均ベクトルを作る。
"""
self.cov = self.generate_cov()
self.mean = self.generate_mean()
def kernel_func(self, x1: float, x2: float) -> float:
"""kernel function の結果を返す。
今はデフォルトで rbf kernerl.
Args:
x1 (float), x2 (float): 求めたい x のペア
Returns:
float: kernel function の計算結果
"""
def rbf(x1: float, x2: float, p1: float = 1, p2: float = 1):
return p1 * np.exp(- ((x1 - x2) ** 2 / (2 * p2)))
return rbf(x1, x2)
def generate_cov(self) -> np.ndarray:
"""共分散行列を作る
Returns:
np.ndarray: 共分散行列
"""
result = []
for x1 in self.x_line:
result.append([self.kernel_func(x1, x2) for x2 in self.x_line])
return np.array(result)
def generate_mean(self) -> np.ndarray:
"""平均ベクトルを作る
Returns:
np.ndarray: 平均のベクトル
"""
# 今回は、 y そのものを平均とする
return self.y_line
def predicts(self) -> np.ndarray:
"""予測
Returns:
np.ndarray: 予測結果
"""
return np.array([*np.random.multivariate_normal(self.mean, self.cov)])
import random
from typing import Tuple
import numpy as np
class Sampler:
def __init__(self, f=None) -> None:
"""constructor
Args:
f (callable): R -> R の関数
"""
self.f = f
self.x_line: np.ndarray = None
def get_new_samples(self, sample_num: int = 10) -> Tuple[np.ndarray, np.ndarray]:
"""与えられた x の範囲からサンプルの列を返す
Args:
x_line (np.ndarray): np.arange(0, 10, 0.1) みたいなやつの結果
sample_num (int, optional): 得たいサンプルの数. Defaults to 10.
Returns:
Tuple[np.ndarray, np.ndarray]: サンプル。左から x, y
"""
# x_line よりも sample が大きければ sample とれないのでだめ
if len(self.x_line) < sample_num:
raise
# 得たい sample の数だけ x からランダムに数を選ぶ
selected_x_line = np.array(random.choices(self.x_line, k=sample_num))
return selected_x_line, self.f(selected_x_line)
def get_line(self) -> Tuple[np.ndarray, np.ndarray]:
"""曲線を返す
Returns:
Tuple[np.ndarray, np.ndarray]: 左から順に x, y
"""
return self.x_line, self.f(self.x_line)
# %%
import matplotlib.pyplot as plt
import numpy as np
from gp import GaussianProcess
from sampler import Sampler
# %%
# 今回の関数
def f(x: np.ndarray) -> np.ndarray:
return 1 - 1.5 + np.sin(x) + np.cos(3 * x)
# %%
# 今回は 0.01 刻みで -3 から 3 の間で。
x_line = np.arange(-3, 3, 0.01)
# Sampler を作る。
s = Sampler()
s.f = f
s.x_line = x_line
# ガウス過程回帰の準備
x_sample, y_sample = s.get_new_samples(sample_num=100)
gp = GaussianProcess(x_sample, y_sample)
# 予測する
y_result = gp.predicts()
# 描写
plt.plot(*s.get_line())
plt.plot(x_sample, y_sample, 'o')
plt.plot(x_sample, y_result, '+')
plt.show()
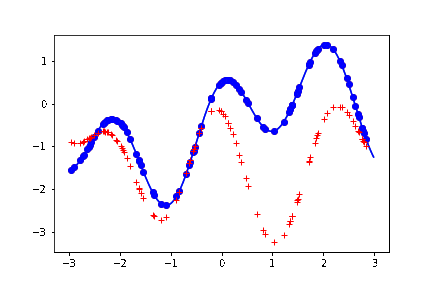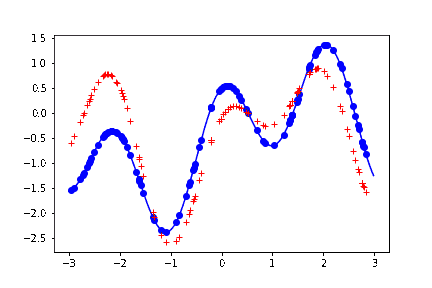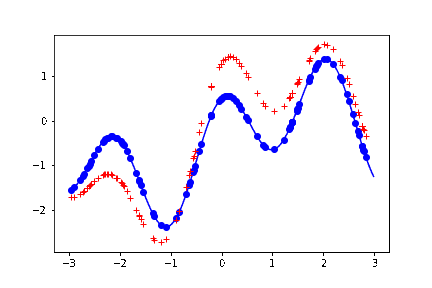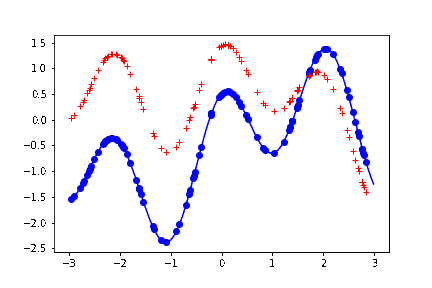
結果。上の最後の描写のブロックを何回か叩く度に、以下のように、曲線めいたものが生成される。
薄い青色の実線が、生成もとの関数。つまり予測した結果はこの関数の形に近ければ近いほど嬉しい。
青い丸点が、この関数から生成したサンプル。この議論では本質ではないため、ノイズは載せていない。
赤い + の点が、予測した結果。
赤い + の点の並びを、目を薄めながら見ると、曲線に見える。実際この直感な変でもなくて、参考文献にあげた教科書には、ガウス過程回帰を「振ると関数がランダムに出力される箱」みたいに表現している。
これが面白いと思った。その真意を説明する。
まず「振ると関数がランダムに出力される箱」自体は、ガウス過程回帰に限った現象ではない。例えば、以下のような線形基底関数のモデルを考える。
$$
y = \sum w \phi (x)
$$.
ここで各 $w$ を、それぞれある確率分布に従う確率変数と考える。するとこれは「振ると関数がランダムに出力される箱」と言うことができるだろう。
そうなんだけど、さらに踏み込んで考えたい。この「振ると関数がランダムに出力される箱」の中身を考えると、大きく以下2つのステップに分かれる:
(1) 各 $w$ それぞれに、ランダムに値を決める。
(2) (1) で決めた値を代入して、曲線を出す。 → ランダムな曲線が出力される。
ここで話をガウス過程回帰に戻す。
ガウス過程回帰の体験として面白いのは、上のステップに寄せた説明をすると、ざっくり以下のようになるところ:
(1) 各 $x$ それぞれに、ランダムに値を決める。 → ランダムな曲線(めいたもの)が出力される。
実際、実装を見てもらうとわかるように、予測の点列は、多次元の正規分布からサンプリングしたものである。
def predicts(self) -> np.ndarray:
"""予測
Returns:
np.ndarray: 予測結果
"""
return np.array([*np.random.multivariate_normal(self.mean, self.cov)])
ここで np.random.multivariate_normal は多次元の正規分布を意味している。また mean, cov はそれぞれ平均のベクトル、共分散行列を意味している。
つまり体験としては、「各点を多次元の正規分布に基づいて値を取り出したが、それがたまたま曲線のように見える、ということが常に起きている」というかんじ。この「たまたま」感とそれが「常に」起きているところが共存しているかんじが、なんとなく面白く感じている。
これを説明する 3 つのアイディア
以下では、そんな「たまたま」なことが「常に」起きることを説明しようとする 3 つのアイディアを紹介する。
これらは、ひょっとしたらいずれか一つで納得することができるかもしれないし、 3 つともつまるところだいたい同じことを言っているかもしれない。そうした曖昧さを含む 3 つのアイディアを紹介する。
1. 共分散行列の構成方法を見る
ちょっと具体的に、上の実装の中身を説明する。
平均のベクトル mean は、トレーニングデータを $\mathcal{D} = \{{ (x_i, y_i) \}}$ とした場合のベクトル $(y_i)$ そのもの。
共分散行列 cov は、各 $x$ のペア $x_i, x_j$ に対して、以下のガウスカーネルを通して計算して求めたものである。下の式は、ガウスカーネルの諸々のハイパーパラメータを 0 なり 1 を代入して本質的な部分だけを残したもの:
$$
k(x_i, x_j) = \exp (-( x_i - x_j )^2)
$$.
この共分散行列の構成方法に注目したい。
わかりやすく、極端な例で考える。 training data が $x_i$ と $x_j$ の 2 点しかないとしよう。このとき、共分散行列は以下の 2 次の正方行列となる:
\left(
\begin{matrix}
k(x_i, x_i) & k(x_i, x_j) \\
k(x_j, x_i) & k(x_j, x_j)
\end{matrix}
\right)
この共分散行列は、実は特徴的な形をしている。
まず、ガウスカーネルの式の形から、 $k(x_i, x_j) = k(x_j, x_i)$ である。つまり、上の行列は対角行列であることがわかる。
さらに、これまたガウスカーネルの式から、 $k(x_i, x_i) = k(x_j, k_j) = 1$ である。つまり、上の行列は対角成分がすべて 1 である。
これらを考慮すると、このように構成した共分散行列は、定数の $a$, $b$ を用いて、以下のような形をしていることになる。
\left(
\begin{matrix}
a & b \\
b & a
\end{matrix}
\right)
$a$ は厳密には 1 なのだけれども、以降の議論には影響がない & より一般的な結果を述べるために、文字をおいておく。
さて、このタイプの共分散行列を持つ 2 次元の正規分布は、特徴的な形をしている。それを説明する。
この共分散行列の精度行列を考える、が、結局同じような形になっているので、ここからは、上の $a$, $b$ からなる行列をそのまま精度行列とみなして話をすすめる。
上の精度行列を対角化する。普通にやると固有値を求めて〜という手段を使うけれども、今回は答えがわかっているので、固有値を以下のように置く:
\lambda_1 = a - b, \ \lambda_2 = a + b.
すると上の精度行列は以下のように対角化できる:
\begin{align}
\left(
\begin{matrix}
a & b \\
b & a
\end{matrix}
\right)
&=
\left(
\begin{matrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
- \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{matrix}
\right)
\left(
\begin{matrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{matrix}
\right)
\left(
\begin{matrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
\cos \frac{\pi}{4} & -\sin \frac{\pi}{4} \\
\sin \frac{\pi}{4} & \cos \frac{\pi}{4}
\end{matrix}
\right)^{-1}
\left(
\begin{matrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{matrix}
\right)
\left(
\begin{matrix}
\cos \frac{\pi}{4} & -\sin \frac{\pi}{4} \\
\sin \frac{\pi}{4} & \cos \frac{\pi}{4}
\end{matrix}
\right) .
\end{align}
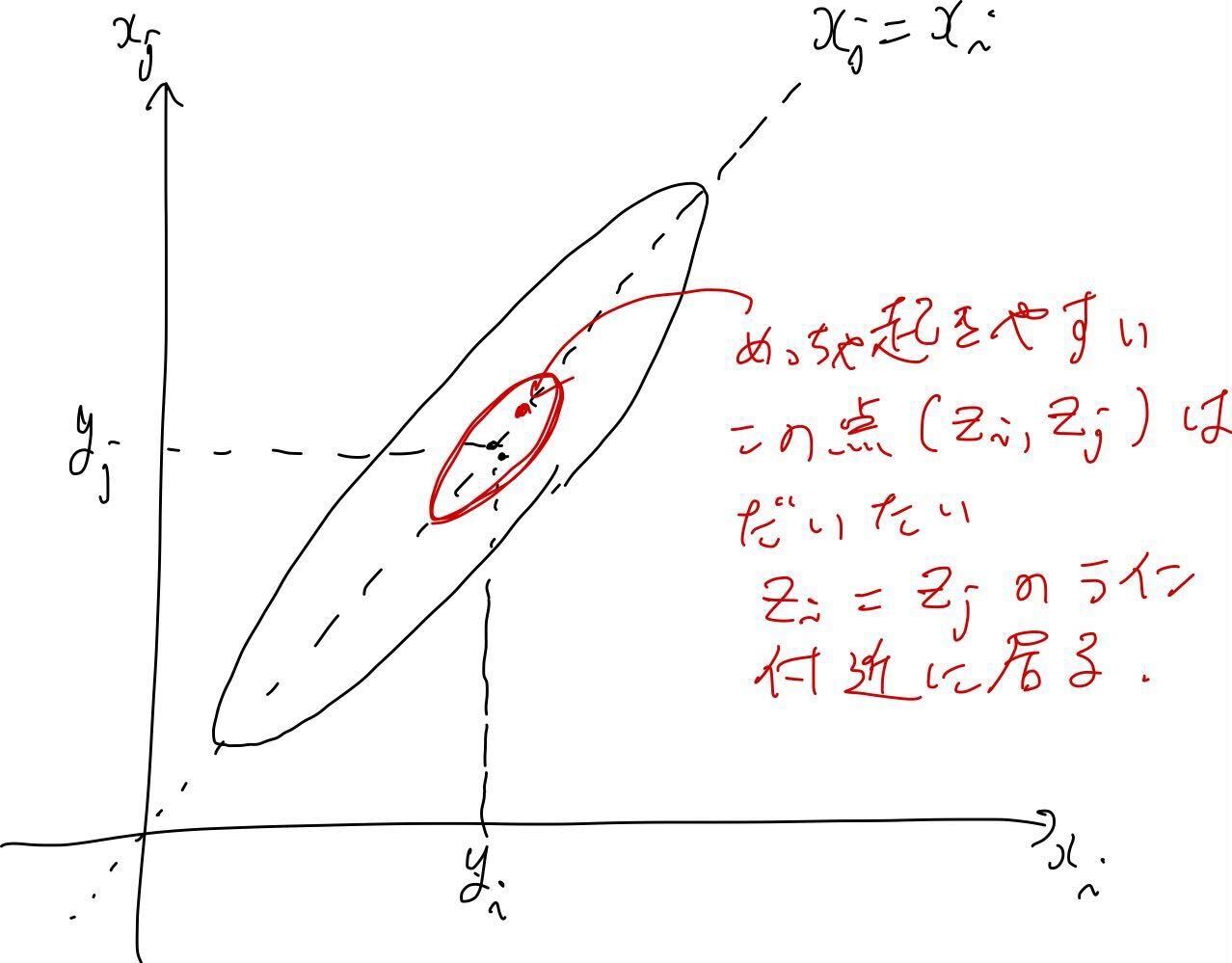
これは即ち、雰囲気で表現するけれど、この 2 次元の正規分布を上から眺めたときに、右斜め 45 度に傾いた楕円形になってるかんじ。つまり、平均を通る $y=x$ のラインに近い点が起きやすい。
さらに、 $x_i$ と $x_j$ がめちゃくちゃ近い値であるとすると、ガウスカーネルの値は最大値の 1 に近づく。これは即ち、 $x_i$ と $x_j$ の共分散が大きくなることを意味する。
さらにさらに、$x_i$ と $x_j$ それぞれに対応するデータ $y_i$, $y_j$ は、 $x_i$ と $x_j$ がめちゃくちゃ近ければ、$y_i$, $y_j$もまた近い値をとっているだろう、という直感を前提にする。
以上を総合的に鑑みると、以下のようなことになる:
「$x_i$ と $x_j$ が十分に近いなら、上のようにして構成した 2 次元の正規分布から抽出したサンプル $z_i, z_j$ は、だいたい近い値になっている。」
絵に書くとこんなかんじ:
これが、すべての近い $x$ のペアで起きていると考えると、ランダムに取り出したやつがなぜいつも近くにいるのか?ということが、なんとなくしっくり来る。
2. 線形基底関数モデルから考える
ここでは、線形基底関数モデル:
y = \sum w \phi(x)
を出発点に考えていく。
training data $\mathcal{D} = \{{ (x_i, y_i) \}}_{1}^{N}$ に対して、うまく fit している線形基底関数モデルの式を考えると、およそ以下のことが成り立つ。ここでは簡単のため、ノイズを考えない。
\begin{align}
\left(
\begin{matrix}
y_1 \\
y_2 \\
\vdots \\
y_N
\end{matrix}
\right)
&=
\left(
\begin{matrix}
\phi_1 (x_1) & \phi_2 (x_1) & \dots & \phi_M (x_1) \\
\phi_1 (x_2) & \phi_2 (x_2) & \dots & \phi_M (x_2) \\
\vdots & \vdots & \ddots & \vdots \\
\phi_1 (x_N) & \phi_2 (x_N) & \dots & \phi_M (x_N) \\
\end{matrix}
\right)
\left(
\begin{matrix}
w_1 \\
w_2 \\
\vdots \\
w_M
\end{matrix}
\right).
\end{align}
ここで上の表記をベクトルと行列の記号一文字ずつで表現したものを以下のようにしておく:
\mathbf{y} = \Phi \mathbf{w}.
んで、ここで $\mathbf{w}$ がある正規分布に従うとしよう。
\mathbf{w} \sim N(\mathbf{0}, E) .
$E$ は単位行列。平均も全部 0. つまり説明のために色々なものを簡略化している。
この仮定は、この記事の冒頭に述べたものである。すなわち、
- (1) 各 $w$ それぞれに、ランダムに値を決める。
- (2) (1) で決めた値を代入して、曲線を出す。 → ランダムな曲線が出力される。
という2つのステップを踏んで曲線をランダムに抽出する、より直感的なかんじを想定している。
さて、 $\mathbf{w}$ が正規分布に従うなら、その定数行列 $\Phi$ による行列操作によって得られた $\mathbf{y}$ もまた正規分布に従う。
では $\mathbf{y}$ の共分散行列や平均はどうなっているか?
まず平均は、
\begin{align}
E[\mathbf{y}] = E[\Phi \mathbf{w}] = \Phi E[\mathbf{w}] = \mathbf{0}.
\end{align}
次に共分散行列は、
\begin{align}
E[\mathbf{y} \mathbf{y}^T] - E[\mathbf{y}]E[\mathbf{y}]^T &= \Phi E[\mathbf{w} \mathbf{w}^T] \Phi^T \\
&= \Phi \Phi^T.
\end{align}
つまり、
\mathbf{y} \sim N (\mathbf{0}, \Phi \Phi^T).
ここで、共分散行列 $\Phi \Phi^T$ の各成分に注目する。 $\mathbf{\phi} = (\phi_1, \phi2, \dots, \phi_M)^T$ とするならば、共分散行列の $(i, j)$ 成分は、 $\mathbf{\phi} (x_i)^T \mathbf{\phi} (x_j)$ となる。
ここで、この $\mathbf{\phi} (x_i)^T \mathbf{\phi} (x_j)$ が、ガウスカーネル $k(x_i, x_j)$ と表現されると仮定する。すると、平均は全部0という細かい違いはあるものの、今回の実装方法を表現した式になる。
つまり何が言いたいかというと、このように考えると、記事の冒頭でも述べた以下のステップ:
- (1) 各 $w$ それぞれに、ランダムに値を決める。
- (2) (1) で決めた値を代入して、曲線を出す。 → ランダムな曲線が出力される。
というのと、やっていることは本質的に変わらないよ、ということ。
3. ヒルベルト空間で考える
ここのセクションは本質的には完成していない。しかしながら、ここが完成すればかなり見通しのよい視点を得られるであろう。
これからヒルベルト空間の超説明をする。
僕らは N 次元のベクトル空間というのを既に知っている。それを N 次元の実ベクトル空間と呼ぼう。
単純に N = 2 の場合を考えよう。つまり(2 次元の)実ベクトル空間とは何であったか。
まず、ベクトルの元は $\mathbb{R}^2$ に属している。そして内積の演算
(\mathbf{a}, \mathbf{b}) = \sum a_i b_i
が定義されている。その内積を用いれば距離
|| \mathbf{a} || = \sqrt{(\mathbf{a}, \mathbf{a})} = \sqrt{\sum a_i^{2}}
が定義できる。
この雰囲気を、 別の空間でも考えてみる。ここから話が一気に抽象的で、いい加減になる。
以下のような空間を $L_2$ 空間と呼ぼう:
L_2 := \{ f; \int |f(x)|^2 dx < \infty \}.
雰囲気でしか説明しない。$f$ はよくある実数関数とでも考えれば OK。要するに $L_2$ はある性質を持った関数の集まり、くらいに感じておく。
この空間で、以下のような演算を内積と呼ぼう:
(f, g) := \int f(x) \bar{g} (x) dx.
実際、これはちゃんと確かめれば内積の定義を満たす。
このかんじで、この空間の中に距離を定義する。
|| f || := \sqrt{\int |f|^2 dx}.
まあこんなかんじで、実ベクトル空間 $\mathbb{R}^2$ 成立している諸々の性質を、 $L_2$ 空間 でも同じようなかんじで考えることができる。実は、この $L_2$ 空間はヒルベルト空間の一つである。ちなみに、この $L_2$ 空間がヒルベルト空間であることを厳密に示すのは、測度論を勉強した後の練習問題というかんじでそこそこ難しい。
ここで、ヒルベルト空間、ここでは $L_2$ 空間は、無限次元のベクトル空間と呼ばれることががある。なぜそのように言いたくなるのかを説明する。
実ベクトル空間の次元は、そのベクトルの基底の個数と一致する。基底というのは特殊なベクトルのことで、そのベクトルの線形結合で、その空間のすべてのベクトルを表現できる、そんな特殊なベクトルのことを意味する。例えば 2 次元の実ベクトル空間であれば、基底として $(1, 0)^T$ と $(0, 1)^T$ の2つを考えれば、 $\mathbb{R}^2$ のすべてのベクトルを、その2つの線形結合で表すことができる。
さて、 $L_2$ の基底はどのようなものがあるか?
その一つはフーリエ級数展開を思い出すとよい。
f(z) = \sum_{n=- \infty}^{\infty} c_n e^{inz}.
これは、関数 $f$ が $\{{ e^{int} \}}$ の線形結合で表現されていることを意味する。
これをベクトルを意識した言い方に直すと、(正規直交)基底 $\{{ e^{int} \}}$ の線形結合で $f$ が表現されている、というかんじ。
このとき基底は何個あるか? 無限個ある。これが無限次元のベクトル空間と呼びたくなるイメージ。
最後に一つ、汎関数について言及しておく。
汎関数は、 $L_2 \rightarrow \mathbb{C}$ となる関数のこと。つまり、関数 $f$ を引数にとる実数値の関数のイメージを持てば OK.
この汎関数が最大(あるいは最小)になるような関数 $f$ はなーんだ、みたいな問題のことを変分原理と呼んだりする。最小二乗法なんかは、広い意味で変分原理の一つ。
さて、なぜこのような空間を定義したくなったか。
それは、この $L_2$ 空間で確率を定義することによって、「振ると関数がランダムに出力される箱」というものが、そのまま表現されるから。
実際、実数の空間で定義したときと同じく、 $L_2$ 上の位相を用いて自然に確率測度を定義できる。
もう一つ重要なことが、リースの表現定理と呼ばれる有名な結果を用いることで、 $L_2$ のある部分空間の中で、ガウスカーネル $k$ を用いることによって、 $\mathbb{R}$ 上の点列 $x_n$ を、 $L_2$ 上の関数列 $k_{x_n}$ にマッピングすることができる。このアイディアを使うことで、 $\mathbf{R}$ 上では複雑怪奇な線形基底関数であるものが、 $L_2$ 上だと単純な単回帰のように捉えられるようにしたテクニックが、いわゆるカーネル法である。
ではガウス過程が $L_2$ 上でどのように具体的に構成されるのか。それはまだ考えてない。
追記: これ が関連するものかもしれない。