母平均の検定
「XXの平均とYYの平均」について,2つの平均の間には「差がある」のかどうかを検定する.
帰無仮説は「平均に差がない」,対立仮説は「平均には差がある」
- 独立な2群のt検定
- 対応のない2群のt検定(2つの母集団の分散が等しいと仮定できる場合):スチューデントのt検定
- 対応のない2群のt検定(2つの母集団の分散が異なると仮定できる場合):ウェルチのt検定
- 対応のある2群のt検定
- 調査の被験者が同じで,異なる複数の測定が行われた時
スチューデントのt検定の条件
- 標本抽出が無作為に行われていること
- 母集団の分布が正規分布に従っていること
- 2つの母集団の分散が等しいと仮定できること
この時,2つの母集団それぞれの標本を取り出したときの標本平均の差の分布は,次のようになる
\bar{x_1} - \bar{x_2} \ \~ \ N(\mu_1 - \mu_2, \sigma^2(\frac{1}{n_1} + \frac{1}{n_2}))
これを標準化すると
\frac{\bar{x_1} - \bar{x_2} - (\mu_1 - \mu_2)}{\sigma\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \~ N(0, 1^2)
標準正規分布に従うようになる.分母にある未知の母標準偏差σは次の式で推定できる.
\widehat{\sigma}_{pooled} = \sqrt{\frac{(n_1 - 1)\hat{\sigma_1}^2 + (n_2 - 1)\hat{\sigma_2}^2}{n_1 + n_2 - 2}}
$\hat{\sigma_1}^2$と$\hat{\sigma_2}^2$はそれぞれ群の不偏分散を,$n_1$と$n_2$はそれぞれ群のサンプルサイズを示している.
検定統計量tの実現値は
t値 = \frac{\bar{x_1} - \bar{x_2}}{\sqrt{\frac{(n_1 - 1)\hat{\sigma_1}^2 + (n_2 - 1)\hat{\sigma_2}^2}{n_1 + n_2 - 2} (\frac{1}{n_1} + \frac{1}{n_2})}}
例題
ある外食チェーンで,主力メニューを10人に試食してもらい,基準値を50点とする100点満点で採点してもらった.別の8人にはライバル店の主力メニューを食べてもらい,採点してもらった.主力メニューの平均点が77.5点,ライバル店の平均が82.5点だった.この平均に差があるか?
data <- read.csv("./r_sample/chap07/sec02/mean_difference_s/採点.txt", header=T)
menu1 <- data$当店
menu2 <- data$ライバル店[!is.na(data$ライバル店)] #欠損値を除いてベクトルに代入
mean_menu1 <- mean(menu1)
mean_menu2 <- mean(menu2)
pool <- sqrt( # poolされた標準偏差
(
(length(menu1) - 1) * var(menu1) +
(length(menu2) - 1) * var(menu2)
)
/ (length(menu1) + length(menu2) - 2)
)
# 統計検定量t値の分母の計算
dn <- pool * sqrt(1 / length(menu1) + 1 / length(menu2))
# 統計検定量の実現値を求める
st <- (mean_m1 - mean_m2) / dn
# 自由度
dof <- length(menu1) + length(menu2) - 2
# 自由度がサンプルサイズの合計 - 2 のt分布における下側確立0.025のt値を求める
t_low <- qt(0.025, dof)
t_upp <- qt(0.025, dof, lower.tail = FALSE)
curve(dt(x, dof), -3, 3)
abline(v=qt(0.025, dof))
abline(v=qt(0.975, dof))
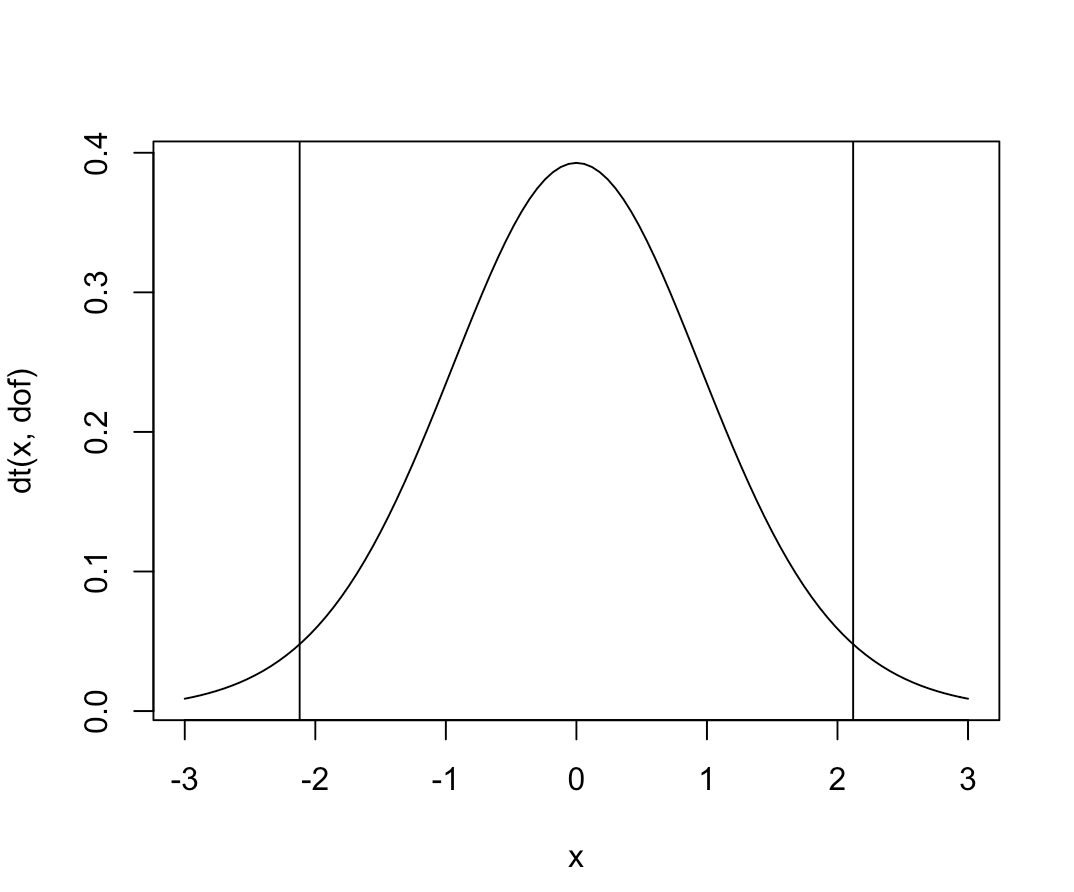
統計検定量t値の実現値は-1.57だった.棄却域に入っていないので,帰無仮説の「2つの商品の平均点には差がない」を採択する.
p値を求めてt検定を行う
p値とは,帰無仮説が正しいという仮説のもとで,「標本から計算した検定統計量の実現値以上の値が得られる確率」のこと.
p <- 2 * pt(st, dof)
# stは検定統計量,dofは自由度
# 0.133... で0.05より大きいので,帰無仮説を棄却.平均に有意な差はない.
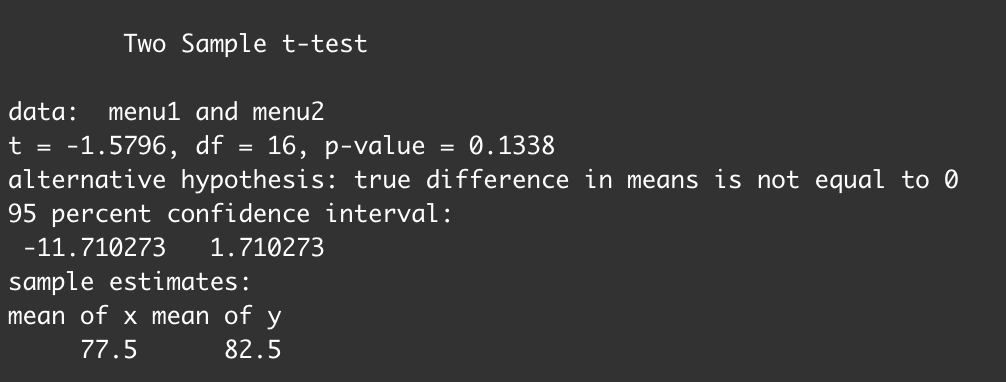
t.test()関数で検定統計量t値の実現値を求める
t.test(data1, data2[, var.equal=T])
var.equal=Tでスチューデントのt検定を行う
t.test(menu1, menu2, var.equal = T)