Learning to Rank with Implicit Feedbackに関するまとめ

Learning to Rank with Implicit Feedback

Unbiased Learning to Rankについて勉強したので、その内容についてまとめます。

本記事はSIGIR2019のTutorial SessionであるUnbiased Learning to Rank: Counterfactual and Online Approachesをベースにまとめております。

構成は、はじめに、Learning to RankをImplicitデータで行うことのメリットとデメリットについて述べます。
その後にデメリットを解決するための手法に関して、Counterfactual Learning to Rank, Online Learning to Rankのそれぞれを具体例を交えて説明します。
最後にCounterfactual Learning to RankとOnline Leaning to Rankの精度を比較した論文について紹介します。

はじめに

Learning to Rank (LTR）について

Learning to Rankとは、User+Itemの情報から、Itemの並び順を推定するための機械学習の手法のことを総称したものです。

検索結果の一覧の並び順を作成するために主に使用されています。

並び順の学習の仕方から、大きく分けてPointwise, Pairwise, Listwiseの3つの手法が存在します。本記事ではそれらに関する詳しい説明はしませんが、下記リンク先の説明がわかりやすいです。

入力データには、クエリの特徴や並び順を決めるItemの特徴などが使用され、予測するのは、クエリごとの正解の並び順になります。

論文でよく使用されているデータセットには、Yahooのデータセットなどがあります。

このようなデータセットには、クエリ×アイテムごとにperfect(4), excellent(3), good(2), fair(1), bad(0)などの人手の正解スコアが付与されており、このスコアが高い順に並び順を推定するようなモデルを作成することがLTRのタスクとなります。

Learning to Rank with Explicit Feedbackのイメージ図

|

人手で付与された正解データのことをExplicit Feedbackと呼びます。Explicitなデータを用いるのは、「アノテーションのためのコストがかかり、大量の正解データを取得するのが難しい」という課題が存在します。

そこで、ユーザのオンライン上でのクリックデータを元に並び順を学習するという方法が考えられます。このようなクエリ×アイテムごとのアイテムがクリックされたか、されてないかというデータのことをImplicit Feedbackと呼びます。

Implicitなデータを用いることで、大量の学習データを用意することができるのですが、次に述べるような課題が存在します。

Implicitデータを用いることの課題について

Implicitなデータには様々なバイアスが含まれています。このバイアスを考慮せずに学習すると意図した並び順の学習ができないといった課題が存在します。

ここでは主にPosition Biasについて説明します。

Implicitなデータを元に学習を行う場合、クリックされたアイテムをより上位に、クリックされなかったアイテムを下位に表示するようなモデルを作成することが目的となります。

しかし、ここにPosition Biasという問題が存在します。Position Biasとは簡単にいうと、上位に表示されたアイテムは下位に表示されるアイテムよりもクリックされやすいというバイアスのことです。

ユーザの視覚のヒートマップ	ユーザのクリックモデル
http://ltr-tutorial-sigir19.isti.cnr.it/slides/

上記の左の図は、Webページ上のユーザの閲覧した箇所のヒートマップを表しています。
この図より、ユーザは上位にあるアイテムにより注目しているということがわかります。

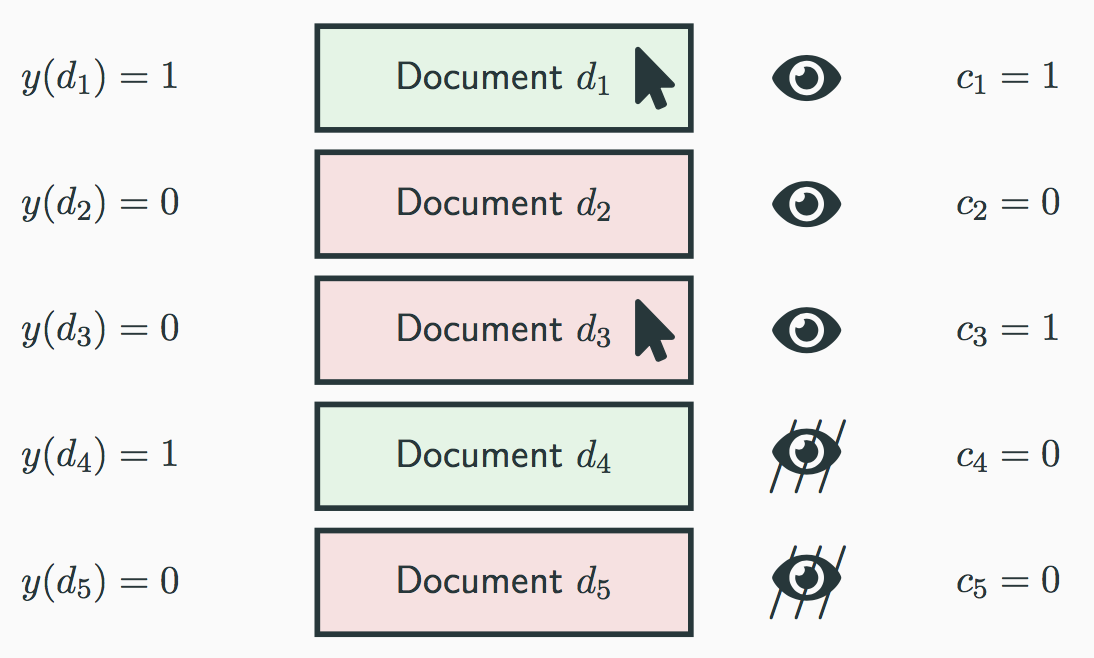
ユーザのこのような特徴により、受けるPosition Biasを図示したものが右の図になります。
右図の$c_k$は$k$番目の位置で表示されたアイテムがクリックされたかされていないか（1 or 0）を表しています。
また、$y(d_k)$は$k$番目に表示されたアイテム$d_k$がユーザにとって興味のあるものかないものか（1 or 0)を表しています。

本来的には$y(d_k)$が1のアイテムを上位に、0のアイテムを下位にするようなモデルの学習を行いたいのですが、Implicitなデータ（アイテムのクリックデータ）には、図中の$d_4$のような、ユーザに閲覧されなかったことにより、クリックされないアイテムが存在します。

何も考えずにImplicitなデータより並び順の学習を行うと、本当は上位に表示したいのに、ユーザに閲覧されずクリックされなかったアイテムは下位に表示されるようなモデルができてしまいます。
このようなバイアスのことをPosition Biasと呼びます。

課題について簡単にまとめると、Implicitなデータを使用する場合、Position Biasを考慮しないと、学習データ中で上位に表示されていたアイテムが上位に出やすいようなモデルが出来上がってしまいます。

このようなバイアスを考慮しながらImplicitなデータより並び順の学習ができるモデルの枠組みとして、Counterfactual Learning to Rank, Online Learning to Rankの２種類が存在します。

それぞれのモデルの考え方、具体的な手法について以降の章で説明していきます。

Counterfactual Learning to Rank (CLTR)

本章ではCounterfactual Learning to Rank (以降CLTRと略する)に関する基本的な考え方について説明します。

ロジック概要

ここではUnbiased Learning-to-Rank with Biased FeedbackをベースにCLTRの基本的な考え方について説明します。

まず、CLTRの前提にあるクリックモデルという考え方について説明したのちに、CLTRで最大化したい指標について説明します。

クリックモデル

CLTRでは、ImplicitデータからPosition Biasを考慮した並び順を学習するために、まずユーザのクリックのモデルリングを下記式のように行います。

P(c_i=1 \land o_i=1|y(d_i),R) = P(c_i=1|o_i=1,y(d_i))P(o_i=1|R, d_i)

ここで、$R$はあるクエリでのアイテムのランキング、$d_i$はその時の$i$番目に表示されたアイテム、$c_i \in \{0, 1\}$は$i$番目に表示されたアイテムがクリックされたかどうか、$o_i \in \{0, 1\}$は$i$番目に表示されたアイテムが閲覧されたかどうか、$y(d_i) \in \{0, 1\}$はアイテム$d_i$がユーザにとって興味のあるアイテムであるかどうかを表しています。
また、$P(o_i=1|R, d_i)$はクエリ$R$で$i$番目に表示されたアイテムが閲覧される確率、$P(c_i=1|o_i=1,y(d_i))$はアイテム$d_i$が閲覧された時にクリックされる確率を表しています。

LTRの正解データとして使いたいのは、$P(c_i=1|o_i=1,y(d_i))=y(d_i)$（興味がないアイテムはクリックされないと仮定した場合）です。
しかし、$P(c_i=1|o_i=1,y(d_i))$はImplicitなデータから観測することはできず、実際に観測できるのは、$P(c_i=1 \land o_i=1|y(d_i),R)$（アイテムがクリックされる確率）です。

CLTRの学習では、$P(c_i=1 \land o_i=1|y(d_i),R)$から$P(o_i=1|R, d_i)$（アイテム$d_i$が閲覧される確率）を取り除くことが重要となります。

CLTRの評価指標

LTRのモデルで最大化したい指標は下記式の値です。

\Delta(f_\theta,D,y) = \sum_{d_i \in D} \lambda(rank(d_i | f_\theta, D))y(d_i)

ここで、$f_\theta$はモデル、$D$は観測したアイテムの集合、$y(d_i) \in \{0, 1\}$はアイテム$d_i$がユーザにとって興味のあるかどうかを示しています。
また、$\lambda$はランキングの重み関数を表しており、Average Relevant Positionなら$\lambda(r) = r$、DCGなら$\lambda(r) = \frac{1}{log_2{(1+r)}}$、Precision@kなら$\lambda(r)=\frac{1[r \leq k]}{k}$となります。

ただし、CLTRでは$y(d_i) \in \{0, 1\}$（ユーザにとって興味のあるアイテムかどうか）は取得することができないので、実際には下記の式を最大化することになります。

\Delta(f_\theta,D,y) = \sum_{d_i \in D} \lambda(rank(d_i | f_\theta, D))c_i

ただし、$c_i \in \{0, 1}\$はアイテムがクリックされたかどうかを表している。

しかし、前章で述べたように、ImplicitなクリックデータはPosition Biasの影響を受けるため（上位に表示されたアイテムの方がクリックされやすい）、この指標を最大化するようにモデルを学習すると学習データ内で上位に表示されていたアイテムを上位に表示するようなモデルができてしまいます。

そこでCLTRでは、下記指標を最大化するようにモデルの学習を行います。

\Delta_{IPS}(f_\theta,D,y) = \sum_{d_i \in D} \frac{\lambda(rank(d_i | f_\theta, D))}{P(o_i=1|R, d_i)}c_i

ここで、$P(o_i=1|R, d_i)$はアイテム$d_i$が表示された時に閲覧される確率を表しています。

一般的には、$i$が大きくなるほど、$P(o_i=1|R, d_i)$の値が小さくなります（表示順が下にくるほど、閲覧される確率が小さくなる）。

なので、$\Delta_{IPS}(f_\theta,D,y)$は、表示順が上のアイテムがクリックされた場合より、表示順が下のアイテムがクリックされた時の方が値として大きくなります。

これにより、なるべく表示順の影響を受けないようにモデルの学習を行うのが、CLTRの考え方になります。

CLTRの手法

CLTRではPosition Biasをどのように推定するかがポイントとなります。

Unbiased Learning-to-Rank with Biased Feedback (T. Joachims el al., WSDM, 2017)ではRandPairを用いて（ランダムで表示した並び順のクリックログを集計することで、Position Biasの推定を行う）、Position Biasの推定を行なっていましたが、ランダムの並び順をユーザに提示することは、ユーザエクスペリエンスを阻害する可能性があります。

そこで、ランダムの並び順をユーザに提示せずに、EM algorithmでPosition Biasを推定するRegression-based EMという手法（Position Bias Estimation for Unbiased Learning to Rank in Personal Search)や、relevanceモデルとposition biasを推定するモデルの2つを同時に学習するDual Learning Algorithm（Unbiased Learning to Rank with Unbiased Propensity Estimation）といった手法が存在します。

これらの詳細についてはこちらの記事にまとまっています。

Online Learning to Rank (OLTR)

Counterfactual Learning to Rank (CLTR)と同様にバイアスを受けずに並び順の学習をできるロジックにOnline Learning to Rank (OLTR)というものがあります。

OLTRでは、implicit feedbackのログデータを用いてあらかじめモデルを作成するのではなく、オンラインでモデルの更新を行なっています。

本章ではまず、OLTRで使用されるInterleavingという手法について説明したのちに、OLTRのベースとなるDueling Bandit Gradient Descentについて説明します。

Interleaving

Interleavingについては、こちらの記事にわかりやすくまとまっています。

Interleavingは検索並び順やレコメンドの結果をABテストするための手法です。
普通にABテストするよりも収束が早いと言われています。

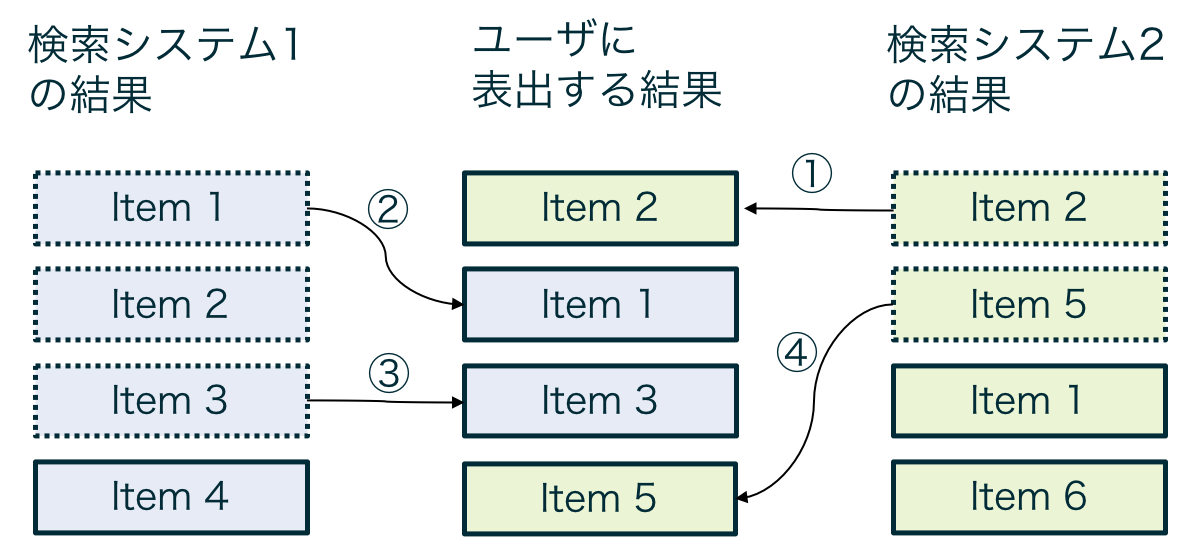
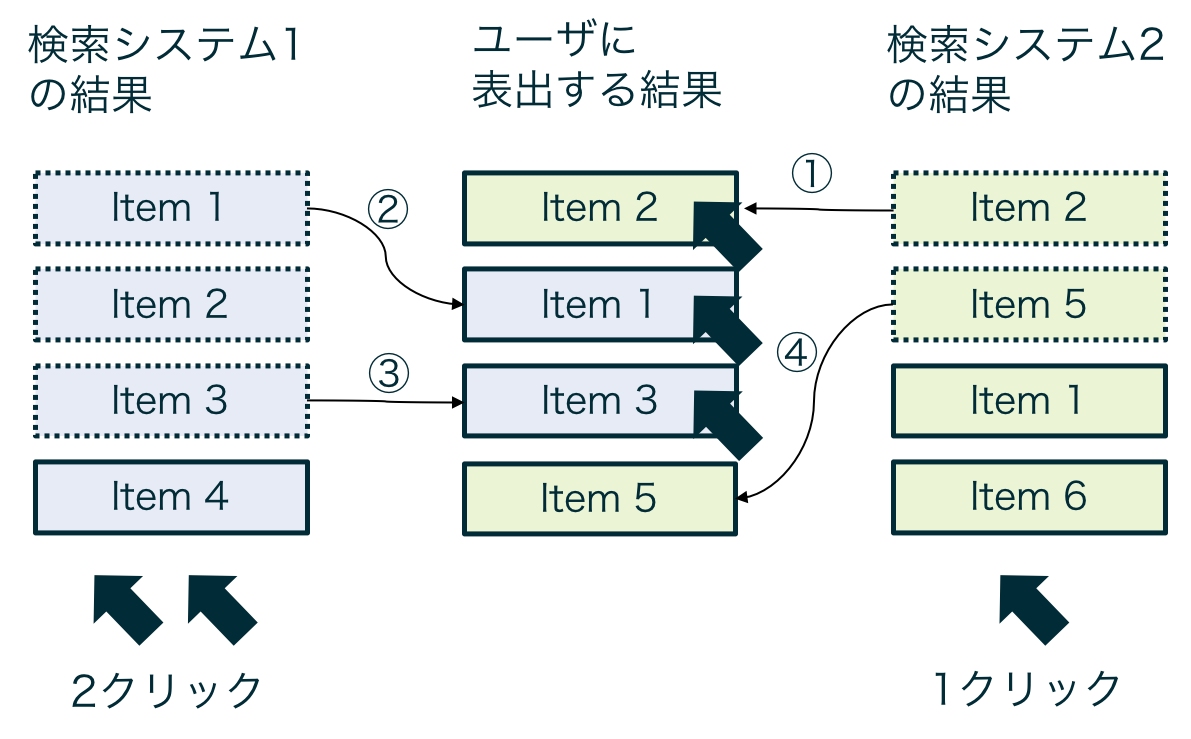
Interleavingにも色々手法は存在しますが、簡単にいうと、2つの検索（もしくは推薦）システムによって作成された結果を混ぜてユーザに提示し、どちらのシステムによって推薦されたアイテムの方がユーザにクリックされやすいか集計することで、システムの優劣の判定を行います。

図にすると以下のようなイメージになります。

クリック前	クリック後

ロジック概要

Dueling Bandit Gradient Descentについて説明します。

DBGDのpsuedo codeは以下のようになっています。

DBGDのpsuedo code

また処理フローは下記のようになります。

DBGDの処理フロー

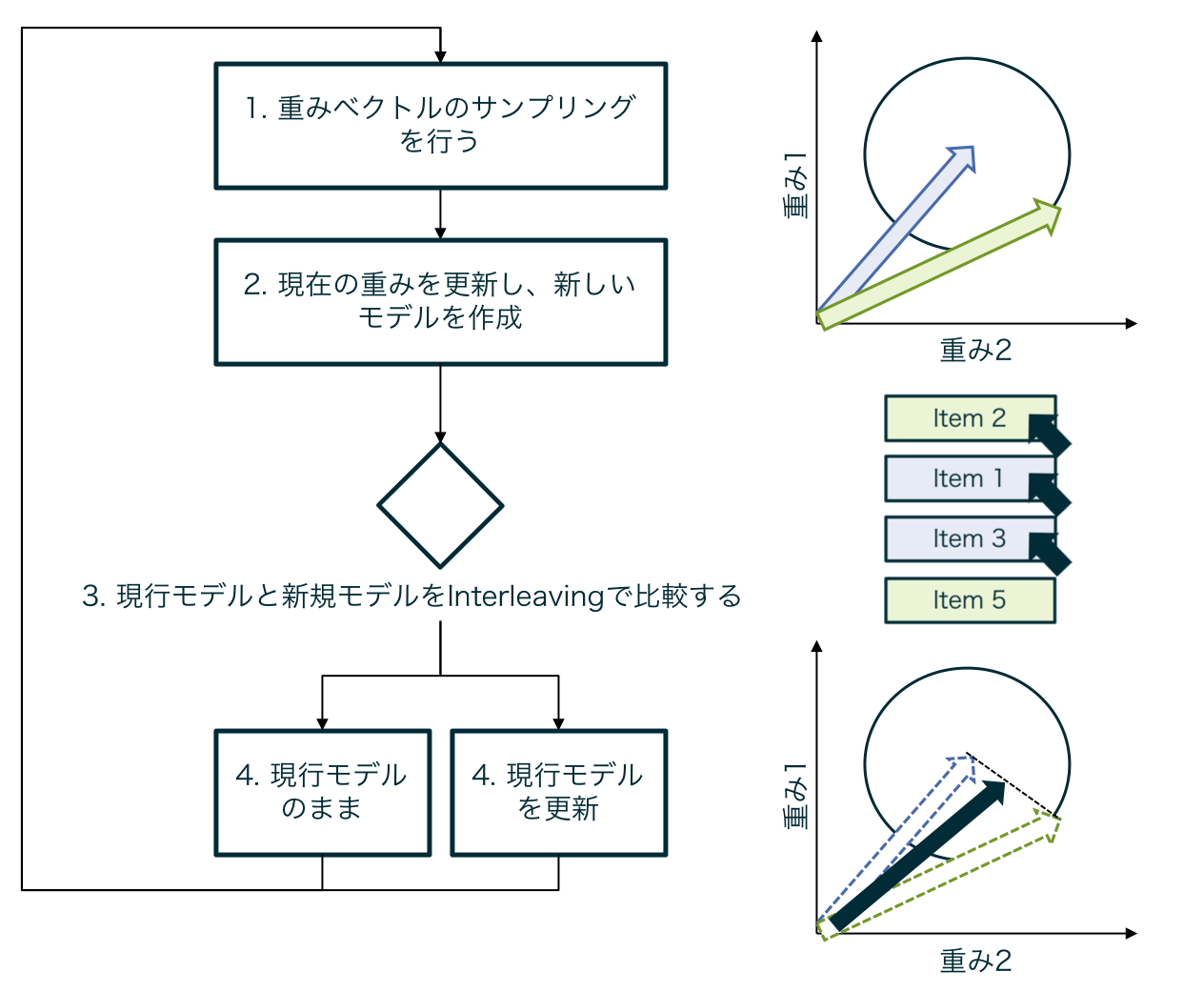DBGDではランキングモデルのパラメータを$w_t$と仮定した場合、このパラメータをランダムサンプリングによって変更することで、新規ランキングモデルを作成します（$w_t' = w_t + \delta u_t$, ただし$|\delta u_t| = C$。$C$は固定値）。

次に作成した新規ランキングモデル $w_t'$と現行ランキングモデル$w_t$をinterleavingによって比較し、モデルの優劣をつけます。

新規ランキングモデルの方が優れていた場合は、モデルのパラメータを更新し（$w_t \leftarrow　w_t + \gamma u_t$ ）、現行モデルの方が優れていた場合はパラメータの更新しません（$w_t \leftarrow w_t$）。

これをクエリごとに繰り返すことで、モデルのアップデートを行なっていきます。

DBGDではinterleavingによってパラメータの優劣をリアルタイムに行うため、バイアスを受けずにモデルの更新をすることが可能です。

以降では、OLTRのその他の手法について説明します。

Multileave Gradient Descent (MGD)

Multileave Gradient Descent（MGD）はDBGDの発展系で、interleavingではなく、multileavingによってランキングモデルの比較を行います。

multileavingとは、interleavingの拡張で、一度に3つ以上のモデルの比較を行うことができます。

multileavingのイメージ図

複数のモデルを一度に比較することができるので、DBGDと比較して、収束が早い一方で、オンラインでの計算量は大きくなってしまいます。

Document Space Projected Dueling Bandit Gradient Descent (DBGD-DSP)

Document Space Projected Dueling Bandit Gradient Descent (DBGD-DSP)のロジックについて説明します。

DBGDやMGDはランダムサンプリングによってモデルのパラメータの更新を行うので、バイアスを受けないというメリットがある一方で、モデルのバリアンス（複雑さ）が大きくなり、収束までに時間がかかるという欠点が存在します。

そこでDBGD-DSPでは、ランダムサンプルによってモデルのパラメータの更新を行い、interleavingによって新規のモデルが勝った場合は、更新に必要な重みのみを抽出して、パラメータの更新を行います。これにより、モデルのバリアンスを低下させ、収束を早くすることができます。

Psuedo codeは以下です。

DBGD-DSPのpsuedo code

DBGD-DSPでは、モデルのパラメータをランダムサンプリングによって更新する（$w_t' = w_t + \delta u_t$）、現行ランキングモデルと新規ランキングモデルをinterleavingを比較する、という部分はDBGDと同じなのですが、新規ランキングモデルが勝った際のパラメータ更新方法がDBGDと異なります。

DBGD-DSPでは、$u_t$より、全ての$i$で下記式が成り立つように$g_t$を求めます。

(w_t + \delta u_t)^T x_i = (w_t + \delta g_t)^T x_i

ただし、$x_i$はinterleavingを行なった際に用いたItemの特徴量ベクトルを表す。

下記に$g_t$を求める際のイメージ図を示す。

DBGD-DSPのイメージ図

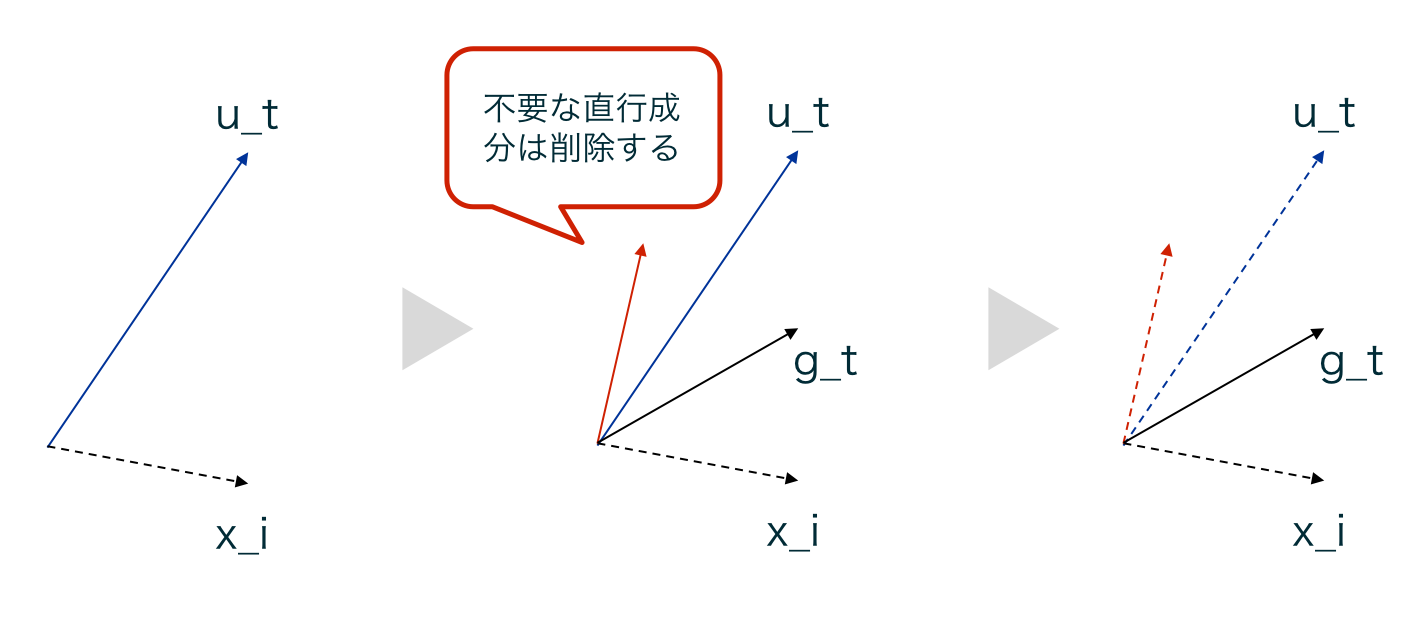$u_t$は、$x_i$に直交するベクトル成分、それ以外のベクトル成分$g_t$の2つに分解することができます。x_iに直交するベクトル成分は、x_iを用いた時のランキングモデルには影響を与えません。

そこで、$u_t$から直交ベクトル成分をのぞいた$g_t$のみを用いてパラメータの更新を行います（$w_t \leftarrow w_t + \alpha g_t$）。

これにより、バリアンスを減らすことができ、収束が早くなります。

またランダムサンプリングによってモデルのパラメータを更新するという部分はDBGDと変わらないので、バイアスを受けないという部分に代わりはありません。

Pairwise Differentiable Gradient Descent (PDGD)

DBGDやMGDといった手法は、モデルのパラメータ空間が連続的であり、また一つの最適解しか持たないという制約の元、regretの保証がされています。強い制約のため、オフラインでのロジックと比較して、精度が低くなってしまうという課題が存在しました。

そこで、DBGDとはまた別の仮定の元、オンラインでランキングモデルの学習を行う、Pairwise Differentiable Gradient Descent (PDGD)という手法が提案されました。

PDGDのpsuedo codeは下記です。

PDGDのpsuedo code

ランキングモデル$f_{\theta}(d)$によって計算されるアイテムがユーザに好まれる確率を下記のように定義します。

P(d|D, \theta) = \frac{e^{f_{\theta}(d)}}{\sum_{d'\in D} e^{f_{\theta}(d')}}　\tag{1}

ここで$d$はアイテム、$D$はアイテムの集合を表している。

PDGDでは式(1)を用いて、下記確率を最大化するようにモデルの学習を行います。

P(R|D) = \prod_{i=1}^{k}P(R_i|D \backslash \{R_i, \cdots, R_{i-1} \})　\tag{2}

$R$は生成されたランキング、$R_i$は$i$番目に表示するアイテムを表している。

この指標はPlackett-Luce modelと呼ばれ、ListNetで用いられている指標と同じです。

式(1)を用いて、アイテム$d_k$がアイテム$d_l$よりも好まれる確率を下記のように定義できます。

P(d_k \succ d_l) = \frac{P(d_k|D)}{P(d_k|D)+P(d_l|D)} = \frac{e^{f(d_k)}}{e^{f(d_k)}+e^{f(d_l)}} \tag{3}

PDGDでは式(3)を用いて、ランキングモデル$f_{\theta}(\cdot)$のパラメータ更新を行います。

\nabla f_{\theta}(\cdot) \approx \sum_{d_k >_c d_l} \rho (d_k, d_l, R, D) [\nabla P(d_k \succ d_l)] = \sum_{d_k >_c d_l} \rho (d_k, d_l, R, D) \frac{e^{f_{\theta}(d_k)}e^{f_{\theta}(d_l)}}{(e^{f_{\theta}(d_k)}+e^{f_{\theta}(d_l)})^2}(f_{\theta}'(d_k) - f_{\theta}'(d_l)) \tag{4}

ただし、$\rho (d_k, d_l, R, D)$は下記の式で求めます。

\rho(d_k, d_l, R, D) = \frac{P(R^{*}(d_k, d_l, R)|D)}{P(R|D) + P(R^{*}(d_k, d_l, R)|D)} \tag{5}

式(4), 式(5)のところを具体例で表したのが、下記図になります。

勾配計算の具体例

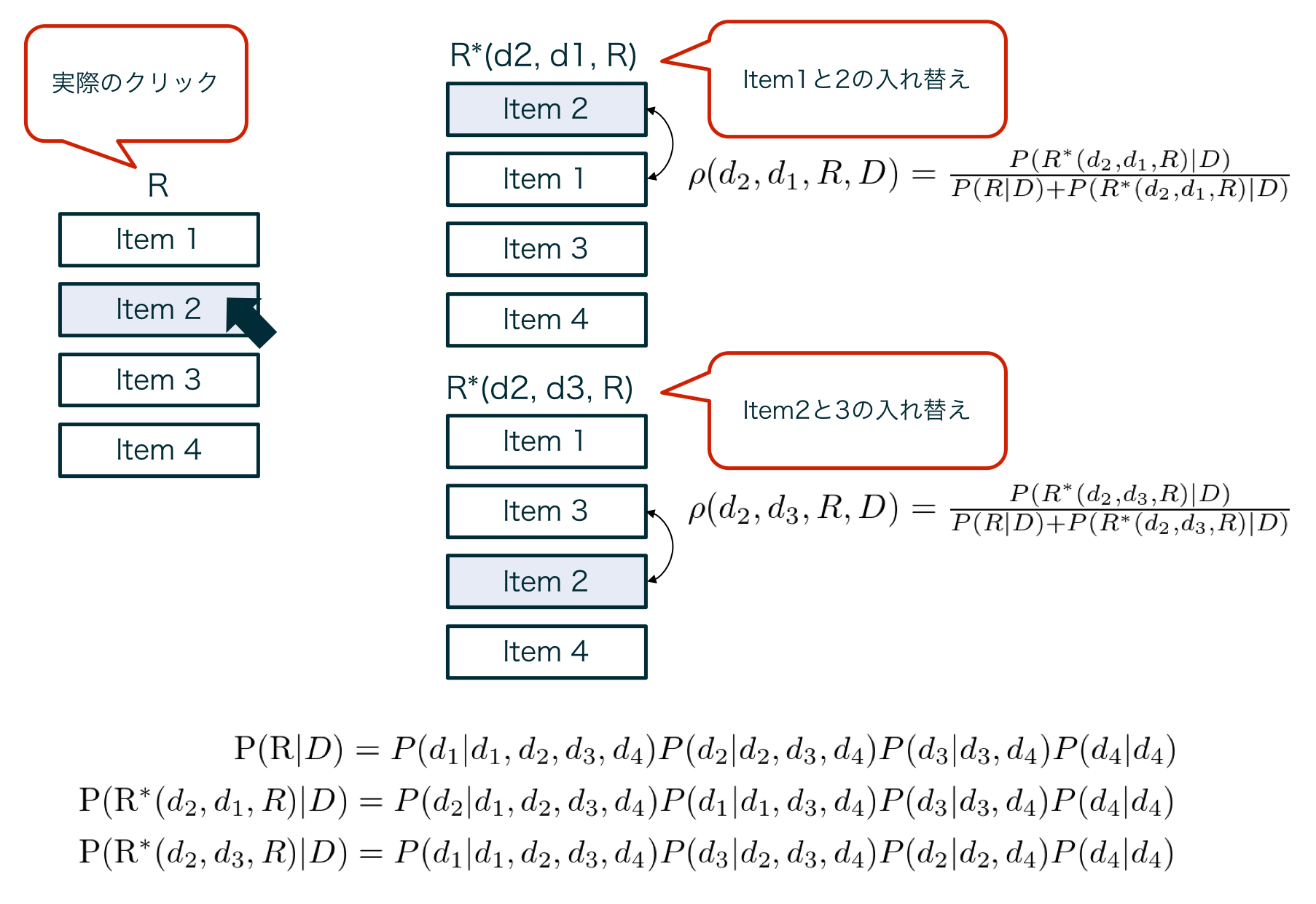PDGDで勾配を計算する際は、クリックされたアイテムが表示された箇所＋1にあるアイテムのペアを学習に使用します。
仮にItem1~4の順で表示されており、Item2がクリックされた場合、(Item1, Item2), (Item2, Item3)の2つの組み合わせを考えます。

この場合、$\rho(d_2, d_1, R, D)$は、仮にItem1とItem2の並び順が反対だった場合のPlackett-Luce modelである$P(R^*(d_2, d_1, R)|D)$を用いて、式(5)のように計算されます。

Item2, Item3の組み合わせの場合も、同様に式(5)を用いて$\rho(d_2, d_3, R, D)$を計算します。

式(5)を用いて計算した$\rho(d_2, d_1, R, D)$、$\rho(d_2, d_3, R, D)$を使って、式(4)を計算することで$\nabla f_{\theta}(\cdot)$の計算を行い、パラメータ$\theta$の更新を行います。

PDGDでは、DBGDのような制約（モデルのパラメータ空間が連続的であり、また一つの最適解しか持たない）をおかずにパラメータの更新ができるので、表現力の高い複雑なモデルにも適用することができます。

またポジションバイアスの影響を受けないことも論文内で証明されており、オフラインの実験でDBGDより精度が高くなることが示されています。

Counterfactual vs Online

本章では、Counterfactual Learning to Rank (CLTR)とOnline Learning to Rank (OLTR)の精度比較を行なった論文について紹介させていただきます。

SIGIR2019で発表されたTo Model or to Intervene: A Comparison of Counterfactual and Online Learning to Rank from User Interactionsという論文です。

ロジック

該当論文では、CLTRのロジックとして、Unbiased Learning-to-Rank with Biased Feedback (T. Joachims el al., WSDM, 2017)のロジックを、OLTRのロジックとして、Pairwise Differentiable Gradient Descent (PDGD)を用いて、シミュレーションベースで精度の比較を行いました。

データセット

データにはYahooデータセットを用いています。

Yahooデータセットは記事の関連度として、0~4のラベルが振られている。論文内では、この関連度を用いて記事がクリックされる確率$P(click=1|observed=1,rel(d)$のモデリングを下記のように3パターン行います。

記事がクリックされる確率のモデリング

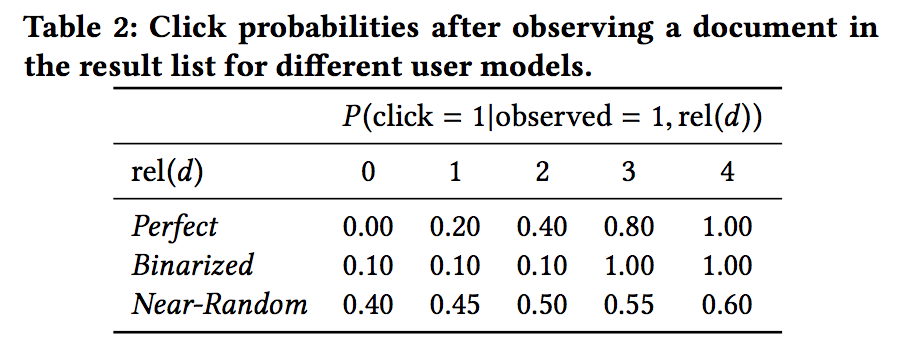また、$i$番目の記事が閲覧される確率$P(observed=1|i)$は下記の式を元にモデリングしています。

P(observed=1|i) = (\frac{1}{i})^{\eta}

実験では$\eta = 1$, $\eta=2$の2パターンを用いていました。

またselectionバイアス（上位N件だけのアイテムが表示される）を考慮するために、selectionバイアスがある場合（N=10）とない場合のそれぞれの条件で実験を行なっていました。

結果

$\eta=1$	$\eta=2$

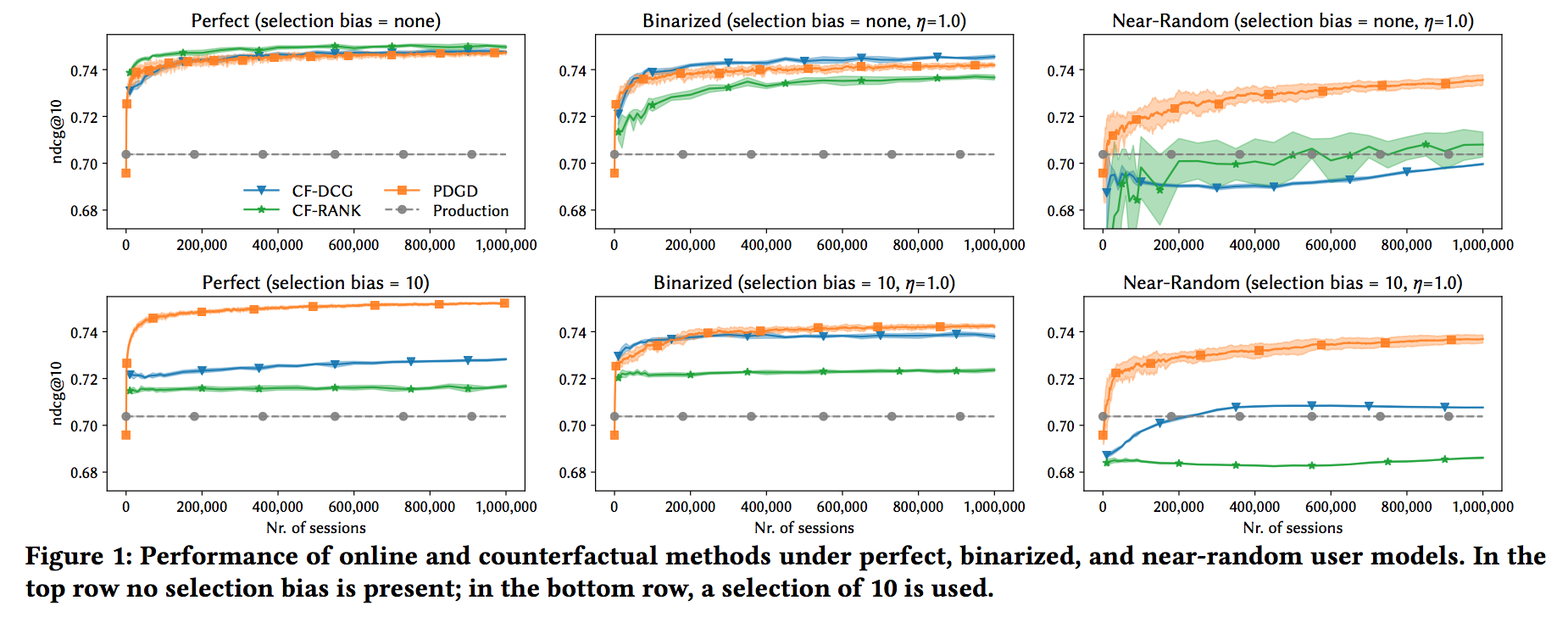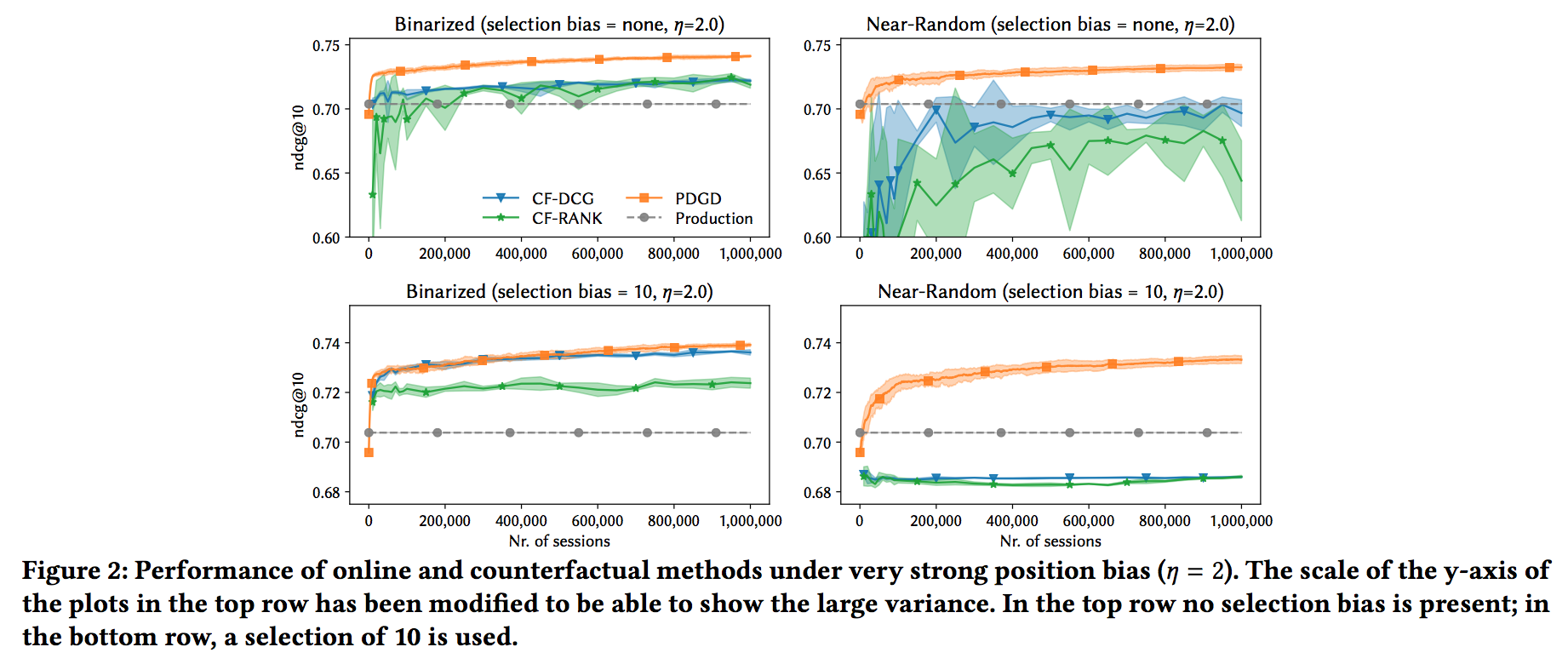上の図では、selection bias = {none, 10}、クリックされる確率 = {Perfect, Binarized, Near-Random}でイテレーションごとのnDCG@10の値をCLTRとOLTRで比較しています。

selection biasがなく、クリックされる確率がPerfect（relevanceによってクリック確率が上がる）場合は、CLTRの方が精度が高いが、selection biasがある場合や、クリックされる確率がランダムに近い場合（ノイズが大きい）は、OLTRの精度の方が高い結果がでた、というのがこの論文での主張でした。

まとめ

本記事では、Learning to Rank with Implicit Feedbackという概念の説明を行い、2つの手法であるCounterfactual Learning to Rank (CLTR)、Online Learning to Rank (OLTR)に関して、具体例を踏まえて説明を行ないました。
最後に、CLTRとOLTRの精度比較をオフラインで行なった論文に関して簡単に説明をしました。

個人的にはPDGDをオンラインで試してみたいです。