遺伝的アルゴリズムなるものをやってみました。ほんとは夏休みはいったらサポートベクターマシン実装するぞって思ってたんですけど使われてる理論がちょっと難しかったので熟成させます。今回はよくあるランダムに生成された01のベクトルを1になるようにするというやつをやりました。これ、僕は最初は「いやいや全部1にするなんて自明じゃんか」って思ってたんですけど、よく考えたら2^n通りのパターンがあって全探索するとNP問題と同様の計算量が必要なのだということを今日の夕ご飯を食べてるときにふと思いました。(夕ご飯はカレーでした)そんなこんなで書いていきたいと思います。
遺伝的アルゴリズムとは
僕も授業でちょっとだけ聞いたのと、その辺のサイトを読んでいただけなので詳しくはわからないんですが、名前の通り、生物の適者生存の仕組みを最適化問題に取り入れたメタヒューリスティクスです。
①遺伝子を生成する
②適している遺伝子を選択する
③生き残った遺伝子を交配して子孫を生み出す。
④低い確率で突然変異を起こす。
⑤既定の精度もしくは決められた回数に満たなければ②に戻る
ということをくり返していくものです。何となく想像がつきますよね。僕も交配してえ
遺伝子を生成する
今回は遺伝子はランダムに0か1かをそれぞれ乱数を使って決めて生成しました。
適している遺伝子を選択する
遺伝子の選択方法にはいろんな種類があるのですが、今回はルーレット選択なるものを用いました。ルーレット選択は下の画像のように適合度が大きいほど選ばれる確率を高くしてやる方法です。選ぶときにはこの円グラフの適当な点をランダムに選択してそこに該当する遺伝子を選ぶみたいな感じにします。その操作をそれぞれ独立に親の遺伝子と同じ数の遺伝子がそろうまでやります。
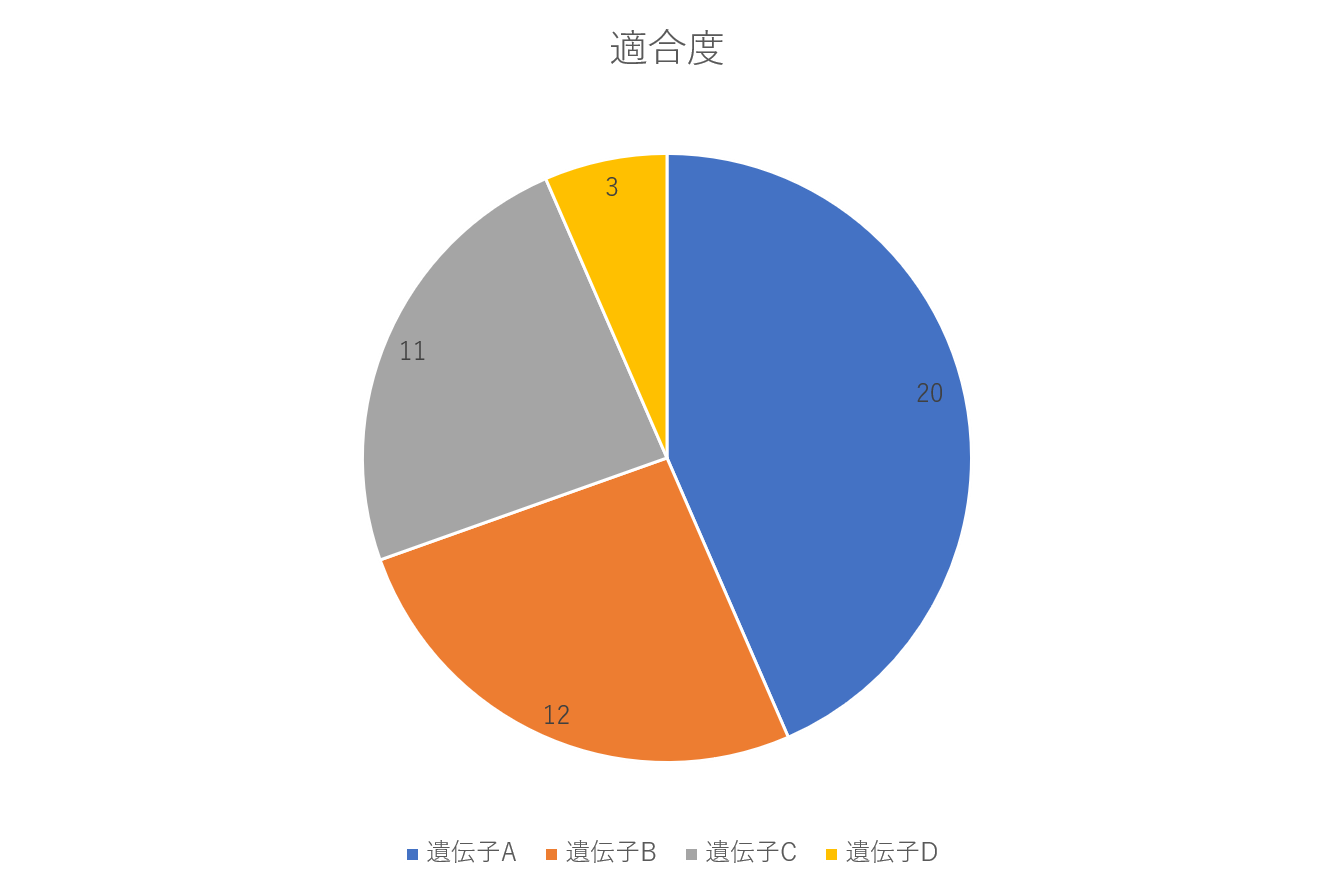
今回は、このほかにエリート選択というものを使いました。ランダムで遺伝子が選ばれるので最悪、悪い遺伝子ばかり選ばれる場合があります。これを避けるために強制的に一番いい遺伝子を子孫繁栄に使ってやろうというものです。
遺伝子を交配する
遺伝子を交配するのに該当する操作を交叉と呼びます。これにもいろんな方法があって今回は二点交叉というものを用います。これはどういったものかというと、ランダムに二点を選択してその二点間の遺伝子を交換するという方法です。

このような二つの遺伝子を二つの点を決めてやって入れ替えます。すると下のようになります。
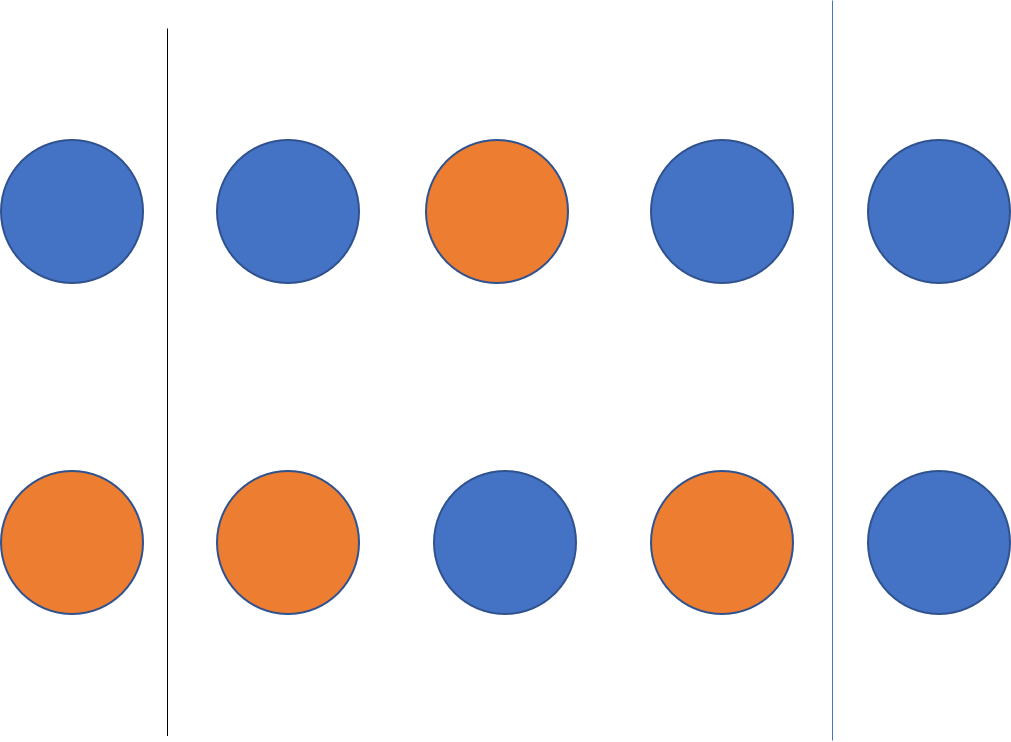
手順としては、交配させるペアを何組か生成し、高い確率で交配させます。今回は80%で行いました。
遺伝子を突然変異させる
放射線なんかの影響で遺伝子が切断されたような場合に該当します。発生確率は0.1%から数%と非常に低い確率にします。これを高くしすぎてしまうとランダム探索になってしまうので気を付けてください。これもいろんな種類があるんですけど、一般的には発生する個体の遺伝子のある一点を0から1、または1から0に変えます。(今回の場合はこれを使用しました。)
ここから実装
まずはいろいろ初期化します。
package main
import (
"math/rand"
"fmt"
)
/*
遺伝的アルゴリズムを実装していみる
ルーレット選択、二点交叉を用いる
エリート保存も行う
*/
//遺伝子の長さ
var genom_length = 100
//遺伝子の数
var genom_size = 100
//交叉するペアの数
var cross_pairs = 30
//交叉する確率 小数点第二位まで
var cross_prob = 0.8
//繰り返す世代数
var generation = 500
//突然変異確率 小数点第三位まで指定しておk
var mutation_prob = 0.01
//遺伝子配列
var ls = [][]int{}
//遺伝子の配列を作ります(初期値)
func init() {
ls = make([][]int,genom_size)
for i:=0;i<genom_size;i++{
ls[i] = make([]int,genom_length)
for j:=0;j<genom_length;j++{
ls[i][j] = rand.Intn(2)
}
}
}
このあと必要そうになってくる関数を実装します。二分探索はルーレット選択の取り出すやつを高速化するために実装してます。
//遺伝子の優秀さを評価する
func accuracy(ls []int) int {
c := 0
for i:=0;i<len(ls);i++{
if ls[i] == 1{c ++}
}
return c
}
//スライスを二分探索して指定した数が入りそうなインデックスを返す
//スライス[2,5,7,9,10] n = 6のとき2を返す
func binary_search(list []int,n int) int {
if list[0] >= n {
return 0
}
front := 0
back := len(list) - 1
for {
i := (front + back) / 2
if list[i] >= n{
back = i
} else {
front = i
}
if back - front == 1{
return back
}
}
}
ルーレット選択を実装します。ルーレット選択は、遺伝子の優秀さの累積和を取ってあげます。その後、0~最大の数の範囲で乱数で数字を生成し、二分探索で該当しそうなインデックス番号を探すという実装になっています。
//ルーレット選択を行います。
func selectGenetic() [][]int {
//次の世代
next_generation := make([][]int,genom_size)
//ルーレット選択用の重みを格納したスライス
select_list := make([]int,genom_size)
for i:=0;i<genom_size;i++{
select_list[i] = accuracy(ls[i])
if i != 0{select_list[i] += select_list[i-1]}
}
//エリート選択を実装 一番よい個体を強制的に後世に残す
maxIndex := 0
maxAccuracy := 0
for i:=0;i<len(ls);i++{
cc := accuracy(ls[i])
if maxAccuracy < cc{
maxIndex = i
maxAccuracy = cc
}
}
next_generation[0] = make([]int,genom_length)
//怖いからコピー走らせとく
for j:=0;j<genom_length;j++{
next_generation[0][j] = ls[maxIndex][j]
}
//指定回数分だけランダムに取り出す
for i:=1;i<genom_size;i++{
next_generation[i] = make([]int,genom_length)
n := rand.Intn(select_list[len(select_list)-1]+1)
index := binary_search(select_list,n)
//怖いからコピー走らせとく
for j:=0;j<genom_length;j++{
next_generation[i][j] = ls[index][j]
}
}
//置き換え
ls = next_generation
return next_generation
}
二点交叉を実装します。長くなってしまったので二つのインデックスの組を生成するmakePairs関数と実際に交叉を行うcrossing関数を実装しました。
//cross_pars個のペアを生成する関数 インデックスを返す
//ようは重複を許さずに乱数でわちゃわちゃするということ
func makePairs() [][]int {
check_ls := make([]int,genom_size)
for i:=0;i<len(check_ls);i++{
check_ls[i] = i
}
//おなじみのフィッシャーなんたらのアルゴリズムでシャッフル
for i:=len(check_ls)-1;i>0;i--{
n := rand.Intn(i)
check_ls[i],check_ls[n] = check_ls[n],check_ls[i]
}
//頭から二つずつ入れてく
ans := make([][]int,cross_pairs)
for i:=0;i<cross_pairs*2;i++{
if i%2 == 0{ans[i/2] = make([]int,2)}
ans[i/2][i%2] = check_ls[i]
}
return ans
}
//二点交叉する関数。
//引数に渡した配列をそのまま変える
func crossing() {
indexes := makePairs()
for i:=0;i<len(indexes);i++{
prob := rand.Intn(100)
if int(cross_prob*100) - 1 < prob{continue}
a := rand.Intn(genom_length)
b := rand.Intn(genom_length)
if a > b{a,b = b,a}
for j:=a;j<b;j++{
ls[indexes[i][0]][j],ls[indexes[i][1]][j] = ls[indexes[i][1]][j],ls[indexes[i][0]][j]
}
}
}
突然変異を起こす関数を実装します。上の説明そのままです。
//突然変異を起こす
func mutation() {
for i:=0;i<len(ls);i++{
n := rand.Intn(1000)
if int(mutation_prob*1000) - 1 < n{continue}
n = rand.Intn(genom_length)
if ls[i][n] == 0{
ls[i][n] = 1
} else {
ls[i][n] = 0
}
}
}
最後にメイン関数で今回の処理をまとめます。
func main(){
//世代数だけループ
for i:=0;i<generation;i++{
selectGenetic()
crossing()
mutation()
}
//一番良い個体を出力
maxIndex := 0
maxAccuracy := 0
for i:=0;i<len(ls);i++{
if maxAccuracy < accuracy(ls[i]){
maxIndex = i
maxAccuracy = accuracy(ls[i])
}
}
fmt.Println(ls[maxIndex])
fmt.Println(maxAccuracy)
fmt.Print("のん!")
}
500世代時を重ねた結果
出力
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
97
のん!
さいごに
最後まできてあれなんですけど、実は量子アニーリングに興味があって先生に頼んで自主ゼミでちょっとだけ「量子アニーリングの基礎」という本をこの春学期勉強しました。なのでメタヒューリスティクスでは遺伝的アルゴリズムよりも仕組みが似てそうなシミュレーテッドアニーリングの方が興味あります。
追記
評価関数を連続する二つの積の和とした場合の方が少し良い性能が出ました。これはできるだけ1が連続したほうが良いという評価にしたことで優秀な遺伝子に挟まれて生き残り続ける優秀でない遺伝子を早い段階で排除できたからだと思われます。つまり、11111011011111のよう
な遺伝子が淘汰されやすくなったと考えられます。
//遺伝子の優秀さを評価する
func accuracy(ls []int) int {
c := 0
for i:=1;i<len(ls);i++{
//if ls[i] == 1{c ++}
c += ls[i-1]*ls[i]
}
return c
}