目的
統計モデリングについて勉強を進めるために基礎的な知識を身につける。
まずはポワソン分布から。
参考にしたもの
ノート
いろいろと試した結果を以下に置いた。
以下、学習結果を一部抜粋
ポアソン分布の利用方法
- プロシア陸軍において馬に蹴られて死んだ兵士数
- 交通事故件数
- 大量生産の不良品数
- 破産件数
- 火災件数
- 砲弾命中数
- 遺伝子の突然変異数
- 電話の呼び数
- 渋滞していない高速道路の料金ゲートへの車の到着数
(東京大学出版会 統計学入門より)
λのみにより分布が求められる。
λは与えられたデータセットの平均をセットする。
この性質により、データセットの平均値のみからレアケースの確率分布が取得できるというメリットがある。
例題
以下の例題を考えてみた。
年間50件交通事故が発生している市で、1日あたり交通事故が2件以上発生する確率
以下抜粋
from scipy.stats import poisson
accident_per_day = 50 / 365
poisson_arr = np.random.poisson(lam=accident_per_day, size=10000)
max_val = np.max(poisson_arr)
# ポワソン分布に従った確率変数を取得
x_range = np.arange(max_val + 1)
poisson_prob = poisson.pmf(x_range, mu=accident_per_day)
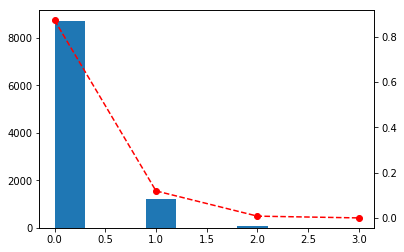
fig, ax1 = plt.subplots()
ax1.hist(x=poisson_arr, align='mid', bins=10)
ax2 = ax1.twinx()
ax2.plot(x_range, poisson_prob, 'ro--')
plt.show()
2軸になったことでy軸の原点がずれているが、おおむね傾向は問題なさそう。
2件/1日以上となるところを抽出すると以下の通りとなる。
# ランダムで発生したpoisson分布から求めた2件/1日以上の交通事故が発生する可能性
arr_over_2 = np.sum(poisson_arr > 1) / 10000
print('1日2件以上の交通事故発生確率: {}'.format(arr_over_2))
# poisson分布に従った確率分布から求めた2件/1日以上の交通事故が発生する可能性
prob_over_2 = np.sum(poisson_prob[2:])
print('1日2件以上の交通事故発生確率: {}'.format(prob_over_2))
1日2件以上の交通事故発生確率: 0.0086
1日2件以上の交通事故発生確率: 0.008555063881597425
どちらのパターンでも同じような確率になっていることが分かった。