互いに素な数をつないだ整数ネットワーク

はじめに

ノードを整数、リンクを互いに素な組、としてネットワークをかいたら面白いことになるんじゃないか！と、ふと思ってやってみました。
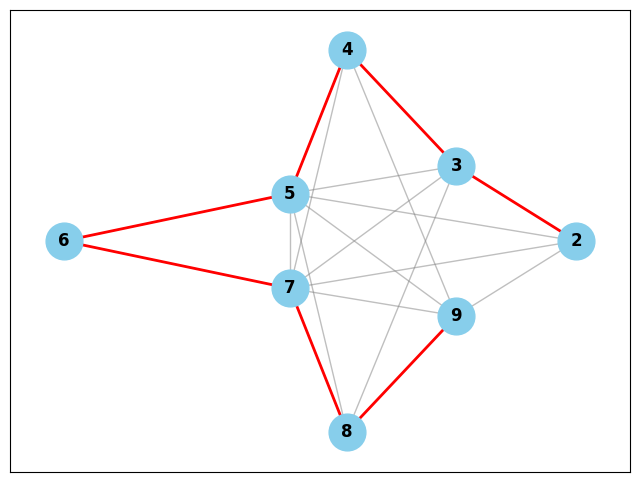
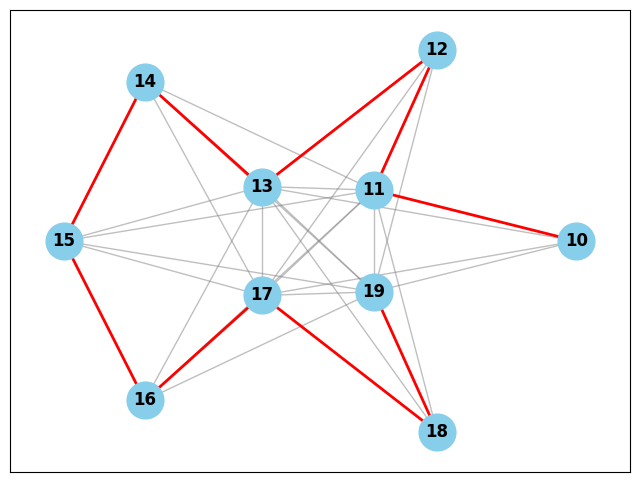
差が1の数の組は互いに素なので、ネットワークは必ず連結になります。せっかくなので差が1のリンクは目立たせてみました。タンパク質のフォールディングみたいに鎖がどんな形になるのか見てたら楽しそう。

互いに素な整数ネットワーク

以下のコードでネットワークを描画できます。pythonでかきました。

コード

import networkx as nx
import matplotlib.pyplot as plt
import math

# 互いに素かどうかを判定する関数
def are_coprime(a, b):
    return math.gcd(a, b) == 1

# ノードの範囲（例2〜9の整数）
nodes = range(2, 10)

# グラフの作成
G = nx.Graph()

# ノードをグラフに追加
G.add_nodes_from(nodes)

# ノード間にエッジを追加（互いに素なペア）
edges = []
highlight_edges = []  # 連続する数のエッジを保存するリスト
for i in nodes:
    for j in nodes:
        if i < j:
            if are_coprime(i, j):
                edges.append((i, j))
            # 連続する数を特定
            if j == i + 1:
                highlight_edges.append((i, j))

# グラフにエッジを追加
G.add_edges_from(edges)

# 配置方法の指定
pos_grid = nx.kamada_kawai_layout(G)
plt.figure(figsize=(8, 6))

# 通常のエッジを描画
nx.draw_networkx_edges(G, pos=pos_grid, edgelist=edges, edge_color='gray', alpha=0.5)

# 連続する数のエッジを目立たせる（太さと色を変更）
nx.draw_networkx_edges(G, pos=pos_grid, edgelist=highlight_edges, edge_color='red', width=2)

# ノードを描画
nx.draw_networkx_nodes(G, pos=pos_grid, node_size=700, node_color='skyblue')

# ラベルを描画
nx.draw_networkx_labels(G, pos=pos_grid, font_size=12, font_weight='bold')

# 出力
plt.show()

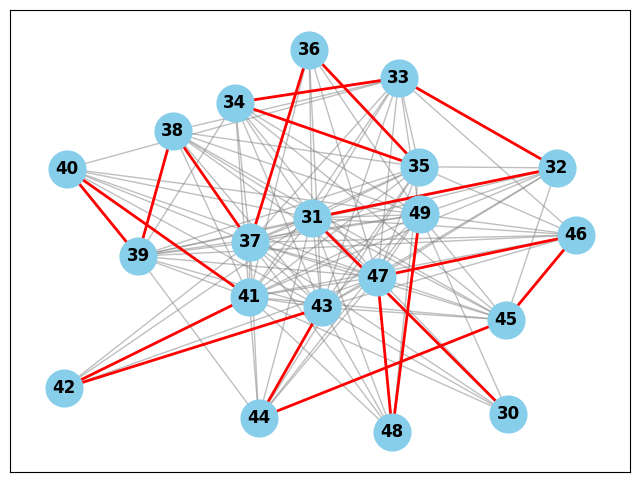
実際のネットワークは以下です。

ノード：２～９

ノード：10～19

ノード：20～29

ノード：30～49

ノード：2～49

おわりに

うーん。なんだかよくわからないですね！私が気づいてないだけで、面白い性質はたくさんあるのかしら？
ノード2~49の図でいくつかのかたまりができていますが、何か意味があるんだろうか...？。中央には大きめな素数が固まっています。
素数がリンクを持ちやすいので、素数を外してみても面白いのかも。あと、逆に共通因数を持つものにリンクをはるとか。ノードのポジションの決め方もいろいろかえてみるとまた発見があるかもしれません。距離とかクラスター係数とかのネットワーク特徴量を見てもいいのかしら。
もしここから何かおもしろいことをひらめいた人は好きに研究してください！では！