Mathematicaでの積分
先日は,RIKENでカンファレンスがありましたね.10月のイリノイでのWTC2015といい今回といい参加できていないのを残念がっている私です...
さて,そんな私の個人的な事情はさておき.
Mathematicaは非常に強力な計算能力にお世話になっている方もきっと多いはず.
特にカオス系では機械計算に頼らざるをえない部分がありますので,そんな時に(たぶん役立つ)tipsを描いてみます.軌道を描いたり,積分の桁精度を上げたり,止めてみたり,途中の情報を取得してみたり...です.
NDSolveで積分してみよう
Mathematicaでの積分は以下のようなNDSolveであっさり出来てしまいます.
sol = NDSolve[{eqns, ics}, vars, {t, 0, tMax}]
もちろん各所には事前に適切な値を入れておきますが,これだけで非常に精度の高いInterpolatingFunctionが得られることは驚きです.
たとえばKepler問題の変形版:AKP(anisotropic Kepler problem)の式ならば
tMax = 25;
\[Gamma] = 2/10;
\[Mu] = Sqrt[1/\[Gamma]]
\[Nu] = 1/\[Mu]
x0 = 1;
y0 = 0;
px0 = 0;
py0 = 1/5^(1/4);
eqns = {
x'[t] == px[t]/\[Mu],
y'[t] == py[t]/\[Nu],
px'[t] == -(x[t]/(x[t]^2 + y[t]^2)^((3/2))),
py'[t] == -(y[t]/(x[t]^2 + y[t]^2)^((3/2)))
};
ics = {x[0] == x0, y[0] == y0, px[0] == px0, py[0] == py0}
vars = {x[t], y[t], px[t], py[t]};
といった感じです.
この軌道を描いてみたいと思った時は
xys = Table[{x[t], y[t]} /. First[sol] /. t -> tt, {tt, 0, tMax,
10^-2}];
Graphics[Line[xys], PlotRange -> {{-2, 2}, {-2, 2}}, AspectRatio -> 1,
Axes -> True]
といった感じです.
描いてみた結果は
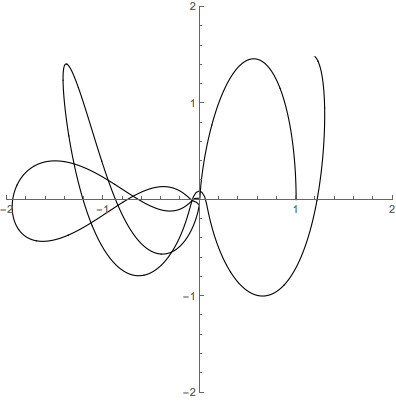
といった感じでしょう.
まぁごちゃごちゃですよねw
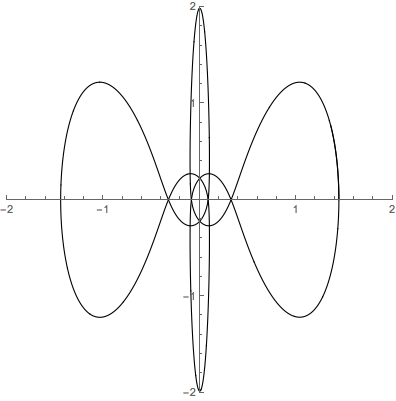
まさしくカオス!!という感じがしてこれはこれで良いと思いますが,初期条件を変えれば
といった感じの美しい周期軌道にもなります.
(実は僕の研究の1つがこれでして...もし他の周期軌道の例をご覧になりたい場合は,
rank 10 POs
AROB
をどうぞ[宣d...])
桁精度を変える
Singularityに近くて計算が大変!!うまく避ける方法で計算すれば良いけど,ちょっと力技でゴリ押ししたい!!
という時もあるでしょう.そんな時,計算の精度を倍精度以上に変えてしまうという手法があります.
桁精度を変更するには
sol2 = NDSolve[{eqns, ics}, vars, {t, 0, tMax},
WorkingPrecision -> 32, MaxSteps -> Infinity]
とするだけです.
ここでは倍精度から4倍精度(32桁)に変更してみました.
桁を増やしたぶん,計算は重くなりますが効果的です.
ただし,一つ注意すべきは,Mathematicaはデフォルトで機械精度で計算するため,初期条件としてinputするときに,整数,分数もしくは目的の桁以上の小数を代入させることが必須です.これを忘れるといくらWorkingPrecisionをあげても,機械精度で計算されてしまいます.
また,計算Methodも多く用意されており,
sol3 = NDSolve[{eqns, ics}, vars, {t, 0, tMax},
Method -> "StiffnessSwitching", WorkingPrecision -> Prec,
MaxSteps -> Infinity]
というように使用していきます.
計算を好きなところで止めたい
積分を実行していると,特定の条件で積分を止めたいということがあるでしょう.
そんなときに役に立つのが”EventLocator”です.
(__cooperさんから教えていただきましたがWhenEvent関数でも書けるようです(むしろその方が書きやすいかもです).WhenEvent関数で書いた例は下記コメント欄に記載しておりますので,気になる方は参考にしていただければ幸いです.__cooperさん,情報提供ありがとうございました.)
例えば,”y=0で止めたい”と思った時は,
sol4 = NDSolve[{eqns, ics}, vars, {t, 0, tMax},
Method -> {"EventLocator",
"Event" :> y[t],
"EventAction" :> "StopIntegration",
Method -> "StiffnessSwitching"}, WorkingPrecision -> Prec,
MaxSteps -> Infinity]
といった感じです.
計算を好きなところで止めたい & その時々の情報を取得したい
上では,単純にy=0に初めてなった時点で計算を止めてしまいましたが,計算をやっていると,”何回目で止めたい”or"途中の情報を取得したい"といった要求が出てくるでしょう.
そんな時も”EventLocator”です.
”EventLocator”の”Event”を2段階に設定することで実現できます.
こんな感じです.
solPSScut = NDSolve[{eqns, ics}, vars, {t, 0, tMax},
Method -> {"EventLocator",
"Event" :> {y[t], (icut - icutmax)},
"EventAction" :> {{icut++, {PSSData[[icut]] = {icut, t, x[t],
y[t], px[t], py[t]}}}, {"StopIntegration"}},
Method -> "StiffnessSwitching"}, WorkingPrecision -> Prec,
MaxSteps -> Infinity];
ここでは,
icutがy=0ごとに1ずつ増えて,同時にPSSDataとして予め用意していたtableに各データを収納します.そしてicutがicutmaxに達した時,初めて"StopIntegration"が効き,積分が止まるという仕組みです.
(PSSDataのPSSはポアンカレ断面(Poincare surface of section)に由来しています)
おわりに
以上,色々積分をする際に役立つと思っていることを書いてみましたが,いかがでしたしょうか?
大まかには”NDSolve”, "WorkingPrecision","EventLocator(or WhenEvent)"です.
途中個人的な宣伝も入れてしまいましたが,Mathematicaでの積分Lifeを楽しんでいただけたら幸いです.