はじめに
Gurobi Optimizerをインストールしたあとに、まずはサンプルとして簡単な数理最適化問題を解いてみたくなると思います。ここでは、Pythonインターフェースを使ったコードを紹介し、ポイントをかいつまんで解説します。
復習記事
想定環境
- Windows 10 64bit
- Gurobi Optimizer 8.0.1
- Python 3.6
主な公式ドキュメント類のありか
-
クイックスタートガイド
スタート → Gurobi 8.0.1 (win64) → Gurobi Quick Start Guide (8.0.1)
(または、C:\gurobi800\win64\docs\quickstart\quickstart.html) -
Pythonインターフェースの例
クイックスタートガイド → Python interface -
サンプルコード
C:\gurobi801\win64\docs\examples\python\
サンプル1
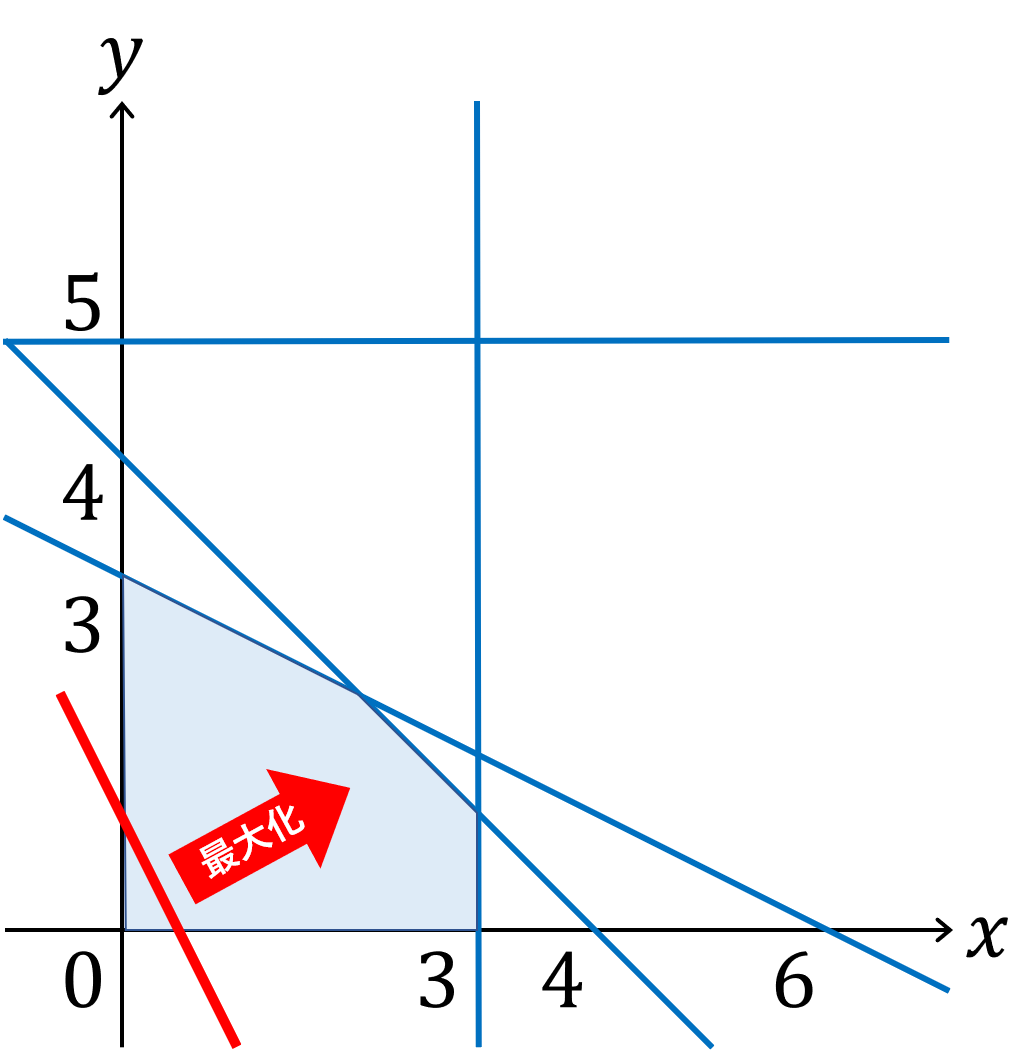
最適化問題
\begin{alignat}{2}
&\mbox{最大化}
&\qquad 2x + y & \\
&\mbox{制約}
& x + y &\leq 4 \\
&
& x + 2y &\leq 6 \\
&
& 0 \leq x &\leq 3 \\
&
& 0 \leq y &\leq 5. \\
\end{alignat}
最適化問題を図示したもの
コードと実行結果
# coding: utf-8
# Dummy Japanese character: あ(意味はないが確実に日本語を含むファイルにする)
# パッケージをインポートし、"gp"という短縮名を設定(違う短縮名にしてもよい)
import gurobipy as gp
# 問題を設定
model_1 = gp.Model(name = "GurobiSample1")
# 変数を設定(変数単体にかかる制約を含む)
x = model_1.addVar(lb = 0, ub = 3, vtype = gp.GRB.CONTINUOUS, name = "ekkusu")
y = model_1.addVar(lb = 0, ub = 5, vtype = gp.GRB.CONTINUOUS, name = "wai")
# 目的関数を設定
model_1.setObjective(2 * x + y, sense = gp.GRB.MAXIMIZE)
# 制約を設定
c_1 = model_1.addConstr(x + y <= 4, name = "seiyaku_1")
c_2 = model_1.addConstr(x + 2 * y <= 6, name = "seiyaku_2")
# 解を求める計算
print("↓点線の間に、Gurobi Optimizerからログが出力")
print("-" * 40)
model_1.optimize()
print("-" * 40)
print()
# 最適解が得られた場合、結果を出力
if model_1.Status == gp.GRB.OPTIMAL:
# 解の値
x_opt = x.X
y_opt = y.X
# 目的関数の値
val_opt = model_1.ObjVal
print(f"最適解は x = {x_opt}, y = {y_opt}")
print(f"最適値は {val_opt}")
↓点線の間に、Gurobi Optimizerからログが出力
----------------------------------------
Optimize a model with 2 rows, 2 columns and 4 nonzeros
Coefficient statistics:
Matrix range [1e+00, 2e+00]
Objective range [1e+00, 2e+00]
Bounds range [3e+00, 5e+00]
RHS range [4e+00, 6e+00]
Presolve time: 0.00s
Presolved: 2 rows, 2 columns, 4 nonzeros
Iteration Objective Primal Inf. Dual Inf. Time
0 8.0000000e+00 1.000000e+00 0.000000e+00 0s
1 7.0000000e+00 0.000000e+00 0.000000e+00 0s
Solved in 1 iterations and 0.00 seconds
Optimal objective 7.000000000e+00
----------------------------------------
最適解は x = 3.0, y = 1.0
最適値は 7.0
解説
model_1 = gp.Model(name = "GurobiSample1")
gp.Modelクラスのコンストラクターを呼び出してオブジェクトを生成し、model_1に代入しています。この時点でのmodel_1は、目的関数や制約がまだ設定されていない、空の数理最適化問題にあたります。
x = model_1.addVar(lb = 0, ub = 3, vtype = gp.GRB.CONTINUOUS, name = "ekkusu")
y = model_1.addVar(lb = 0, ub = 5, vtype = gp.GRB.CONTINUOUS, name = "wai")
数理最適化問題model_1に、2つのaddVar()メソッドにより、2つの変数を加えています。また、このメソッドは、戻り値として、生成された変数をgp.Varクラスのオブジェクトにて返すので、返された2つの変数のオブジェクトをxやyに代入しています。
addVar()メソッドの引数の意味は以下のとおりです。省略すると何らかのデフォルト値が適用されます(詳しくは、この記事の末尾の「より詳しい公式ドキュメント類のありか」で触れているPython API詳細を参照)。大抵の場合はこのサンプルのように4つの引数を設定すればよいと思います。
-
lb| 変数の下限値- マイナス無限大を設定したい場合は
- gp.GRB.INFINITYとする
- マイナス無限大を設定したい場合は
-
ub| 変数の上限値- プラス無限大を設定したい場合は
gp.GRB.INFINITYとする
- プラス無限大を設定したい場合は
数理最適化問題の制約のうち、各変数単体についての下限値・上限値は、ここで設定するのがよいです。
-
obj| 目的関数で、この変数にかけられる係数- このサンプルのように、
setObjective()メソッドで目的関数を設定する場合は、ここで係数を設定する必要はない - 列生成法などの列方向モデリングしたいときに役に立つ
- このサンプルのように、
-
vtype| 変数の種類-
gp.GRB.CONTINUOUSまたは"C"| 連続変数 -
gp.GRB.BINARYまたは"B"| 0-1変数- これを指定した場合、自動的に
lb = 0, ub = 1になる
- これを指定した場合、自動的に
-
gp.GRB.INTEGERまたは"I"| 整数変数 -
gp.GRB.SEMICONTまたは"S"| 0またはlb以上ub以下の連続変数 -
gp.GRB.SEMIINTまたは"N"| 0またはlb以上ub以下の整数変数
-
-
name| 変数名の文字列- ASCII文字のみ可能で、空白は含まないことが推奨されている
- 必ず設定し、かつ、各変数で変数名の文字列が重複しないようにするとよい
- 設定してあげると、デバッグで役に立ちそう
-
gp.ModelクラスのオブジェクトのgetVarByName()メソッドの引数に変数名の文字列を指定すると、対応するgp.Varクラスのオブジェクトを返す
-
column| この変数が含まれる制約式たちと、各制約式でのこの変数の係数を表す、gp.Columnクラスのオブジェクト- 列生成法などの列方向モデリングしたいときに役に立つ
model_1.setObjective(2 * x + y, sense = gp.GRB.MAXIMIZE)
数理最適化問題model_1に、目的関数を設定します。そして、この目的関数を最小化したい場合はsense = gp.GRB.MINIMIZEを、最大化したい場合はsense = gp.GRB.MAXIMIZEを設定します。
c_1 = model_1.addConstr(x + y <= 4, name = "seiyaku_1")
c_2 = model_1.addConstr(x + 2 * y <= 6, name = "seiyaku_2")
数理最適化問題model_1に、2つのaddConstr()メソッドにより、2つの制約を加えています。また、このメソッドは、戻り値として、生成された制約式をgp.Constrクラスのオブジェクトにて返すので、返された2つの変数のオブジェクトをc_1やc_2に代入しています。
addConstr()メソッドでのnameの設定の注意点は、addVar()のときと同じです。gp.ModelクラスのオブジェクトのgetConstrByName()メソッドの引数に制約名の文字列を指定すると、対応するgp.Constrクラスのオブジェクトを返します。
model_1.optimize()
数理最適化問題model_1のoptimize()メソッドにより、解を求める計算をします。
if model_1.Status == gp.GRB.OPTIMAL:
「数理最適化問題model_1のoptimize()メソッドを実行した結果、最適解が得られていれば」という意味のif文です。
gp.ModelクラスのオブジェクトのStatus属性のうち、判定によく使われる値は以下のとおりです。
-
gp.GRB.OPTIMAL| 最適解が得られている -
gp.GRB.INFEASIBLE| 実行不可能と判定されている- 制約式を満たす解が存在しないという意味
-
gp.GRB.UNBOUNDED| 非有界と判定されている- 最小化問題で目的関数値がマイナス無限大まで小さくできてしまう、または、最大化問題で目的関数値がプラス無限大まで大きくできてしまうという意味
-
gp.GRB.INF_OR_UNBD| 実行不可能または非有界と判定されている- どういうときにこの属性値になるのか知りません
-
gp.GRB.TIME_LIMIT| 設定した計算時間の上限に達している-
model_1.optimize()よりも手前で、例えばmodel_1.Params.TimeLimit = 10としておくと、計算時間が10秒で打ち切られるようになります
-
x_opt = x.X
y_opt = y.X
gp.VarクラスのオブジェクトのX属性には、対応する数理最適化問題の変数の解の値が入っており、これを取得してPythonの通常の変数x_optとy_optに代入しています。
val_opt = model_1.ObjVal
gp.ModelクラスのオブジェクトのObjVal属性には、解の目的関数値が入っており、これを取得してPythonの通常の変数val_optに代入しています。
なお、model_1.optimize()して解が得られていないのにx.Xやmodel_1.ObjValを実行するとエラーになります。if model_1.Status == gp.GRB.OPTIMAL:という処理を書いているのはそのためです。
より詳しい公式ドキュメント類のありか
-
リファレンスマニュアル
スタート → Gurobi 8.0.1 (win64) → Gurobi Reference Manual (8.0.1)
(または、 C:\gurobi801\win64\docs\refman\refman.html ) -
Python API詳細
リファレンスマニュアル → Python® → Next: Python API Details -
Pythonインターフェースでの定数一覧
C:\gurobi801\win64\docs\refman\py_constants.html
(gp.GRB.定数名でアクセス) -
パラメーター一覧
C:\gurobi801\win64\docs\refman\parameters.html
(Pythonの場合、オブジェクト名.Params.パラメーター名でアクセス) -
属性一覧
C:\gurobi801\win64\docs\refman\attributes.html
(Pythonの場合、オブジェクト名.属性名でアクセス)
余談
Python(というかJava以外のだいたいの言語)は演算子のオーバーロードをサポートしているので、このサンプルでのsetObjective()やaddConstr()の引数のように、コードを数式に近いものにすることができ、見やすいです。そういう理由から、Javaインターフェースを使うことはお勧めしません。