【Python】漸化式で実装する動的計画法（DP）

概要

本稿では AtCoder の DP まとめコンテスト で公開されている練習問題を用いて、Python による動的計画法（Dynamic Programming：DP） の実装方法を紹介する。C++ を用いた実装については以下の記事が非常にわかりやすい。

• 動的計画法超入門！ Educational DP Contest の A ～ E 問題の解説と類題集
• 典型的な DP (動的計画法) のパターンを整理 Part 1 ～ ナップサック DP 編 ～

動的計画法（DP）

まず DP の流れを以下に説明する。

0） 与えられた問題を $N$ 回の繰り返し問題に分割する。
1） 1 回目の最適解を求める。
2） 1 回目の最適解をもとに 2 回目の最適解を求める
3） 2 回目までの最適解をもとに 3 回目の最適解を求める
4） 3 回目までの最適解をもとに 4 回目の最適解を求める
（中略）
n） n-1 回目まで最適解をもとに n 回目の最適解を求める

このように、繰り返される部分問題の最適解を、それより前の問題の最適解をもとに求めるアルゴリズムが DP である。DP は漸化式を用いると実装しやすい。

実装の流れ

本稿では、以下の流れで DP を実装する。

1） DP 配列を用意する
2） 初期条件を入力する
3） 漸化式にしたがって DP を実装する
4） DB 配列の末尾を出力させる

A 問題

問題概要

番号 $ 1 $ 〜 $ N $ の足場がある。足場 $ i （1 ≦ i ≦ N） $の高さは $ h[i] $ である。足場 $ i $ から 足場 $ j $ への移動では $ | h[i] - h[j] | $ のコストがかかる。足場 $ i $ へ移動できるのは、足場 $ i-1 $ と $ i-2 $ のみである。足場 $ 1 $ から足場 $ N $ への移動に必要な最小コストを求めよ。

制約

• $ 2 ≦ N ≦ 10^5 $
• $ 1 ≦ h[i] ≦ 10^4 $

漸化式

足場 $ 1 $ から $ i $ への移動に必要な最低コストを $ dp[i] $ とおく。足場 $ i $ へ移動する方法は、足場 $ i-1 $ から移動する方法と足場 $ i-2 $ から移動する方法がある。DP では、直前の足場に移動するまでの最適解がわかっていることを前提に漸化式を立てる。すなわち、足場 $ i-1 $ から移動するコストと足場 $ i-2 $ から移動コストを比べて、低いほうが $ dp[i] $ となる。

$$
dp[i] = \begin{cases}
0 & (i = 1) \\
h[2] - h[1] & (i = 2) \\
min(dp[i-2]+|h[i]-h[i-2]|,dp[i-1]+|h[i]-h[i-1]|) & (i ≧ 3) \
\end{cases}
$$

実装

実装例

# 入力読み込み
N = int(input())
h = list(map(int,input().split()))

# DP 配列を用意
# dp[i] には i 番目の足場にたどり着くために必要な最低コストを入れる
dp = [0]*N

# 初期条件を入力
dp[0] = 0
dp[1] = abs(h[1]-h[0])

# 漸化式にしたがって DP を実装する
for i in range(2,N):
  # i を現在いる足場と考える。
  # i 番目の足場へ行く方法として i-i 番目からのジャンプと i-2 番目からのジャンプがある
  # 2 通りの行き方のうちコストの少ない方を dp[i] とする
  dp[i] = min(dp[i-2]+abs(h[i]-h[i-2]),dp[i-1]+abs(h[i]-h[i-1]))

# dp 配列の末尾が N 番目の足場にたどり着くために必要なコストとなる
print(dp[-1])

B 問題

問題概要

番号 $ 1 $ 〜 $ N $ の足場がある。足場 $ i （1 ≦ i ≦ N） $の高さは $ h[i] $ である。足場 $ i $ から 足場 $ j $ への移動では $ | h[i] - h[j] | $ のコストがかかる。足場 $ i $ へ移動できる足場は、$ i-1 $ 、 $ i-2 $ 、$ ... $、 $ i-K $ の $ K $ 個である。足場 $ 1 $ から足場 $ N $ への移動に必要な最小コストを求めよ。

制約

• $ 2 ≦ N ≦ 10^5 $
• $ 1 ≦ K ≦ 10^2 $
• $ 1 ≦ h[i] ≦ 10^4 $

実装

A 問題と同様に $ dp[i] $ をおく。 A 問題では $ dp[i] $ へ移動する方法が 2 通りしかなかったが、今回は $ K $ 通りある。$ K $ 通りの経路のうち最小コストが $dp[i]$ となる。

実装例

# 入力読み込み
N,k = map(int,input().split())
h = list(map(int, input().split()))

# DP 配列を用意
# dp[i] には i 番目の足場にたどり着くために必要な最低コストを入れる
dp = [0] * N

# 初期条件を入力
dp[0] = 0

# 漸化式にしたがってループを回す
for i in range(1,N):
    # i を現在いる足場と考える。
    # i 番目の足場へ行く方法は max(k,i-k) 通り ある。
    # それぞれの行き方にかかるコストを tmp （tmporary） にまとめる。
    tmp = []
    for m in range(max(0, i-k), i):
        tmp.append(abs(h[m]-h[i])+dp[m])      
    # tmp のうち最小コストを dp[i] とする
    dp[i] = min(tmp)

# dp 配列の末尾が N 番目の足場にたどり着くために必要なコストとなる
print(dp[-1])

C 問題

問題概要

太郎くんは $ N $ 日間の夏休みを過ごす。$ i　(1 ≦ i ≦ N)$ 日目の太郎くんは行動 $ A $、$ B $、$ C $ のどれかひとつをとることで、幸福度 $ a_i $、$ b_i $、$ c_i $ をそれぞれ得る。太郎くんが夏休みで得られる最大幸福度を求めよ。ただし太郎くんは二日連続で同じ行動は取らない。

制約

• $ 1 ≦ N ≦ 10^5 $
• $ 1 ≦ a_i,b_i,c_i ≦ 10^4 $

漸化式

$ i $ 日目に行動 $ A $、$ B $、$ C $ をして $ i $ 日目までに得られる最大幸福度をそれぞれ $ dp[i][0] $、$ dp[i][1] $、$ dp[i][2] $ とおく。二日連続で同じ行動を取らないことから $ dp $ の漸化式は以下のようになる。

$$
\begin{cases}
dp[i][0]=max(dp[i-1][1]+a_i,dp[i-1][2]+a_i) \\
dp[i][1]=max(dp[i-1][0]+b_i,dp[i-1][2]+b_i) \\
dp[i][2]=max(dp[i-1][0]+c_i,dp[i-1][1]+c_i)
\end{cases}
$$

初期条件として $ 0 $ 日目の幸福度を $0$ とおく。すなわち $ dp[0][0] = dp[0][1] = dp[0][2] = 0 $ である。

実装

実装例

# DP 配列を用意する
# 本問では i 日目の動作として「Aをやる」「Bをやる」「Cをやる」の3通りが考えられる
# それぞれの行動をするための最大幸福度をそれぞれの漸化式で求める
# i 日目に A、B、C をやるための最大幸福度は dp[i][0]、dp[i][1][1]、dp[i][2] とする
N = int(input())
dp = [[0]*3 for _ in range(n+1)]

# 初期条件を入力
dp[0][0] = 0
dp[0][1] = 0
dp[0][2] = 0

# 漸化式にしたがって DP を実行する
for i in range(1,N+1):
  a,b,c = map(int,input().split())
  dp[i][0] = max(dp[i-1][1]+a,dp[i-1][2]+a)
  dp[i][1] = max(dp[i-1][0]+b,dp[i-1][2]+b)
  dp[i][2] = max(dp[i-1][0]+c,dp[i-1][1]+c)

# 最終日までに得られる幸福度の最大値を求める
print(max(dp[-1]))

D 問題（ナップサック問題1）

問題概要

$ N $ 個の品物がある。品物 $ i $ は重さ $ w[i] $、価値 $ v[i] $ である。重さの総和が $ W $ 以下になるように品物を選ぶとき、選んだ品物の価値の総和の最大値を求めよ。

制約

• $ N ≤ 10^2 $
• $ W ≤ 10^5 $
• $ v[i] ≤ 10^9 $

漸化式

$ i $ 番目までの品物を重さ $ j $ 以下で選ぶ。選ばれる品物の価値の最大値を $ dp[i][j] $ とする。ここでは価値の総和が大きくなるように品物を選ぶ。$ i + 1 $ 番目の品物 （重さ: $ w $ 、価値: $ v $ ）が選ばれるのは、$ i $ 番目までの品物で重さ $ w $ を使って稼げる価値よりも $ i + 1 $ 番目の品物で稼げる価値 $v$ のほうが大きい場合である。すなわち、以下の不等式が満たされる場合に $ i + 1 $ 番目の品物を選ぶ。

$$
dp[i+1][j+w] ≤ dp[i][j]+v
$$

この不等式に基づき、以下の漸化式が立てられる。

$$
dp[i+1][j+w] = max(dp[i][j]+v,dp[i][j+w])
$$

実装

実装例

# 入力読み込み
N,W = map(int,input().split())

# DP 配列用意
# i 番目までの品物を重さ j 以下で選ぶ場合、品物の総和の価値の最大値を dp[i][j] とする
dp = [[0]*(W+1) for _ in range(N+1)]

# 漸化式にしたがって DP を実行する
# i+1 番目の品物（重さ:w、価値:v）を選ぶのは 
# i 番目までの品物で重さ w を使って稼げる価値より i+1 番目の品物で稼げる価値 v のほうが大きい場合である
for i in range(N):
    dp[i+1] = dp[i].copy() #上書きを防ぐために .copy() は必須
    w,v = map(int,input().split())
    for j in range(W+1-w): 
        dp[i+1][j+w] = max(dp[i][j]+v,dp[i][j+w])

# dp 配列の末尾が N 番目までの品物から重さ W 以下で選ぶ場合の品物の価値の最大値となる。
print(dp[-1][-1])

E 問題（ナップサック問題2）

問題概要

$ N $ 個の品物がある。品物 $ i $ は重さ $ w[i] $、価値 $ v[i] $ である。重さの総和が $ W $ 以下になるように品物を選ぶとき、選んだ品物の価値の総和の最大値を求めよ。（D問題と同じ）

制約

• $ N ≤ 10^2 $
• $ W ≤ 10^9 $
• $ v[i] ≤ 10^3 $

漸化式

D 問題と同じ漸化式で実装すると、DP 配列の長さが最大で $10^9$ になるため計算時間が膨大にかかる。計算時間短縮のために別の漸化式を立てる。

$ i $ 番目までの品物を価値 $ j $ で選ぶ。選ばれる品物の重さの総和の最小値を $ dp[i][j]$ とする。全品物の価値の総和は $ N × v[i] ≤ 10^5 $ であるから、dp 配列の長さは最大で $10^5$ となる。したがって $ dp[N][j]$ を末尾から調べ、初めて $W$ 以下になる $ j $ を答えとして求めれば制限時間内に計算を終えられる。

ここでは重さの総和が小さくなるように品物を選ぶ。$ i + 1 $ 番目の品物 （重さ: $ w $ 、価値: $ v $ ）が選ばれるのは、$ i $ 番目までの品物で価値 $ v $ を節約して減らせる重さが $ w $ 以下の場合である。すなわち、以下の不等式が満たされる場合に $ i + 1 $ 番目の品物を選ぶ。

$$
dp[i][j-v] + w ≤ dp[i+1][j]、　0 ≤ j-v
$$

この不等式に基づき、以下の漸化式が立てられる。

$$
dp[i+1][j] = min(dp[i][j], dp[i][j-v] + w)
$$

実装

実装例

import math
#  入力読み込み
N, W = map(int, input().split())

# dp 配列の用意
# i 番目までの品物から価値 j で選べる品物の重さの総和の最小値を dp[i][j] とする
# 品物の価値の総和の最大値を L とする。
# 今回は価値 1000 の品物が 100 個用意される可能性を考えて L = 100000 とする
# 重さの最小値に無限大を入れて初期化する
L = 100000
dp = [[math.inf]*(L+1) for _ in range(N+1)]

# 初期条件を入れる
dp[0][0] = 0

# 漸化式にしたがって DP を実行する
# ここでは重さの最小値が小さくなるように品物を選ぶ
for i in range(N):
    w, v = map(int, input().split())
    for j in range(L+1):
        # i+1 番目の品物 （重さ:w、価値:v）が選ばれるのは
        # i 番目までの品物で価値 v を節約して減らせる重さが w 以下のとき
        if j - v >= 0: 
            dp[i+1][j] = min(dp[i][j], dp[i][j-v] + w)
        else:
            dp[i+1][j] = dp[i][j]

# dp[N][j] を先頭から調べたとき、最後に W 以下になる j を答えとする
for i, d in enumerate(dp[N]):
    if d <= W:
        maxv = i
print(maxv)

F 問題（LCS）

問題概要

文字列 $s$ および $t$ について。 s の部分列かつ t の部分列であるような文字列のうち最長のものをひとつ求めよ。ただし文字列 $X$ から 0 個以上の文字を取り除き、残りの文字を元の順序で連結して得られる文字列を $X$ の部分列とする。
この部分列は最長共通部分列 (Longest Common Subsequence: LCS) ともいわれる。

制約

• $s$ および $t$ は英小文字からなる 3000 字以下の文字列である

漸化式

Python のルールに従い $S$ の $i+1$ 文字目を $S[i]$ とする。$S$ を $i+1$ 文字目、$T$ を $j+1$ 文字目までみた時の LCS の長さ を $dp[i][j]$ とする。例えば $dp[2][3]$ は $S$ を 3 文字目、$T$ を 4 文字目まで見たときの LCS の長さとする。 ここでは $dp[i+1][j+1]$ を考える。　$S[i] = T[j]$ のとき $S[i]$ は LCS に含まれるが、そうでないときは $S[i]$ と $T[j]$ の少なくとも一方は LCS に含まれないので、以下のような漸化式を立てられる。

$$
\begin{cases}
dp[i+1][j+1]=dp[i][j] + 1 & (S[i] = T[j])\\
dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]) & (S[i] ≠ T[j])
\end{cases}
$$

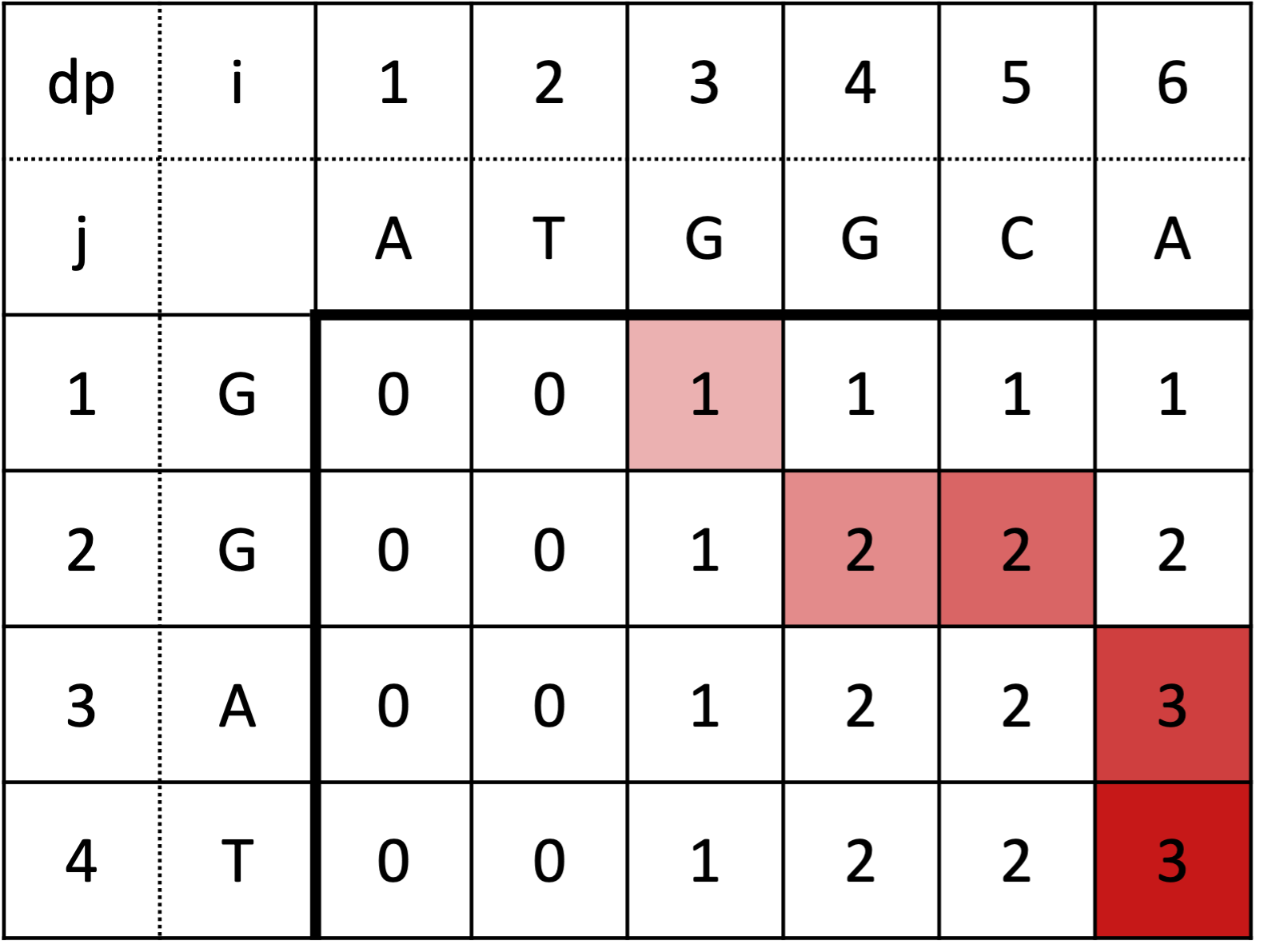
これで LCS の長さを求める。LCS は dp 配列をもとに後ろから復元することができる。 下図に $S=$ ATGGCA、$T=$ GGAT の例をあげる。LCS の最後尾は dp 配列の右下のほうに存在するので $dp[6][4]$ から探索する。
復元時は $dp[i][j]$ を考える。$s[i-1]=t[j-1]$ のとき、LCS の最後尾には $s[i-1]$ を使って次に $dp[i-1][j-1]$ を調べればよい。そうでない場合は、少なくともどちらか一方は LCS に含まれないため dp の値が減らないほうを探索すればよい。この方法で、図では赤色が濃いマスからうすいマスへ dp 配列を調べると LCS が GGA であることがわかる。

実装

実装例

S = input()
T = input()
# S を i+1 文字目、T を j+1 字目までみた時の LCS の長さ を dp[i][j] とする
# 例えば dp[2][3] は S を 3 文字目、T を 4 文字目まで見たときの LCS の長さ
dp = [[0]*(len(T)+1) for _ in range((len(S)+1))] 

# DP 配列作成
for i in range(len(S)):
	for j in range(len(T)):
		# dp[i+1][j+1] を考える
		# S[i] == T[j] のとき、S[i] は LCS に含まれる
		if S[i] == T[j]:
			dp[i+1][j+1] = dp[i][j] + 1
		# S[i] == T[j] でないとき、S[i] と T[j] の少なくとも一方は LCS に含まれない
		else:
			dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j])

# LCS を後ろから求める
# i,j,l の初期化
ans = [] # LCS（後ろから求めるので最後に反転させる）
i = len(S) 
j = len(T)
l = dp[i][j]

# dp[i][j] から dp の値 l がなるべく減らないルートを辿れば LCS を後ろから求めることができる
while l > 0:
	# S[i-1] == T[j-1] のとき、S[i-1] は LCS に含まれるので ans に追加し、次に dp[i-1][j-1] を調べる
	if S[i-1] == T[j-1]:
		ans.append(S[i-1])
		i -= 1
		j -= 1
		l -= 1
	# S[i-1] == T[j-1] でないとき、dp[i-1][j] と dp[i][j-1] のうち dp の値が減らないほうを調べる
	elif dp[i][j] == dp[i-1][j]:
		i -= 1
	else:
		j -= 1
	if l <= 0:
		break
print(''.join(reversed(ans)))

G 問題

こちらで解説。

H 問題

問題概要

. または # からなる 2 次元のマスがある。. のマスのみを辿って右または下に移動するとき、左上のマスから右下のマスへの行き方は何通りあるか求めよ。

制約

• 行数および列数は 2 以上 1000 以下
• 左上のマスは必ず .

漸化式

右または下にしか移動でいないことから c 列 r 行目への行き方を $dp[r][c]$ とすると、以下の漸化式が立てられる。

$$
dp[r][c] = dp[r][c-1] + dp[c-1][r]
$$

実装

マス目をノードと考え、クラス Node を定義する。順番に各ノードへの行き方を求めていけばよい。参考

実装例

import sys

# クラスを宣言
# マス目をノードとおく
class Node:
    # コンストラクタを宣
    def __init__(self, row, col):
        self.col = col # 列を定義
        self.row = row # 行を定義
        self.way = 0 # col 列 row 行目への行き方

    def __repr__(self):
        return F'<Node({self.col+1}, {self.row+1}): way={self.way}>'

def main():
    
    # mod を忘れずに
    mod = 10**9 + 7

    # 入力読み込み
    input = sys.stdin.readline
    H, W = map(int,input().split())
    # 地形を pic に格納
    pic = [ list(input())[:-1] for _ in range(H) ]

    # インスタンス（Node）を生成し nodes に格納する。
    nodes = [[Node(r,c) for c in range(W)] for r in range(H)]

    # 出発地である 1 列 1 行目の行き方を 1 通りとする
    nodes[0][0].way = 1

    # DP を実行
    # col 列 row 行目への行き方は col-1 列 row 行目と col 列 row-1 行目の行き方の合計
    for c in range(W):
        for r in range(H):
            if not ((r == 0) and (c == 0)):
                if pic[r][c] == '.':
                    nodes[r][c].way = (nodes[r - 1][c].way + nodes[r][c - 1].way)%mod
                    # print(nodes[r][c]) コメントアウトを外すと現在地を確認できる
                    # ちなみに c = 0 または r = 0 のとき 
                    # nodes[r-1][c] や nodes[r][c-1] で [] の中が -1 になってしまうが
                    # way メソッドの初期値を 0 に指定しているため計算は正しく行われる

    print(nodes[r][c].way)

# 実行の高速化
if __name__ == '__main__':
  main()