概要
この記事は、【Google Colabで学ぶ】データ可視化のデザイン の理解度を確認するための演習問題となっています。解説なども活用しながらデータの可視化をマスターしましょう!
第1問
データ可視化の目的として最も適切なものを(A)~(C)から1つ選びましょう
A.) 事前に定めた仮説に基づいて優位な差があるかどうかを調査・検定すること
B.) データ間の類似度にしたがってグループ分けし、元データでは捉えられなかった観点から傾向を理解すること
C.) 平均値などの統計量だけではつかめないデータの傾向を視覚的に捉え、データを理解しやすくすること
D.) 成果物が開発者の想定通りに挙動するかどうかをテストし、保守・運用に役立てること
第1問の正解・解説
正解は(C)です!
A.) 統計的仮設検定の説明です
B.) クラスタリングの説明です
D.) 単体・結合テストの説明です
第2問
グラフの軸で気を付けるべきポイント(A)~(D)のうち最も適切なものを1つ選びましょう
A.) データの理解を助けるために、軸の目盛りや掛け線は細かめに入れるのが良い
B.) ばらつきが大きい分布をグラフで表現する場合、データに0が含まれていても対数軸を使用するのが良い
C.) データの差を強調するために0以外の値を軸の始点とする場合は、値の大きさを錯覚しないよう読み手に伝えるとよい
D.) ヒストグラムはデータが密集している領域では特にビンを細かく設定するのが良い
第2問の正解・解説
正解は(C)です!
A.) 目盛りや掛け線はデータそのものを表しているわけではないため、細かく入れるとグラフの情報が伝わりにくくなります
B.) 0や負の数は対数化できないため、そのような値が含まれている分布は対数軸で表せません
C.) 必要に応じて軸の始点を何という値にしたのかを伝えると親切です。
D.) ヒストグラムのビンの間隔は等しくないと分布が分かりにくくなります
第3問
円グラフの作成で気を付けるべきポイントとして最も適切なものを(A)~(C)から1つ選びましょう
A.) 円グラフの扇形から割合の大小を読み取るのは難しいため、強調したい項目の扇形は赤色などでハイライトするとよい
B.) 円グラフはおしゃれなデザインをしているため、特に強調して表現したい場合は3Dなどを活用して目立たせるとよい
C.) 円グラフでは各項目の大小関係が分かりにくいため、凡例が少ない場合に使用するのがよい
第3問の正解・解説
正解は(C)です!
A.) 赤色などの暖色系は膨張色といわれ面積が大きくみえるような錯覚効果があります。円グラフのように面積で割合の大小を表現するようなチャートでは誇張して伝わることがあるため注意したほうが良いです。
B.) 3D円グラフの場合、画面手前側に見える円柱の側面が誇張されるため使用しないほうが良いとされています。一般的にヒトは三次元情報を二次元画像から認識するのが得意ではありません。
C.) 凡例が多い場合、各項目の大小関係が分かりにくくなります。
第4問
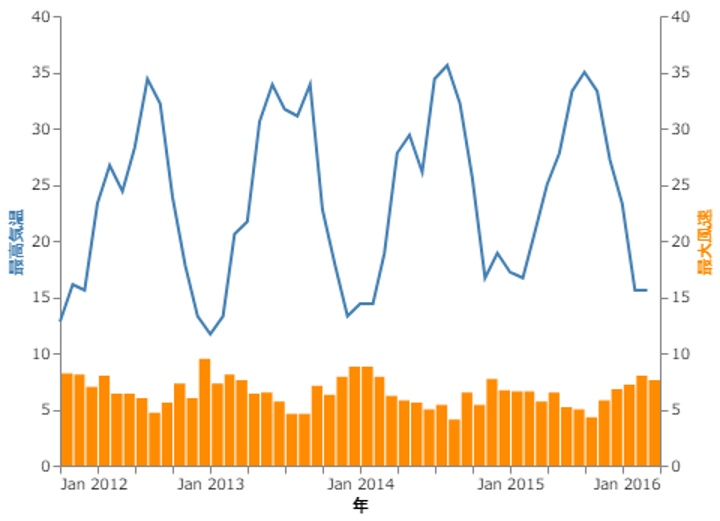
次のグラフで直したほうが良いポイントとして最も適切なものを(A)~(D)から1つ選びましょう
A.) 最高気温を正確に読み手に伝えるために目盛りの間隔を小さくしたほうがよい
B.) グラフの認知的負荷を下げるために最高気温と最大風速を同色で表現したほうがよい
C.) 最高気温と最大風速の目盛りの参照先を明確にするために、それぞれ別のグラフで表現したほうがよい
D.) 最大風速の大小を分かりやすくするために、最高気温40の目盛りと同じ高さに最大風速20の目盛りが来るように目盛りの高さ変更したほうがよい
第4問の正解・解説
正解は(C)です!
A.) 目盛りはデータそのものを表しているわけではないため、細かく入れるとグラフの情報が伝わりにくくなります
B.) 同色で表現すると最高気温と最大風速の区別がつかなくなります
D.) 実はこのグラフ、左軸の最高気温と右軸の最大風速では同じ高さで同じ目盛りの値が振られています。つまり左軸と右軸を間違えて参照しても読み手に誤解されにくいグラフとはなっていますが、選択肢のように目盛りの位置を変更すると左軸と右軸を間違えた際に値が誤解されやすくなります
他に直したほうが良いポイントとしては最高気温や最大風速に単位を入れることなどが挙げられます。
第5問
箱ひげ図について述べた文章(A)~(D)のうち最も適切なものを1つ選びましょう
A.) 中央値や四分位数を簡単な図形で表現できるため、統計の知識が全くない人に対しても図の見方を説明せずに分布の広がりを伝えることができる
B.) 箱ひげ図で表現される最大値よりも、さらに大きな値として外れ値が存在することがある
C.) 箱ひげ図を見れば全データの値を確認することができる
D.) 箱ひげ図で表現される箱の区間に平均値は必ず存在する
第5問の正解・解説
正解は(B)です!
A.) 統計の知識が全くない人に分布を説明するには丁寧な説明が必要です。中央値や四分位数といった統計量を使用しないヒストグラムなどを用いて表現したほうがよい場面もあります
B.) 箱ひげ図ではひげの上限が最大値です。(ひげの上限)=(第三四分位数)+1.5×(四分位範囲) であり、それ以上の値は外れ値となります
C.) 箱ひげ図は中央値・四分位数・最大値・最小値といった分布を表す統計量のなかでも重要なものしか表現していません。全データの値を確認できるグラフとしてジッタープロットや散布図などがあります
D.) 大きな分布の偏りや外れ値がある場合、箱の区間(四分位範囲)に平均値が存在しないこともあります
第6問
折れ線グラフについて述べた文章(A)~(C)のうち最も適切なものを1つ選びましょう
A.) 折れ線グラフで様々な凡例の時系列推移を比較したい場合は、色だけを変更した折れ線を別の凡例として十数本書き足しても問題ない
B.) 折れ線グラフで時系列推移の傾向を可視化したい場合は各時点の値をすべてグラフ中に書き込むとよい
C.) 折れ線グラフは各時点の値がプロットされ情報過多になることが多いため、目盛りの掛け線は消したほうがよい
第6問の正解・解説
正解は(C)です!
A.) 凡例が多い折れ線グラフはスパゲッティチャートといって凡例の参照が難しくなります。特に着目したい凡例のみをハイライトするなど、読み手に示唆が伝わりやすい作図を心掛けましょう
B.) 各時点のデータをグラフに書き込むと情報過多になります
第7問
散布図について述べた文章(A)~(D)のうち最も適切なものを1つ選びましょう
A.) 散布図は2つの変数の関係性を表すのに適しており、プロットの分布の形状さえ見れば平均・分散・共分散を正確に把握できる
B.) 散布図のプロットの大きさで3つめの変数の大小を表現したグラフはバブルチャートと呼ばれ、散布図より表現可能な情報が多く積極的に活用すべき
C.) 2変数の関係性を理解するのは難しいことが多いため、チャート内の領域別にどのようなデータがプロットされるかを説明する必要がある
D.) 散布図はデータ間の類似度を表現することができ、プロットが近傍にあるデータの類似度は必ず高い
第7問の正解・解説
正解は(C)です!
A.) 分布の形状だけで平均・分散・共分散は分かりません
B.) 3つの変数を同時に解釈するのは難しいため積極的な使用は推奨しません。主題や論点を分解し、なるべく1つのグラフからは1つのメッセージだけを伝えることを意識しましょう
D.) 散布図の軸がデータの性質をすべて表しているとは限らないため、近傍にあるデータの類似度が必ず高いとは限りません。散布図の軸として表現されていない別の変数・要因で全く異なる性質を取っている可能性も考慮しましょう