RWA (Recurrent Weighted Average) とは?

論文 (Machine Learning on Sequential Data Using a Recurrent Weighted Average) はこちら
上図の c が RWA のモデル概略図です (a は通常の LSTM、b はアテンション付きの LSTM)。
RWA とは、系列データを扱う再帰的ニューラルネットワーク (Recurrent Neural Networks; RNN) の派生のひとつです。
提案論文中では、RNN の実装としてよく使用されている LSTM と比較して、
- 精度が良い
- 収束が速い
- パラメータ数が少ない
と、良いことずくめのことが書いてあります。
その主張の強さとアーキテクチャの簡明さに驚き、また、現在ほぼデファクトスタンダードとなっている LSTM を本当に上回ることができるのか疑問に思ったため、今回はRWA の Keras 実装を少し書き直して、論文中の実験のいくつかを再現してみました。
RWA のアーキテクチャ
※実験結果を見たい方はこのセクションは飛ばして問題ありません
RWA は Attention を一般化し、再帰的に定義し直すことで RNN の構造に組み込んだものである、と考えることができます。
言い換えれば、(RNN における) attention とは、RWA の特殊な場合です。
もう少し詳しく見ていきましょう。
LSTM に限らず、あらゆる RNN は系列データを処理するネットワークです。
系列データはマルコフ過程 (=現在の状態は現在のデータと過去の状態でのみ決まる) の仮定をおくことで処理が容易になるため、RNN では「現在のデータ」と「過去の状態」を入力として、「現在の状態」を出力するようにして再帰的にモデル化されます。
式で書けば、
$$
h_t = Recurrent(x_t, h_{t-1})
$$
です。$h_t$ が現在 t の状態、$x_t$ が現在のデータ、$h_{t-1}$ は過去の状態です。
この関数 $Recurrent$ をニューラルネットワークで実装したものが RNN であり、$Recurrent$ 関数に各種のゲートを導入して複雑化したものが LSTM となります。1
しかし、一番上の図を見るとわかるように、Attention モデルは再帰的に定義されているわけではないため、関数 $Recurrent$ の形式で表すことはできません。2
RWA は attention を過去の状態の移動平均だと考え、さらに式を等価に変形することで、$Recurrent$ 関数の形式に帰着させます。
具体的に書けば、RWA では次のように過去の状態の移動平均を取ります:
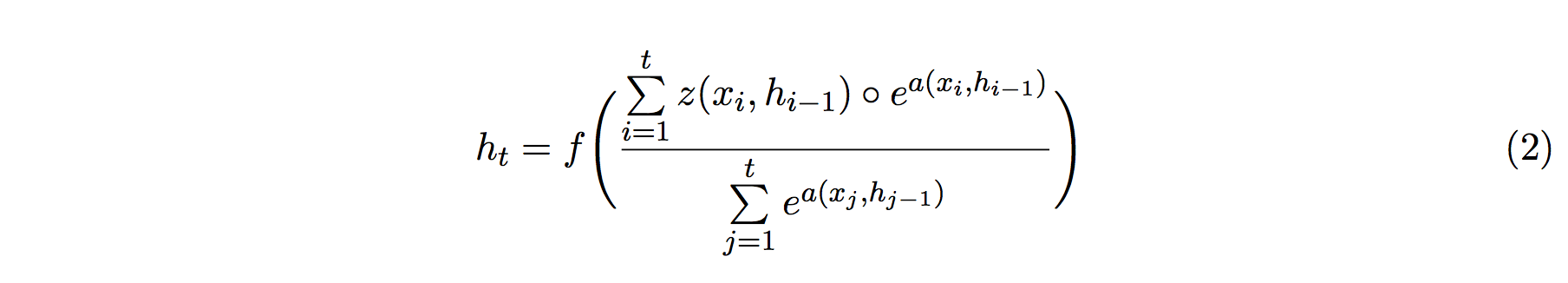
f は適当な活性化関数であり、z が再帰的に状態を変換していく項、そして a が過去の状態をどれだけの重きを置いて平均するかを支配します (a が attention に対応します)。
この式のままだと、Σに「過去の状態を 1 から t まで足し合わせる」操作が含まれているため、再帰的だとは言えません。
どうにかして、「一つ前の状態」だけで (2) 式を定義し直したいです。
ここで、(2)式の f の内部を分母 d と分子 n に分けてみます。
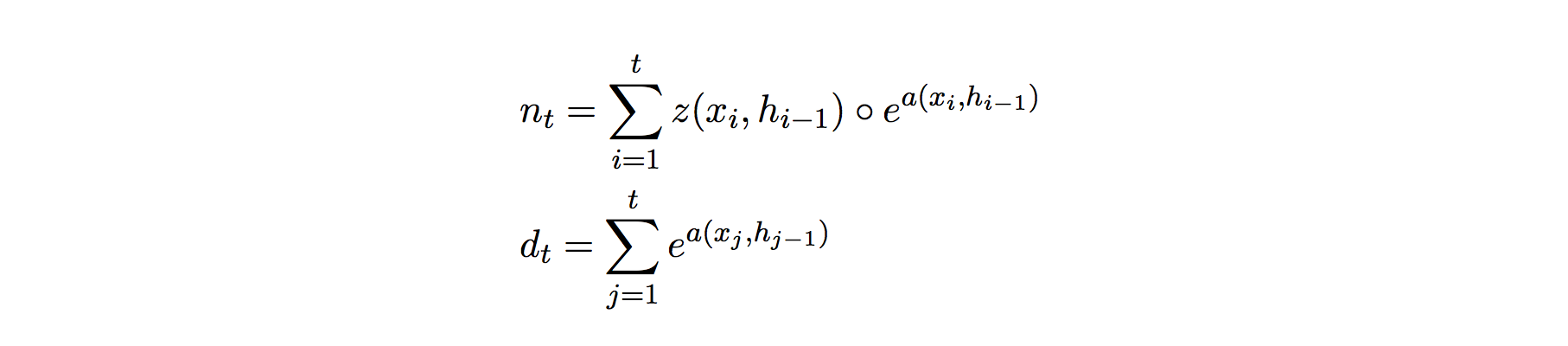
すると、n と d は累積和であることがわかるため、次のように書き直すことができます:
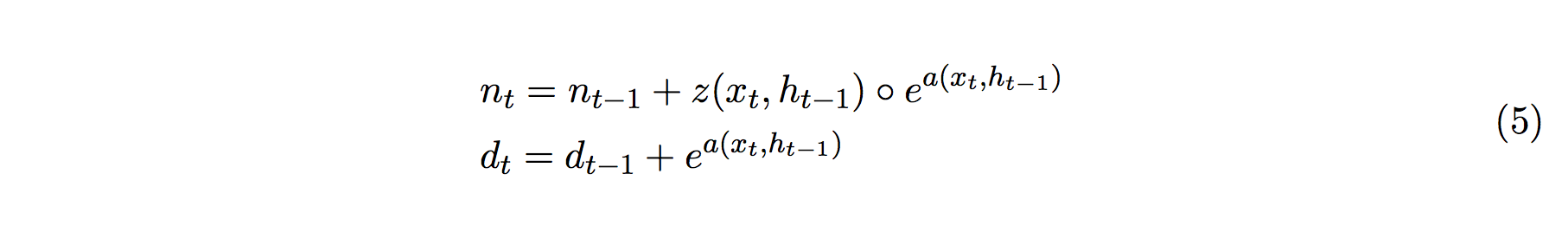
この時点で、n と d が一つ前の時点にのみ依存した形式に変形できています。
エッセンスはこれですべてです。
あとは z を普通の RNN とは少し変えて入力だけを見る項 u (つまりembedding) と状態も見る項 g に分割した式
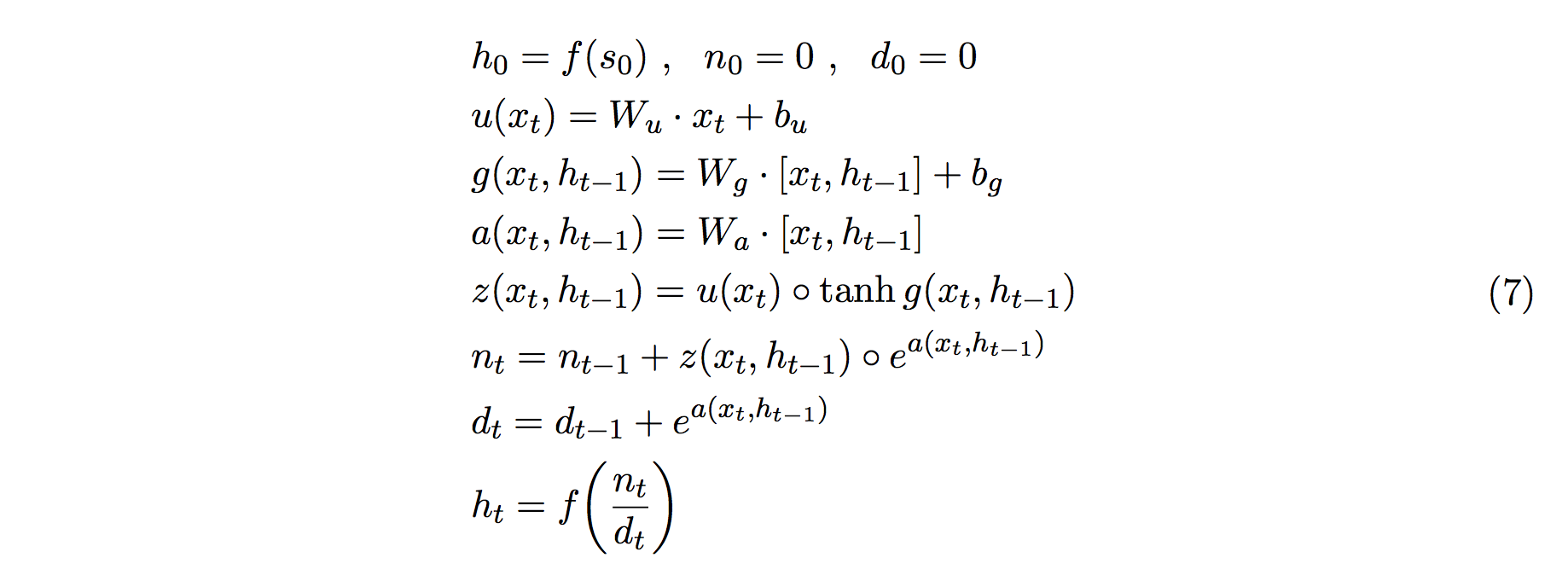
が RWA の数理となります。3
RWA は最もシンプルな RNN とほぼ同じ構造をしています。
RWA はもともと「過去のすべての状態を参照する」形式から出発しているため、LSTM のように内部に Forget gate や output gate がなくとも、いつでも過去の状態を参照して状態を更新できることが期待されます。
実装
第三者が公開している RWA の Keras 実装を return_sequences パラメータが有効となるように修正したコードで実験をおこないました。
修正したコードや実験・可視化スクリプトはこちら
(return_sequences は Keras の Recurrent Layer で一番最後の状態だけではなく過去の状態すべての履歴を出力するかどうかを設定できるパラメータです。これがないとあとで状態の可視化ができません)
実験
論文中で言及されている実験のうち、実装が最も容易な
- Classifying by Sequence Length
- Adding Problem
の二種類で実験をおこないました。
Classifying by Sequence Length
「与えられた系列データの長さが、ある長さを超えているかどうか?」を判定する問題です。
長さが 0 以上 1000 以下の範囲でランダムに変わるベクトルを用意して、そのベクトルの長さが 500 を超えていれば1,そうでなければ 0 と判定させます。
ベクトルの各要素の値は適当に正規分布から取ってきて埋めます (注意:ベクトルの要素値は今回の問題に関係ありません。今回の問題に関係あるのはベクトルの長さです)
目的関数は binary_crossentropy です。
なお、論文ではミニバッチサイズを100として実験されていましたが、系列長の異なるデータを同じバッチに組み込むことが面倒だったため、この問題の実験ではバッチサイズ1としています (結構時間かかります。以下の結果はGPU使って12時間くらいで得られました)。
実験結果は次のとおりです
(縦軸:精度 (高い方が良い)、横軸:エポック数)
- 論文の結果

- 今回実験した結果
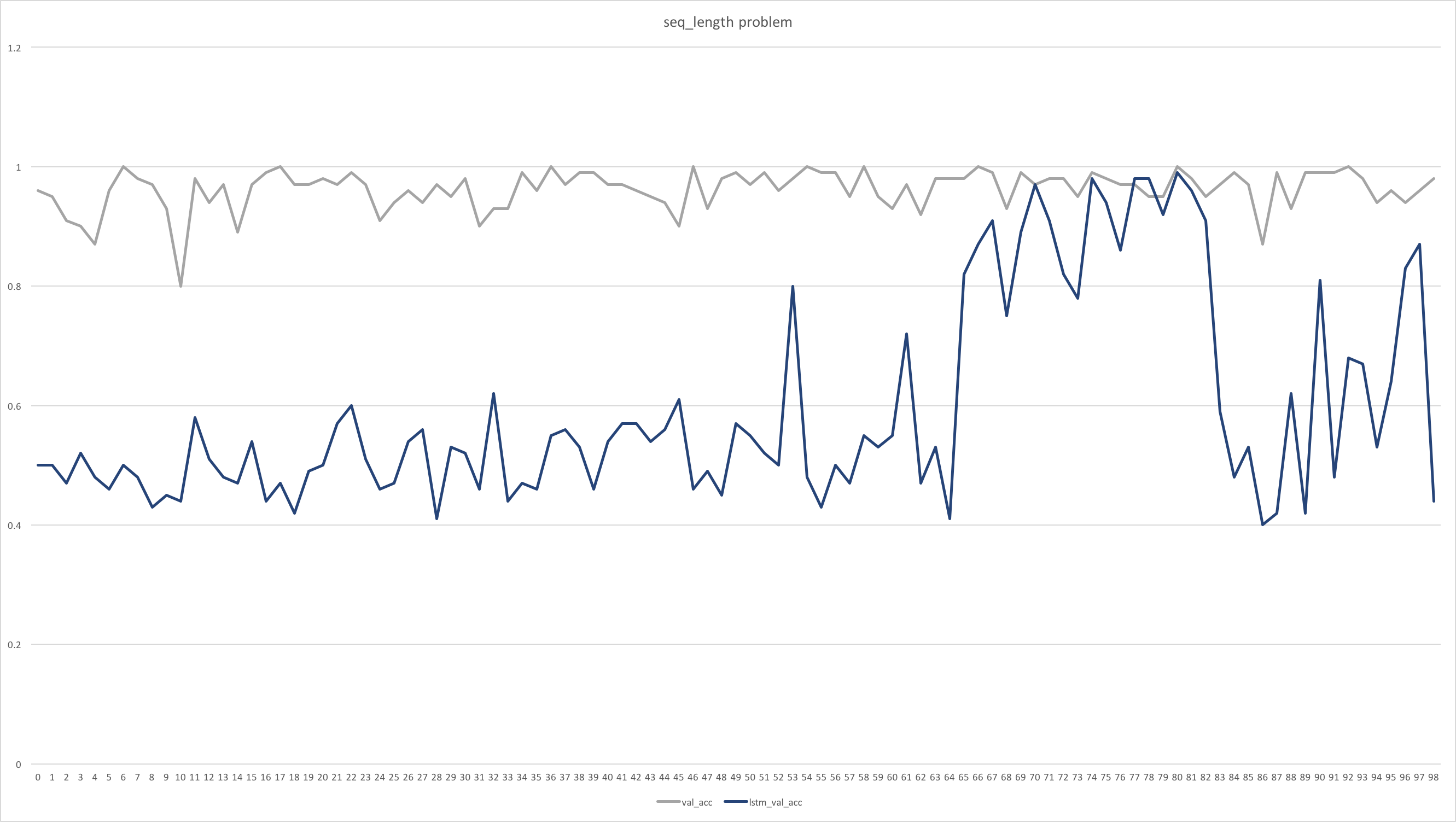
時間の都合上、LSTM が学習途中のままですが、RWA の収束が圧倒的に速いという点では論文の結果と同じでした (何サンプル学習して収束するのかについては、バッチサイズが違うためなんとも言えません)。
データを処理している最中に、RWA の状態がどのようになっているのか気になったため、そちらもプロットしてみました。
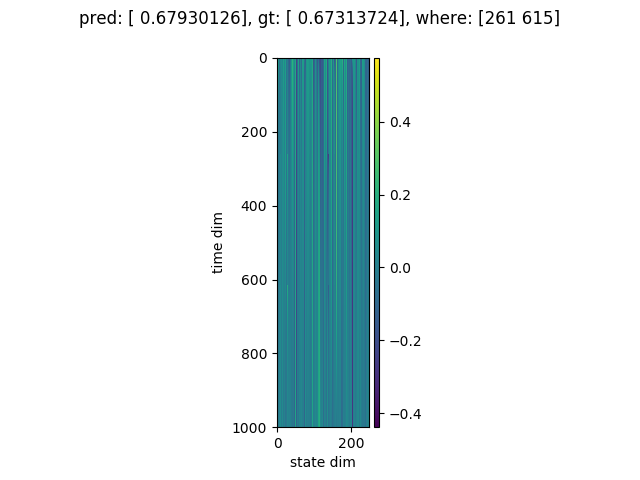
縦軸が時間の次元、横軸が状態の次元(250) です。
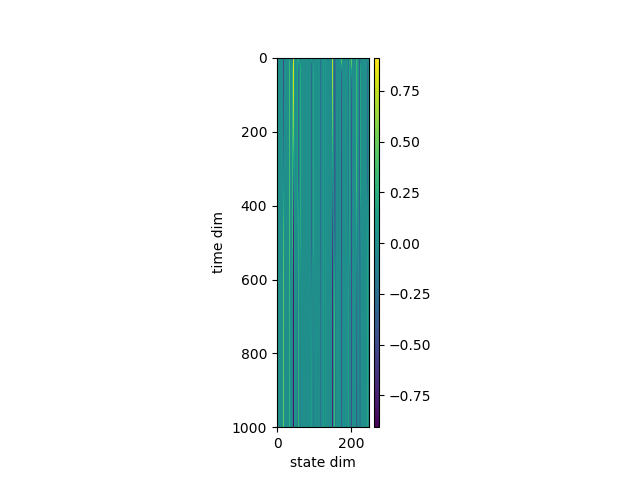
上図は系列長が 1000 の (つまり予測結果は「1」になってほしい) 例です。この場合は正しく予測できていました。
状態のプロットを見ると、どうやら系列長が500に近いあたりで状態が切り替わり、全体としては時間方向にグラデーションがかかったような状態であるらしいことがわかります。
どうやら正しく学習できていそうです。
系列長の長さを色々変えてテストしてみましたが、やはり系列長が500近辺で精度が強烈に悪化する一方、極端に短かったり長かったりする系列に関しては精度が100%でした。(上図も極端に系列長が長い例です)
Adding Problem
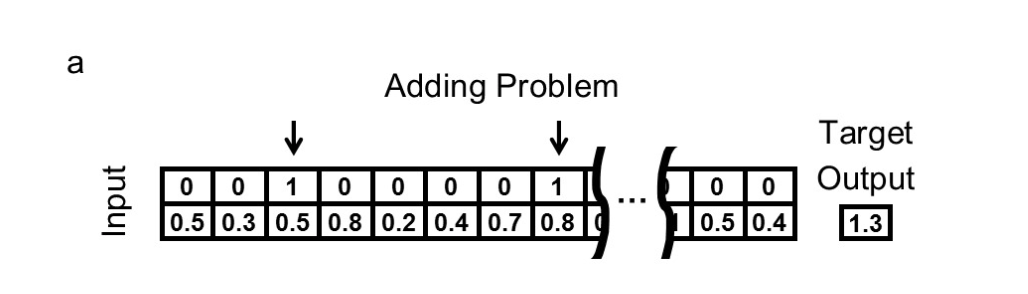
「適当な長さのベクトルを用意して、そのうちランダムに選ばれた二箇所の値を足す」問題です。
モデルに与えられるデータは、長さ n のベクトルが二個です。
片方は実数ベクトルで、もう片方は2箇所だけ1が立っていて残りは0のベクトルです。
1が立っているところの実数を足し合わせるように学習をさせます。
目的関数は MSE です。
こちらの問題は、論文通りミニバッチサイズ100として実験しました。
実験時間はGPUを使って1時間かからないくらいです。
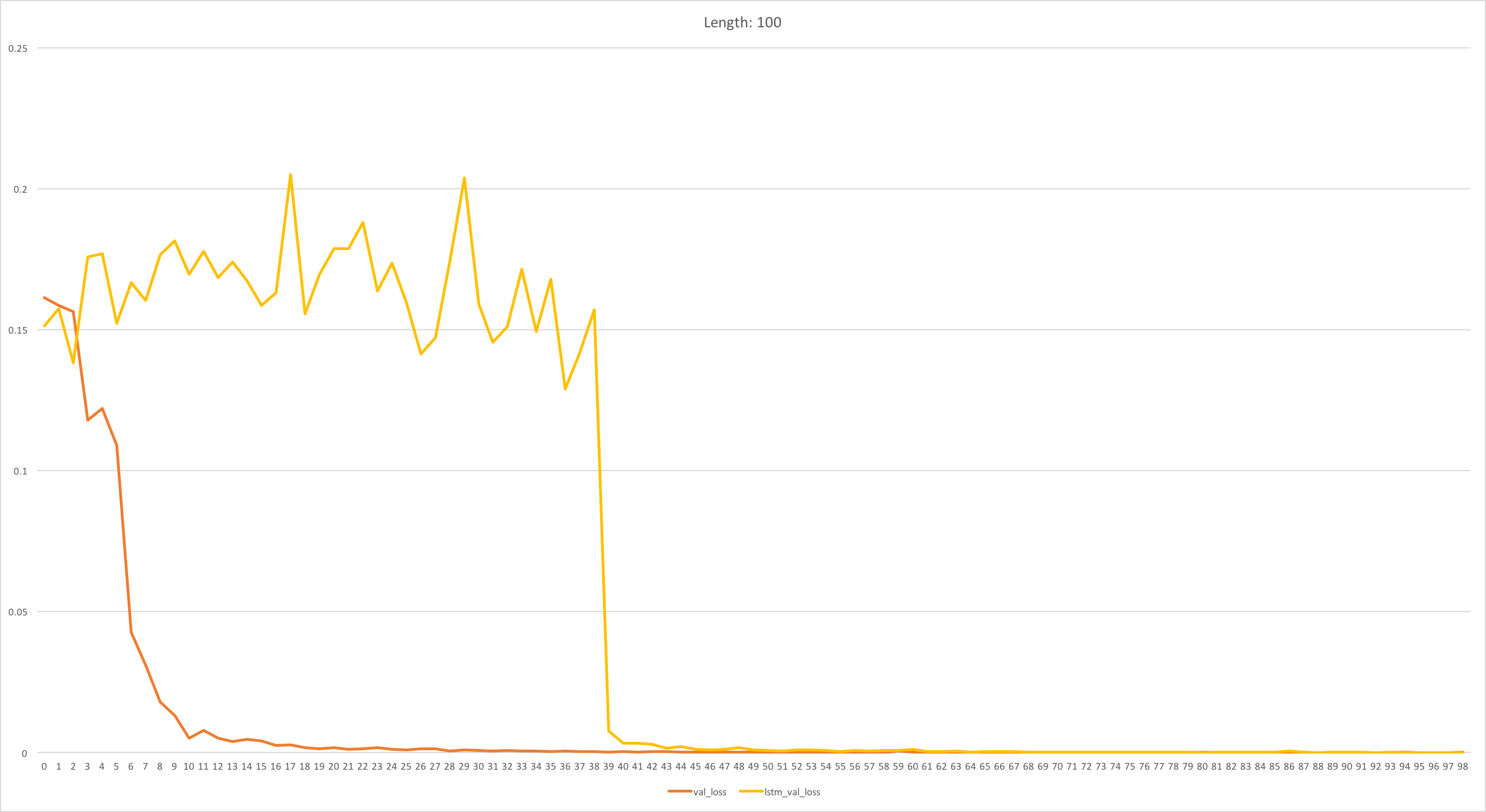
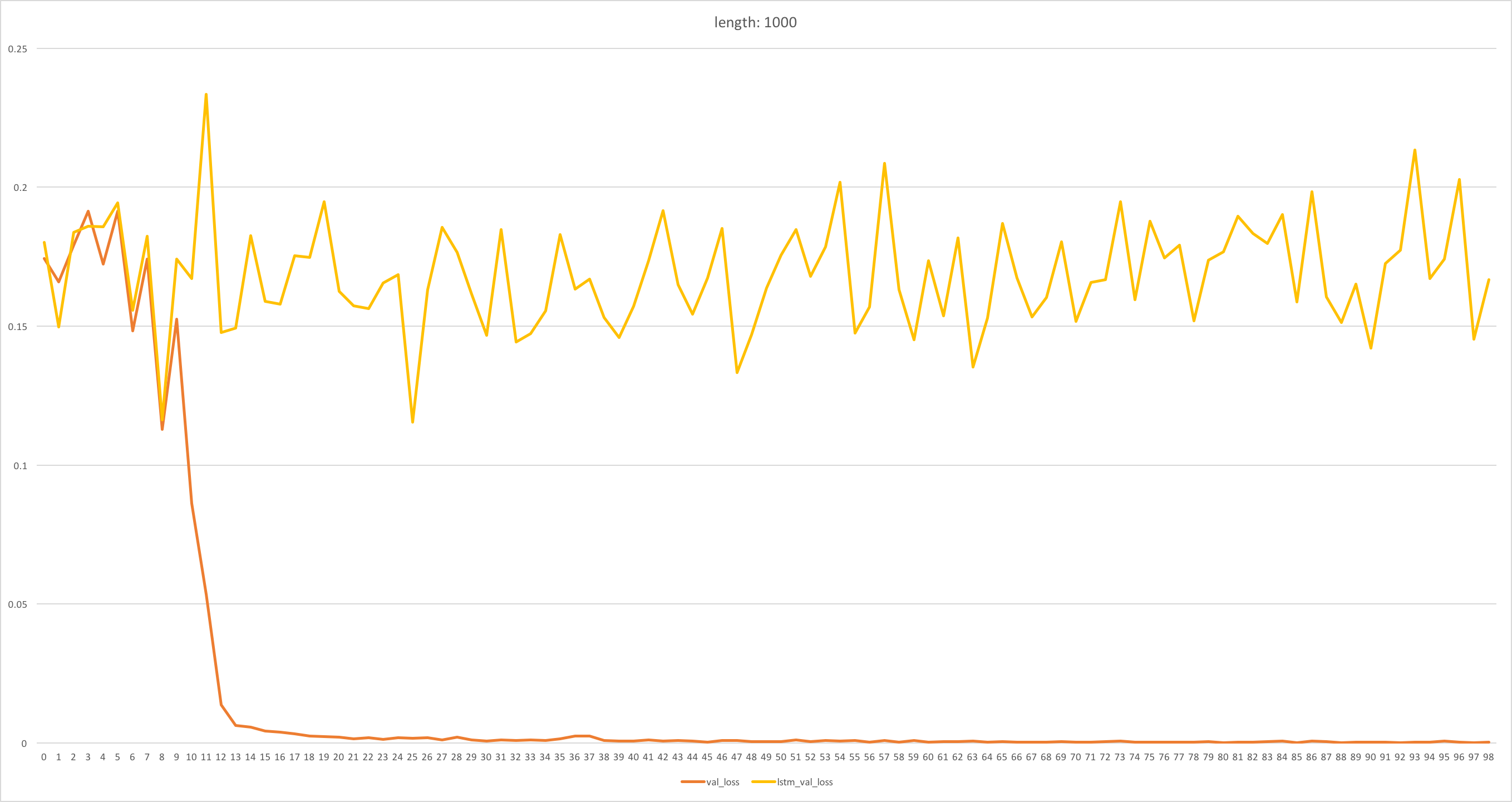
実験結果は次のとおりです
(縦軸:MSE (低い方が良い)、横軸:エポック数)
- 論文の結果

横軸のスケールが変わっています (1epoch=100batchで実験したので、私の実験結果の横軸の値は100倍すると元論文と同じスケールになります) のでご注意ください。
RWA に関しては論文の結果が再現できました。
LSTM は、長さ100の場合論文と同じ結果が得られましたが、長さ1000の場合うまく学習できていません。
元論文の結果の LSTM の収束の様子と比較すると、長さ1000の系列では追加であと100epochほど学習を回せば精度が上がり始めるでしょうか。
RWA は「ハイパーパラメータや初期化の設定をいじらなくても、(試した範囲だと) どの問題も解ける」という点も主張しているため、むしろ RWA だけが一発で論文の結果を再現できたのは追試としてはより望ましいかもしれません。
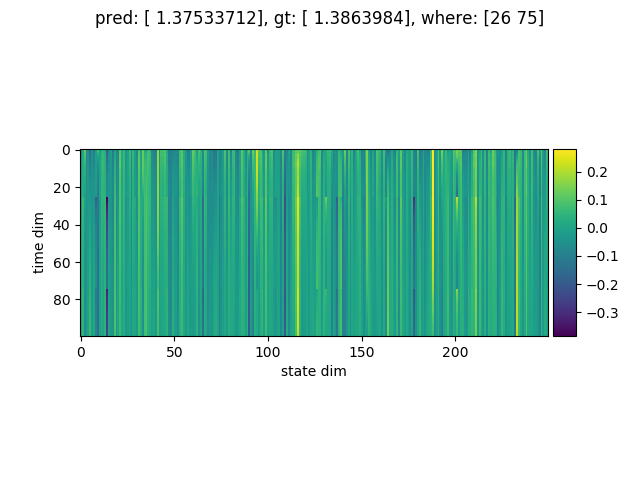
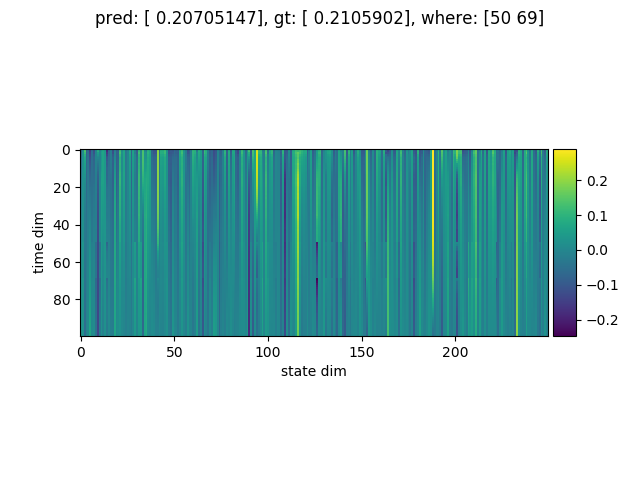
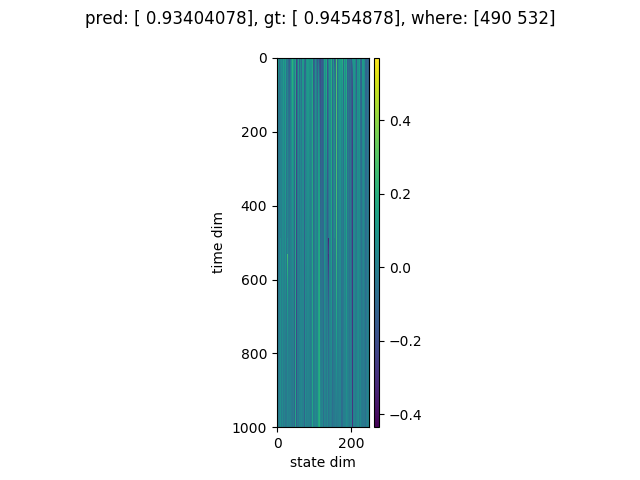
RWA の状態は次のとおりです (1つのグラフがひとつのサンプルに対応しています)
縦軸が時間(100または1000)、横軸が状態の次元(250) です。
図の上に書いてある where は、正解のフラグがどの位置に立っていたかのデータです。
足し合わせるべき要素 (つまり where の位置) を見つけると、状態の次元のうちいくつかが急激に変化している様子がわかります。
たしかに系列データに含まれているイベントを検知できるように学習ができているようです。
まとめ
個人的に RWA は LSTM よりもかなりシンプルでわかりやすく、直感的な発想をうまく実現できている気がします。
提案論文中では、もっとも単純な LSTM との比較しかおこなわれておらず、attention 付きの LSTM と比べたらどうなるのかといった問題や、LSTM でよくやられるように層を積み上げて multi-layer (stacked) にしたらどうなるのかといった点はまだわかりません。
(もっとも、attention モデルに関しては適用できる状況が限定されますし、RWA が attention の一般化のようになっているので比較はしないということかもしれませんが・・・)
今後もっと研究が進めば、もしかしたら LSTM を置き換えて RWA がデファクトスタンダードとして使われるようになるのではないかなと思っています。